נטגר גליון 1

---

דבר העורך

רון אהרוני

העיתון המתמטי הראשון לנוער יצא כנראה ב-$latex {1894}$ בהונגריה. קוראים לו $latex {Komal}$ והוא יוצא עד עצם היום הזה. דורות של מתמטיקאים הונגריים חונכו על דפי העיתון הזה, וקרוב לוודאי שהיה לזה חלק בכך שהונגריה הייתה לאורך כל המאה העשרים מעצמה מתמטית, והיא כזו עד עצם היום הזה. בארץ זכור לטוב "גליונות מתמטיקה", שיצא במכון וויצמן בעריכת פרופסור גיליס המנוח, ולאחריו "אתגר" שיצא בטכניון.

אנחנו מחדשים את המסורת, והפעם, ברוח הזמן, העיתון הוא ללא נייר. למי הוא מיועד? התשובה הפשוטה היא - למי שאוהב דברים כאלה (אברהם לינקולן השיב פעם לשאלה אם ספר מסוים הוא טוב, ב"זה ספר מצוין, למי שאוהב ספרים כאלה"). כלומר, זה לא חייב להיות נוער. העיתון מיועד לכל מי שמתעניין. זה שהעיתון מוגדר כ"עיתון לנוער" זה משום שנערים הם בדרך כלל הנלהבים ביותר.

אז מה יהיה לנו? כמו בכל עיתון מתמטי לנוער, יהיה מדור בעיות. נשמח למשוב מצידכם - קשות מדי? קלות מדי? יהיה גם מדור על ההיסטוריה של המתמטיקה, ולפעמים משהו על דרכי הוראת המתמטיקה. גם כאן נשמח למשוב - האם הייתם מעוניינים במאמר על נושא מתמטי מבית הספר התיכון, שלדעתכם אין מלמדים אותו היטב? יהיה גם מדור על דמויות במתמטיקה - במידת האפשר, בצורת ראיונות עם מתמטיקאים ידועים. בגיליון הראשון מופיע ראיון עם אחד המתמטיקאים הישראלים הבולטים, נוגה אלון (תודה נתונה לפרופ' צבי ציגלר על הפקת הראיון הזה). יהיה גם מדור של השערות פתוחות, לאלו מכם שרוצים לנסות את מזלם ואת כשרונם, או סתם לדעת מה מעניין מתמטיקאים בני ימינו. המאמר הראשון בסדרה הוא על השערה קומבינטורית, והוא נכתב על ידי דיקן הפקולטה למתמטיקה, פרופ' הולצמן.

וכמובן, אתם מוזמנים לתרום! כל מאמר או בעיה שיישלחו יידונו ברצינות על ידי המערכת.

זוהי הזדמנות להודות לעושים במלאכה: ד”ר יוסי כהן, הממונה על הפקת העיתון; אורי פרץ בונה האתר, ד”ר גדי אלכסנדרוביץ’, שיחד עם אורי מטפלים בכל הבעיות הטכניות המורכבות של עיתון אינטרנטי. אגב - הבלוג של גדי הוא שם דבר בקרב חובבי המתמטיקה בארץ. למי שאינו מכיר, הכתובת היא: $latex {http://www.gadial.net/}$.

רון אהרוני,
הפקולטה למתמטיקה, הטכניון

---

קסמה של המתמטיקה

נוגה אלון

כשהייתי בן 9, סיפרו לי הורי יום אחד שבפגישה עם ידידים בערב הקודם דירג כל אחד מהנוכחים רשימה בת עשרה איברים בסדר לינארי. הרשימה הספציפית אינה זכורה לי, אך לצורך הדיון הבה נניח שהמדובר היה בעשרת השירים בתחרות זמר כלשהי ששודרה ברדיו, וכל אדם רשם את הדירוג הסופי הצפוי לפי הערכתו, לאחר ששמע את השירים. בהמשך הערב, כשהתברר הדירוג הסופי לפי החלטת השופטים, בדק כל אחד מן הידידים את טיב הניחוש שלו לכל שיר ע"י חישוב הערך המוחלט של ההפרש בין מיקומו של השיר לפי הניחוש ומיקומו בהחלטת השופטים. הטיב הכולל של הניחוש של כל אחד מן הנוכחים נקבע כסכום עשרת הערכים המוחלטים של ההפרשים שחישב לשירים השונים, כאשר סכום קטן יותר מתאים כמובן לניחוש נכון יותר (או לפחות קרוב יותר לטעמם של השופטים). בסיום הערב ציין כל אחד מן הידידים את ערך הסכום שקיבל, והסכומים שהוזכרו (לצורך הדיון, אינני זוכר כמובן את המספרים המדויקים) היו 18, 20, 22, 17, 14 ו-36. אמי תהתה אם הערך 17 הוא אכן ערך אפשרי ; למרות שכסופרת ומתרגמת הייתה בעלת תחומי עניין רחוקים מן המדעים המדויקים, היא ניחנה באינטואיציה מתמטית בריאה, והייתה לה תחושה שערך הסכום חייב להיות זוגי. היא סיפרה לי את הסיפור ואני מצאתי אמנם הוכחה פשוטה לזוגיות הסכום (אני מניח שרוב הקוראים לא יתקשו למצוא הוכחה דומה).

 ככל ילד בן 9, היו לי מדי פעם ויכוחים עם הורי. ניסיתי לשכנע אותם, למשל, שמן הראוי לאפשר לי לנסוע לים לבדי, שכדאי לקנות לי אופניים או שרצוי לרשום אותי לשעורי פסנתר (וזמן קצר אח"כ, שחשוב להפסיק את שיעורי הפסנתר שלי באופן מיידי). אני זוכר שלאחר הדיון בזוגיות הציון, התרשמתי עמוקות מכך שגם ילד יכול לשכנע מבוגר אינטליגנטי בנכונותה של עובדה מתמטית בקלות רבה בהרבה מיכולתו לשכנע בדיון בנושאים אחרים, בדומה לאלה שהוזכרו לעיל. האמת המתמטית היא אובייקטיבית, וטיעון מתמטי נכון יכול להיות משכנע בוודאות מוחלטת בלי תלות ביכולת ההבעה של הטוען או בסמכותו המקצועית.

אינני חושב שהחלטתי להיות מתמטיקאי קשורה ישירות לסיפור שלמעלה ; למיטב זכרוני, כבר לפני גיל 9, התעניינתי בפתרון חידות מתמטיות והתלהבתי מהאתגר האינטלקטואלי שבנסיונות להתמודד עימן. ידעתי מגיל צעיר שברצוני להיות מתמטיקאי, הגם שכתלמיד בי"ס היה לי באופן טבעי מושג מעורפל למדי על אופיו ומהותו של המחקר המבוצע ע"י מתמטיקאי.

בתיכון למדתי בבי"ס הריאלי בחיפה, השתתפתי בחוגי העשרה מתמטית שארגן המורה שלי שם, מר יעקב קפלן, ונטלתי חלק בתחרויות נוער לפתרון בעיות מתמטיות שהתקיימו באותה עת בארץ. בסיום הלימודים נרשמתי ללימודי מתמטיקה במסגרת העתודה האקדמית של צה"ל, אך בשל מלחמת יום הכיפורים נדחו לימודיי, ושירתתי שנה בחיל השריון. אח"כ סיימתי תואר ראשון במתמטיקה בטכניון, ושירתתי ביחידת מחקר בצבא, שם שיתפתי פעולה עם כמה וכמה עמיתים שהפכו לימים לחוקרים מובילים במחלקות למתימטיקה, למדעי המחשב ולהנדסה באוניברסיטאות השונות בארץ. במהלך הלימודים הזדמן לי להיפגש עם פאול ארדש, מתמטיקאי הונגרי נודע שהיה נוהג לשוטט ברחבי העולם עם מזוודה חצי ריקה שהכילה את כל רכושו, להעלות השערות מתמטיות ולהתוות דרכים לפתרונן. שאלה ששמעתי מארדש הובילה לעבודת המאסטר שלי באוניברסיטת ת"א, אותה כתבתי בהנחייתו של פרופ' מיכה פרלס מן האוניברסיטה העברית, והפגישות והדיונים עם ארדש, תחילה כסטודנט בארץ ואח"כ כחוקר צעיר ב-MIT ובאוניברסיטת ת"א, השפיעו רבות על כיווני המחקר שלי והניבו במשך השנים מספר מאמרים משותפים.

 תחום המחקר שלי הוא קומבינטוריקה, העוסקת במחקר של מבנים מתמטיים סופיים, ושימושיה במדעי המחשב תוך התמקדות בשיטות הסתברותיות ואלגבריות. התחום קסם לי מגיל צעיר, בעיקר משום שהבעיות המרכזיות בו מנוסחות לעיתים קרובות בצורה פשוטה ובהירה, שאינה דורשת רקע רב, אך פתרונן דורש לעיתים קרובות שימוש בכלים מתוחכמים מתחומים מתמטיים שונים. התוצאה הבאה שאפשר לקרוא לה "משפט המחרוזת", מדגימה זאת היטב:

כל מחרוזת המכילה חרוזים מ-T צבעים שונים, באופן שמספר החרוזים בכל צבע מתחלק ב- K, אפשר לחתוך ב- $latex {(K-1)T}$ מקומות, ולחלק את האינטרוולים הנוצרים ל-K משפחות, שבכל אחת בדיוק אותו מספר חרוזים מכל צבע.

הניסוח כאן אלמנטרי ופשוט, אך ההוכחה הידועה היחידה משתמשת בשיטות טופולוגיות מתוחכמות.

  לקומבינטוריקה שימושים רבים בתחומים שונים, לרבות תורת האינפורמציה, מדעי המחשב התיאורטיים, תורת המספרים וגיאומטריה, והיא תופסת מקום מרכזי יותר ויותר במתמטיקה המודרנית, בה ההתמקדות בשיטות קונסטרוקטיביות ובהיבטים כמותיים משמעותית בהרבה משהייתה בעבר. בעידן המודרני ברור לכל שלמתמטיקה ישנו תפקיד חשוב מאין כמוהו בפיתוח המדע והטכנולוגיה. עובדה פחות ידועה, אולי, היא יופייה של המתמטיקה כמדע העומד בפני עצמו. כפי שכתב המתמטיקאי הבריטי הנודע,

G. H. Hardy: "ייתכן שקשה מאוד להגדיר יופי מתמטי, אך עובדה דומה נכונה גם לגבי יופי בכל תחום אחר. קרוב לוודאי שאיננו יודעים למה בדיוק כוונתנו כשאנו קובעים שיצירה מוסיקלית היא יפה, אך זה איננו מונע מאיתנו לזהות זאת כשאנו שומעים אותה".

 יופייה של המתמטיקה מתבטא בקשרים בלתי צפויים בין תחומים שונים, בהוכחות קצרות ואלגנטיות, בוודאות המוחלטת הנובעת מנכונותה של הוכחה ובאתגר האינטלקטואלי במציאתה. אחת התכונות החשובות ביותר של מתמטיקאי היא היכולת לזהות יופי מתימטי, והיכולת להמשיך ולהתלהב מיופי זה לאורך שנים של מחקר.

נוגה אלון הוא פרופסור למתימטיקה ולמדעי המחשב באוניברסיטת תל-אביב, ובעל מינוי מיוחד כפרופסור אורח במכון ללימודים מתקדמים בפרינסטון. פירסם למעלה מ-400 מאמרים, רובם בקומבינטוריקה ובמדעי המחשב התיאורטיים. הוא חבר האקדמיה הישראלית למדעים, חבר האקדמיה האירופאית למדעים, וזכה בפרסים רבים בארץ ובעולם, לרבות פרס ארדש, פרס פהר, פרס Polya, פרס ברונו, פרס לנדאו, פרס Gödel ופרס ישראל.

---

בניות בסרגל ומחוגה

גדי אלכסנדרוביץ

כשאומרים לנו “אי אפשר לרבע את המעגל” מתכוונים לבעיה שאין לה פתרון. אבל מאיפה הביטוי הזה בכלל הגיע? רובנו יודעים שהוא הגיע אי שם ממשהו במתמטיקה, אבל למה הוא הפך למילה נרדפת למשהו בלתי אפשרי? מה כל כך קשה בלקחת מעגל ולהפוך אותו לריבוע? פשוט ניקח את ה”חוט” שמרכיב את המעגל וניישר קצת את הקצוות שלו, לא?

ובכן, זה באמת לא עד כדי כך פשוט, אחרת לא היה מדובר בבעיה שראשיתה עוד בימי יוון העתיקה, ובמשך קרוב לאלפיים שנה היא עמדה ללא פתרון עד להכרעה הסופית בעניינה בשלהי המאה ה-19, שבה הוכח כי הבעיה היא אכן בלתי פתירה (מה שלא מונע עד עצם היום הזה מאנשים לטעון שהם פתרו אותה בקלי קלות - לרוב מכיוון שהם בכלל לא הבינו מה הבעיה אומרת).

אז מה הבעיה אומרת? בפשטות, השאלה שמציבה הבעיה היא האם ניתן, בהינתן מעגל נתון, ניתן לבנות באמצעות סרגל ומחוגה ריבוע ששטחו שווה לשטח המעגל. שני הכלים הללו - סרגל ומחוגה - הם לב העניין. מחוגה היא הכלי שאנחנו מכירים מבית הספר - כלי בעל שתי “רגליים” שאפשר להניח על דף נייר ולסובב אותו כך שיצייר מעגל שאחת הרגליים היא במרכזו והרגל השניה היא עליו. “סרגל” הוא גם הכלי שאנחנו מכירים מבית הספר - כלי שמאפשר לצייר קווים ישרים - אבל בלי סימוני האורך שעליו. במילים אחרות, לא סרגל שמאפשר לנו לבצע מדידה אלא רק לצייר קווים ישרים. באנגלית ההבחנה בין שני הכלים הללו יותר חדה - סרגל שמאפשר לנו למדוד נקרא Ruler, וסרגל שמאפשר רק לצייר קווים ישרים נקרא Straightedge.

שני הכלים הללו הם פשוטים למדי לייצור, ושימושיים במידה מפתיעה, מה שמסביר את הפופולריות שלהם ביוון העתיקה, שהגיאומטריה הייתה התחום המתמטי המרכזי בה. הרעיון הבסיסי בכלים הללו הוא שה”עולם” שלנו מורכב משלושה אובייקטים: נקודות, קווים ישרים ומעגלים. כללי המשחק הם כאלו: בהינתן שתי נקודות, אפשר למתוח קו ישר (שיכול להיות ארוך בצורה בלתי מוגבלת לכל אחד משני כיווניו) שעובר דרך שתי הנקודות הללו; ובהינתן שתי נקודות אפשר לצייר מעגל שמרכזו בנקודה אחת והוא עובר דרך הנקודה האחרת; ובהינתן ששני ישרים, או שני מעגלים, או מעגל וישר נחתכים, זה יוצר נקודה חדשה בנקודת החיתוך שאחר כך אפשר להשתמש בה בהמשך הבניות שלנו.

על פניו זה נשמע שאנחנו מאוד מוגבלים עם הכלים הללו ולא יכולים לעשות יותר מדי, אבל מסתבר שאפשר לעשות הרבה מאוד דברים, וזה בהחלט מפתיע. למשל, קל מאוד להעביר אנך לישר נתון: לוקחים שתי נקודות על הישר ומעבירים שני מעגלים, כך שכל אחד מהם עובר דרך אחת הנקודות ומרכזו בנקודה השניה. שני המעגלים הללו עומדים להיחתך בשתי נקודות; נעביר קו ישר דרך שתי הנקודות הללו והופס - קיבלנו אנך לישר המקורי. הנה איך כל זה נראה בציור:

למה זה עובד? ובכן, הנה דרך אחת לראות את זה: נתבונן בקווים המחברים את הנקודות שעל הישר שממנו התחלנו, עם נקודות החיתוך של המעגלים. כל קו כזה הוא רדיוס של אחד מהמעגלים, ולשני המעגלים אותו הרדיוס. מסקנה: ארבעת הקווים הללו הם מאותו האורך, ולכן ביחד הם יוצרים מעוין. אחד מהאלכסונים של המעוין הוא הישר שממנו התחלנו, והשני הוא הישר שעובר דרך שתי נקודות החיתוך של המעגלים; כעת נשתמש במשפט ידוע מגיאומטריה שקובע שהאלכסונים במעוין מאונכים זה לזה, וסיימנו.

וזה רק קצה הקרחון של מה שאפשר לעשות. המשתמש Aldoaldoz בויקיפדיה האנגלית יצר כמה סרטונים נפלאים שמציגים בניות אפשריות. למשל, בניה של ריבוע (כאן האתגר גדול יותר מסתם לבנות ישר מאונך; צריך לבנות קווים מאונכים זה לזה שכולם באותו האורך):

והנה תעלול אחר - אנחנו מתחילים עם קטע, ומחלקים אותו לשלושה חלקים - דהיינו, אנחנו “גוזרים” ממנו קטע שאורכו הוא שליש מאורך הקטע המקורי:

אם אתם רוצים להשתשע במשחקים הללו בעצמכם, תוכנה נוחה מאוד לשימוש שמאפשרת לבצע בדיוק את הדברים הללו נקראת Geogebra וזמינה בחינם כאן.

היוונים היו טובים מאוד במשחקים הללו, אבל היו מספר בעיות בניה שלא עלה בידיהם להתגבר עליהן. מביניהן שלוש בעיות היו מפורסמות במיוחד: בעיית החלוקה לשלוש של זווית; בעיית הכפלת הקוביה; ובעיית ריבוע העיגול. שלושתן קלות למדי לניסוח: הראשונה מבקשת לבנות, בהינתן זווית קיימת, זווית חדשה הקטנה ממנה פי 3 (“זווית” בעולם שלנו נתונה על ידי שני ישרים בעלי נקודת חיתוך משותפת; אני מקווה שמבחינה אינטואיטיבית הרעיון ברור). הבעיה השניה מבקשת, בהינתן קוביה קיימת, לבנות קוביה חדשה בעלת נפח גדול פי 2; והבעיה השלישית מבקשת, בהינתן מעגל נתון, לבנות ריבוע ששטחו כשטח העיגול.

שלוש הבעיות הללו נותרו בלתי פתורות במשך אלפי שנים, עד אשר במהלך המאה ה-19 פותחו שיטות מתמטיות שהציעו דרך התבוננות חדשה על הבעיות הללו ובסופו של דבר הוכיחו שאין להן פתרון - בעזרת סרגל ומחוגה לא ניתן לבצע את הבניות הללו. מהי דרך ההתבוננות הזו? ראשית, לחשוב על שלוש הבעיות הללו בתור בעיות בניה של מספרים; ושנית, שימוש בטכניקות אלגבריות (מהסוג שכלל לא היה מוכר ליוונים) כדי לקבוע אילו מספרים ניתן “לבנות” ואילו לא ניתן. חשוב לי להדגיש כבר בשלב זה שכאשר אני אומר טכניקות “אלגבריות” איני מתכוון לאלגברה התיכונית, שכוללת בעיקר פתרון משוואות; הכוונה לתורה עמוקה ומעניינת משמעותית יותר.

למה אני מתכוון כשאני אומר “בניה של מספרים”? הכוונה לבניה של קטעים שהאורך שלהם שווה למספר נתון. הרעיון הוא שאנחנו מתחילים את משחקי הבניה שלנו כאשר כל מה שיש לנו הוא קטע יחיד שקצותיו בשתי נקודות נתונות; לאורך של הקטע הזה נקרא “1”. עכשיו, אם אנחנו מצליחים לבנות קטע מאורך כפול, נקרא לו “2”; אם אנחנו מצליחים לבנות קטע שאורכו חצי מאורך הקטע המקורי נקרא לו “$latex \frac{1}{2}$”, וכן הלאה.

עכשיו אפשר להסביר למה אפשר לתאר את שלוש הבעיות שלעיל בתור בעיות בניה של מספרים. ראשית, הכפלת הקוביה. קוביה היא אמנם אובייקט תלת-ממדי, אבל מספיק לדבר על בניה של גודל הצלע שלה (בקוביה כל הצלעות זהות בגודלן). נפח של תיבה באופן כללי הוא מכפלת גובה התיבה באורך וברוחב שלה; במקרה של קוביה עם אורך צלע $latex a$, נפח הקוביה הוא $latex a^{3}$.

כעת, נניח שהתחלנו עם קוביה שאורך הצלע שלה הוא 1, ולכן נפחה הכולל הוא גם כן 1; אנחנו רוצים לבנות קוביה עם נפח 2. מתבקש לנסות ולהסתכל פשוט על הקוביה שאורך צלעה הוא 2, אבל נפח הקוביה הזו הוא $latex 2\cdot2\cdot2=8$ - גדול הרבה יותר ממה שאנו צריכים. אורך הצלע שאנו רוצים לבנות הוא $latex \sqrt[3]{2}$ - השורש השלישי של 2, שהוא בערך $latex 1.25992\dots$. הנה לנו בעיה ראשונה שתורגמה ל”בניית מספר”.

בעיית ריבוע המעגל דומה: נניח שהתחלנו עם מעגל שרדיוסו 1. אנחנו יודעים שבאופן כללי שטח של מעגל מרדיוס $latex R$ הוא $latex \pi R^{2}$, כאשר $latex \pi$ (האות היוונית פאי) הוא סימון ליחס הקבוע בין היקף מעגל וקוטרו, ושווה בערך ל-$latex 3.14\dots$ (זהו שעשוע פופולרי לזכור כמה שיותר ספרות של $latex \pi$ לאחר הנקודה שרק אפשר - אני מאוד גרוע בו). אם המעגל שלנו הוא מרדיוס 1, הרי ששטחו הוא $latex \pi$ ולכן אנו רוצים לבנות ריבוע שאורך צלעו הוא $latex \sqrt{\pi}$. שוב, הגענו לבניה של מספר.

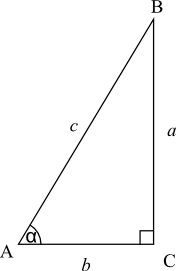
הבעיה השלישית נראית מנותקת לגמרי ממספרים - איך נעבור מזווית לאורך של צלע? כאן נחלצת לעזרתנו הטריגונומטריה. הדרך הפשוטה ביותר להסביר זאת היא על ידי התבוננות באיור הבא:

במשולש ישר זווית, הצלע שנמצאת מול הזווית בת ה-90 מעלות נקראת היתר של המשולש. שתי הצלעות האחרות נקראת “אנכים”. כעת, הפונקציות המתמטיות של סינוס וקוסינוס ניתנות להגדרה עבור זוויות במשולש באופן הבא: סינוס של זווית במשולש (שאינה הזווית בת 90 המעלות) הוא היחס בין אורך האנך שנמצא מול הזווית (כלומר, לא נוגע בה) ובין אורך היתר, ואילו קוסינוס הזווית הוא היחס בין אורך האנך שנמצא ליד הזווית ובין אורך היתר. כלומר, עבור המשולש שבאיור, $latex \sin\alpha=\frac{a}{c}$ ו-$latex \cos\alpha=\frac{b}{c}$.

כעת, אם אנחנו רוצים לבנות את הזווית $latex \alpha$, אפשר לעשות זאת בקלי קלות על ידי בניית קטעים באורכים מסויימים: ראשית נבנה קטע שאורכו בדיוק $latex \sin\alpha$; כעת נבנה אליו אנך באחד מקצותיו שאורכו הוא $latex \cos\alpha$; לבסוף, נחבר את שתי נקודות הקצה של הקטעים שבנינו ונקבל יתר במשולש ישר זווית שאורכו בדיוק 1, והזווית שהוא יוצר עם הקטע האופקי היא בדיוק $latex \alpha$. לכן בעיית הבניה של הזווית $latex \alpha$ שקולה לבעיית הבניה של המספרים $latex \sin\alpha,\cos\alpha$.

אם כך, הניסוח של הבעיות שלנו עובר מניסוח גיאומטרי לניסוח אלגברי - נשאלת השאלה אילו מספרים אפשר לבנות, כאשר כללי הבניה שלנו נובעים בצורה כלשהי ממה שניתן לעשות עם סרגל ומחוגה. המספר הבסיסי שנתון לנו בתחילת ה”משחק” הוא 1, ואנחנו רוצים לבנות כל מספר אחר מתוך 1 והפעולות שמותר לנו לבצע. מה שעוד נותר להסביר הוא אילו פעולות אלגבריות ניתן לבצע באמצעות הכלים הגיאומטריים שלנו?

התשובה היא פשוטה למדי: בעזרת סרגל ומחוגה ניתן לבצע את ארבע פעולות החשבון הבסיסיות - חיבור, חיסור, כפל וחילוק. לכן אפשר, למשל, לבנות את $latex \frac{3}{4}$: נבנה את 3 בתור $latex 1+1+1$, נבנה את $latex 4$ בתור $latex 3+1$, ולבסוף נבנה את $latex \frac{3}{4}$. בנוסף לארבע פעולות החשבון, יש עוד דבר אחד שניתן לעשות - הוצאת שורש ריבועי. כלומר, את $latex \sqrt{2}$ אפשר לבנות, למשל. במאמר הבא נראה בדיוק איך מבצעים את כל הפעולות הללו באמעות סרגל ומחוגה, אך אני ממליץ לכם לנסות ולגלות זאת באופן עצמאי - גם אם לא תצליחו, המשחק הזה יאפשר לכם להבין טוב יותר את האתגרים והשעשועים שיש בבניות בסרגל ומחוגה.

במאמר הבא גם נסביר מדוע חמש הפעולות הללו יכולות לתת את כל המספרים הניתנים לבניה, ומדוע מכך נובע ששלוש בעיות הבניה שהצגתי אינן פתירות.

---

מתמטיקה, שירה וקסמים

רון אהרוני

מתמטיקה היא דבר מועיל מאין כמותו. כל המדע המודרני מבוסס עליה. ובכל זאת, אם תשאלו מתמטיקאי מה מושך אותו לעסוק במקצועו, תקבלו תשובה אחידה: יופי. “אין מקום תחת השמיים למתמטיקה מכוערת”, אמר המתמטיקאי האנגלי הרדי.

במיוחד, יש המשווים את היופי של המתמטיקה ליופי של השירה. “מתמטיקאי שאינו גם קצת משורר איננו מתמטיקאי מושלם”, אמר המתמטיקאי הגרמני קרל ווירשרטאס ($latex {1897 - 1815}$). “אוקלידס היה היחיד שראה את היופי בעירומו” העידה המשוררת האמריקנית עדנה וינסנט מיליי. כיצד ייתכן הדבר? המתמטיקה עוסקת במציאת סדר בעולם החומרי. שירה עוסקת ברגשות. מה הקשר בין השתיים?

במאמר הזה אגע בשאלה הזאת על קצה המזלג. הקטעים הבאים לקוחים מספר שהקדשתי לנושא, “מתמטיקה, שירה ויופי”, שפורסם בהוצאת הקיבוץ המאוחד ב-$latex {2008}$.

1. כייסים הפוכים

את התשובה לשאלה מהו המשותף בין היופי בשירה ובמתמטיקה אפשר לסכם במילה אחת: קסמים.

“קסם” פירושו שאינך יכול לעקוב אחר המתרחש. הדברים קורים מהר מדי. איננו מבינים עד הסוף. כאשר מופיע פתרון לא צפוי לבעיה מתמטית, כאילו “משום מקום”, אנחנו חשים יופי, משום שאיננו מבינים לגמרי. הקרקע נשמטה תחת רגלינו. גם בשירה זה קורה, אלא ששם זו אינה תופעת לוואי. זוהי המטרה. השיר חותר לכך שנקלוט את המסר בלי לדעת שקלטנו. שיר הוא כייס, שבמקום לגנוב משהו, מכניס לנו משהו לכיס בלי שנרגיש. השיר רוצה שנקלוט משהו מבלי משים.

2. למה שירים הם (לפעמים) בחרוזים?

עד לפני כמאה שנים רוב השירה הייתה בחריזה, וגם כיום שירה כתובה במשקל, כלומר קצב הטעמות קבוע. האם שאלתם את עצמכם אי פעם מדוע?

התשובה לא צפויה - זה נעשה להסחת דעת. תשומת הלב של השומע מופנה לצד החיצוני - לתבנית החוזרת של הצלילים. זה נעים, וזה מרדים, כמו נענוע של ערישה. וכשתשומת הלב מופנית לצורה החיצונית, קל יותר להעביר את המסרים. הכייס יכול לעשות את עבודתו באין מפריע.

החריזה והמשקל אינן התחבולות היחידות. יש עוד רבות, ועל כמה מהן נספר כאן. אבל לפני כן, אדגים את עניין ה”קסמים” במתמטיקה.

3. כמה משחקים יש בטורניר גביע

הנה דוגמה לפתרון יפה לבעיה מתמטית. משהו נראה כבלגן, ואז מופיע סדר בלתי צפוי.

“טורניר גביע” הוא תחרות שבה השחקנים מתחלקים לזוגות, כל זוג עורך משחק, והמנצח עולה לשלב הבא. שאלה: כמה משחקים ייערכו בטורניר שבו משתתפים $latex {16}$ שחקנים? בואו נעקוב אחר הסיבובים. בסיבוב הראשון יסתדרו $latex {16}$ השחקנים ב-8 זוגות. 8 משחקים יתקיימו, ו-8 שחקנים יעלו לשלב הבא. 8 השחקנים שעלו לסיבוב השני יסתדרו ב-4 זוגות, וישחקו 4 משחקים. בסיבוב השלישי יהיו 2 משחקים, וברביעי, שבו נקבע מחזיק הגביע, 1. יחד: $latex {15}$. $latex {16}$ הוא חֶזְקה של 2 - הוא $latex {2^4}$. משום כך בכל סיבוב אפשר היה לסדר את כל השחקנים בזוגות. אבל אפשר לקיים טורניר גם עם מספר שחקנים שאינו חֶזקה של 2. במקרה זה, יש סיבובים שבהם מספר השחקנים אינו זוגי, ואי אפשר לחלק את כולם לזוגות. כאשר דבר זה קורה, מתחלקים השחקנים לזוגות פרט לשחקן אחד, והשחקן העודף עולה לסיבוב הבא בלי לשחק. כמה משחקים ייערכו אז?

בואו ואֲלמֵד אתכם את סודם העיקרי של המתמטיקאים, סוד שהם מחלקים עם המשוררים ואשר נחזור אליו שוב ושוב: הם חושבים בדוגמאות. המתמטיקה אומנם מופשטת, אבל אל ההפשטות מגיעים מדוגמאות. המתמטיקאים גם יודעים שככל שהדוגמה פשוטה כן ייטב. אין דבר כזה, “דוגמה פשוטה מדי”. ובכן, הדוגמה הפשוטה ביותר היא של שחקן אחד. במקרה זה, כמובן, אין כלל מִשחקים והשחקן היחיד מוכרז כמנצח. כשיש שחקן אחד מספר המשחקים הוא אפוא 0. בדוגמה הבאה בתור בפשטותה, תחרות עם 2 שחקנים, יש משחק אחד. כשיש 3 שחקנים מתקיימים שני משחקים: משחק בין זוג, ואחריו עוד משחק בין המנצח בסיבוב הראשון ובין השחקן שהמתין בצד. נתקדם מעט וניקח כדוגמה טורניר של $latex {10}$ שחקנים. בסיבוב הראשון יתקיימו 5 משחקים, ו-5 שחקנים יעלו לשלב הבא. בסיבוב השני ישחקו 2 זוגות, ושחקן אחד יעלה ללא משחק. בסיבוב זה יתקיימו אפוא 2 משחקים, ויעלו 3 שחקנים. בסיבוב הבא ישחקו 2 מתוך ה-3 משחק אחד, ויעלו שני שחקנים - המנצח במשחק, והשחקן שלא שיחק. בסיבוב האחרון ייערך משחק אחד בין אותם שני שחקנים.

בסיבוב הראשון נערכו 5 משחקים, בשני 2, בשלישי 1 וברביעי 1.

יחד: $latex {9}$. זה לא היה קשה במיוחד, אבל במקרה של $latex {1000}$ שחקנים החישוב יהיה כבר קשה ומייגע. האם יש דרך קלה יותר? שימו לב שבכל המקרים האלה מספר המשחקים היה שווה למספר השחקנים, פחות 1. יש לשער שזה אינו מקרה, כלומר שיש לכך סיבה. מתבקש לשער שהדבר נכון תמיד: מספר המשחקים תמיד קטן באחד ממספר השחקנים. השערה טובה היא שלב מכריע בכל תגלית, אבל היא דורשת הוכחה. במקרה זה, כדי להבין את הסיבה לנכונותה של ההשערה צריך לראות את התמונה מזווית אחרת, כלומר לבצע התקה: מהתבוננות במנצחים להתבוננות במפסידים. לצורך הדוגמה נתבונן במקרה שבו משתתפים בטורניר $latex {1000}$ שחקנים. כל אחד מ-$latex {999}$ השחקנים שלא זכו בגביע הפסיד בדיוק פעם אחת: היה בדיוק משחק אחד שבו “הועף” מן הטורניר. כיוון שבכל משחק יש מפסיד אחד בדיוק, כדי ש-$latex {999}$ שחקנים יפסידו, נחוצים $latex {999}$ משחקים! ללא ספק, הרבה יותר פשוט.

כאשר נמצא מפתח לפתרון בעיה, בדרך כלל הוא פותח דלתות רבות נוספות. הוא מספק תשובה לא רק לשאלה המקורית, אלא גם לשאלות כלליות יותר. במקרה זה, אפשר למשל להכליל את חוקי התחרות: בכל שלב משחקים כמה זוגות (לא חשוב כמה, העיקר שלפחות זוג אחד משחק), ולשלב הבא עולים המנצחים במשחקים אלה, וכן כל השחקנים שלא שיחקו. לא מאוד הוגן, משום שלחלק מן השחקנים יש חיים יותר קלים מלאחרים, אבל לגיטימי, לפחות מבחינה מתמטית. כמה משחקים נערכים במקרה זה? ובכן, גם בנוסח הזה מפסיד כל שחקן, פרט לזוכה בטורניר, בדיוק במשחק אחד, ועל כן מתקבלת אותה תשובה: מספר המשחקים הוא כמספר היוצאים מן התחרות. כלומר, כמספר השחקנים פחות 1.

באבחת חשיבה אחת נפתרה בעיה שנראתה ממבט ראשון מורכבת ומסובכת. כבמעין קסם הופיע רעיון חדש, של הסתכלות במפסידים במקום במנצחים, והכול התבהר. תחושת הקסם נובעת מכך שהכול קורה מהר מדי, ואיננו מצליחים לעקוב עד תום אחרי המפנה שהתרחש.

4. שתי תחבולות שיריות

התחבולה המוכרת ביותר של השירה, והמזוהה איתה יותר מכל תחבולה אחרת, היא המטפורה. מטפורה היא “השאלה”. לוקחים תבנית מוכרת ממקום אחד, ומשתמשים בה במקום שני. למשל, “ללכת על קרח דק”, “להכות על הברזל בעודו חם”. בשפת היומיום יש לשימוש במטפורות שני יתרונות: בדרך כלל משתמשים בתמונות, ותמונות מבינים יותר טוב מאשר מילם מופשטות. שנית, אפשר להעביר תבנית שלמה במילים קצרות. במקום לבנות בניין חדש, מעבירים בניין קיים ממקום אחר. זה יכול לחסוך הרבה עבודה.

בשירה יש לשימוש במטפורות מטרה נוספת: המטפורה היא כמו קוסם שמפנה את תשומת ליבנו למה שהוא עושה ביד שמאל, כשאת התעלול הוא מבצע ביד ימין. אנחנו חושבים על המדמה, ואילו את המדומה אנחנו קולטים בלי משים.

כדוגמה אקח את מה שהוא קרוב לוודאי השיר הכי מפורסם בעולם. לא - אינני מתכוון ל”אל הציפור”, וגם לא ל”הכניסיני תחת כנפך”. השיר שזכה להכי הרבה תרגומים, ושידוע יותר מכל שיר אחר גם מחוץ לשפת המקור שלו, הוא “שיר הלילה של הנודד” של המשורר הגרמני יוהן וולפגנג גתה ($latex {1749}$ - $latex {1832}$).

השיר הזה נכתב בתחילת תקופת הרומנטיקה, שחרתה על דגלה את האינדיבידואל. בספרות הרומנטית הופיעו דמויות סובלות, הנאבקות על האמת הפנימית שלהן. הגיבורים יצאו למסעות של גילוי עצמי - את החיפוש העצמי באמצעות נדודים בעולם לא המציאו התרמילאים של ימינו. גיבור “שיר הלילה של הנודד” הוא הלך, כנראה למוד אכזבות, או אף אוהב נכזב. השיר מתחזה בתחילתו לשיר טבע. עד השורה האחרונה, שנותנת לכל משמעות חדשה. מתברר בה שכל מה שרואים בחוץ מייצג למעשה את מה שקורה בפנים.

למעשה, זהו מהלך שמתחולל כמעט בכל שיר. כל שיר מתחיל בחוץ ומסיים בפנים, בתוך נפשו של הגיבור.

מֵעַל כָּל פְּסָגוֹת

דְּמָמָה,

בְּצַמְּרוֹת הָעֵצִים

לֹא תִּשְׁמַע

אִוְשַׁת רוּחַ

צִפֳּרִים שׁוֹתְקוֹת בַּסְּבַךְ

חַכֵּה, עוֹד מְעַט

גַּם אַתָּה תָּנוּחַ.

השיר מורכב משני חלקים. בשש השורות הראשונות מצוירת תמונה פסטורלית כביכול: פסגות הרים, צמרות עצים וציפורים. למעשה, זוהי תמונה מאיימת, משום שהכול שקט ודומם. לתחושת אי השקט מוסיף המשקל, המשתנה משורה לשורה, ונדמה שהוא משקף את הערעור הפנימי של הגיבור. אותו אפקט יש לחריזה, שאינה קבועה. לפעמים מתחרזת שורה עם השורה שאחריה, לפעמים מתחרזות שתי שורות שמופרדות על ידי שורה אחת, ובין ה”רוח” וה”תנוח” מפרידות שתי שורות. ולבסוף, בשתי השורות האחרונות, מתברר הכול: השקט המאיים אינו אלא שיקוף רצונו של הנודד למות. המוות מופיע בדרך סמלית, כמנוחה.

5. תפניות פתאומיות

השיר הזה משתמש בתחבולה נוספת: התפנית הפתאומית שמתחוללת בשורה האחרונה.

התחבולה הזאת, של שורה שבה כל המשמעות משתנה, מופיעה בשירים רבים. חוקר הספרות הישראלי מנחם פרי קרא לשירים כאלה “שירים מתהפכים”. הוא טען שיש הרבה יותר שירים מתהפכים מאשר נראה על פני השטח. למשל, לדעתו כרבע משירי ביאליק הם שירים מתהפכים.

מהו הקסם בזאת? כיצד גורמת התפנית הפתאומית לשומע לדעת משהו בלי לדעת עד תום? הסוד הוא בכך שכאשר התפנית מתרחשת, צריך להבין הרבה מאוד בבת אחת. פתאום נחוץ לפרש את כל מה שקרה עד כה בדרך אחרת. וכשזה קורה, אי אפשר להבין הכל, לפחות לא במודע. יותר מדי אינפורמציה אמורה להיקלט בבת אחת.

ממש כמו בפתרון יפה של בעיה מתמטית, שבו איננו יכולים להבין הכל כל כך מהר.

6. המקרה המוזר של הנמלים על המוט

רַק עַל עַצְמִי לְסַפֵּר יָדַעְתִּי

צַר עוֹלָמִי כְּעוֹלַם נְמָלָה.

(“רק על עצמי”, רחל (בלובשטיין), $latex {1890 - 1931}$)

בפתרון יפה של בעיה מתמטית קורה בדיוק אותו דבר שמתרחש בשירים מתהפכים: רעיון חדש מגיח כאילו משום מקום, ומבהיר את התמונה. אלא שהרעיון כל כך לא צפוי, שאיננו קולטים אותו במפורש ועד תומו. גם כשנפגוש בו שוב עדיין לא נקלוט את מלוא עומקו, ולכן הוא יכול להמשיך ולעורר בנו תחושת יופי. ממש כפי שאפשר ליהנות שוב ושוב משמיעה של סימפוניה של מוצרט - גם בפעם המאה איננו יכולים לפענח במפורש את כל הסדר שבה.

הנה עוד דוגמה מסוג זה. על מוט באורך מטר אחד נמצאות נמלים במספר כלשהו. הנמלים נעות - חלקן ימינה, חלקן שמאלה, אבל כולן באותה מהירות: בדיוק מטר אחד בדקה. המוט צר, כרוחב נמלה אחת, וכאשר שתי נמלים נפגשות אין הן יכולות להמשיך בדרכן. במקום זה הן מתנהגות כמו כדורי ביליארד שהתנגשו, כלומר כל אחת מהן הופכת את כיוונה וממשיכה בכיוון ההפוך, באותה מהירות.

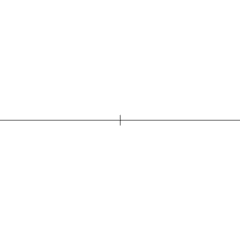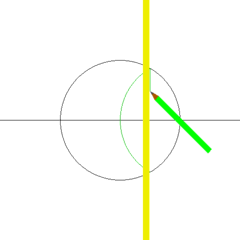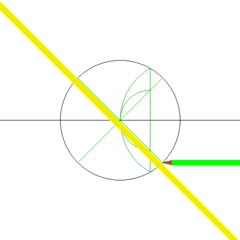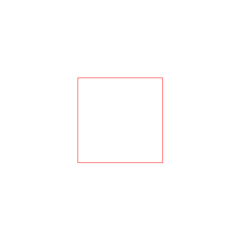
כששתי נמלים נפגשות (איור שמאלי) הן הופכות כיוון (איור ימני)

מדי פעם גם מגיעה נמלה לקצה המוט, ואז היא נופלת ונעלמת לבלי שוב. שאלה: האם בסופו של דבר ייפלו כל הנמלים מן המוט? ואם כן, תוך כמה זמן?

ממבט ראשון, נראה שהדבר תלוי במצב ההתחלתי, כלומר במספר הנמלים על המוט ובמערך שלהן. אם יש הרבה נמלים, נראה שאם בכלל ייפלו כולן, זה עלול לקחת זמן רב. איך אפשר לבחון זאת? סודם הראשון של המתמטיקאים הוא הסתכלות בדוגמאות. כל חשיבה מתמטית מתנהלת כמשחק פינג-פונג מעודן בין דוגמאות והפשטות. ההבדל בין החבטות בכיוון המופשט והחבטות בכיוון הדוגמאות הוא שאת הדוגמאות אפשר לזַמֵן בצורה מודעת, בעוד שתהליך ההפשטה מתרחש ללא שליטה מודעת. משום כך נחוץ לפתוח בדוגמאות. כמובן, סיבה נוספת לכך היא שהדוגמאות הן חומר הגלם להפשטות. ובכן, הדוגמה הפשוטה ביותר היא זו של נמלה אחת. אם הנמלה נמצאת בקצה אחד של המוט והולכת לכיוון הקצה השני, היא תיפול תוך דקה. בכל מקרה אחר היא תיפול תוך פחות מדקה. אבל לא נגענו כאן עדיין במהות הבעיה משום שבמקרה זה לא היו התנגשויות. נתבונן אפוא בשתי נמלים, ונתחיל במקרה שבו, כך נדמה לפחות, ייקח להן זמן רב ליפול: שתיהן נמצאות בקצוות מנוגדים והולכות זו בכיוונה של זו.

כעבור חצי דקה הן תיפגשנה באמצע המוט, תהפוכנה כיוון, וכעבור עוד חצי דקה הן תיפולנה כל אחת באותו קצה שממנה יצאה. אם כך, שתיהן תיפולנה אחרי דקה אחת בדיוק. הנה דוגמה קצת יותר מסובכת: נמלה א’ נמצאת בקצה הימני, נמלה ב’ נמצאת בדיוק באמצע המוט, והן הולכות זו לקראת זו.

פגישתן תהיה במרחק רבע מטר מן הקצה הימני, ואחריה תלך נמלה א’ עוד רבע מטר ימינה, עד שתיפול מן הקצה הימני, ואילו נמלה ב’, שכבר הלכה רבע מטר, תלך שמאלה עוד שלושת רבעי המטר עד שתיפול בצד השמאלי. בסך הכול תעבור נמלה ב’ מטר אחד, ומאחר שהיא הולכת מטר בדקה, הדבר ייקח לה דקה. זה כבר מתחיל לעורר חשד. בכל הדוגמאות שבדקנו עד כה כל הנמלים נפלו מן המוט תוך דקה. אבל ייתכן שעלינו לעלות בדרגת הסיבוך ולהתבונן בשלוש נמלים. ניקח למשל מקרה שבו נמלה א’ נמצאת בקצה הימני והולכת שמאלה; נמלה ב’ נמצאת בקצה השמאלי והולכת ימינה; נמלה ג’ נמצאת בדיוק באמצע והולכת ימינה.

לאחר רבע דקה תיפגשנה א’ ו-ג’, ותהפוכנה את כיוון הליכתן. ברגע הפגישה של א’ ו-ג’ נמצאת ג’ במרחק שלושת רבעי המטר מצד שמאל, ואילו ב’ נמצאת במרחק רבע מטר מצד שמאל. הנה כך:

לאחר שתהפוך את כיוונה, א’ תיפול עד מהרה בקצה הימני. נמלים ב’ ו-ג’ הולכות זו מול זו ולכן תיפגשנה באמצע המוט. עד אז הלכה כל אחת מהן חצי דקה. כשהן נפגשות הן משנות כיוון, ותוך חצי דקה נוספת תיפולנה שתיהן. שוב, דקה! תוך דקה בדיוק לא תישאר אף נמלה על המוט! מוזר למדי. בכל המקרים נפלו כל הנמלים תוך דקה. האם יש כאן חוק כללי? האם הדבר נכון תמיד? התשובה היא “כן”, וההוכחה אינה מסובכת, אבל היא דורשת הארה. כלומר, תובנה שהופכת באחת את הדברים לפשוטים בתכלית. למרבה המוזרות, ההארה אינה מוסיפה אינפורמציה, אלא דווקא להפך, מתעלמת מאינפורמציה. היא מתעלמת מזהותן של הנמלים. אם לא אכפת לנו מי הן הנמלים, מה קורה ברגע הפגישה של שתי נמלים? ובכן, למעשה לא קורה דבר. לפני הפגישה אחת הנמלים הלכה שמאלה והשנייה ימינה; אחרי הפגישה קורה בדיוק אותו דבר - גם אז נמלה אחת הולכת שמאלה והאחרת ימינה, באותן מהירויות. והרי איזו נמלה הולכת שמאלה ואיזו ימינה כלל אינו משנה לצורכי הבעיה! המסקנה היא שאפשר להתעלם כליל מן הפגישות. מטרתן רק לבלבל. השאלה זהה לחלוטין לשאלה: נמלים צועדות על מוט באורך מטר אחד, כל אחת במהירות של מטר לדקה, בלי להתנגש ובלי לשנות
כיוון. תוך כמה זמן ייפלו? בנוסח זה אין כאן חידה של ממש: כל אחת מהן תיפול תוך דקה או פחות. תלוי במרחק ההתחלתי שלה מן הקצה שלכיוונו היא צועדת.

7. המתמטיקאים בני המזל

המתמטיקאים הם עם בר מזל. משלמים להם בשביל לשחק. לנוכח המיליארדים המושקעים במחקר מתמטי ובחינוך מתמטי אפשר היה לצפות שהם יידרשו לעסוק בנושאים שימושיים, אבל למעשה ההפך הגמור הוא הנכון. הם מרשים לעצמם לשחק בבעיות כמו חידת הנמלים, ובעיניהם יש לכך ערך. מדוע? משום שאת סוד שימושיותה יוצאת הדופן של המתמטיקה אפשר לראות כבר בחידה הזאת. משתקף בה כוחה העיקרי של המתמטיקה: ההפשטה. הדבר מתבטא, לפני הכול, בהצגת הבעיה. הנמלים בבעיה הן נמלים מתמטיות: נמלים אמיתיות אינן הולכות במהירות אחידה, ואינן מצייתות לחוקים כה פשוטים. הנמלים שלנו מקיימות כללים ברורים ומובחנים. המתמטיקה היא חקר מערכות המצייתות לכללים מוגדרים היטב. אבל עוד יותר מאשר בהצגת הבעיה, ניכרת ההפשטה בפתרונה. הסוד היה במציאת חוקיות פנימית, כאילו גילינו בתצלום רנטגן את המבנה הסמוי שמתחת לדברים. וחוקיות זו התגלתה כשהתעלמנו מפרט מסוים, שהתגלה כטפל - זהותן של הנמלים. ההתעלמות מן הטפל היא תכונה עיקרית של כל חשיבה מתמטית.

ובהפשטות יש יופי. בדיוק מן הסיבה שעליה דובר במאמר הזה: קשה לקלוט אותן לגמרי במודע. את המוחש אנחנו קולטים בקלות. הפשטות כוללות כל כך הרבה, וכל כך רחוקות מהבנתנו הרגילה, שאנחנו לא מבינים אותן עד תומן. וכשכך הוא, אנחנו חשים יופי.

8. תמונה שירית, תמונה מתמטית

הכללה אחת שווה אלף דוגמאות.

(פלוני)

דוגמה אחת שווה אלף הכללות.

(אלמוני)

אני רוצה לספר על עוד קו דמיון אחד בין שירים ומתמטיקה: המשחק בין המוחש והמופשט, בין הפרטי והכללי.

בספרו $latex {12}$ שיחות על שירה מסביר המשורר איתמר יעוז קסט את ההבדל בין שיר ופזמון: הפזמון מדבר על הכללי, ואילו השיר מדבר על הפרטי, כלומר על אירועים אישיים וקונקרטיים. הפזמון אומר “הללויה, ישירו כולם”, השיר אומר “ראיתי ציפור רבת יופי”. שירה לעולם אינה מדברת בלשון הפשטות. היא מדברת בלשון תמונות. “שיר הלילה של הנודד” אינו אומר “הגיבור של השיר נסער. הוא במצוקה”. זה לא שיר, אלא אולי דיווח עיתונאי. השיר מתאר תמונה בחוץ, שהדממה שלה מפחידה. מן התמונה הזאת אנחנו למדים על מה שקורה לגיבור.

דבר דומה נכון גם במתמטיקה. מקובל להאמין שמתמטיקאים חושבים במופשט. זה לגמרי לא נכון. כל מתמטיקאי מקצועי יאמר לכם - הוא חושב בדוגמאות. ההפשטות באות אז מאליהן. והוא חושב גם בתמונות, ממש כמו שעושה השירה. דוגמה מפורסמת לתמונה מתמטית היא מערכת הצירים הקרטזית. מעניין איך הייתה האלגברה מתפתחת לולא התמונה הזאת, שאנשי האלגברה משתמשים בה כל כך הרבה!

הוא שאמר ווירשטרס: “מתמטיקאי שאיננו גם קצת משורר אינו מתמטיקאי מושלם”.

---

השערת Frankl על משפחות סגורות לאיחוד

רון הולצמן

הבעיה הקומבינטורית עליה אכתוב כאן היא קלה לניסוח והבנה, אך ככל הנראה קשה מאוד לפתרון. היא ידועה בשם “Union-closed conjecture”, ונוסחה ע”י המתמטיקאי Peter Frankl בשנת 1979 (אם כי, לפי עדויות מסוימות, היתה ידועה עוד קודם).

אנחנו מתבוננים בקבוצה בת $latex {n}$ איברים, למשל קבוצת המספרים $latex {{1,2,\ldots,n}}$ שתסומן להלן ע”י $latex {[n]}$. תהי $latex {\mathcal{A} = {A_1, A_2, \ldots, A_m}}$ משפחה של $latex {m}$ תת-קבוצות של $latex {[n]}$. האיחוד $latex {A \cup B}$ של שתי קבוצות הוא הקבוצה המכילה אותם איברים שנמצאים לפחות באחת משתי הקבוצות $latex {A,B}$.אנחנו אומרים שהמשפחה $latex {\mathcal{A}}$ סגורה לאיחוד אם לכל שתי קבוצות בה, גם האיחוד שלהן נמצא בה. הנה מספר דוגמאות ל- $latex {\mathcal{A}}$ כזאת:

1. $latex {\mathcal{A} = \mathcal{P} ([n])}$, כלומר משפחת כל התת-קבוצות של $latex {[n]}$.
2. $latex {\mathcal{A}}$ כלשהי הסגורה כלפי מעלה (כלומר, מקיימת $latex {A \in \mathcal{A}, \, A \subseteq B \,\, \Rightarrow \,\, B \in \mathcal{A}}$).
3. הדוגמה הבאה עבור $latex {\mathcal{A} = {\emptyset , {1}, {2}, {1,2}, {1,2,3}}\quad : \, n=3, m=5}$

השערת Frankl: תהי $latex {\mathcal{A}}$ משפחה סגורה לאיחוד, שאיננה המשפחה הטריביאלית $latex {\mathcal{A} = { \emptyset }}$. אזי קיים איבר שנמצא לפחות במחצית מהקבוצות ב- $latex {\mathcal{A}}$.

להשערה זו לא ידועה הוכחה, אם כי היא נבדקה ונמצאה נכונה בדוגמאות רבות. למשל, נעבור על שלוש הדוגמאות דלעיל:

1. $latex {\mathcal{A} = \mathcal{P}([n])}$ $latex {-}$ כאן כל איבר נמצא בדיוק במחצית מהקבוצות.
2. $latex {\mathcal{A}}$ סגורה כלפי מעלה $latex {-}$ לכל איבר $latex {i \in [n]}$, כנגד כל קבוצה $latex {A \in \mathcal{A}}$ שאינה מכילה אותו, ישנה הקבוצה $latex {A \cup {i} \in \mathcal{A}}$ שמכילה אותו, ולכן כל איבר נמצא לפחות במחצית מהקבוצות ב- $latex {\mathcal{A}}$.
3. $latex {\mathcal{A} = { \emptyset , {1}, {2}, {1,2}, {1,2,3}}}$ $latex {-}$ כאן כבר לא כל איבר מתאים: האיבר $latex {3}$ נמצא רק בקבוצה אחת. אבל האיבר $latex {1}$ (וכמוהו גם $latex {2}$) נמצא ב- $latex {3}$ מבין $latex {5}$ הקבוצות ב- $latex {\mathcal{A}}$.

נכניס את הסימון $latex \mathcal{A}_i$ עבור אוסף הקבוצות ב- $latex \mathcal{A}$ שמכילות את האיבר $latex {i}$. כמו-כן, $latex |A|$ יסמן את מספר איברי $latex A$. קל לבדוק, ע”י ספירה בשתי דרכים, כי

$latex \displaystyle \sum_{i=1}^n |\mathcal{A}_i| = \sum_{A \in \mathcal{A}} |A|$

אילו היינו יודעים שהסכום הנ”ל הוא לפחות $latex {\frac{mn}{2}}$, אז הגודל הממוצע של $latex {\mathcal{A}_i}$ היה לפחות $latex {\frac{m}{2}}$, והיינו יכולים להסיק שקיים $latex {i}$ כנדרש בהשערה. לפיכך, די להראות כי הגודל הממוצע של $latex {A \in \mathcal{A}}$ הוא לפחות $latex {\frac{n}{2}}$. בהסתכלות שטחית, נראה שזה אמור להיות נכון, כי הסגירות לאיחוד מחייבת שכנגד קבוצות קטנות ב- $latex {\mathcal{A}}$ יהיו גם קבוצות גדולות. אבל זה לא תמיד נכון: למשל, בדוגמה 3 הגודל הממוצע של הקבוצות ב- $latex {\mathcal{A}}$ הוא $latex {\frac{7}{5}}$, שקטן מ- $latex {\frac{3}{2}}$.

לפיכך, לא ניתן באופן כללי לחזק את השערת Frankl כך שבממוצע איבר יימצא לפחות במחצית מהקבוצות ב- $latex {\mathcal{A}}$. יחד עם זאת, Balla, Bollobás & Eccles הוכיחו כי גרסת הממוצע נכונה במקרה ש- $latex {m \ge \frac{2}{3} \cdot 2^n}$, ובכך הם הוכיחו שהשערת Frankl מתקיימת במקרה זה. ראוי לשים לב, שבדוגמה 3 לעיל שבה גרסת הממוצע נכשלת, מספר הקבוצות $latex {m=5}$ הוא רק מעט יותר נמוך מ- $latex {\frac{2}{3} \cdot 2^n = \frac{16}{3}}$. ניתן להכליל דוגמה זו, כך שתראה שהדרישה שהמשפחה תכיל לפחות שני שלישים מכל התת-קבוצות אכן חיונית לקיום גרסת הממוצע.

כדי לקבל תחושה לגבי נכונות ההשערה, טבעי לבדוק תחילה את המקרים שבהם $latex {\mathcal{A}}$ מכילה קבוצה בעלת מעט איברים. אם $latex {{i} \in \mathcal{A}}$ אז קל לראות (באותה דרך כמו בדוגמה 2 לעיל) ש- $latex {i}$ נמצא לפחות במחצית מהקבוצות. אם $latex {{i,j} \in \mathcal{A}}$ אפשר להראות שלפחות אחד מבין $latex {i,j}$ נמצא לפחות במחצית מהקבוצות. אבל גישה זאת נכשלת עבור $latex {{i,j,k} \in \mathcal{A}}$: יש דוגמאות כאלו, שבהן אף אחד מבין $latex {i,j,k}$ איננו נמצא לפחות במחצית מהקבוצות. למרות זאת, ע”י שימוש בקבוצות קטנות וניתוח של מקרים אפשר לבדוק את קיום השערת Frankl עבור ערכים קטנים למדי של $latex {n}$ ושל $latex {m}$. נכון למועד הכתיבה, התוצאות הטובות ביותר מסוג זה מאמתות את ההשערה כאשר מספר האיברים $latex {n \le 12}$ או כאשר מספר הקבוצות $latex {m \le 50}$. בכיוון המחקר הזה היו שיפורים מעת לעת, וייתכן שעוד יהיו, אבל ספק רב אם הוא יוביל להוכחת ההשערה.

מה ידוע עבור $latex {n}$ ו- $latex {m}$ גדולים? ידועים שלושה חסמים, שטיבם היחסי תלוי בצפיפות של המשפחה (כלומר, כמה גדול הוא מספר הקבוצות $latex {m}$ ביחס למספר האיברים $latex {n}$):

1. (Wójcik) קיים איבר שנמצא לפחות ב- $latex {\frac{24}{5\log_2m} \cdot \frac{m}{2}}$ קבוצות ב- $latex {\mathcal{A}}$.
2. (Balla) קיים איבר שנמצא לפחות ב- $latex {\sqrt{\frac{\log_2n}{n}} \cdot \frac{m}{2}}$ קבוצות ב- $latex {\mathcal{A}}$.
3. (Reimer) קיים איבר שנמצא לפחות ב- $latex {\frac{\log_2m}{n} \cdot \frac{m}{2}}$ קבוצות ב- $latex {\mathcal{A}}$.

בכל החסמים האלה, הגורם הכופל את $latex {\frac{m}{2}}$ עלול להיות קטן. עד היום, לא ידוע אף חסם מהצורה $latex {c \cdot m}$, כאשר $latex {c>0}$ הוא קבוע כלשהו. הוכחה שתמיד קיים איבר שנמצא לפחות ב- $latex {1 \%}$ מהקבוצות ב- $latex {\mathcal{A}}$ תיחשב לפריצת דרך משמעותית.

ביבליוגרפיה:

---

חידות - גיליון 1

אסף שפירא

1. אדם בגובה נתון עומד זקוף מול מראה במימדים נתונים. באיזה מרחק עליו לעמוד, על מנת שיוכל לראות במראה את כפות הרגליים?
2. רון משחק בשלושה מטבעות שמונחים על השולחן. בכל שלב הוא מותח שער דמיוני בין שניים מהמטבעות, ומעביר דרכו את המטבע השלישי. האם יוכל בשבעה צעדים בדיוק להחזיר כל מטבע למקומו המקורי?
3. לשני שחקנים לוח שחמט ואבני דומינו, שכל אחת מהן בגודל המתאים לכסות שתי משבצות בדיוק בלוח השחמט. בתחילה הלוח ריק, וכל שחקן בתורו מכסה באבן דומינו אחת שתי משבצות סמוכות שעוד לא כוסו. השחקן שבתורו לא נותר מקום להניח אבן דומינו נוספת מפסיד במשחק. מי מבין שני השחקנים, הראשון או השני, יכול להבטיח את נצחונו?
4. כעת משחקים שני השחקנים במשחק אחר — בתחילה אין על לוח השחמט אבני דומינו, והשחקן הראשון בוחר במשבצת. על השחקן השני לכסות את המשבצת שאותה בחר השחקן הראשון באבן דומינו, יחד עם אחת מהמשבצות הסמוכות לה. בשלב הבא על השחקן הראשון לבחור משבצת נוספת שעוד לא כוסתה באבן דומינו, ועל השחקן השני לכסות גם אותה. כך ממשיך המשחק, עד שלאחד השחקנים אין מהלך חוקי — או שמגיע תור השחקן הראשון והלוח מלא, או שהגיע תורו של השחקן השני, וכל המשבצות שסמוכות לזו שבחר הראשון כבר מכוסות. השחקן שלא יכול לשחק הוא המפסיד. איזה מבין שני השחקנים יכול להבטיח את נצחונו במשחק זה?
5. נתונים שלושה מספרים ממשיים $latex {x,y,z}$ בקטע $latex {\left(0,1\right)}$. הראו כי לפחות אחד מבין המספרים $latex {x\left(1-y\right),\, y\left(1-z\right),\, z\left(1-x\right)}$ קטן או שווה $latex {\frac{1}{4}}$.
6. נסתכל על קבוצות של מספרים בין $latex {1}$ ל-$latex {n}$ בעלות ממוצע שלם. עבור $latex {n}$ זוגי, האם מספר הקבוצות האלה זוגי או אי-זוגי?
7. עבור איזו כמות של מספרים ממשיים בין $latex {1}$ ל-$latex {2013}$ מובטח ששלושה מתוכם יהיו אורכי צלעותיו של משולש חד זווית?
8. הראו שקיים קבוע $latex {\alpha}$ כך שלכל פולינום $latex {p\left(x\right)}$ ממעלה $latex {100}$, מתקיים ש- $latex {|p\left(0\right)|\le\alpha\int_{0}^{1}|p\left(x\right)|\mbox{d}x}$.
9. נתון משולש $latex {ABC}$, ושלוש נקודות על צלעותיו — $latex {D}$ על הצלע $latex {AB}$, $latex {E}$ על הצלע $latex {BC}$ ו$latex {F}$ על הצלע $latex {AC}$. המשולש $latex {DEF}$ הוא משולש שווה צלעות, ואורכי הקטעים $latex {AD}$, $latex {BE}$ ו$latex {CF}$ שווים זה לזה. הוכיחו ש$latex {ABC}$ גם הוא משולש שווה צלעות.
10. ניב ואורה משחקים במשחק. בכל סיבוב על שניהם לנחש תוצאת הטלה של מטבע הוגן, אחרי כן מטילים את המטבע, וניב ואורה מקבלים נקודה אם שני הניחושים היו נכונים. כך המשחק נמשך, כאשר ניב ואורה יודעים בסוף כל סיבוב מה כל אחד ניחש ומה היתה תוצאת ההטלה, אך אין להם יכולת לתקשר זה עם זה מרגע שהמשחק החל. ניב יכול להסתמך בניחושים שלו רק על מה שלמד בסיבובים הקודמים, בהתאם לסיכום שעשה עם אורה לפני תחילת המשחק. לאורה, לעומת זאת, יש יכולת ניבואית — רגע לפני שהמשחק מתחיל היא יכולה לגלות את כל תוצאות ההטלות שיתקבלו. לפני המשחק, כאשר אורה וניב מתאמים כיצד לפעול, הם יודעים על יכולתה הניבואית של אורה, אבל היא עוד לא יכולה לגלות את תוצאות ההטלות העתידיות. נסו להציע אסטרטגיה, שבה מספר הנקודות הממוצע שיקבלו ניב ואורה אחרי מספר רב של מהלכים יהיה כמה שיותר גדול.