נטגר גליון 10
דבר העורך
רון אהרוני
מי היה המתמטיקאי הגדול של כל הדורות? שאלה טפשית, כנראה. יש והיו כל כך הרבה מתמטיקאים דגולים בעולם. אבל מבחינת האלגנטיות של התוצאות, אין הרבה מתחרים למתמטיקאי השוויצארי לאונרד אוילר ($latex {1707-1783}$). הוא היה גאון (בין השאר) בחישוב טורים אינסופיים, ובשימוש בהם לתחומים אחרים, למשל קומבינטוריקה. אחת מתוצאותיו המפורסמות (היו לו המון תוצאות מפורסמות, הוא היה גם אחד המתמטיקאים הפוריים ביותר מאז ומעולם) הייתה ההוכחה ש-$latex {\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\ldots = \frac{\pi^2}{6}}$ - תוצאה מפתיעה ביותר. במאמר יפה מספר אליהו לוי על ההוכחה של המשפט הזה, וגם מעלה הגיגים על האקראיות של הפיתוח העשרוני של $latex {\pi}$.
אנה ליזהטוב חוזרת אלינו, הפעם לא עם עלילותיו של יסולא פז (שלאחרונה אין רואים אותו בפקולטה למתמטיקה, וידידיו ומוקיריו מעט מודאגים). המאמר שלה מספר על תגלית מהפכנית משנת $latex {1931}$, שיש המכנים אותה "התגלית המתמטית החשובה של המאה העשרים". זהו המשפט של גדל, שבלשון מפושטת מאוד אפשר לנסח כ"לא כל דבר נכון אפשר להוכיח". כדי לדעת במה מדובר במדויק, קראו!
גם המדור "השערת החודש" חוזר, עם השערה על ריבועים לטיניים שנראית אזוטרית (כלומר צדדית), אבל יש לשער שהיא דווקא מסתירה מאחוריה סודות מעניינים.
ויש לנו שותף חדש: דני לובזנס הסכים ברוב טובו לערוך את מדור הבעיות. דני הוא פותר חידות בעל שם, ואנו מאחלים לו הצלחה רבה בתפקידו החדש.
האם סביר לטעון שπ הוא "אקראי"?
אליהו לוי
זהו כמעט "קונצנזוס", כאשר כותבים על $latex {\pi}$ (או על קבועים אחרים כמו $latex {e}$) לאמר ש "אין שום ספק ש… יש ל $latex {\pi}$ תכונת "אקראיות" זו או אחרת , אפילו אם אין אנו יודעים (לעת עתה…) להוכיח זאת". למשל:
א. האם בפיתוח העשרוני של $latex {\pi}$ מופיעה כל סיפרה אינסוף פעמים? או אולי ממקום מסויים והלאה לא תופיע יותר הסיפרה $latex {6}$, למשל? לא רק שאין אנו יודעים, אין למתמטיקאים כיום מושג איך להתחיל לגשת לבעייה זו, במובן של מציאת הוכחה לכאן או לכאן. אבל כולם כותבים ש"מובן מאליו" שמתקיים הרבה יותר מזה, למשל שהשכיחות של כל סיפרה (המוגדרת כגבול של השכיחות בין $latex {N}$ הספרות הראשונות כאשר $latex {N\rightarrow\infty}$) היא $latex { 10\%}$, שהשכיחות של כל זוג ספרות להופיע בסמיכות (למשל 14) הוא $latex {1\%}$, בקיצור - שאפשר לקחת את סידרת הספרות של $latex {\pi}$ כסידרה "אקראית".
ב. למרות שזה "מובן מאליו…" הוכיחו אחרי מאמצים רבים במאה ה-$latex {19}$ ש $latex {\pi}$ מספר אירציונלי, ואפילו מספר טרנסצנדנטי, כלומר לא מקיים שום משוואה אלגברית מעל הרציונליים, כלומר משוואה שמורכבת מארבע פעולות החשבון ומקדמים רציונליים. אבל מה אם נוסיף עוד פעולות, כגון חזקה? האם $latex {\pi^\pi}$, $latex {\pi^{\pi^\pi}}$, $latex {\pi^{\pi^2+1}}$ לא יכולים להיות רציונליים? - איש לא יודע איך לגשת לזה. ולגבי מספרים גדולים מאוד, מעבר לאפשרויות החישוב אפילו של האדירים שבמחשבים - אולי
$latex \pi^{\pi^{\cdot^{\cdot^{\cdot^\pi}}}}$
($latex {10}$ פעמים $latex {\pi}$) הוא מספר שלם? איש לא יכול להוכיח שלא. למרות ש"כולם" בטוחים שדבר כזה לא יכול להיות…
אני טוען שהבטחון ב"אקראיות" הזאת של $latex {\pi}$ היא ממש דעה קדומה. הלא $latex {\pi}$ הוא מספר מאוד מאוד מסויים ומאוד מאוד מיוחד - היחס בין היקף מעגל לקוטרו. אז למה שהוא לא יקיים שוויונות מיוחדים, שנמצא ונוכיח בעתיד?
(אותו דבר אפשר להגיד על סידרת המספרים הראשוניים - כולם מצפים, ולפעמים מוכיחים ויודעים, שיהיו להם תכונות אקראיות. (כמובן לא, למשל ש- $latex {50\%}$ מהם זוגיים…) אבל גם זו סידרה מאוד מאוד מיוחדת, ולמה שלא יהיו לה תכונות מיוחדות?. שימו לב לכך שהעמדנו מספר ממשי מסויים - $latex {\pi}$ - מול סידרה מסויימת של טבעיים - סידרת הראשוניים. לפחות מבחינת העוצמה, במובן של תורת הקבוצות, יש לקבוצת הממשים ולקבוצת סדרות הטבעיים אותה עוצמה - עוצמת הרצף.)
אתנחתא קצרה: התבוננו במספר
$latex \displaystyle \frac{\ln[(320\cdot2001)^3+720+24]}{\sqrt{163}}$
ב $latex {29}$ הספרות הראשונות הוא שווה ל $latex {\pi}$, אבל אחר כך לא! (רק מחשבון בדיוק גבוה ירגיש בהבדל). זה לא "סתם" - יש לזה סיבה במתמטיקה די "גבוהה".
ואכן, לפעמים $latex {\pi}$ מקיים שוויונות (אלא שכבר התרגלנו אליהם, ולכן לא רואים אותם כדוגמת נגד ל"אקראיות" של $latex {\pi}$…).
למשל, נתבונן בטור האינסופי
$latex \sum_{n=1}^\infty\frac1{n^2}=1+\frac1{2^2}+\frac1{3^2}+\ldots \ \ \ \ \ (1)$
מתקיים
$latex \frac1{n^2}\le\frac1{n(n-1)}=\frac1{n-1}-\frac1{n},\qquad n=2,3,\ldots$
לכן הטור (1) קטן מהטור
$latex 1+(1-\frac12)+(\frac12-\frac13)+(\frac13-\frac14)+\ldots=2$
ולכן יש ל (1) סכום סופי, אומרים שהוא מתכנס. נעיר שסכום הטור
$latex \sum_{n=1}^\infty\frac1{n}=1+\frac1{2}+\frac1{3}+\ldots$
הוא $latex {\infty}$, כי סכום האיברים מהמקום ה $latex {2^k+1}$ עד המקום ה $latex {2^{k+1}}$ גדול מ $latex {1/2}$ - בידקו.
(וכולם יודעים שאם $latex {|a|<1}$ אזי הטור הגיאומטרי $latex {1+a+a^2+a^3+\ldots}$ מתכנס וסכומו $latex {1/(1-a)}$, למשל $latex {1+2^{-1}+2^{-2}+2^{-3}+\ldots=2}$.)
אם כך, הטור (1) הוא אחד הטורים המתכנסים הפשוטים ביותר שאפשר לבנות. יש לו סכום סופי. האם קיבלנו כך קבוע מתמטי חדש, כדוגמת $latex {\pi}$, $latex {e}$, $latex {\ln2}$?
משפט.
סכום הטור (1) הוא $latex {\displaystyle{\frac{\pi^2}{6}}}$.
הוכחה.
ההוכחה הבאה נראית כאילו "נפלה מהשמים", אבל המניע לה היא תורת "טורי פוריה" $latex {Fourier}$.
נתבונן בפונקציות חסומות (תמיד נניח שהן מספיק "הגונות" כך שלאינטגרלים שנכתוב יש משמעות) המוגדרות באינטרוול $latex {[0,\frac\pi2]}$. לגבי פונקציות $latex {f}$, $latex {g}$ כאלה נשתמש בסימון
$latex \displaystyle \left\langle f,g\right\rangle:=\int_0^{\frac\pi2}f(x)g(x)\,dx.$
$latex {\left\langle f,g\right\rangle}$ היא מעין "מכפלה", רק שהיא נותנת משתי פונקציות מספר. היא מקיימת את חוקי החילוף והפילוג:
$latex \displaystyle \left\langle f,g\right\rangle=\left\langle g,f\right\rangle,\qquad \left\langle f+g,h\right\rangle=\left\langle f,h\right\rangle+\left\langle g,h\right\rangle.$
בנוסף לכך, עבור כל $latex {f}$
$latex \displaystyle \left\langle f,f\right\rangle=\int_0^{\frac\pi2}f^2(x)\,dx\ge0.$
ניזכר בכמה נוסחאות טריגונומטריות:
$latex \sin(2n-1)x\sin(2m-1)x=\frac{1}{2}[\cos2(m-n)x-\cos2(m+n-1)x].$
$latex \int_0^{\frac\pi2}\cos2kx\,dx=\frac1{2k}\sin2kx|_0^{\frac\pi2}=0,\qquad k\ne0$
$latex \left\langle\sin(2n-1)x,\sin(2m-1)x\right\rangle=0,\qquad m,n=1,2,\ldots,\quad m\ne n$
$latex \left\langle\sin(2n-1)x,\sin(2n-1)x\right\rangle= \int_0^{\frac\pi2}\frac{1}{2}[1-\cos2(2n-1)x]\,dx=\frac\pi4 $
תהי $latex {f}$ פונקציה חסומה על $latex {[0,\frac\pi2]}$.
$latex a_{2n-1}:= \left\langle f,\sin(2n-1)x\right\rangle,\qquad n=1,2,\ldots$
$latex g:= \frac\pi4f-[a_1\sin x-a_3\sin 3x-\ldots-a_{2N-1}\sin(2N-1)x]$
$latex 0\le\left\langle g,g\right\rangle = \left(\frac\pi4\right)^2\left\langle f,f\right\rangle- 2\frac\pi4[a_1^2+a_2^2+\ldots a_{2N-1}^2]+ \frac\pi4[a_1^2+a_2^2+\ldots a_{2N-1}^2]=$
$latex =\left(\frac\pi4\right)^2\left\langle f,f\right\rangle-\frac\pi4[a_1^2+a_2^2+\ldots a_{2N-1}^2]$
$latex a_1^2+a_2^2+\ldots a_{2N-1}^2\le\frac\pi4\left\langle f,f\right\rangle $
ומכאן שהטור $latex {\sum a_{2n-1}^2}$ מתכנס - יש לו סכום סופי. לכן עבור כל $latex {\epsilon>0}$ יש רק מספר סופי של $latex {a_{2n-1}^2}$-ים שגדולים מ-$latex {\epsilon}$. ממקום מסויים יהיה $latex {a_{2n-1}^2<\epsilon}$. במלים אחרות, $latex {a_{2n-1}\rightarrow 0}$.
ניקח כעת
$latex \displaystyle f(x):=\frac{x}{\sin x},\qquad 0<x\le\frac\pi2,\qquad f(0):=1$
נזכיר שכאשר $latex {x\rightarrow 0}$ , $latex {\frac{x}{\sin x}\rightarrow 1}$, ולכן $latex {f}$ רציפה וחסומה.
$latex \displaystyle a_{2n-1}=\left\langle f,\sin(2n-1)x\right\rangle=\left\langle x,\frac{\sin(2n-1)x}{\sin x}\right\rangle\rightarrow 0.$
מהו $latex {\frac{\sin(2n-1)x}{\sin x}}$ ? מתקיים
$latex \cos2kx\sin x = \frac{1}{2}[\sin(2k+1)x-\sin(2k-1)x] $
$latex \cos2x+\cos4x+\ldots\cos2(n-1)x]\sin x= $
$latex \frac{1}{2}[(\sin3x-\sin x)+(\sin5x-\sin3x)+\ldots+(\sin(2n-1)x-\sin(2n-3)x)]=$
$latex \frac{1}{2}[\sin(2n-1)x-\sin x]$
$latex \frac{\sin(2n-1)x}{\sin x} = 1+2[\cos2x+\cos4x+\ldots+\cos2(n-1)x]. $
וקיבלנו
$latex \displaystyle \left\langle x,1+2[\cos2x+\cos4x+\ldots+\cos2(n-1)x]\right\rangle\rightarrow 0,$
כלומר
$latex \displaystyle \left\langle x,1\right\rangle+2[\left\langle x,\cos2x\right\rangle+\left\langle x,\cos4x\right\rangle+\ldots+\left\langle x,\cos2(n-1)x\right\rangle]\rightarrow 0. \ \ \ \ \ (2)$
אבל
$latex \displaystyle \left\langle x,1\right\rangle = \int_0^{\frac\pi2}x\,dx=\frac{1}{2} x^2|_0^{\frac\pi2}=\frac{\pi^2}8.$
$latex \left\langle x,\cos2kx\right\rangle = \int_0^{\frac\pi2}x\cos2kx\,dx= \int_0^{\frac\pi2}\left[\frac1{2k}x\sin2kx\right]'\,dx- \frac1{2k}\int_0^{\frac\pi2}\sin2kx\,dx=$
$latex =\frac1{2k}x\sin2kx|_0^{\frac\pi2}+\frac1{4k^2}\cos2kx|_0^{\frac\pi2}= 0+\frac1{4k^2}[(-1)^k-1] $
זה שווה $latex {0}$ אם $latex {k}$ זוגי ו $latex {-\frac1{2k^2}}$ אם $latex {k}$ איזוגי.
ולבסוף (2) מקבלת את הצורה
$latex \displaystyle \frac{\pi^2}8=\frac1{1^2}+\frac1{3^2}+\frac1{5^2}+\ldots$
אבל
$latex \frac1{1^2}+\frac1{2^2}+\frac1{3^2}+\ldots=$
$latex =\frac1{1^2}+\frac1{3^2}+\frac1{5^2}+\ldots+ \frac14\left[\frac1{1^2}+\frac1{2^2}+\frac1{3^2}+\ldots\right].$
$latex \frac34\left[\frac1{1^2}+\frac1{2^2}+\frac1{3^2}+\ldots\right]=$
$latex =\frac1{1^2}+\frac1{3^2}+\frac1{5^2}+\ldots. $
ולבסוף
$latex \displaystyle \frac1{1^2}+\frac1{2^2}+\frac1{3^2}+\ldots= \frac43\left[\frac1{1^2}+\frac1{3^2}+\ldots\right]= \frac43\cdot\frac{\pi^2}8=\frac{\pi^2}6$
וגמרנו.
מקובל לסמן ב $latex {\zeta(m)}$ (פונקצית זתא של אוילר ורימן) את סכום הטור
$latex \displaystyle \zeta(m):=\sum_{k=1}^\infty\frac1{k^m}=1+\frac1{2^m}+\frac1{3^m}+\ldots.$
ראינו ש $latex {\zeta(2)=\frac{\pi^2}6}$. גם $latex {\zeta(m)}$ עבור $latex {m=3,4,\ldots}$ הוא סופי (הטור מתכנס)- ככל ש $latex {m}$ גדול יותר אברי הטור יותר קטנים ולכן "מתכנסים יותר מהר" - הבהירו.
עבור $latex {m}$ זוגי אפשר לבטא את $latex {\zeta(m)}$ ככפולה רציונלית של חזקה של $latex {\pi}$, בדומה ל $latex {\zeta(2)}$. מכאן שהם אירציונליים (כי $latex {\pi}$ טרנסצנדנטי). למשל:
$latex \displaystyle \zeta(4)=\frac{\pi^4}{90},\qquad\zeta(6)=\frac{\pi^6}{945},\qquad \zeta(8)=\frac{\pi^8}{9450}.$
באשר ל $latex {m}$ איזוגי, עד כמה שידוע לי לא ידועות שום נוסחאות המקשרות אותם לקבועים כמו $latex {\pi}$. בערך ב $latex {1980}$ הוכיח $latex {Roger Apéry}$ ש $latex {\zeta(3)}$ אירציונלי. לגבי $latex {\zeta(5),\zeta(7),\ldots}$ אפילו זה לא ידוע, עד כמה שידוע לי.
השערת רייזר על ריבועים לטיניים
רון אהרוני
ריבוע לטיני מסדר $latex {n}$ הוא ריבוע (מטריצה) מסדר $latex {n \times n}$ שממולא במספרים מ-$latex {1}$ עד $latex {n}$, כך שכל מספר מופיע פעם אחת בדיוק בכל שורה ופעם אחת בדיוק בכל עמודה.
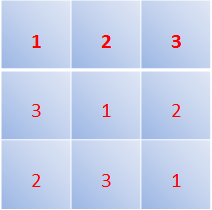
ריבוע לטיני מסדר $latex {3}$.
טרנסוורסל בריבוע לטיני הוא אוסף משבצות, שנמצאות בשורות שונות, עמודות שונות, ומכילות מספרים שונים. גודל של טרנסוורסל הוא מספר המשבצות שבו. טרנסוורסל מגודל $latex {n}$ נקרא מלא.

טרנסוורסל מלא לריבוע הלטיני שלנו.
בתחילת שנות ה-$latex {70}$ ניסח מתמטיקאי אמריקני בשם רייזר ($latex {Ryser}$) את ההשערה הבאה:
בכל ריבוע לטיני מסדר אי זוגי יש טרנסוורסל מלא.
ל-$latex {n}$ זוגי ההשערה לא נכונה. הסתכלו באיור. זהו לוח החיבור של המספרים מודולו (שארית) מ-$latex {4}$. אין בו טרנסוורסל מלא.
משפט 1 - לוח החיבור של המספרים מודולו (שארית) מ-$latex {2k}$ הוא ריבוע לטיני, שאין לו טרנסוורסל מלא.
הוכחה: את העובדה שזהו ריבוע לטיני נשאיר כתרגיל. נוכיח רק שאין טרנסוורסל מלא. נניח שיש טרנסוורסל כזה. מכיוון שמופיעים בו כל המספרים בין 1 ל-$latex {2k}$, סכום איבריו הוא $latex {1+2+\ldots +2k}$, שעל פי הנוסחה לסכום של טור גיאומטרי שווה ל-$latex {\frac{(2k+1)2k}{2}=(2k+1)k}$. מצד שני, מכיוון שכל עמודה בלוח החיבור וכל שורה בלוח מיוצגות על ידי משבצת אחת בטרנסוורסל, ומכיוון שבכל משבצת מופיע סכום השורה והעמודה שלה, יוצא שסכום המספרים במשבצות הוא $latex {2(1+2+\ldots+2k)=(2k+1)2k}$. נזכיר שכל החישובים האלה הם מודולו (שארית מ-) $latex {2k}$. ההפרש בין שתי התוצאות בשתי דרכי החישוב השונות הוא $latex {(2k+1)(2k-k)=(2k+1)k}$, שהשארית שהוא משאיר בחלוקה ב-$latex {2k}$ היא $latex {k}$, שאינו $latex {0}$ מודולו $latex {2k}$. אם כן, יצאו לנו שתי תוצאות שונות - סתירה.
תלמיד תיכון ממקדוניה, בודן אסובסקי, הוכיח שהשערת רייזר נכונה ללוח החיבור של חבורות מסדר אי זוגי. מה ידוע על ההשערה? לא הרבה. $latex {Shor}$ ו-$latex {Hatami}$ הוכיחו שיש טרנסוורסל בגודל $latex {n - 5 \log_2^2n}$. זה יפה, אבל לא נותן רמז מדוע ההשערה נכונה. רמז יותר טוב ניתן על ידי שטיין, ששיער את הדבר הבא: בריבוע $latex {n \times n}$ שבו כל אחד מן המספרים $latex {1,2, \ldots ,n}$ מופיע $latex {n}$ פעמים יש טרנסוורסל מגודל $latex {n-1}$ (כלומר כמעט מלא).
ברואלדי ושטיין שיערו קודם לכן שבריבוע לטיני מסדר זוגי יש טרנסוורסל כמעט מלא. זוהי הכללה גם של ההשערה הזאת.
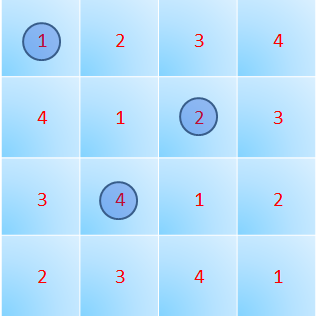
אגב, בהשערת שטיין אין הבדל בין המקרה הזוגי והאי זוגי. התרגיל הבא מראה זאת:
תרגיל 1 - לכל $latex {n}$ מצאו ריבוע $latex {n \times n}$ שמכיל כל אחד מן המספרים $latex {1, \ldots ,n}$ כל אחד בדיוק ב-$latex {n}$ משבצות, שאין לו טרנסוורסל מלא.
האם השערות כאלה חשובות? זה תלוי בטיב הפתרון. במקרה זה אני אישית מאמין שהפתרון יגלה מבנה עמוק, ויוביל לתובנות קומבינטוריות שיקרינו גם על תחומים אחרים.
התייחסות עצמית ומשפט גֶדֶל
אנה ליזהטוב
א. התוכנית של הילברט
גיל 24 הוא כנראה גיל טוב לחולל בו מהפכות מדעיות. אייזק ניוטון היה בגיל הזה ב"שנת הפלאים" שלו, 1666, שבה פיתח את תורת הכבידה, את החשבון הדיפרנציאלי והאינטגרלי, וגילה את חוקיה הבסיסיים של האופטיקה המודרנית. איינשטיין היה בגיל זה כאשר יצר את תורת היחסות הפרטית. קורט גדל (Kurt Gödel, 1906-1978) האוסטרי היה בגיל הזה כאשר הוכיח משפט ששינה את דרך ראייתנו את המתמטיקה.
כפי שסיפרתי בגיליוננו הקודם, בסוף המאה ה-19 הראה מתמטיקאי גרמני בשם גוטלוב פרֶגֶה שאפשר לחקור בצורה מתמטית את החשיבה האנושית, ובמיוחד – את החשיבה המתמטית. התחום שנולד נקרא "לוגיקה מתמטית". רעיונותיו של פרגה זכו להמשך בתחילת המאה ה-20 בידי מתמטיקאים רבים, שהמובילים ביניהם היו ראסל, וויטהד והילברט. התקוות הרקיעו שחקים. פרגה לימד אותנו שאפשר לתאר את תהליך ההוכחה המתמטית במונחים מכאניים. הוא הראה שהוכחה מתמטית היא בסך הכול סידרת סימנים על נייר, המצייתים לכללים מוגדרים היטב. פירוש הדבר הוא שאפשר לבדוק בצורה מכאנית אם סידרת סימנים היא הוכחה או לא. בלשון ימינו היינו מבטאים זאת בכך שגם מחשב יכול לבדוק אם סידרת סימנים על נייר היא הוכחה. אבל אם כך הוא, אפשר להעז לשאול: אולי יוכל המחשב גם למצוא הוכחות? האם אפשר לכתוב תוכנת מחשב, שבהינתן לה טענה (שאף היא, כמובן, אוסף סמלים על נייר) תוכיח אותה, או תוציא כפֶלֶט: "לא, אי אפשר להוכיח את הטענה הזאת"? תארו לכם איזה עולם נפלא היה זה! המתמטיקאים היו יכולים לפרוש מעבודתם, ולהפקיד את ההוכחות בידי תוכניות מחשב. ואפילו אם אי אפשר היה מבחינה מעשית לכתוב תוכנית כזו, אבל ניתן היה להראות בעיקרון שהיא קיימת, גם אז הייתה לכך חשיבות תיאורטית עצומה.
שאלות מסוג זה נשאלו בשלושת העשורים הראשונים של המאה ה-20. באותו זמן, כמובן, עוד לא היה המחשב קיים, ובמקום "תוכנית מחשב" השתמשו בני הדור במונח "אלגוריתם", שהוא מרשם שמכתיב סדר מדויק של פעולות, כמו מתכון לאפיית עוגה. בשפה זו, הלוגיקאים של אותה תקופה חיפשו אלגוריתם שבודק אם נוסחה ניתנת להוכחה או לא, ואם הוא מחליט שיש הוכחה הוא גם יודע למצוא אותה. הילברט העמיד בפני בני דורו את האתגר של מציאת אלגוריתם כזה. זה היה חלק מתוכנית כללית שזכתה לשם "הפרוגרמה של הילברט".
באותה תקופה התעניינו הלוגיקאים יותר מכל בתורת המספרים. מערכת אקסיומות לתורת המספרים, שנוסחה ב-1889 על ידי האיטלקי פֶּאָנוֹ (Giuseppe Peano,
1858-1932) נחשבה אז למילה האחרונה, והכול סברו שהיא ממצה את כל מה שניתן לדעת על המספרים. פירוש הדבר הוא שבני התקופה האמינו, או לפחות קיוו, שמערכת פֶּאָנו תהיה מסוגלת להוכיח כל מה שנכון, כלומר כל טענה נכונה על המספרים הטבעיים. רכיב עיקרי בפרוגרמה של הילברט היה חיפוש אחרי אלגוריתם שיחליט לגבי כל טענה הנוגעת למספרים אם היא נכונה או לא. אם האלגוריתם ("תוכנית המחשב") יחליט שהטענה נכונה, הוא יידרש גם למצוא לטענה הוכחה מאקסיומות פאנו.
ב. בלש שיטתי אך לא יעיל
יש אלגוריתם טבעי ומתבקש מעצמו, לבדוק אם נוסחה ניתנת להוכחה: לנסות את כל האפשרויות. כאמור, אף אם קשה למצוא הוכחות, קל לבדוק אם סידרת סימנים על נייר היא הוכחה לטענה נתונה (בתנאי שההוכחה מפורשת עד לפסיק האחרון!) דרך פשוטה לבחון אם נוסחה נתונה ניתנת להוכחה או לא היא על כן לעבור אחת לאחת, על פי סדר שיטתי, מקצרות לארוכות, על כל סדרות הסימנים האפשריות, ולכל סידרת סימנים לבדוק אם היא הוכחה לטענה המבוקשת. כמובן, אין זו דרך יעילה במיוחד. היא דומה לחוקר משטרה המנסה לפתור מקרה רצח על ידי בדיקת כל האנשים בעולם, אחד לאחד. כשם שחקירות משטרתיות אינן נערכות בדרך זו, כך גם אף אחד לא ינסה למצוא הוכחות למשפטים מתמטיים על ידי כתיבת סימנים מִקריים על נייר, ובדיקה אם במקרה הם יצרו הוכחה למשפט. אבל בשלב זה איננו מחפשים אלגוריתם יעיל – אנחנו מחפשים אלגוריתם כלשהו!
אולם מעבר לחוסר היעילות יש בעיה עקרונית יותר עם השיטה הזאת, והיא שאין יודעים מתי לעצור. האלגוריתם של חוקר מקרי הרצח אינו יעיל, אבל הוא אפשרי, משום שיש רק מספר סופי של בני אדם בעולם, והאלגוריתם יסתיים בשלב כלשהו. במקרה של הוכחות מתמטיות המצב שונה. אם בשלב כלשהו במהלך חיפושינו נמצא הוכחה, מה טוב. אבל מה נעשה אם בדקנו מיליון סדרות של סימנים, ואף אחת מהן אינה ההוכחה המבוקשת? כמובן, נוכל לעבור לסידרה המיליון ואחת, אך לעולם לא נוכל לעצור ולהכריז: "לא הצלחנו למצוא הוכחה, ולכן הטענה אינה נכונה". תמיד יש אפשרות שבצעד הבא היינו מוצאים את ההוכחה, לו רק היינו ממשיכים. מחפשי נפט עומדים בפני הדילמה הזאת, אלא שבמקרה שלהם יש לפחות גבול תיאורטי: אם קדחו והגיעו לצד השני של כדור הארץ, זהו אות מובהק לכישלון. במקרה של הוכחות אין שום שלב שבו אמורים להתייאש. אין חסם תיאורטי לאורכן של הוכחות.
רעיון הבדיקה של סדרות מקריות של סימנים נכשל אפוא. אבל אפשר לנסות דבר מה קצת יותר מתוחכם: לערוך מירוץ בין הטענה הנבדקת לבין שלילתה. כלומר, לבדוק את כל הסדרות של סימנים על נייר, בצורה שיטתית, ולבחון שני דברים במקביל: האחד, אם סידרת הסימנים היא הוכחה לטענה; השני – אם הסידרה היא הוכחה לשלילתה של הטענה. אם הטענה ניתנת להוכחה, נגיע בסופו של דבר לסידרת סימנים שמהווה הוכחה לה. אם השלילה של הטענה ניתנת להוכחה, נגיע בסופו של דבר לסידרת סימנים שהיא הוכחה לשלילה. כך נצליח להוכיח כל טענה, או להוכיח את שלילתה!
ג. משפט גדל ושברה של תוכניתו של הילברט
אלא שכאן נכנס לתמונה גֶדֶל. הוא הראה שהשיטה הזאת לא תעבוד, מסיבה מפתיעה, שמאחוריה עומדת עובדה יסודית: ייתכן בהחלט שאף אחד משני הצדדים לא ינצח במירוץ. יש טענות שגם הן, וגם שלילתן, אינן ניתנות להוכחה. וכיוון שכך, החיפוש השיטתי לא יביאנו לפתרון. אין שום ביטחון שנעצור אי פעם. אין וודאות שבשלב כלשהו תוכח הטענה או תוכח שלילתה.
המשפט האומר שיש טענות שהן ושלילתן אינן ניתנות להוכחה נקרא "משפט אי השלֵמוּת של גֶדֶל". גדל הוכיח הרבה משפטים, אבל כשאומרים "משפט גדל" הכוונה אליו. המשפט אומר שתורת המספרים, כפי שניסח אותה למשל פֶּאָנו, "אינה שלמה", במובן זה שאינה יודעת להכריע טענות מסוימות, לפחות ככל שהדברים נוגעים להוכחות.
משפט אי השלמות הוא רק קצה קצהו של גוף ידע עמוק ומסעיר שבנה גדל. במבט של כמעט שמונים שנים לאחור, לא פחות חשובות היו טענות אי אפשרות אחרות שהוכיח. למשל, שאין אלגוריתם (תוכנית מחשב) שיכול לבדוק לכל נוסחה אם היא ניתנת להוכחה או לא (הכוונה לתוכנית מחשב אחת, שתעבוד לכל הנוסחאות!); אין אלגוריתם שבודק עבור כל נוסחה אם היא נכונה או לא (נכונוּת וניתנוּת להוכחה הם דברים שונים – זוהי מסקנה נוספת מתורתו של גדל. יש נוסחאות שהן נכונות, אבל אינן ניתנות להוכחה) ואי אפשר להוכיח בתוך תורת המספרים שתורת המספרים היא חסרת סתירה. משמעם של כל אלה היה הפרכה מוחלטת של התוכנית של הילברט, על כל פרטיה ורכיביה.
טענות אי האפשרות שהוכיח גדל משכו את תשומת ליבו של אנגלי צעיר בשם טיורינג (Alan Turing, 1912-1954). בנוסף להיותו מתמטיקאי יוצא דופן, היה טיורינג גם בעל כשרון מכאני, והוא רצה לתת לטענותיו של גדל לבוש מוחשי יותר, שנוגע למכונות. לשם כך הוא המציא ב-1936 מודל תיאורטי ראשון למחשב, שפעולתו היא כְּשֶׂל מחשב בן ימינו. מכאן עד לבנייתו של המחשב הייתה הדרך קצרה. טיורינג עצמו היה שותף בזמן מלחמת העולם השנייה לבנייתו של מחשב פרימיטיבי, כחלק ממאמץ פיצוח הצופן הגרמני לתקשורת עם צוללות. תורתו של גדל הייתה אפוא צעד משמעותי ביותר בכיוון יצירתו של המחשב. אין זה פלא שרבים רואים בה את המהפכה המתמטית החשובה ביותר של המאה ה-20.

קורט גדל, מתמטיקאי אוסטרי, 1978-1906.[1]
ד. המעגליות
"הַתְּפִלּוֹת יָצְרוּ אֶת הָאֱלֹהִים,
הָאֱלֹהִים יָצַר אֶת הָאָדָם
וְהָאָדָם יוֹצֵר תְּפִלּוֹת
שֶׁיּוֹצְרוֹת אֶת הָאֱלֹהִים שֶׁיּוֹצֵר אֶת הָאָדָם."
("אלים מתחלפים, התפילות נשארות לעד", יהודה עמיחי, מתוך "פתוח סגור פתוח", הוצאת שוקן)
את הרעיון להוכחת משפט אי השלמות, כך סיפר גדל עצמו, הוא נטל מפרדוקס ששמו "פרדוקס רישאר (Richard)". גם הפרדוקס הזה, כמו פרדוקס ראסל, הוא פרודיה על שיטת האלכסון של קנטור, וגם הוא מבוסס על אותו רעיון: התייחסות עצמית. כבר אמרנו שכל פרדוקס מבוסס על תרמית, כלומר הנחה שגויה סמויה שמובילה למסקנה גלויה בלתי אפשרית. מתברר שבין כל התרמיות האפשריות יש למעגליות מקום של כבוד. במרבית הפרדוקסים ההטעיות מתגלות במהרה, וחשיפתן מהווה לא יותר מאשר פתרון חידה, לעתים קשה למדי אבל כמעט אף פעם לא קשה מאוד. אבל יש כמה פרדוקסים שהחזיקו מעמד לאורך שנים רבות, והם זוכים ליחס של כבוד כאילו חבויה בהם סתירה אמיתית. למרבה הפלא, בכל הפרדוקסים מן הסוג הזה ההטעיה מבוססת על אותה תרמית – מעגליות, כלומר על הגדרה של דבר בעזרת עצמו. בעיקרון, התרמית בפרדוקסים כאלו אינה שונה מזו של אדם המגדיר מספר כ"עצמו ועוד 1", מניח שאכן יש מספר כזה במציאות, ואחר כך קורא בבהלה – "הצילו! סתירה!", משום שמצא מספר השווה לעצמו ועוד 1. אומנם, הגדרת מספר כ"עצמו ועוד 1" היא שקופה מכדי שיתייחסו אליה ברצינות. אבל עם לא הרבה מאמץ אפשר להסוות את ההגדרה המעגלית, ואז נוצר פרדוקס בעל איצטלה של מהוּגנוּת. מוחו של האדם אינו בנוי כנראה לחשוף את המעגליות בקלות.
המפורסם בין הפרדוקסים מן הסוג הזה הוא "פרדוקס השקרן", שמקורו ביוון במאה החמישית לפני הספירה, והופיע לראשונה ברשימה מפורסמת של פרדוקסים שנערכה בידי אֶוּבּוּלידֶס. הוא מציג את המשפט הבא:
משפט זה שקרי.
חישבו על ערך האמת של המשפט הזה: אם המשפט אמיתי, כי אז, על פי תוכנו, הוא שקר. אבל אם הוא שקר, כי אז, שוב על פי תוכנו, הוא אמיתי. כמו בפרדוקס ראסל מצאנו בכך טענה שהיא נכונה אם ורק אם אינה נכונה, מצב בלתי אפשרי בעליל. הפרדוקס הזה הדריך את מנוחתם של דורות רבים של פילוסופים, ונהרות של דיו נשפכו עליו. למעשה, התרמית שמאחוריו פשוטה מאוד, ואינה שונה בהרבה מהגדרת מספר כ"עצמו ועוד 1". המושג המוגדר מעגלית בפרדוקס הוא ערך האמת של המשפט. משפט אינו בא לעולם עם ערך אמת צמוד לדש בגדו. כדי לחשב את ערך האמת של משפט יש לטרוח בהשוואת המשפט עם המציאות. אלא שהמשפט הזה מדבר על ערך האמת של עצמו, ולכן חלק המציאות שאיתו צריך להשוות את המשפט אינו אלא ערך האמת עצמו, כלומר תוצאת הבדיקה הנוכחית. כך מוגדר ערך האמת של משפטו של השקרן בעזרת עצמו. למעשה, הוא מוגדר בפשטות כשלילת עצמו. זוהי הגדרה מעגלית, ולכן אינה תקפה. למשפטו של השקרן פשוט אין ערך אמת, הוא אינו אמיתי ואינו שקרי.
גֶדֶל בנה פרדוקס משל עצמו. הוא לקח טענה דומה לטענה של השקרן, כשההבדל הוא שהטענה שלו אינה מתייחסת לערך האמת של עצמה, אלא לאפשרות ההוכחה שלה. הפסוק של גדל הוא זה:
טענה זאת אינה ניתנת להוכחה.
חישבו: אם הטענה ניתנת להוכחה, כי אז היא נכונה, משום שמה שניתן להוכחה הוא נכון. אבל על פי תוכנה, אם היא נכונה, כי אז היא אינה ניתנת להוכחה. מה הראינו עד כה? שאם הטענה ניתנת להוכחה, היא אינה ניתנת להוכחה, כלומר מתקבלת סתירה. משמעות הדבר היא שהטענה אינה יכולה להיות ניתנת להוכחה (לולא כן הייתה מתעוררת סתירה). אבל ראו מה הראינו במשפט האחרון: הוכחנו שהטענה אינה ניתנת להוכחה, שעל פי תוכנה של הטענה משמעו שהיא נכונה! כלומר,למעשה, הוכחנו את הטענה! אם כך, בעוד שקודם הוכחנו שהטענה אינה ניתנת להוכחה, כרגע מצאנו לה הוכחה! זוהי סתירה.
הגענו כאן לסתירה, משום שהסתכלנו בטענה כשהיא מנוסחת במילים. הפרדוקס הזה מעודן יותר מאשר פרדוקס השקרן, והמעגליות החבויה בו אינה פשוטה כל כך (רמז: הבעיה היא בהנחה ש"מה שניתן להוכיח הוא נכון", שאם משתמשים בה לצורכי הוכחות היא הופכת להיות מוגדרת מעגלית, אבל לא ניכנס לכך כאן). גדל, לעומת זאת, לא הגיע לסתירה. את הטענה שלו הוא ניסח לא במילים אלא כנוסחה שמדברת על מספרים – הישג יוצא דופן בפני עצמו. בלבוש של נוסחה, הפסוק של גדל אינו מביא לסתירה, אלא למשפט אי השלמוּת. כשהוא מנוסח כטענה על מספרים, הפסוק אינו ניתן להוכחה וגם שלילתו אינה ניתנת להוכחה. הדבר מוכיח שתורת המספרים אינה שלמה. יש נוסחה שלגביה תורת המספרים אינה יודעת להכריע, באמצעות הוכחה, אם היא נכונה או לא.
[1]. גדל הוכיח בגיל 24 את מה שנחשב ל"משפט החשוב ביותר של המאה העשרים" – שמערכת אקסיומות "סבירה" לתורת המספרים אינה יכולה להוכיח את כל הטענות הנכונות במספרים הטבעיים. ב-1939 עבר לפרינסטון, בעקבות כיבוש אוסטריה בידי הנאצים. מאז ועד מותו נרשמו לזכותו רק שתי עבודות בעלות חשיבות. הוא היה כל ימיו חשדן ומסוגף, וסופו היה טרגי – הוא מת מרעב, לאחר שאשתו אושפזה בבית חולים והוא סירב לאכול מזון שלא הוכן בידיה.
חידות
דניאל לובזנס
דבר העורך: שמחתי כשהוצע לי לערוך את מדור החידות בנטגר. מאז ילדותי אהבתי לפתור חידות כאלו, למצוא פתרון, ואח"כ לגלות כי קיימים פתרונות אחרים, מעניינים ויפים. החידות מכוונות לתלמידות ותלמידים בכיתות הגבוהות בבתי הספר, אך גם צעירים יותר יכולים לנסות. החידות לא ידרשו ידע מתמטי מורכב או מושגים שאינם ידועים לתלמידי בתי הספר.
לחידות המוצגות בגיליון זה יפורסמו פתרונות בגיליון הבא. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 24.12.14, אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1– היכן המטבעות המזויפות?
מטבע של 10 שקלים משקלו 7 גרם, קיימים גם מטבעות מזויפים שמשקלם 6 גרם. יש 9 ערמות, בכל אחת 9 מטבעות של 10 שקלים. 8 ערמות מכילות מטבעות תקניים, וערמה אחת מורכבת כולה ממטבעות מזויפים. לרשותכם מאזניים מדויקים (דיוק של 0.1 גר'). מהו המספר המינימלי של שקילות הנדרשות לאיתור ערמת המטבעות המזויפים? (בכל שקילה נתן להניח על המאזניים מספר כל שהוא של מטבעות).
חזרו על החידה, כשהפעם יש 9 ערמות ובכל אחת מהן רק 3 מטבעות.
חידה 2- הקוסם
"קוסם" מודיע כי הוא יכול לנחש מספרים בני 3 ספרות שנחשוב עליהם. בכל זאת הוא מבקש רמז. להלן הוראותיו ליצירת הרמז: קחו את 3 הספרות של המספר שחשבתם עליו – סדרו אותם ב 5 הסידורים האפשריים השונים מהמספר המקורי (לסידור 3 ספרות יש 6 תמורות – אחת מהן של המספר המקורי, אם יש 2 או 3 ספרות שוות יש להשתמש בכל 5 התמורות שחלקן יהיו זהות למספר המקורי). את 5 המספרים בני 3 הספרות סכמו, וכרמז מסרו את סכומם ל"קוסם".
הראו כי מהרמז, המחושב בצורה הנזכרת לעיל, ניתן למצוא את המספר המקורי. מצאו שיטה שבה ה"קוסם" יוכל לחשב מהרמז את המספר המקורי בלי להתאמץ יותר מדי, רצוי בלי סיוע של מחשב או מחשבון.
חידה 3 - ניסור קוביה
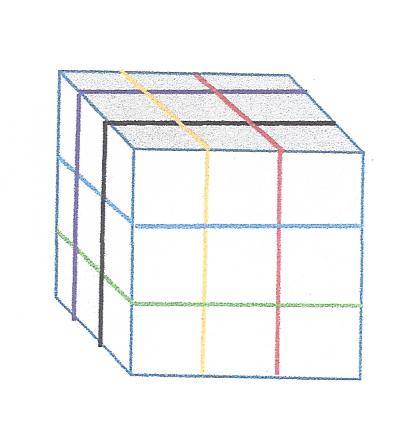
רוצים לחלק קובייה ל 27 קוביות שוות, ניתן לעשות זאת ע"י 6 קווי ניסור כמתואר בתרשים.
האם ניתן לעשות זאת בפחות צעדי ניסור? למשל ע"י הצבת החלקים המנוסרים בצורה שונה.
חיזרו על הבעיה למקרה בו רוצים לחלק את הקובייה ל 64 חלקים ( חלוקה ל 4 בכל כיוון) האם ניתן לעשות זאת בפחות מ 9 צעדים?
חידה 4 - החשמלאי במגדל
במגדל גבוה מועבר כבל חשמל ובו n גידים (כל אחד מכיל חוט מוליך מבודד). כל הגידים זהים לגמרי. חשמלאי צריך לסמן את הגידים בכל קצה במספרים 1,2,3……….n כך שכל גיד יקבל מספר יחיד שיופיע בשני קצותיו.
לצורך איתור הגידים החשמלאי יכול לחבר ביניהם כל מספר של מוליכים בצד אחד (בקומת הקרקע, או על גג המגדל) ואח"כ לטפס לצד השני ושם למצוא אלו מהגידים מחוברים חשמלית ביניהם, זאת ע"י מכשור פשוט הכולל סוללה ונורה. (שימו לב: אין ברשות החשמלאי מכשור מתקדם יותר המאפשר למשל למדוד התנגדות חשמלית, הניחו שלמרות שהמגדל גבוהה התנגדות החוטים אפסית והחשמלאי לא יוכל להבחין אם מעגל מוליך מורכב מחוט בודד או מספר חוטים מחוברים במקביל או בטור). החשמלאי יכול לעשות כל מספר חיבורים רצוי בהימצאו באחד הצדדים, ולבדוק רציפות חשמלית בין כל 2 חוטים, עיקר הקושי הוא הטיפוס במאתיים המדרגות מקומת הקרקע ועד הגג. החשמלאי מתחיל בעבודתו בקומת הקרקע.
הבעיה: מהו המספר המינימלי של עליות וירידות שעל החשמלאי לבצע כדי לסיים את מלאכתו?
תנו את דעתכם לכך שעבור n=1, הבעיה טריוויאלית – אין צורך לעשות כלום. עבור n=2 , אין כל דרך לבצע את העבודה. ואילו עבור n=3, ניתן לבצע את העבודה בעליה אחת וירידה אחת בצורה הבאה: החשמלאי מסמן את החוטים בקומת הקרקע באותיות A,B,C ומחבר את הקצוות B ו C . עולה לקומת הגג. שם ב 3 מדידות חשמליות הוא מוצא זוג אחד של חוטים המחוברים חשמלית ומסמן אותם במספרים 2,3 את החוט הנוסף (שאינו מחובר חשמלית לאף חוט אחר) מסמן ב- 1. החשמלאי מחבר זה לזה את החוטים 1 ו-2. יורד לקומת הכניסה. מסמן את A במס' 1 ובודק למי הוא מחובר חשמלית, מסמן את החוט שמחובר אליו ב- 2 ואת הנותר ב-3. החשמלאי מסיים כך את מלאכתו בעליה אחת וירידה אחת.