נטגר גליון 11

דבר העורך

רון אהרוני

מה פירוש ש-$latex {\pi = 3.14159\ldots}$? פירוש הדבר הוא ש$latex {\pi}$ הוא סכום אינסופי: $latex {3+0.1+0.04+0.001+0.0005+0.00009+\ldots}$. הרעיון הזה, שנראה מוזר לכאורה, שסכום של אינסוף מספרים יכול להיות מספר סופי, הוא רעיון בסיסי ביותר במתמטיקה - הנה, כפי שאתם רואים, הייצוג העשרוני של מספרים לא רציונליים מבוסס עליו. אנה ליזהטוב חוזרת ומספרת על הרעיון הזה, שמקורו עוד בימי היוונים הקדמונים.

אליהו לוי גם הוא חוזר אלינו, עם מאמר יפה על תכונות ייחודיות של שלושה מספרים.

במדור "דמות מתמטית" מספרים אלכסנדר קמרסקי ואני על אחת הדמויות המרתקות ביותר של המתמטיקה של המאה העשרים, הצרפתי אלכסנדר גרותנדיק. גרותנדיק, שחי חיים סוערים גם מחוץ לעולם המתמטיקה, נפטר לפני זמן לא רב וזהו מאמר לזכרו.

וכרגיל, יש מדור חידות, עם דני לובזנס.

בהנאה!

אינסוף מספרים שסכומם סופי

אנה ליזהטוב

את הפילוסוף היווני זֶנוֹן מאֶלֵיאָה (425-490 לפנה"ס) הטרידו שאלות בדבר היחס בין הרגעי והכללי. אלפיים שנים אחריו יעסקו מתמטיקאים באותן שאלות וימציאו בעקבות זאת את החשבון הדיפרנציאלי. אבל זנון, שלא הכיר את המושגים הנחוצים, היה סבור שהגיע לסתירות. המפורסמת ביניהן היא "פרדוקס אכילס והצב". במקור מדבר הפרדוקס על תחרות ריצה בין אכילס לבין צב, אבל כדי לא לחזור על הנוסח המוכר והנדוש, אכתוב את הפרדוקס בצורה מעט שונה מן המקובל, כתחרות בין שני מחוגי השעון. השאלה היא זו:

מחוגי השעון נפגשים בשעה $latex {12}$. באיזו שעה ייפגשו בפעם הבאה?

הפרדוקס של זנון אומר שהדבר לא יקרה אף פעם. זהו אבסורד, אבל לזנון הייתה "הוכחה" לכך, והרי היא לפניכם. בשעה $latex {1}$ בדיוק משיג המחוג הקטן את הגדול, משום שהוא מצביע על $latex {1}$ ואילו המחוג הגדול מצביע על $latex {12}$. עד שיגיע המחוג הגדול ל-$latex {1}$, יתקדם המחוג הקטן מעט. למעשה, אנחנו יודעים בדיוק כמה –$latex {\frac{1}{12}}$  של שעה, משום שמהירותו היא $latex {\frac{1}{12}}$ ממהירות המחוג הגדול, והמחוג הגדול התקדם שעה אחת, מ-$latex {12}$ ל-$latex {1}$. המחוג הקטן מצביע עתה על השעה $latex {1\frac{1}{12}}$ ($latex {1}$ ו-$latex {5}$ דקות), והמחוג הגדול צריך להגיע גם לשעה זו. אבל עד שיעשה זאת, יתקדם המחוג הקטן עוד קצת. למעשה, אנחנו יודעים בדיוק כמה: פי $latex {12}$ פחות מן המחוג הגדול, כלומר $latex {\frac{1}{12*12} = \frac{1}{144}}$ של שעה. המחוג הגדול צריך להגיע לאותה שעה, ובינתיים יתקדם המחוג הקטן עוד מעט, $latex {\frac{1}{12*144} = \frac{1}{1728}}$ של שעה. וכך יימשכו הדברים: כל פעם שהמחוג הגדול יגיע למקום שבו היה קודם לכן המחוג הקטן, המחוג הקטן יתקדם בינתיים עוד מעט. נראה אם כן שהמחוג הגדול לעולם לא יוכל להדביק את המחוג הקטן! תמיד יהיה ביניהם פער כלשהו, אף אם הוא קטן והולך. בפרדוקס המקורי, שבו כאמור אכילס מתחרה בריצה עם צב, אכילס נותן לצב "פור" כלשהו. על פי אותו נימוק בדיוק, אכילס לא יוכל לעולם להשיג את הצב, משום שבכל פעם שיגיע למקום שבו היה הצב קודם לכן, הצב יתקדם בינתיים, אף אם מעט. אלא שאנו יודעים כמובן שהמחוג הגדול ישיג את הקטן, ואכילס ישיג די מהר את הצב, שפירושו שהוכחתו של זנון מוטעה. אבל היכן הטעות?

לפני שנשיב על כך, נשאל את עצמנו: באיזו שעה בדיוק נפגשים המחוגים? אפשר לכתוב משוואה, ולפתור אותה. אבל יש דרך יפה והרבה יותר פשוטה לעשות זאת. במשך $latex {12}$ שעות נפגשים שני המחוגים בדיוק $latex {11}$ פעמים: כל שעה שלמה, ועוד קצת; פרט לשעה $latex {11}$ וקצת, משום שאז הפגישה היא כבר ב-$latex {12}$, ולא ב"$latex {11}$ וקצת". עתה יש לשים לב לכך שהזמן החולף בין כל שתי פגישות של המחוגים הוא קבוע. דרך קלה לראות זאת היא למחוק את המספרים מן השעון, ולסובב אותו כך שבזמן פגישת המחוגים נראה כאילו שני המחוגים מצביעים על השעה $latex {12}$: ברור עתה שעד לפגישה הבאה יעבור בדיוק אותו זמן כפי שעבר בין השעה $latex {12}$ לבין המפגש הבא של המחוגים. לפיכך $latex {12}$ שעות היום מתחלקות ל-$latex {11}$ פרקי זמן שווים, שעוברים בין הפגישות של המחוגים. לכן בין כל שתי פגישות חולפים $latex {\frac{12}{11}}$ ($latex {12}$ חלקי $latex {11}$) של שעה. הפגישה הראשונה אחרי $latex {12}$ תהיה אם כן בשעה $latex {\frac{12}{11}}$, כלומר $latex {1\frac{1}{11}}$, שהוא מעט לפני $latex {1}$ ו-$latex {6}$ דקות.

היכן טעה זנון? עד מקום מסוים טיעונו נכון, אלא שהוא טעה במסקנה. הוא פירק את פרק הזמן עד לפגישה הבאה של המחוגים לאינסוף חלקים. סכומם של אינסוף פרקי הזמן האלו (בשעות) הוא $latex {1 + \frac{1}{12}+ \frac{1}{144}+ \frac{1}{1728}+ \dots}$. זהו "טור אינסופי", כלומר סכום של אינסוף איברים. טענתו של זנון הייתה שמכיוון שבסכום הזה יש אינסוף איברים, הסכום הוא אינסופי, כלומר הזמן שיעבור עד לפגישה הבאה הוא אינסופי. אבל זוהי טעות. סכום של אינסוף מספרים יכול להיות סופי, בתנאי שהמספרים קטֵנים בקצב מספיק מהיר. זהו אכן מה שקורה כאן: כל מספר קטן מקודמו פי $latex {12}$. טור כזה נקרא כזכור "טור גיאומטרי, עם מנה $latex {\frac{1}{12}}$" (פגשנו בו בפרק "פינג-פונג מתמטי"). וכל טור גיאומטרי עם מנה קטנה מ-$latex {1}$ מתכנס לסכום סופי. הדוגמה הקלאסית לכך היא הטור הגיאומטרי עם מנה $latex {\frac{1}{2}}$, כלומר טור שבו כל איבר קטן מקודמו פי $latex {2}$: $latex {1 + \frac{1}{2}+ \frac{1}{4}+ \frac{1}{8}+ \dots}$. סכום הטור הזה הוא $latex {2}$ (עובדה שגם עליה נרמז בפרק "פינג-פונג מתמטי"). כדי לראות זאת, שימו לב שמרחקו של $latex {1}$ מ-$latex {2}$ הוא $latex {1}$; מרחקו של$latex {1 +\frac{1}{2}}$  מ-$latex {2}$ הוא $latex {\frac{1}{2}}$; מרחקו של $latex {1 + \frac{1}{2}+ \frac{1}{4}}$ מ-$latex {2}$ הוא $latex {\frac{1}{4}}$. הוספת כל איבר בטור מקטינה את המרחק מ-$latex {2}$ פי $latex {2}$. לכן הסכומים החלקיים של הטור שואפים ל-$latex {2}$. ה"סכומים החלקיים" הם סכומי האיברים הראשונים – במקרה זה הסכום החלקי הראשון הוא $latex {1}$, הסכום החלקי השני הוא $latex {1 + \frac{1}{2}}$, הסכום החלקי השלישי הוא $latex {1 + \frac{1}{2}+ \frac{1}{4}}$, וכו'.

ואכן, לא קשה להוכיח שאם $latex {q}$ הוא מספר חיובי קטן מ-$latex {1}$, הטור הגיאומטרי האינסופי $latex {1 + q + q^2 + q^3  + \dots}$ מתכנס למספר סופי. איזה מספר? זאת אפשר לחשב בדרך שננקטה בפרק "הספר בשמיים". נסמן את הסכום $latex {1 + q + q^2 + q^3  + \dots}$ ב-$latex {S}$. נכפול כל איבר בסכום ב-$latex {q}$, ונקבל $latex {qS = q + q^2 + q^3 + q^4 +\dots}$. אבל הביטוי הזה דומה להפליא לטור המקורי, שסכומו  $latex {S}$– ההבדל היחיד הוא היעדרו של המספר $latex {1}$ בהתחלה. כלומר, $latex {qS = S-1}$. בהעברת אגפים נקבל: $latex {S(1-q) = 1}$, ובהעברת אגפים נוספת נקבל: $latex {S = \frac{1}{1-q}}$. למשל, אם $latex {q = \frac{1}{2}}$, שעבורו הטור הוא $latex {1 + \frac{1}{2}+ \frac{1}{4} +\frac{1}{8}+ \dots}$, נקבל: $latex {S = \frac{1}{1-\frac{1}{2}} = 2}$, כפי שגילינו קודם. במקרה של מחוגי השעון, המחוגים ייפגשו אחרי $latex {1 + \frac{1}{12}+ \frac{1}{144}+ \frac{1}{1728}+ \dots}$ שעה, שעל פי הנוסחה (כאשר מציבים $latex {q = \frac{1}{12}}$), שווה ל: $latex { \frac{1}{1-\frac{1}{12}} = \frac{12}{11}}$, כפי שמצאנו קודם.

איברים ששואפים ל-0, וסכומם בכל זאת אינסופי

דוגמת הטור הגיאומטרי מעוררת את השאלה ההפוכה: האם תמיד כאשר איברי הטור שואפים ל-$latex {0}$ סכום הטור הוא סופי? התשובה היא לא, והדוגמה הפשוטה ביותר לכך היא זו: $latex {1 + \frac{1}{2}+ \frac{1}{2}+ \frac{1}{3}+ \frac{1}{3}+ \frac{1}{3}+ \frac{1}{4}+ \frac{1}{4}+ \frac{1}{4}+ \frac{1}{4} + \dots}$ (עתה יבואו $latex {5}$ פעמים $latex {\frac{1}{5}}$). האיברים שואפים ל-$latex {0}$, אבל שני חצאים הם $latex {1}$, ושלושה שלישים הם $latex {1}$, וארבעה רבעים הם $latex {1}$ – אנו מסכמים כאן אינסוף פעמים $latex {1}$, שפירושו שהסכומים החלקיים של הטור ("סכום חלקי" הוא הסכום המתקבל כשעוצרים בשלב סופי כלשהו) שואפים לאינסוף, כלומר סכום הטור הוא אינסופי.

הדוגמה הבאה מתוחכמת יותר, וגם חשובה יותר, משום שהיא מופיעה בהרבה הקשרים. זהו הטור $latex {1 + \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4}+ \dots}$, שנקרא ה"טור ההרמוני". איבריו שואפים ל-$latex {0}$, אבל סכומו אינסופי, שפירושו שהסכומים החלקיים שלו שואפים לאינסוף. כדי להראות זאת, נפריד את הסכום בצורה הבאה:

$latex {1 + \frac{1}{2}+ (\frac{1}{3}+ \frac{1}{4})+( \frac{1}{5}+ \frac{1}{6}+ \frac{1}{7}+ \frac{1}{8})+( \frac{1}{9}+ \frac{1}{10} + \dots + \frac{1}{16})+\dots}$

בזוג הסוגריים הראשון יש $latex {2}$ מספרים שכל אחד מהם הוא לפחות $latex {\frac{1}{4}}$ ,לכן סכומם גדול מ-$latex {2}$ פעמים $latex {\frac{1}{4}}$, שהוא $latex {\frac{1}{2}}$; בזוג הסוגריים השני יש $latex {4}$ מספרים שכל אחד מהם הוא לפחות $latex {\frac{1}{8}}$, ולכן סכומם גדול מ-$latex {4}$ פעמים $latex {\frac{1}{8}}$, שהוא $latex {\frac{1}{2}}$; בזוג הסוגריים השלישי יש $latex {8}$ מספרים, שכל אחד מהם הוא לפחות $latex {\frac{1}{16}}$, ולכן סכומם גדול מ-$latex {8}$ פעמים $latex {\frac{1}{16}}$, שהוא $latex {\frac{1}{2}}$. בכל זוג סוגריים סכום האיברים גדול מ-$latex {\frac{1}{2}}$, ומכיוון שיש אינסוף זוגות סוגריים, סכום הטור הוא לפחות "אינסוף פעמים $latex {\frac{1}{2}}$", שהוא אינסופי. הפירוש המדויק הוא, כאמור, שהסכומים החלקיים הולכים ושואפים לאינסוף.

רעיון משום מקום

אחד המרצים שלי באוניברסיטה הסביר לנו פעם ש"מושג מתמטי הוא טוב אם קיים משפט שהמושג אינו מופיע לא בהנחה ולא במסקנה שלו, אבל הוא מופיע בהוכחה שלו". במילים אחרות, מושג הוא טוב אם הוא מופיע "משום מקום", כדי להאיר את הדברים באור חדש ולגלות בהם סדר לא צפוי. זהו גם אחד הקריטריונים המובהקים ליופי. בפתרון יפה יש תמיד רעיון שאינך מבין מהיכן הגיע; רעיון שלא היה כלול בעולם המושגים של הבעיה, ולא היה נחוץ לניסוחה, אבל הוא חושף בה סדר חדש.

בגיאומטריה יש סוג מיוחד של "רעיון משום מקום": בניות עזר. קו או מעגל שלא הוזכרו בבעיה נוספים לציור, ומאותו רגע הדברים מתבהרים. כאילו ניסינו לטפס על חומה גבוהה, ומישהו בא והוסיף מדרגה, והטיפוס הופך לפתע קל. דוגמה ידועה היא ההוכחה שסכום הזוויות במשולש הוא $latex {180}$ מעלות. לשם כך מעבירים קו מקביל לאחת מצלעות המשולש, דרך הקדקוד הנגדי לה, הנה כך:

liza

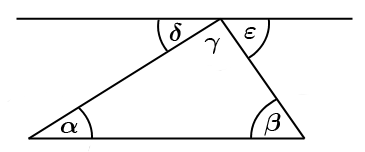
ועתה – הזווית $latex {\alpha}$ שווה לזווית $latex {\delta}$ , ואילו הזווית $latex {\beta}$ שווה לזווית $latex {\varepsilon}$ . מכיוון ש-$latex {\delta}$,$latex {\varepsilon}$  ו- $latex {\gamma}$ נמצאות על ישר אחד, סכומן $latex {180}$ מעלות, ועל כן גם סכומן של $latex {\alpha , \beta}$,  ו-$latex {\gamma}$ הוא $latex {180}$ מעלות.

הוכחה לקיומם של אינסוף מספרים ראשוניים

העובדה שקיימים אינסוף מספרים ראשוניים מופיעה בספרו של אוקלידס יסודות, אף כי ייתכן שהייתה ידועה לפני כן. הוכחתו המקורית של אוקלידס יפה כשלעצמה, אבל לא אחזור עליה כאן (היא מופיעה, למשל, בספרי חשבון להורים). במקום זאת אביא הוכחה אחרת, של אוילר, יפה לא פחות.

נניח, לשם שלילה, שיש רק מספר סופי של מספרים ראשוניים, נאמר $latex {2,3,5,7,…,p}$. כלומר –$latex {p}$  הוא המספר הראשוני הגדול ביותר. נתבונן במכפלה הבאה: $latex {\frac{2}{2-1}*\frac{3}{3-1}*\frac{5}{5-1}*\dots*\frac{p}{p-1}}$, שבה מופיעים במונים כל המספרים הראשוניים, ובמכנים המספרים הראשוניים, פחות $latex {1}$. מדוע להסתכל דווקא במכפלה הזאת? היופי הוא בכך שבינתיים אין זה ברור. זהו ה"רעיון משום מקום", קפיצת המחשבה הלא צפויה. מכיוון שזוהי מכפלה של מספר סופי של מספרים, תוצאתה היא מספר סופי. אנו נקבל סתירה (סתירה שתראה שההנחה שיש רק מספר סופי של מספרים ראשוניים היא מוטעית) מכך שנראה שהמספר הזה שווה לסכום הטור ההרמוני, $latex {1 + \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4}+ \dots}$, שהוא כזכור אינסופי.

ניזכר בנוסחה שלמדנו בפרק הקודם, לסכום של טור גיאומטרי אינסופי: למספר כלשהו $latex {q}$ הקטן בערכו המוחלט מ-$latex {1}$, מתקיים:$latex {1+q+q^2+q^3+\dots=\frac{1}{1-q}}$ . ניקח את האיבר הראשון במכפלה האמורה,$latex {\frac{2}{2-1}}$  . כמובן, הוא שווה ל-$latex {2}$, אבל נתבונן בו מעט אחרת. נחלק מונה ומכנה ב-$latex {2}$, ונקבל שהביטוי שווה ל-$latex {\frac{1}{1-\frac{1}{2}}}$ . על פי הנוסחה לסכום הטור הגיאומטרי האינסופי, כאשר מציבים בו $latex {q=\frac{1}{2}}$ , מספר זה שווה ל: $latex {1+\frac{1}{2}+(\frac{1}{2})^2+(\frac{1}{2})^3+\dots}$. בדומה, האיבר השני במכפלה, $latex {\frac{3}{3-1}}$, שווה ל: $latex {1+\frac{1}{3}+(\frac{1}{3})^2+(\frac{1}{3})^3+\dots}$, והאיבר השלישי ל: $latex {1+\frac{1}{5}+(\frac{1}{5})^2+(\frac{1}{5})^3+\dots}$, וכו'.

המכפלה שווה אפוא למכפלת כל הביטויים האלו:

$latex {(1+\frac{1}{2}+(\frac{1}{2})^2+(\frac{1}{2})^3+\dots)*(1+\frac{1}{3}+(\frac{1}{3})^2+(\frac{1}{3})^3+\dots)*\dots*(1+\frac{1}{p}+(\frac{1}{p})^2+(\frac{1}{p})^3+\dots)}$

(כאשר $latex {p}$ הוא כאמור המספר שאנו מניחים שהוא הראשוני הגדול ביותר). כשנפתח את הסוגריים במכפלה הזאת נקבל סכום של מכפלות. מכפלה טיפוסית ביניהן תהיה, למשל: $latex {\frac{1}{2^3}*\frac{1}{3}*\frac{1}{7^4}}$. כלומר כל מכפלה היא שבר שבו יש $latex {1}$ במונה, ומכפלה של חזקות של מספרים ראשוניים במכנה. אבל כל מספר טבעי ניתן לביטוי כמכפלת חזקות של מספרים ראשוניים! למשל, $latex {600 = 2^3*3*5^2}$. משום כך לכל מספר $latex {n}$ יופיע השבר $latex {\frac{1}{n}}$ כאחד המחוברים בסכום. (למשל, $latex {\frac{1}{600}}$ יופיע כ: $latex {\frac{1}{2^3}*\frac{1}{3}*\frac{1}{5^2}}$). יוצא שפתיחת הסוגריים של המכפלה נותנת את סכום כל המספרים מהצורה $latex {\frac{1}{n}}$, כלומר המכפלה שווה ל:$latex {1 + \frac{1}{2}+ \frac{1}{3}+ \frac{1}{4}+ \dots}$ . זהו סכום הטור ההרמוני, והוא כזכור אינסופי. כך הגענו לסתירה המובטחת – מכפלה סופית, השווה לסכום אינסופי.

אני מודה שזוהי הוכחה לא לגמרי פשוטה. אבל נראה לי שהרעיון הלא צפוי בה, של הסתכלות במכפלה, שווה בטירחה שבהבנתה.

מספרים "לא כמו כולם"

אליהו לוי

בשלושת חלקי מאמר זה נפנה את הזרקור אל שלושה מספרים בעלי תכונה "מופלאה" המבדילה אותם מן השאר.

על תכונה מופלאה של המספר $latex {30}$

בחלק הראשון נלך בעקבות פיסקה בספר: "מבוא למתימטיקה" מאת פרופ' אברהם הלוי פרנקל, ( כרך ראשון: המספר והפונקציה, עמ' 57-59), שיצא בשנת 1942. ( הוצאת מסדה, תל-אביב, הודפס שוב ב 1954).

פרופ' אברהם הלוי פרנקל היה מראשי הפקולטה למתמטיקה באוניברסיטה העברית בשלושים שנותיה הראשונות ( ראו במאמר: "אדמונד לנדאו: סיפור עם הוכחה" בגליון מרץ $latex {2014}$ של נטגר). הספר "מבוא למתמטיקה" היה מפעל חלוצי שלו, אולי הספר הראשון בעברית שנועד להסביר קצת "בעיות ושיטות מן המתמטיקה החדישה" לקהל התלמידים והמבוגרים המתעניינים ( שיכולים ללמוד הרבה מספר זה גם היום, למרות שקשה קצת להשיגו ושמה שנחשב ל"מתמטיקה חדישה" השתנה קצת בעשרות השנים שעברו)$latex {^1}$

נביא את דברי פרופ' פרנקל בסיפרו, כמעט בלשונו הוא:

יסמן $latex {n}$ אחד משמונת המספרים: $latex {3}$, $latex {4}$, $latex {6}$, $latex {8}$, $latex {12}$, $latex {18}$, $latex {24}$, $latex {30}$. לכל $latex {n}$ כזה ישנה התכונה: כל המספרים הקטנים מ $latex {n}$ וזרים ל $latex {n}$ הם או $latex {1}$ או ראשוניים. נכנה לשם קיצור את התכונה הזאת של מספר $latex {n}$ בשם $latex {T}$. מובן שלא לכל מספר מגיעה התכונה $latex {T}$; למשל לא למספרים $latex {10}$, $latex {28}$, $latex {36}$. כי הלא $latex {9}$ זר ל $latex {10}$ ול $latex {28}$, $latex {25}$ זר ל $latex {36}$, ועם זאת $latex {9}$ ו $latex {25}$ אינם מספרים ראשוניים. תכונתו המופלאה של המספר $latex {30}$ שברצוננו לעסוק בה היא: אין במציאות שום מספר למעלה מ $latex {30}$ שיש לו התכונה $latex {T}$. לשון אחר:

$latex {30}$ הינו המספר הגדול ביותר בעל התכונה $latex {T}$.

כדי להתקרב אל הוכחת המשפט הזה, נצא מעובדות פשוטות אלו: כל מספר בעל התכונה $latex {T}$ הגדול מ $latex {4}$, צריך על כל פנים להיות זוגי, מכיון שאחרת המספר $latex {4}$ ( שאינו ראשוני) זר לו. מתוך נימוק דומה צריך כל מספר בעל התכונה $latex {T}$, הגדול מ $latex {9}$, להתחלק ב $latex {3}$; כי אחרת יהיה $latex {9}$ זר לו. אם נצרף את שני התנאים האלה, יוצא כי כל מספר בעל התכונה $latex {T}$ הגדול מ $latex {9}$, מתחלק ב $latex {2\cdot3=6}$. כמו כן צריכים אחרי $latex {25}$ המספרים בעלי התכונה $latex {T}$ להתחלק ב $latex {2\cdot3\cdot5=30}$, אחרי $latex {49}$ להתחלק ב $latex {2\cdot3\cdot5\cdot7=210}$, אחרי $latex {121}$ ב $latex {2\cdot3\cdot5\cdot7\cdot11=2310}$, וכן הלאה. לפי זה יבואו בחשבון בשביל התכונה $latex {T}$:

בין $latex {4}$ ל $latex {9}$ המספרים $latex { 6,8}$;
בין $latex {9}$ ל $latex {25}$ המספרים $latex {12, 18, 24}$;
בין $latex {25}$ ל $latex {49}$ המספר $latex {30}$;

בין $latex {49}$ ל $latex {121}$ לא יבוא בחשבון שום מספר, מפני שכבר המספר הטבעי הראשון המתחלק ב $latex {210}$ - הוא $latex {210}$ עצמו - גדול מ $latex {121}$. מפני אותו הנמוק אי-אפשר למספר בעל התכונה $latex {T}$ להימצא בין $latex {11^2=121}$ ל $latex {13^2=169}$, היות והמספר $latex {2310}$ הנהו גדול מ $latex {169}$. הסברה משדלת אותנו להאמין, שאם נלך כך הלאה, לא נפגוש לעולם עוד מספר שיהיה בעל התכונה $latex {T}$. מאידך גיסא אנו רואים מיד כי המספרים הרשומים לעיל ($latex {6}$, $latex {8}$, $latex {12}$, $latex {18}$, $latex {24}$, $latex {30}$) הנם באמת בעלי התכונה $latex {T}$. הוספנו עליהם את המספרים בעלי התכונה $latex {T}$ שאינם עולים על $latex {4}$, והם $latex {3}$, $latex {4}$.

לכן התכונה הזו של המספר $latex {30}$ תנבע מהטענה הבאה:

טענה 1 עבור כל ראשוני $latex {p\ge11}$, $latex {p^2}$ קטן ממכפלת הראשוניים הקטנים מ $latex {p}$.

נשווה זאת להוכחה הידועה של אוקלידס לכך שקיימים אינסוף מספרים ראשוניים, או, במלים אחרות: עבור קבוצה סופית $latex {\mathcal{P}}$ של ראשוניים, אפשר למצוא ראשוני שאינו ב $latex {\mathcal{P}}$. אוקלידס בונה את מכפלת כל אברי $latex {\mathcal{P}}$, שכמובן מתחלקת בכולם, ומכאן שמכפלה זו פחות $latex {1}$ לא מתחלקת באף אחד מהראשוניים ב $latex {\mathcal{P}}$, ואם ניקח גורם ראשוני שלה, הוא יהיה ראשוני שאינו ב $latex {\mathcal{P}}$, ושבנוסף לכך קטן ממכפלת אברי $latex {\mathcal{P}}$. כלומר: כל ראשוני $latex {p}$ קטן ממכפלת הראשוניים הקטנים ממנו. טענה 1, לה אנו זקוקים בשביל להוכיח את התכונה של המספר $latex {30}$, אומרת שהחל מ $latex {p=11}$ אפילו $latex {p^2}$ קטן ממכפלה זו. לשון אחרת, $latex {p}$ קטן גם מהשורש הריבועי של מכפלה זו.

כאשר בודקים את הערכים המספריים, רואים ש $latex {p}$ קטן בהרבה משורש זה. אלא שאפילו אם בדיקת מספר סופי ענק של דוגמאות מראה זאת, אין זה קל להוכיח שאם נעבור על כל אינסוף הראשוניים לא יהיו רווחים גדולים מדיי ביניהם. עם זאת, הוכיחו משפטים הרבה יותר חזקים מטענה 1, אבל הוכחות אלו משתמשות באמצעים מתמטיים "גבוהים" שרחוקים מרחק רב ממושגי החשבון הבסיסיים שבהם, בסופו של דבר, עוסקת הטענה עצמה. לעומת זאת לטענה 1, שהיא הרבה יותר חלשה מהם אבל יותר חזקה ממסקנתו של אוקלידס, יש הוכחה שאינה רחוקה בהרבה משיקולו של אוקלידס, אבל עם תחבולה יפה שמספקת לנו את $latex {p^2}$ במקום $latex {p}$. נביא הוכחה זו בנספח בסוף.

על תכונה מופלאה של המספר $latex {24}$

נעשה תרגיל קטן: נבדוק מהי השארית בחלוקה ל $latex {24}$ של ריבועי מספרים זרים ל $latex {24}$ ( כלומר שאינם מתחלקים ב $latex {2}$ וב $latex {3}$, לשון אחרת - נותנים שארית $latex {1}$ או $latex {5}$ בחלוקה ל $latex {6}$)

$latex \displaystyle \begin{array}{cccc} 1^2=1=0\cdot24+1,& 5^2=25=1\cdot24+1,\\& 7^2=49=2\cdot24+1,& 11^2=121=5\cdot24+1,\\ 13^2=169=7\cdot24+1,& 17^2=289=12\cdot24+1,\\& 19^2=361=15\cdot24+1,& 23^2=529=22\cdot24+1 \end{array} $

ריבועי כל המספרים שבדקנו נותנים שארית $latex {1}$!

ומכאן שכל ריבוע של מספר זר ל $latex {24}$ נותן שארית $latex {1}$ - די בכך שבדקנו את המספרים בשורה הראשונה $latex {1}$, $latex {5}$, $latex {7}$, $latex {11}$, כי כל מספר זר ל $latex {24}$ קונגרואנטי מודולו $latex {24}$ לאחד מ $latex {\pm1}$, $latex {\pm5}$, $latex {\pm7}$, $latex {\pm11}$ ומספרים קוגרואנטיים מודולו $latex {N}$ גם ריבועיהם קונגרואנטיים מודולו $latex {N}$! ( וריבועו של מספר שאינו זר ל $latex {24}$ לא יכול לתת שארית $latex {1}$ בחלוקה ל $latex {24}$) - הסבירו.

כלומר ל $latex {N=24}$ ישנה התכונה הבאה, שנסמנה ב $latex {\Pi}$: כל מספר זר ל $latex {N}$ ריבועו נותן שארית $latex {1}$ בחלוקה ל $latex {N}$.

בדיקה דומה לבדיקה לעיל מראה שכל המחלקים של $latex {24}$ הם בעלי התכונה $latex {\Pi}$.

מצד שני $latex {10}$, וכן $latex {30}$, אינם בעלי התכונה $latex {\Pi}$: $latex {7^2=49}$ נותן שארית $latex {9}$ בחלוקה ל $latex {10}$ ושארית $latex {19}$ בחלוקה ל $latex {30}$!

מתברר ש:

טענה 2: $latex {24}$ הוא המספר הגדול ביותר בעל התכונה $latex {\Pi}$. יתר על כן: המספרים בעלי התכונה $latex {\Pi}$ הם בדיוק המחלקים של $latex {24}$.

הוכחה:

על תכונה מופלאה של המספר $latex {e}$

בחלק השלישי "ציבור" המספרים לא יהיה קבוצת הטבעיים, אלא קבוצת הממשיים, ליתר דיוק קבוצת הממשיים $latex {a}$ הגדולים מ $latex {1}$. אם $latex {a}$ מספר כזה, ייתכן שקיים מספר אחר $latex {b>1, b\ne a}$ כך ש $latex {a^b=b^a}$. הדוגמה המפורסמת היא $latex {2^4=4^2}$. אבל כאן מתקיימת

טענה 3 עבור כל $latex {a>1}$ ממשי,פרט ל $latex {e}$, קיים מספר יחיד $latex {b>1, b\ne a}$ כך ש $latex {a^b=b^a}$. עבור $latex {e}$ לא קיים $latex {b}$ כזה.

הוכחה. כל מה שעלינו לעשות הוא להפריד את המשתנים במשוואה $latex {x^y=y^x}$, $latex {x,y>1}$, וזאת נעשה ע"י העלאת שני האגפים בחזקת $latex {1/(xy)}$. נקבל את המשוואה $latex {x^{1/x}=y^{1/y}}$, כלומר $latex {x}$ ו $latex {y}$ צריכים להיות שני מקומות בהם הפונקציה $latex {x^{1/x}}$ ב $latex {(1,\infty)}$ מקבלת אותו ערך. עלינו, אם כך, לחקור את הפונקציה הזאת. הנגזרת שלה היא

$latex \displaystyle \left(x^{1/x}\right)'=\left(e^{\ln x/x}\right)'=\left(\ln x/x\right)'x^{1/x}= \left((1-\ln x)/x^2\right)x^{1/x}$

מכאן שהפונקציה עולה עבור $latex {\ln x<1}$ כלומר $latex {x<e}$ ויורדת עבור $latex {\ln x>1}$ כלומר $latex {x>e}$. ב $latex {e}$ יש לה מקסימום. ברור שבכל האינטרוול $latex {(1,\infty)}$ הפונקציה גדולה מ $latex {1}$.

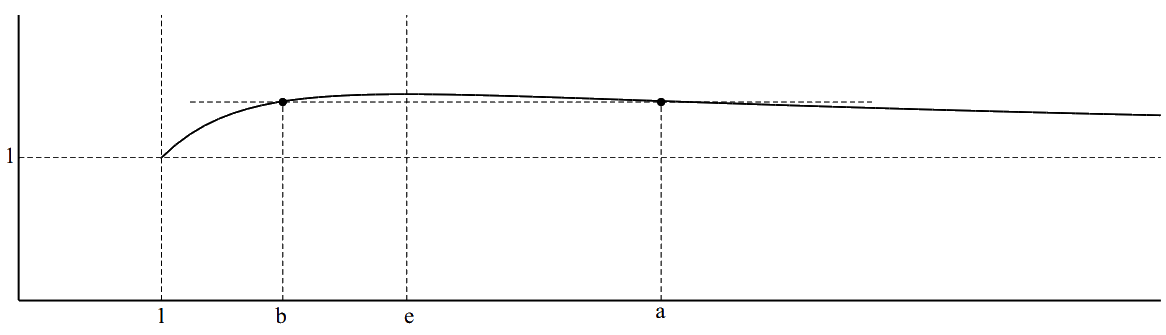
eliaho1

אם נראה כעת שכאשר $latex {x}$ שואף ל $latex {1}$ או $latex {\infty}$ הפונקציה שואפת ל $latex {1}$, אזי מצורת גרף הפונקציה ( וכמובן, ממשפט ערך הביניים של פונקציה רציפה) תנבע הטענה.

באשר לשאיפה ל $latex {1}$, הפונקציה מוגדרת ורציפה גם באינטרוול הסגור $latex {[1,\infty)}$ וערכה ב $latex {1}$ הוא $latex {1}$, ומכאן שהיא שואפת ל $latex {1}$ כאשר $latex {x\rightarrow1^+}$.

באשר למה שקורה כאשר $latex {x\rightarrow\infty}$, הפונקציה יורדת וברור שערכה גדול מ $latex {1}$. כדי להוכיח שהיא שואפת ל $latex {1}$ די להוכיח שערכיה על הסדרה $latex {x=4^n}$ שואפים ל $latex {1}$ כאשר $latex {n\rightarrow\infty}$. אבל

$latex \displaystyle \left(4^n\right)^{1/4^n}=4^{n/4^n}$

ו $latex {n/4^n\rightarrow0}$ כאשר $latex {n\rightarrow\infty}$, כי קודם כל $latex {n\le2^n}$, מאחר שבין $latex {2^n}$ המספרים $latex {1,2,3,\ldots,2^n}$ ישנן $latex {n}$ החזקות של שתיים $latex {2^1,2^2,\ldots,2^n}$, ומכאן יוצא $latex {n/4^n\le1/2^n}$. מ.ש.ל.

נספח: הוכחת טענה 1

את ההוכחה לטענה 1, המשתמשת רק בחשבון בסיסי, מצא סטודנט באוניברסיטת מינסטר בגרמניה, $latex {H. Bonse}$ בשנת $latex {1907}$ והיא מופיעה בספר של ראדמכר וטפליץ ובמאמר של צרמלו שהוזכרו בהערת השוליים לחלק הראשון לעיל.

נבנה את סדרת הראשוניים שלב שלב: נתחיל מחמשת הראשוניים הראשונים $latex {2,3,5,7,11}$ ובכל שלב נוסיף את הראשוני הבא. כך נקבל $latex {2,3,5,7,11,13}$, אחר כך $latex {2,3,5,7,11,13,17}$, וכו'.

אלא שבסידרת הראשוניים בכל שלב נסמן ראשוני מסויים. זה יהיה הראשוני הראשון בסדרה שהוא גדול ( ממש) ממספר אברי הסדרה שאינם לפניו ( כלומר הוא עצמו ואלה שאחריו).

נראה כיצד זה עובד: נתחיל בסדרה הראשונה $latex {2,3,5,7,11}$. $latex {2}$ לא טוב כי יש $latex {5}$ אברים לא לפניו. $latex {3}$ גם הוא לא טוב - יש לא לפניו $latex {4}$ אברים. $latex {5}$ טוב, כי יש לא לפניו $latex {3}$ אברים, ולכן נסמן אותו.

נעבור לסדרה הבאה $latex {2,3,5,7,11,13}$, בה צרפנו את $latex {13}$. ברור שהאיברים שלא היו טובים קודם לא יהיו טובים גם עכשיו. מה בדבר $latex {5}$? הוא עדיין טוב כי עכשיו יש $latex {4}$ איברים לא לפניו. לכן עדיין $latex {5}$ הוא המסומן.

אבל אחרי שהוספנו את $latex {17}$ יהיו $latex {5}$ אברים לא לפני $latex {5}$ - לא טוב. לכן עלינו לעבור ל $latex {7}$, יש $latex {4}$ אברים לא לפניו, ולכן הוא יהיה המסומן.

וכן הלאה.

שימו לב שכל מספר מסומן שומר על הסימון לפחות שני שלבים: בשלב האחרון ש $latex {p}$ סומן, היו $latex {p-1}$ אברים לא לפניו ( לכן הוא יאבד את הסימון בשלב הבא). בשלב הבא נסמן את הראשוני הבא $latex {p'}$, לא לפניו יהיו אז $latex {p-1}$ אברים, ומאחר ש $latex {p'\ge p+2}$ הוא יהיה טוב גם בשלב שאחרי זה.

כעת אני טוען:

טענת עזר: בכל שלב, נסמן ב $latex {P}$ את מכפלת כל הראשוניים בסדרה, ב $latex {P_0}$ את מכפלת הראשוניים שלפני הראשוני שסומן $latex {p}$, וב $latex {P_1=p\cdot P_0}$ את מכפלת הראשוניים שלא אחרי $latex {p}$. אז תמיד $latex {P_1}^2<P $.

ההוכחה באינדוקציה: בסדרה הראשונה $latex {P=(2\cdot3\cdot5)\cdot(7\cdot11)}$ $latex {P_1}^2=(2\cdot3\cdot5)^2 $ והטענה מתקבלת מכך ש $latex {2\cdot3\cdot5=30<77=7\cdot11}$.

ברור שבשלב בו לא משתנה הראשוני המסומן לא תתקלקל נכונות הטענה, כי $latex {P_1}$ לא משתנה ו $latex {P}$ גדל.

נתבונן כעת בשלב בו הסימון הוא ב $latex {p'}$ אבל בשלב הקודם הוא היה בראשוני הקודם לו $latex {p}$. כמו שראינו, יש בשלב זה $latex {p-1}$ אברים בסדרה לא לפני $latex {p'}$. נשווה את המצב כעת למצב שני שלבים קודם. מאחר שכמו שהראינו, $latex {p}$ שמר על הסימון לפחות שני שלבים, הוא היה זה שסומן שני שלבים קודם. לכן ההבדל בין שלב זה והשלב הקודם הוא ש $latex {P_1}$ גדל פי $latex {p'}$ ואז $latex {P_1}^2 $ גדל פי $latex {p'^2}$. לעומת זאת $latex {P}$ גדל פי מכפלת שני הראשוניים שנוספו בסוף הסדרה, ( שימו לב שהם $latex {p-3}$ ו $latex {p-2}$ מקומות אחרי $latex {p'}$, בוודאי גדולים מ $latex {p'}$) וזה יותר מ $latex {p'^2}$. מכאן שאם טענת העזר הייתה נכונה בשלב הקודם היא תישאר נכונה גם עכשיו.

בכך הוכחה טענת העזר.

לכן טענה 1 תוכח אם נראה שבכל שלב, הראשוני הראשון שאחרי כל אברי הסדרה קטן מ $latex {P_1}$.

לשם כך נתבונן בביטויים $latex {P_0-1, 2\cdot P_0-1,\ldots,p\cdot P_0-1}$ כאשר $latex {p}$ הוא הראשוני המסומן. ברור שכולם לא מתחלקים באף אחד מאברי הסדרה שלפני $latex {p}$ ( שנכללים במכפלה $latex {P_0}$). אני טוען שעבור כל ראשוני $latex {q}$ בסדרה לא לפני $latex {p}$ ( כלומר $latex {p}$ או אחריו), לכל היותר אחד מביטויים אלה מתחלק ב $latex {q}$. כי אילו היו שניים המתחלקים ב $latex {q}$, היה גם ההפרש ביניהם מתחלק ב $latex {q}$, אבל הפרש זה הוא מכפלת $latex {P_0}$ במספר קטן מ $latex {q}$, ולכן כל הגורמים הראשוניים של ההפרש קטנים מ $latex {q}$.

אבל יש לנו $latex {p}$ ביטויים, והעובדה ש $latex {p}$ סומן אומרת שמספר זה גדול ממספר ה $latex {q}$-ים שלא לפני $latex {p}$, וכאמור בכל $latex {q}$ מתחלק לכל היותר ביטוי אחד. לכן מקבלים שאחד הביטויים לפחות $latex {j\cdot P_0-1}$ לא מתחלק באף $latex {q}$ בסדרה שלא לפני $latex {p}$, וראינו שגם לא באלה שלפני $latex {p}$. כעת מסיימים את הטיעון כמו אצל אוקלידס: ביטוי זה קטן מ $latex {P_1}$, ולכן גם גורם ראשוני שלו, שכמו שמצאנו לא שייך לסדרה, קטן מ $latex {P_1}$, ומכאן שהראשוני הראשון שאחרי הסדרה קטן מ $latex {P_1}$, מ.ש.ל.

תרגילים

1. האם תוכלו להוכיח באותה צורה שבנספח שהחל מ $latex {p}$ ראשוני מסויים גם $latex {p^3}$ קטן ממכפלת הראשוניים הקטנים מ $latex {p}$?

רמז: הראו שממקום מסויים $latex {P_1}^3<P $ באינדוקציה על השלבים, ע"י השוואת שלב לשלב $latex {6}$ צעדים לפניו. בששה צעדים אלה יזוז הסימון לכל היותר שני מקומות ( מדוע?), ולכן $latex {P_1}^3 $ יוכפל בפחות ממה שיוכפל $latex {P}$.

מה בדבר $latex {p^4,p^5,\ldots}$?

2. נסדר את הראשוניים בסדרה עולה:

$latex \displaystyle p_1=2,\,p_2=3,\,p_3=5,\,p_4,\,p_5,\,p_6,\ldots$

הוכיחו שעבור כל $latex {n=1,2,\ldots}$ מתקיים:

$latex \displaystyle p_1\cdot p_2\cdot p_3\cdot\cdots\cdot p_n\ge p_{n+p_n-1}.$

הוכיחו שעבור כל $latex {n=3,4,\ldots}$ ולא להתחיל מ$latex {1}$ . עבור $latex {1}$ ו $latex {2}$ האי-שוויון לא נכון וגם ההוכחה נשברת. מ$latex {3}$ הוא נכון.

נסו להשתמש בנוסחה זו לתת צורה קצת אחרת להוכחה שבנספח.

3. תהיינה $latex {x_1,x_2,\ldots}$ ו $latex {y_1,y_2,\ldots}$ סדרות אינסופיות של מספרים ממשיים גדולים מ $latex {1}$, כך ש:

$latex \displaystyle x_n\ne y_n,\quad {x_n}^{y_n}={y_n}^{x_n}.$

וכך שההפרש בין $latex {x_n}$ ו $latex {y_n}$ שואף ל $latex {0}$ כאשר $latex {n\rightarrow\infty}$. ( היווכחו שקיימות סדרות כאלה!)

הוכיחו שלסדרה $latex {x_n}$ יש גבול $latex {L}$ כאשר $latex {n\rightarrow\infty}$ ( שיהיה כמובן גם הגבול של $latex {y_n}$). מהו? מיצאו את הגבול של

$latex \displaystyle \dfrac{y_n-L}{x_n-L}.$

$latex {^1}$בנושא התכונה של המספר $latex {30}$ פרופ' פרנקל הלך כנראה בעקבות הספר: $latex {Von Zahlen und Figuren}$ ( על מספרים וצורות) של הנס ראדמכר ואוטו טפליץ, ומאמר ידוע של צרמלו.

$latex {^2}$ במבט ראשון נראה שמשהו לא בסדר ב $latex {(*)}$: בשביל שקיום התכונה $latex {\Pi}$ יהיה שקול לקיום התכונות $latex {(*)}$ עבור כל $latex {p=p_i,m=m_i}$, $latex {i=1,\ldots,k}$, צריך בניסוח של $latex {(*)}$ לכתוב: "הריבוע של כל $latex {a}$ שאינו מתחלק באף אחד מ $latex {p_1,\ldots,p_k}$". אבל מ-משפט השאריות הסיני נובע ששני ניסוחים אלה שקולים. משפט השאריות הסיני אומר שעבור כל $latex {k}$ שאריות $latex {a_1\mod{p_1}^{m_1},\ldots,a_k\mod{p_k}^{m_k}}$ קיימת שארית $latex {a\mod N}$ כך ש $latex {a\equiv a_i\mod{p_i}^{m_i}}$ עבור כל $latex {i=1,\ldots,k}$. לכן ב $latex {(*)}$ נוכל להחליף את $latex {a}$ במספר שנותן אותה שארית כמו $latex {a}$ מודולו $latex {p^m}$ ושארית זרה ל $latex {p_j}$ מודולו ה $latex {p_j}^{m_j} $ האחרים.

אלכסנדר גרותנדיק - האיינשטיין של המתמטיקה

רון אהרוני ואלכסנדר קמרסקי

לאלברט איינשטיין לא היה שני בפיזיקה של המאה העשרים. הוא יצר את שתי התורות הגדולות ששלטו בפיזיקה לאורך כל המאה - תורת היחסות ותורת הקוואנטים. חשיבתו הפיזיקלית הייתה מופשטת יותר מכל מה שנודע לפניו. הוא פשוט "ראה" דברים.

האם יש דמות כזו גם במתמטיקה של המאה העשרים? מישהו שהפך את התפיסה של תורות שלמות? מועמד אחד בולט להיות במעמד הזה הוא המתמטיקאי הצרפתי אלכסנדר גרותנדיק $latex {(Alexander~~Grothendieck)}$. רבים רואים בו את המתמטיקאי הגדול של המאה העשרים, ויש אכן כאלו שקוראים לו ה"איינשטיין של המתמטיקה". גישותיו החדשות, והמופשטות לעילא, שינו את פניהן של תורת המספרים, ושל תחום שנקרא "גיאומטריה אלגברית". זהו התחום שחוקר את קבוצות הפתרונות של פולינומים בהרבה משתנים. בזכותו הגישות האלה ניתן היה לפתור בעיות שהיו פתוחות זמן רב. המאמר הזה הוא לזכרו: גרותנדיק נפטר לפני כחודשיים, ב-$latex {13}$ בנובמבר $latex {2014}$.

כסטודנט לתואר שני קיבלתי מן המנחה שלי ספרון, הדוקטורט של גרותנדיק, שנכתב בשנות ה-$latex {50}$ של המאה העשרים. התחום היה אנליזה פונקציונלית, שחוקרת את ההכללה של המרחב שאנחנו מכירים לממדים אינסופיים. המנחה שלי הסביר לי שבאותו זמן, יותר מעשרים שנים אחרי כתיבת הדוקטורט הזה, אנשי האנליזה הפונקציונלית עדיין קוראים אותו ודולים ממנו פנינים למחקריהם. הופתעתי מאוד אחר כך כשלמדתי שזה בכלל אינו התחום העיקרי של גרותנדיק: מייד אחרי הדוקטורט עבר לגיאומרטיה אלגברית, תחום שלכאורה אין לו הרבה קשר לאנליזה פונקציונלית. אבל מתברר שהוא לקח מן התחום הישן רעיונות רבים לתחום החדש.

חייו של גרותנדיק יכלו לשמש חומר לרומן מרתק גם ללא צידם המתמטי. הוא נולד לתוך זמנים קשים, במקום הלא נכון להורים ממוצא ואמונות לא נכונות. הוא נולד בברלין, ב-$latex {1928}$, לאב יהודי שהיגר לגרמניה מרוסיה, ולאם פרוטסטנטית. שני הוריו היו אנרכיסטים פעילים, וב-$latex {1933}$, כשהיטלר עלה לשלטון, כם הפקידו אותו בידי כומר שהסכים לגדלו ללא תשלום, ונסעו לצרפת ומשם לספרד, כדי להשתתף במלחמת האזרחים. לאחר שחזרו, נשלחו אלכסנדר ואמו למחנות מעצר, ואילו אביו נשלח למחנה ריכוז, שם מת ב-$latex {1942}$.

מורה של גרותנדיק הכיר בכשרונו, ושלח אותו לפריס. שם כתב את הדוקטורט שלו באנליזה פונקציונלית, דוקטורט שכאמור הפך למשך שני עשורים לתנ"ך זוטא לאנשי התחום. אחר כך עבר לגיאומטריה אלגברית. שם במהרה הפך את התחום. צורת המחשבה שלו, השפה התאורית שבה נהג לקרוא לאובייקטים שעסק בהם, כמו זרעים, נבטים, וכו' הפכה לקלסית ומופיעה היום בכל ספר מודרני בגיאומטריה אלגברית. הגיאומטריה האלגברית חוקרת צורות הנתונות על-ידי פולינומים. צורות אלו נקראות יריעות. למשל, עיגול זה אוסף נקודות $latex {(x,y)}$ במישור כך ש-$latex {x^{2}+y^{2}=1}$. גרותנדיק אמר פעם שכשהוא גילה בילדות שצורה כל כך סימטרית ויפה נתונה על-ידי משוואה כל-כך פשוטה הוא הוקסם. אם נתונים $latex {N}$ פולינומים ב-$latex {m}$ משתנים

$latex \displaystyle f_{1}(x_{1},x_{2},…,x_{m}),\, f_{2}(x_{1},x_{2},…,x_{m})…,\, f_{N}(x_{1},x_{2},…,x_{m}) $

 וסף האפסים המשותפים שלהם נקרה יריעה אפינית. בגיאומטריה אלגברית לכל יריעה אפינית $latex {X}$מתאימים חוג הפונקציות הפולינומיאליות $latex {\mathcal{O}_{X}(X)}$ על היריעה. רעיון מרכזי של תחילת ואמצע מאה ה-$latex {20}$ היה שחוג הפונקציות אומר הכל על היריעה. כלומר בהינתן $latex {\mathcal{O}_{X}(X)}$ יש תהליך טבעי שמאפשר לשחזר בצורה חד משמעית את $latex {X}$.

גרותנדיק טען שמה שמעניין אינם אובייקטים מתמטיים, אלא הדרך שבה האובייקט מתייחס לאובייקטים אחרים בעולם. למשל, לא המספרים עצמם הם שמעניינים, אלא הפונקציות מן המספרים לאובייקטים אחרים. בעזרת המושגים המופשטים שהמציא הוא ולתלמידו פייר דלין הצליחו להוכיח השערה שנקראת "השערת רימן לשדות סופיים". זהו אחד המשפטים המרכזיים של המתמטיקה של המאה ה-$latex {20}$.

(השערת רימן היא כיום, לאחר שנפתרה השערת פרמה, ההשערה המפורסמת ביותר במתמטיקה, ומזה יותר ממאה שנים מכירים בה כהשערה המרכזית של תורת המספרים. שדה סופי הוא קבוצת מספרים סופית שעליה מוגדרות ארבע פעולות החשבון: חיבור, חיסור, כפל וחילוק בכל מספר שאינו אפס. דוגמה: המספרים מודולו מספר ראשוני. האם תוכלו למצוא מהו $latex {3:4}$ בשדה $latex {0,1,2,3,4}$ כשהכפל הוא מודולו $latex {5}$? כלומר - איזה מספר, כשכופלים אותו ב-$latex {5}$, משאיר שארית $latex {3}$ מ-$latex {5}$?)

בזכות הישגיו קיבל גרותנדיק ב-$latex {1966}$ את פרס פילדס, המקביל המתמטי של פרס נובל. הוא זכה בעוד פרסים יוקרתיים, אבל סירב לקבלם. כבן להורים מרדנים, ולעם נרדף, הפך לאנטי ממסדי יותר ויותר. בזמן מלחמת ויאטנם נסע לצפון ויאטנם ללמד את התושבים מתמטיקה. אחר כך סירב להמשיך במכון שהקימו בפריס, יש טוענים במיוחד עבורו, משום שטען שהוא ממומן על ידי כוחות אימפריאליסטים. הוא התחיל להתעניין בביולוגיה ובשימור הסביבה, וב-$latex {1988}$, בגיל $latex {60}$, פרש מחברת בני האדם ועבר להתגורר בהרי הפירנאים, בבקתה מבודדת. הוא המשיך לכתוב מתמטיקה, והותיר אחריו $latex {20,000}$ עמודי רשימות, שאותם ציווה להשמיד אחרי מותו. יש לשער שכמו במקרה של קפקא, שידידו מקס ברוד סירב למלא את צוואותו ולהשמיד את כל כתביו שלא פורסמו בעודו בחיים, גם במקרה זה הצוואה לא תקוים.

חידות

דניאל לובזנס

דבר העורך:  התכוננתי ל"מבול" של תשובות, אבל בעת כתיבת שורות אלו יש בקושי "זרזיף". נשמח לתגובותיכם גם אם לא תהיינה מלוות בפתרונות מלאים. בגיליון זה מפורסמים רק רמזים – הפתרונות המלאים יפורסמו בגיליון פברואר.

לחידות המוצגות בגיליון זה יפורסמו פתרונות בגיליון הבא. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 25.01.15,גם פתרונות לגיליון הקודם (לאחר שקבלתם רמזים) יתקבלו בברכה. אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.

חידה 1– שנת 2015 בפתח

יש להראות כי עבור כל $latex {N}$ טבעי, המספר :$latex {1000^N -1}$  איננו מחלק את המספר: $latex {2015^N -1}$.

חידה 2– מקלות הקטורת

ברשותכם $latex {2}$ מקלות קטורת, ידוע שכל מקל דולק בדיוק שעה אחת. המקלות אינם אחידים (כלומר קצב הבערה אינו קבוע) ברשותכם קופסה מלאה של גפרורים, כך שהנכם יכולים להדליק ולכבות את המקלות כרצונכם. איך ניתן לקבוע זמן של $latex {45}$ דקות בדיוק.

חידה 3– קידוח הנפט

$latex {4}$ אסדות תוחמות שטח קידוח נפט מלבני בים התיכון . מהאסדות הצפון-מערבית, צפון-מזרחית, ודרום-מזרחית נמדדו המרחקים לתחתית בור הקידוח: $latex {4,700}$ מ', $latex {5,200}$ מ', ו- $latex {3,200}$ מ' בהתאמה. מהו המרחק מהאסדה הדרום-מערבית לתחתית בור הקידוח?

רמזים לחידות מגיליון דצמבר 2014

חידה 1– היכן המטבעות המזויפות?  - יש לתת את הדעת שכששוקלים מספר מטבעות מזויפות המשקל קטן במספר זהה של גרמים.

חידה 2– הקוסם- נתן למצוא קשר בין השארית בחלוקה ל $latex {9}$ של המספר המחושב לשארית בחלוקה ל $latex {9}$ של המספר המקורי.

חידה 3 - ניסור קוביה – הסתכלו על הקובייה המרכזית שבתוך הקובייה של $latex {3*3*3}$.

חידה 4 - החשמלאי במגדל – ניתן לבצע את המטלה בעלייה אחת וירידה אחת עבור כל $latex {n>2}$. איך נתן לעשות זאת?