נטגר גליון 12
דבר העורך
רון אהרוני
לפני שאספר לכם מה יש בגיליון הנוכחי, בקשה: אנא כתבו לנו ב"תגובות" עד כמה חשוב לכם שהעיתון ימשיך להופיע. בהיעדר תגובות, המערכת מרגישה כמו קול קורא במדבר.
ועכשיו - לתוכן הגיליון הזה. אלכסנדר גיבנטל הוא מתמטיקאי ידוע מאוניברסיטת ברקלי, שמתעניין גם בהוראה לילדים. הוא כתב מאמר מאיר עיניים על שאלה שייתכן שבאיזשהו מקום היא מטרידה כל מתמטיקאי: מדוע משפט פיתגורס נכון. זהו משפט כה יסודי (ללא ספק המשפט החשוב ביותר בגיאומטריה), ועם זאת ההוכחות המקובלות אינן מסבירות את הסיבה העמוקה לנכונותו. הן נראות כמו להטוטי קסמים של העברת שטחים ממקום למקום. במאמר ניתנת ההוכחה ה"נכונה" (ואני אישית מסכים שהיא אכן ההוכחה האמיתית). תיהנו.
יש לנו ראיון עם מתמטיקאית ישראלית שאחראית, עם עוד שני מתמטיקאים, לפריצת דרך מרשימה בתורת המפרים: תמי ציגלר. לראיון הזה יש נופך מיוחד: המראיין הוא אביה, המתמטיקאי צבי ציגלר.
ויש לנו גם מאמר על המספר הקסום $latex {e}$ - ניסיון להסביר מדוע הוא כל כך מרכזי במתמטיקה.
וכמובן, מדור החידות של דני לובזנס.
בהנאה!
מספר קסום
אנה ליזהטוב
עניין מוזר: מבין כל המספרים הממשיים בחרה אלת המתמטיקה בשניים, ונתנה להם תפקיד מיוחד. אחד מהם, $latex \pi $, היה מוכר היטב עוד מימי קדם. זהו היחס בין היקף המעגל לקוטרו, שכבר הקדמונים ידעו שהוא שווה בכל המעגלים. הסימון "$latex \pi $" הופיע לראשונה בספר של וויליאם ג'ונס מ-1706, כאות הראשונה של "perimeter", כלומר היקף. המספר $latex \pi $ מופיע, כמובן, בנוסחאות גיאומטריות, אבל למרבה ההפתעה גם בהרבה הקשרים שאינם דווקא גיאומטריים, למשל בתורת המספרים - דוגמה אחת לכך נראה בהמשך הפרק. המספר השני, המסומן ב-$latex e $, התגלה רק במאה ה-17, משום שהבנת משמעותו דרשה כלים מן החשבון הדיפרנציאלי. חשיבותו התבררה רק לאיטה. הראשון שקרא לו בשם (אף כי לא בשם $latex e $, אלא $latex b $) היה המתמטיקאי והפילוסוף הגרמני לייבניץ (Gottfried Leibniz, 1646-1716). את השם $latex e $ נתן לו ליאונרד אוילר השוויצארי (Leonhard Euler, 1707-1783) , המתמטיקאי הגדול של המאה ה-18. מקור השם אינו באות הראשונה של שמו של אוילר, אלא בכך שאוילר רצה להשתמש באות שהיא תנועה, ומכיוון שהאות $latex a $ הייתה תפוסה אצלו לסימון דבר מה אחר בחר בתנועה השנייה על פי סדר האלף-בית.
תוך זמן קצר התברר שחשיבותו של $latex e $ אינה נופלת מזו של $latex \pi $. הוא מופיע באינספור הקשרים, ובהרבה תחומים. זהו "מספר עם עומק", ומשום כך "מספר יפה". כאן נציג אותו בשלושה הקשרים שבהם הוא מופיע.
ריבית דריבית
את המשמעות הראשונה של $latex e $ גילה המתמטיקאי השוויצארי יעקוב ברנולי (Jacob Bernoulli, 1654-1705) , והיא נוגעת לריבית דריבית, שפירושה ריבית שמתווספת לסכום המקורי, ואז מחושבת הריבית על הסכום הכולל. נניח שהִשקַעת 1000 ₪ בתוכנית חיסכון. אם אתה מרוויח כל שנה 10% על כספך, כמה כסף יהיה לך כעבור 10 שנים? התשובה הנאיבית היא שיהיו בידך 2000 ₪, משום שהרווח שלך יהיה 10 פעמים 10%, שהוא 100%. אבל האמת היא שיהיו בידך יותר. רווח של 10% כל שנה פירושו שכל שנה נכפל כספך פי $latex 1\frac{1}{10}$, או בסימון עשרוני –פי 1.1. אחרי שנה יהיו לך 1.1 כפול 1000, כלומר 1100 ₪. בסוף השנה השניה יהיו לך 1.1 כפול 1100, שהם 1121 ₪. בסוף השנה השלישית יהיו לך 1.1 כפול 1121, וכו'. אחרי $latex k$ שנים יהיו בידך $latex 100*1.1^k$₪. במיוחד, אחרי 10 שנים יהיו בידך $latex 100*1.1^{10}$ שקלים, ומכיוון ש-$latex 1.1^{10}$ הוא בערך 2.59, יהיו בידך כ-2590 ₪.
מה קורה אם אתה מרוויח כל שנה $latex \frac{1}{20}$ על כספך, ואתה מחכה 20 שנים? לפני שנשיב על כך, נעצור לרגע, ונשאל – האם התשובה תהיה יותר או פחות מן התשובה הקודמת, 2590? היא תהיה יותר. כדי לראות זאת, חלקו את 20 השנים ל-10 זוגות של שנים. לולא עניין ה"ריבית דריבית", שנתיים של ריבית של $latex \frac{1}{20}$ היו שקולות לשנה של ריבית של $latex \frac{1}{10}$. בגלל הריבית דריבית, הריבית על שנתיים עוקבות היא יותר מאשר $latex \frac{1}{10}$. לפיכך 10 זוגות השנים יניבו יותר מאשר 10 השנים בבעיה הקודמת. כלומר, ב-20 השנים תקבל יותר ריבית מאשר ב-10 שנים של ריבית של $latex \frac{1}{10}$. על פי חשבון דומה לקודם, אחרי 20 שנה יהיו בידך $latex 1000*(1+\frac{1}{20})^{20}$ שקלים.$latex (1+\frac{1}{20})^{20}$ הוא בערך 2.65, ולכן יהיו בידך כ-2650 שקלים (שהם, אכן יותר מ-2590). אם אתה מרוויח כל שנה $latex \frac{1}{50}$ על כספך, ואתה מחכה 50 שנים, יוכפל כספך פי $latex (1+\frac{1}{50})^{50}$ , שהוא בערך 2.69. אם אתה מרוויח אחוז אחד לשנה, אחרי 100 שנים יוכפל כספך $latex (1+\frac{1}{100})^{100}$, שהוא בערך 2.704.
סדרת המספרים שאנו מסתכלים בה היא של $latex (1+\frac{1}{n})^n$, ולפי הדוגמאות האלה רואים שהם הולכים וגדלים כאשר $latex n$ גדל. מצד שני, קצב הגדילה הולך ומואט. המספרים האלו אינם שואפים לאינסוף, אלא מתכנסים למספר שהוא גדול רק מעט מ-2.7. קירוב טוב יותר לגבול שלהם הוא 2.718. את הגבול שלהם מסמנים ב-$latex e$. זוהי אחת מכמה הגדרות שקולות למספר $latex e$,קרוב לוודאי שההגדרה המקובלת ביותר.
הממוצע הגיאומטרי של המספרים בין 1 ו-100
הדרך למצוא את סכום המספרים בין 1 ובין 100 היא על ידי חישוב הממוצע של המספרים האלה. הממוצע הוא האמצע בין 1 ו-100, כלומר $latex \frac{1+100}{2} = 50\frac{1}{2}$, וסכומם של כל המספרים בין 1 ובין 100 הוא 100 פעמים הממוצע הזה, כלומר $latex 100*50\frac{1}{2} = 5050$. הממוצע של המספרים הוא המספר שאם נחליף בו כל אחד מן המספרים, לא ישתנה הסכום. אם נחליף כל אחד מ-100 המספרים בין 1 ובין 100 ב-$latex 50\frac{1}{2}$, נקבל מספרים שסכומם הוא כסכום המספרים המקוריים – זוהי בעצם ההגדרה של הממוצע. אם, למשל, נחליף את המספרים 6 ו-8 בממוצעם, שהוא 7, נקבל במקום 6 ו-8 פעמיים את המספר 7, ואכן $latex 6+8=7+7=14$.
כאן עלי לספר לכם סוד, והוא שמה שבפי העם נקרא "ממוצע" נקרא בפי המתמטיקאים "ממוצע חשבוני". הצורך בשם מיוחד נובע מכך שיש עוד סוגי ממוצעים, שהמפורסם ביניהם הוא הממוצע הגיאומטרי. זהו המספר שאם נחליף בו את כל המספרים, לא תשתנה מכפלתם. למשל, הממוצע החשבוני בין 1 ו-100 הוא $latex 50\frac{1}{2}$, האמצע ביניהם. הממוצע הגיאומטרי, לעומת זאת, הוא 10, משום שאם תחליפו את 1 ואת 100 ב-10, תקבלו פעמיים את המספר 10, ואכן $latex 1*100 = 10*10$. הממוצע הגיאומטרי בין שני מספרים לא שליליים $latex a$ ו-$latex b$ הוא השורש של מכפלתם, כלומר $latex \sqrt{ab}$. הרי מכפלת $latex \sqrt{ab}$ בעצמו היא $latex \sqrt{ab}*\sqrt{ab}$, שעל פי הגדרת השורש שווה ל-$latex ab$ , כלומר מכפלת שני המספרים המקוריים. הממוצע הגיאומטרי של 100 מספרים הוא המספר שמכפלתו בעצמו 100 פעמים, כלומר חזקתו ה-100, שווה למכפלת המספרים המקוריים. כלומר, הוא השורש ה-100 של מכפלת המספרים.
מהו הממוצע הגיאומטרי של המספרים בין 1 ובין 100? כאמור, זהו השורש ה-100 של מכפלתם, כלומר השורש ה-100 של$latex 1*2*3*\dots*98*99*100$. את המספר $latex 1*2*3*\dots*98*99*100$ מסמנים ב-$latex 100!$, ובעל פה אומרים "100 עֲצֶרֶת" (באנגלית – 100 factorial). זהו מספר ענקי. אם נכתוב אותו בצורה עשרונית יהיו בו בערך 150 ספרות. האם גם אותו אפשר לחשב כפי שחישבנו את הסכום, בלי לחשב את כל 99 פעולות הכפל הנדרשות? מתברר שלא, אבל אפשר להעריך אותו בדיוק לא רע.
חישוב $latex 100!$ שקול לחישוב הממוצע הגיאומטרי של המספרים בין 1 ובין 100. הרי אם $latex x$ הוא הממוצע הגיאומטרי הזה, אז $latex 100! = x^{100}$, כלומר אם נדע את $latex x$ נדע את $latex 100!$. מצד שני, אם נדע את $latex 100!$ נדע את $latex x$, כי $latex x=\sqrt[100]{100!}$. האם ייתכן שהממוצע הגיאומטרי, $latex x$ , שווה לממוצע החשבוני, שהוא כזכור $latex 50\frac{1}{2}$? ההשערה הזאת רחוקה מאוד מן המציאות. לו כך היה, הייתה מכפלת המספרים בין 1 ו-100 שווה ל $latex 50\frac{1}{2}*50\frac{1}{2}*\dots$, מכפלת $latex 50\frac{1}{2}$ בעצמו 100 פעמים, כלומר $latex (50\frac{1}{2})^{100}$. אבל $latex (50\frac{1}{2})^{100}$ היא הערכה הרבה יותר מדי גבוהה ל-$latex 100!$. כדי לראות זאת שימו לב לכך ש: $latex 100*1<50\frac{1}{2}*50\frac{1}{2}$, וגם: $latex 90*2<50\frac{1}{2}*50\frac{1}{2}$, וכן גם: $latex 98*3<50\frac{1}{2}*50\frac{1}{2}$, וכו' – נקבל כך 50 אי-שוויונים. מדוע? משום שבאגף שמאל מופיעה בכל אחד מאי השוויונות מכפלה של מספרים שסכומם 101, ובאגף ימין מכפלה של מספרים שווים שסכומם 101. אגף שמאל הוא שטח של מלבן שסכום אורכו ורוחבו הוא 101, בעוד אגף ימין הוא שטח של ריבוע שסכום אורכו ורוחבו (שבריבוע הם שווים, כמובן) הוא 101. עובדה ידועה היא ששטח של ריבוע גדול משטח של מלבן בעל אותו היקף (נחזור לכך באחד הפרקים הבאים, שנושאו הוא סימטריה). מכפלת כל אגפי שמאל של 50 אי השוויונים האלו נותנת $latex 100!$, ואילו מכפלת אגפי ימין היא מכפלת $latex 50\frac{1}{2}$ בעצמו 100 פעמים, כלומר $latex (50\frac{1}{2})^{100}$ . מכיוון שבכל אי שוויון אגף ימין גדול יותר, גם מכפלת אגפי ימין גדולה יותר. מה שהראינו הוא למעשה ש: $latex x<50\frac{1}{2}$, כלומר הממוצע הגיאומטרי קטן מן הממוצע החשבוני. זוהי עובדה שנכונה תמיד, עם פחות או יותר אותה הוכחה, והיא נקראת "אי שוויון הממוצעים":
הממוצע הגיאומטרי של כל קבוצת מספרים קטן מן הממוצע החשבוני או שווה לו.
מצד שני, $latex 100!$ בוודאי גדול מ-,$latex 2^{100}$ משום ש-$latex 100!$ הוא מכפלת 100 מספרים שרובם גדולים בהרבה מ-2. המכפלה הזאת גדולה גם מ-$latex 10^{100}$, משום שרוב המספרים במכפלה גדולים בהרבה מ-10. מהו המספר הנכון, בין 1 ל-100, שמכפלתו בעצמו 100 פעמים תיתן $latex 100!$? במילים אחרות, מהו המספר $latex x$ ש- $latex x^{100} = 100!$? השתכנענו ש-$latex 10<x<50\frac{1}{2}$. אבל מהו? התשובה היא שזהו בערך $latex \frac{100}{e}$, שהוא בערך 36.79. כמובן, המספר 100 הוא רק דוגמה. חבויה כאן עובדה כללית, שאותה הראה ג'ימס סטרלינג (James Stirling, 1692-1770): הממוצע הגיאומטרי של המספרים בין 1 ל-$latex n$ הוא בערך $latex \frac{n}{e}$.
מה משמעותו של ה"בערך" הזה? הרי "בערך" אינו ניסוח מתמטי! ובכן, הדבר אומר שהיחס בין הממוצע הגיאומטרי האמור ובין $latex \frac{n}{e}$ הולך ומתקרב ל-1, כאשר $latex n$ הולך וגדל. כלומר שבגבול, היחס הזה הוא 1. הממוצע הגיאומטרי של המספרים בין 1 ו-$latex n$ הוא, בנוסחה:$latex \sqrt[n]{n!}$ . כלומר השורש ה- $latex n$ של $latex n!$, המספר שאם נעלה אותו בחזקת $latex n$ נקבל $latex n!$. ראינו זאת בדוגמה, כשהסברנו מדוע הממוצע הגיאומטרי של המספרים בין 1 ו-100 הוא $latex \sqrt[100]{100!}$. ובכן, סטרלינג הוכיח ש-$latex \frac{\sqrt[n]{n!}}{n/e}$ מתקרב והולך ל-1, ובסימון מתמטי:
$latex \lim\frac{\sqrt[n]{n!}}{n/e}=1$
למעשה, סטרלינג הוכיח הערכה מדויקת למדי ל-$latex n!$. הוא הראה שלערכי $latex n$ גדולים,
$latex n!\approx(\frac{n}{e})^n\sqrt{2\pi n}$
כאשר הסימון "$latex \approx$" משמעו, שוב, שאגף שמאל מחולק באגף ימין מתקרב והולך ל-1. למרבה הפלא, מופיע כאן גם המספר $latex \pi $, באורח לגמרי בלתי צפוי!
משוואה דיפרנציאלית
חיפושית עומדת במישור, בנקודה $latex (0,1) $, כלומר על ציר ה-$latex y$, בגובה 1 (ראה איור). היא מתחילה ללכת לכיוון ימין, לאורך קו ששיפועו הוא 1, כלומר בזווית של 45 מעלות (כמו באיור), שפירושו הוא שעל כל יחידה שהיא זזה בכיוון ימין היא עולה יחידה אחת. ככל שהחיפושית מתקדמת, היא משנה את הזווית של הליכתה – היא הולכת תמיד בשיפוע השווה בדיוק לגובהה. למשל, כשהיא מגיעה לגובה 2 מעל ציר ה-$latex x$, שיפוע הליכתה הוא 2, שפירושו שהיא עולה פי 2 מהר משהיא זזה ימינה.
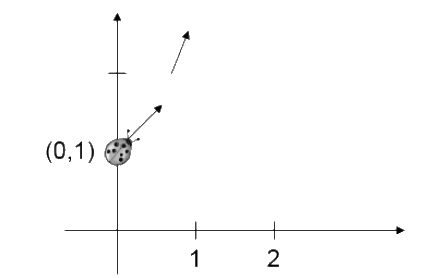
החיפושית הולכת ימינה ולמעלה. היחס בין התקדמותה כלפי מעלה ותזוזתה ימינה הולך וגדל:הוא שווה לגובה של החיפושית על ציר ה-$latex x$.אפשר אז להוכיח שכאשר החיפושית מתקדמת $latex x$ יחידות ימינה, היא נמצאת בגובה $latex e^2$.
כמובן, החיפושית תנסוק מהר מאוד. הרי ככל שהיא מגביהה, גם קצב עלייתה גדל. השאלה היא: מהי הנוסחה של העקום שהיא הולכת לאורכו? כלומר, לאחר שהלכה $latex x$ יחידות ימינה, באיזה גובה תהיה? התשובה היא שנוסחת העקום היא $latex y=e^x$. כלומר, לאחר שהחיפושית תנוע $latex x$ יחידות ימינה, היא תהיה בגובה $latex e^x$. למשל, אחרי יחידת זמן אחת, היא תהיה בגובה $latex e$. אחרי שתי יחידות זמן, היא תהיה בגובה $latex e^2$. במונחים הלקוחים מן החשבון הדיפרנציאלי, לפונקציה $latex e^x$ יש תכונה ייחודית, שהיא שווה לנגזרת שלה (הנגזרת של פונקציה היא קצב השינוי שלה). זהו ייחודו של המספר $latex e$, ולמעשה זהו הייחוד שממנו נובעות כל שאר תכונותיו. הפונקציה $latex e^x$, אגב, אכן נוסקת מהר מאוד: למשל, אחרי 10 יחידות תזוּזה ימינה, החיפושית תהיה כבר בערך בגובה 6000 יחידות.
מה שתיארנו כאן נקרא "משוואה דיפרנציאלית". משוואה דיפרנציאלית מתארת את התנהגותו של עקום. היא מספרת מהו שיפועו של העקום, כלומר קצב עלייתו של ערך $latex y$ כשהולכים לאורך העקום, בכל נקודה על העקום. במשוואות דיפרנציאליות מסובכות יותר יכול להינתן קשר בין הנקודה שבה נמצאים על העקום, לבין שיפועו של העקום, ובין קצב השינוי מסדר שני, כלומר באיזה קצב משתנה קצב העלייה או הירידה של העקום. משוואות דיפרנציאליות מתארות אפוא את הגיאומטריה של עקומים, במונחים של קצב השינוי שלהם. לצערי, בתור סטודנט לא הבנתי את משמעותן הגיאומטרית של משוואות דיפרנציאליות, ולא תפסתי את יופין. למעשה, תחום המשוואות הדיפרנציאליות הוא גם יפה וגם שימושי. המספר $latex e$ מופיע בו תדירות.
ההוכחה הנכונה למשפט פיתגורס
אלכסנדר גיבנטל
על אף שמשפט פיתגורס הוא כבר בן למעלה מאלפיים וחמש מאות שנים, הוא עדיין בעל חיוניות ועניין גם לבני דורנו. הוא המפתח לנוסחת המרחק בין נקודות במישור, שפירושו שהוא נמצא בכל מודל במדע ובהנדסה שמכיל גיאומטריה או טריגונומטריה. הוא שותף סמוי למכפלה הסקלרית של וקטורים, ובתפקיד הזה הוא ממלא מקום במשוואות היסודיות של הפיזיקה. הוא הרוח החיה מאחורי משוואות תורת היחסות הפרטית ותורת הקוואנטים. הוא גם אחד המשפטים היחידים שמוכרים בציבור הרחב עם הוכחה.
מאות הוכחות יש למשפט. רובן בעלות אותו אופי: גזירה והרכבה מחדש של צורות. למשל, כמו בהוכחה המשכנעת הבאה:
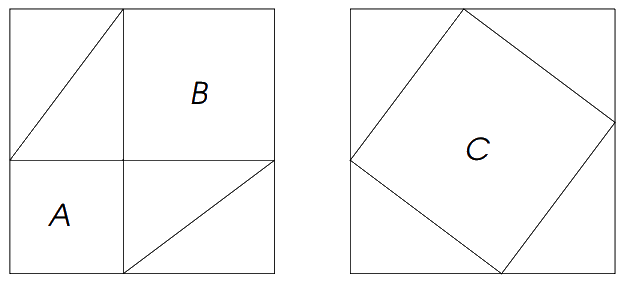
אבל ההוכחות האלה משאירות אותנו בתהייה: אחת העובדות הבסיסיות ביותר בטבע היא בסך הכל עניין של גזירה וצירוף מחדש.
לאחרונה עלעלתי בכתביו של אוקלידס, והגעתי להוכחה שמרבית חברי אומרים עליה שהיא הראשונה שהם מבינים באמת. היא לא רק קצרה ופשוטה, אלא גם אינה נעשית על דרך של קסם של גזירה. היא מגיעה ללב העניין.
משפט פיתגורס, שידוע גם כ"אוקלידס $latex {I.47}$" אומר שסכום שטחי הריבועים שבנויים על הניצבים של משולש ישר זווית שווה לשטח הריבוע הבנוי על היתר. מתברר שבספר השישי של אוקלידס יש הכללה הרבה פחות מפורסמת, שתופסת את המשפט בקרניו. אין זו חובה שעל צלעות המשולש ייבנו ריבועים. מספיק שהצורות יהיו דומות. למשל, חצאי עיגולים, כמו בציור הבא:
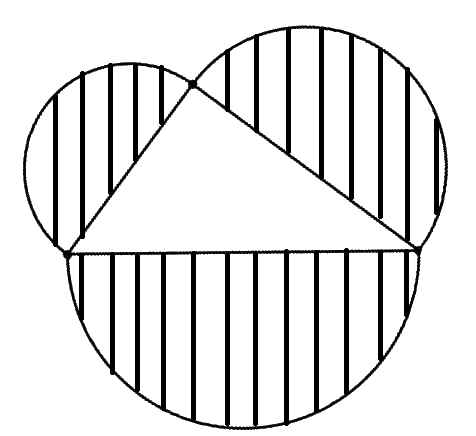
הרי השטח פרופורציוני לריבוע של הצלע. מצד שני - מספיק להוכיח שוויון לעיגולים: פירוש שוויון השטחים הוא (חישבו מדוע) ש: $latex {\pi \frac{a^2}{8}+\pi \frac{b^2}{8}=\pi \frac{c^2}{8}}$, שנותן מייד את המשפט.
למעשה מספיק להראות לצורה אחת ושתי צורות דומות לה, שסכום שטח שתי הצורות על הניצבים שווה לשטח הצורה הבנויה על היתר. הפרופורציונליות לריבוע הצלע תעשה את העבודה.
אבל אם כך, מדוע לא לשים על הצלעות משולשים, כמו בציור הבא?

הסתכלו באיור. נאמר שאורכי הניצבים של המשולש הם $latex {a}$ - $latex {b}$, ואורך היתר הוא $latex {c}$.
נאמר ששטח המשולש הבנוי על היתר הוא $latex {s}$. אזי השטח של המשולשים על הניצבים הם $latex {\frac{a^2}{c^2}s}$ ו-$latex {\frac{b^2}{c^2}s}$ בהתאמה. (שטח של משולשים דומים נמצא ביחס ישר לריבוע האורכים שלהם: אם מגדילים את האורכים במשולש פי $latex {\alpha}$ אז גם האורך וגם הרוחב של המשולש גדלים פי $latex {\alpha}$, ולכן שטח המשולש גדל פי $latex {\alpha^2}$).
המשולשים שעל הניצבים חופפים לשני המשולשים שמחלקים את המשולש המקורי, ואילו המשולש שעל היתר חופף למשולש המקורי. לכן סכום שטחי המשולשים על הניצבים שווה לשטח המשולש על היתר, כלומר
$latex \displaystyle \frac{a^2}{c^2}s + \frac{b^2}{c^2}s =s$
וצמצום ב-$latex {s}$ נותן
$latex \displaystyle \frac{a^2}{c^2} + \frac{b^2}{c^2} =1$
שהוא משפט פיתגורס.
ראיון עם פרופסור תמר ציגלר
צבי ציגלר
המראיין הוא פרופ' אמריטוס צבי ציגלר, מהפקולטה למתמטיקה בטכניון. המרואיינת היא פרופ' תמר ציגלר, מהחוג למתמטיקה באוניברסיטה העברית.
צ: הרעיון לראיין אותך הוא של עורכי העיתון. נחמד יהיה ללמוד דברים חדשים על הבת שלי. שאלה ראשונה- האם חשבת שמתמטיקה מעניינת אותך כבר כשהיית ילדה?
ת : לא. כשהייתי ילדה חשבתי שמעניינות אותי חידות קשות, אבל לא התעניינתי במיוחד במתמטיקה.
צ: וכשגדלת והיית בתיכון ?
ת: גם אז לא. אהבתי כל מיני דברים, כמו לנגן ולטייל ולא חשבתי בכלל על מה ארצה לעשות כשאהיה גדולה.
צ: אז מתי תקף אותך החיידק המתמטי?
ת:החלטתי שאני אוהבת מתמטיקה בתקופת הצבא והיה ברור לי שבסיום השירות הצבאי שלי אלך ללמוד מתמטיקה, בלי לחשוב אם זה יהיה התחום בו אעסוק לאחר מכן. מאד אהבתי את תקופת הלימודים באוניברסיטה העברית, ונהניתי מהקורסים.
צ: מכל הקורסים ? בשנה הראשונה לומדים מתמטיקה ופיסיקה – האם גם הפיסיקה משכה אותך? האם היה קורס הזכור לך במיוחד, או שהשפיע עלייך במיוחד?
ת: אהבתי את הקורסים במתמטיקה הרבה יותר מאשר אלו של פיסיקה, כי בפיסיקה היו הרבה הנחות ואי בהירות, ומתמטיקה היא מדויקת במידה חסרת-פשרות. הדיוק והניקיון במערכת של הנחות והוכחות המבוססות על ההנחות ועל היקשים לוגיים, קסמו לי במיוחד. מהקורסים זכור לי לטובה במיוחד הקורס של פרופ' אומן, בעיקר תודות לבדיחות.
צ. השתמשת בביטוי "קסמו לי". האם את מוצאת קסם או יופי מיוחד במתמטיקה ?
ת : מתמטיקה טובה היא יפהפיה – כמו תמונה יפה שאי אפשר להפסיק להתפעל ממנה.
צ: היה לך קשר מיוחד עם סטודנטים אחרים באותה תקופה? למדת ביחד עם אחרים?
ת: כן….את בעלי הכרתי בלימודים….אבל בעיקר אהבתי ללמוד לבד ולהתמודד עם בעיות לבד.
צ: וכשסיימת ללמוד ידעת שתרצי לעסוק במתמטיקה כקריירה?
ת: ידעתי שאני רוצה להמשיך לתואר שני. וכשסיימתי תואר שני, ידעתי שאני רוצה להמשיך ולחקור ונרשמתי ללימודי דוקטורט, אבל גם בשלב זה לא היה ברור לי שאני מעוניינת בקריירה של מתמטיקאית. בלימודי התואר השלישי, אחרי שנולד הבן השני שלי, הייתה תקופה שנתקעתי, היו לי ספקות באשר ליכולת שלי, אבל בסופו של דבר הייתה לי פריצת דרך. בכל שלב הסתכלתי רק צעד אחד קדימה – בשלב זה כבר חשבתי שיכול להיות שאהיה מתמטיקאית של ממש, אבל הסתכלתי רק על הפוסט-דוקטורט.
צ: האם את יכולה לומר משהו, במילים לא יותר מדי מקצועיות, על התוצאות העיקריות בעבודת הדוקטורט שלך ? התוצאות והרעיונות מעבודה זו ממשיכים להשפיע על עבודתך גם זמן רב לאחר סיום העבודה, נכון?
ת: עבודת הדוקטורט שלי עסקה בנושא של חזרה מרובה במערכות דינמיות. בתקופה ההיא זה היה נושא די אזוטרי במתמטיקה אבל לי הוא קסם מאד. בתקופת הפוסט דוקטורט שלי הנושא הפך מאד מרכזי בעקבות העבודה של גרין וטאו על קיום סדרות חשבוניות מכל אורך סופי במספרים הראשוניים. העבודה שלהם הייתה מבוססת על רעיונות שהיו קשורים לנושא שחקרתי בדוקטורט. בעקבות העבודה שלהם התחלתי להתעניין בשאלות לגבי מבנים מעניינים בראשוניים, והרעיונות מעבודת הדוקטורט הובילו לתרומותיי לתחום.
צ: הפוסט דוקטורט שלך כלל שנה במכון ללימודים מתקדמים בפרינסטון. תארי את האווירה שם ואיך היא השפיעה על עבודתך.
ת: המכון, כמקום לבלות בו שנה, הוא מקום פנטסטי. אוירה קסומה, שקט נפשי, אפשרות להתנתק מהכל ורק לחשוב. אני חושבת שזו הייתה השנה המשמעותית ביותר להתפתחות שלי כמתמטיקאית. רק שם הגעתי למסקנה שאני באמת בוחרת במקצוע הזה כקריירה ואני ראויה להיקרא מתמטיקאית. יתר על כן, רק בתקופה ההיא התחלתי לדבר עם מתמטיקאים אחרים על מתמטיקה ולעבוד ביחד על בעיות.
צ: עד אז לא היו לך הזדמנויות לשתף פעולה, או שנרתעת מזה.
ת: לא כל כך ברור מה הסיבה, אולי כי הרגשתי לא נוח לדבר על דברים שלא הבנתי עד הסוף. העובדה היא שאפילו בשנות הפוסט-דוקטורט הראשונות שלי נהגתי לעבוד לבד, ורק ההיכרות שלי עם פרופ' טרי טאו מאוניברסיטת קליפורניה, שהזמין אותי לביקור מקצועי באוניברסיטה שלו, שינתה את ההתייחסות שלי לשיתופי פעולה. פתאום מצאתי את עצמי מדברת אתו ועם מתמטיקאים אחרים, מחליפה רעיונות וכיווני מחשבה.
צ. ההישגים הגדולים שלך החלו בתקופה זו, בה תרמת לפתרון בעיות שהטרידו דורות של מתמטיקאים ולא זכו לפתרון. ההתחלה הייתה אז, אבל ההבשלה באה שנים מספר אחר מכן. האם תוכלי לתאר את הבעיה ואת הרעיונות שסייעו לך בפתרונה?
ת: הבעיה ששבתה אותי הייתה מציאת פתרון של מערכות משוואות לינאריות במשתנים שהם מספרים ראשוניים והערכת מספר הפתרונות. אחת הבעיות בחקר המספרים הראשוניים היא שיש מעט מספרים ראשוניים – מבין המספרים בין 1 ל –N יש רק בערך N/logN מספרים ראשוניים. בעיית הדוקטורט שלי עסקה בשאלות הקשורות לפתרון משוואות כאלה בתוך תתי קבוצות עם צפיפות חיובית במספרים הטבעיים – למשל בתתי קבוצות המהוות אחוז אחד מהמספרים הטבעיים – דרך הבנת תופעת החזרה המרובה בדינמיקה. שילוב של רעיונות מדינמיקה והתקדמויות בהבנת מבנה המספרים הראשוניים הוביל בסופו של דבר לפתרון הבעייה עבור מערכות משוואות לינאריות רבות.
צ. התחרותיות במתמטיקה היא עצומה. כולם רוצים לפתור את הבעיות הקשות ולהשאיר חותם לדורות הבאים. האם לדעתך המתמטיקאים מפרגנים למי שמצליח לפתור בעיות ולהגיע להישגים, או שהקנאה גוברת ?
ת: אמנם נתקלתי בראשית הקריירה גם במקרים של צרות עין, אבל ככלל המתמטיקאים מתלהבים מהישגים של אחרים וכשמישהו פותר בעיות שהיו ללא פתרון או מגיע להישגים מדהימים – התגובה היא התפעלות כללית, וברכות מכל עבר. הדוגמא של צ'אנג בנושא המספרים התאומים היא טיפוסית.
צ: את יכולה לפרט ?
ת: צ'אנג הוא מתמטיקאי מבוגר מאוניברסיטה קטנה ושולית בארה"ב, שעיקר עיסוקה בהוראה. הסתבר שהוא עבד במשך שנים על בעיה מאד מפורסמת בתורת המספרים – בעיית המספרים הראשוניים התאומים (זוגות מספרים ראשוניים שההפרש ביניהם 2).הוא הצליח במקום שבו כל המומחים נכשלו והראה שיש אינסוף זוגות מספרים ראשוניים שההפרש ביניהם קטן מ- 70,000,000. זו הייתה פריצת דרך ענקית והוא זכה מייד בפרגון והערכה רבה מכל הקהילה המתמטית.
צ: בסופו של יום – כיף להיות מתמטיקאית ?
ת: לי כיף. אני עושה מה שאני ממש אוהבת, וחופשיה לעשות זאת בדרך המוצאת חן בעיניי.
חידות
דניאל לובזנס
דבר העורך: לצערי עדיין מעטים מכם שולחים פתרונות. עד עכשיו הגיע רק פתרון נכון אחד, לחידה $latex 2$ בגיליון ינואר, וגם פותרה מעדיף ששמו לא יפורסם. על מנת שהחידות תהינה בתחום המעניין אתכם (לא קשות מדי, כדי שתצליחו לפתור, אבל מספיק מאתגרות כדי שתהינו מפתרונן), אודה גם לתגובות (ולאו דווקא פתרונות) בטופס שבתחתית העמוד.
לחידות המוצגות בגיליון זה יפורסמו פתרונות בגיליון הבא. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 23.2.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1– סכומים של ספרות?
קל לחשב את סכומם של מספרים עוקבים (למשל מ $latex 1$ עד $latex 10$ הסכום הוא $latex 55$), קשה יותר לחשב את סכום הספרות שלהם (סכום הספרות של המספרים מ $latex 1$ עד $latex 10$ הוא $latex 46$ ). התוכלו לחשב את סכום הספרות של המספרים מ $latex 1$ עד $latex 1,000,000$ ?
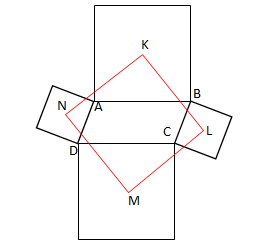
חידה 2– מרכזי ריבועים על גבי מקבילית?
נתונה מקבילית $latex ABCD$ על כל אחת מצלעותיה בונים ריבוע כלפי חוץ, כמתואר בשרטוט. יש להוכיח כי מרכזי הריבועים $latex K,L,M,N$ נמצאים על קדקודיו של ריבוע.
חידה 3– סכום של הופכיים?
נתונים $latex n$ מספרים טבעיים, שונים זה מזה $latex a_1,a_2,a_3,\dots,a_n$, כאשר ידוע שלאף אחד מהמספרים $latex a_i$ אין אף גורם ראשוני גדול או שווה ל $latex 5$.
יש להוכיח כי סכום ההופכיים שלהם קטן מ $latex 3$.
$latex s=\sum\limits_{i=1}^{i=n} \frac{1}{a_i}=\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\dots+\frac{1}{a_n}<3$
רמזים לחידות מגיליון ינואר 2015
חידה 1– שנת 2015 בפתח - בדקו האם המספרים מתחלקים, ללא שארית, ב-$latex 13$ וב- $latex 9$ .
חידה 2– מקלות הקטורת - לכל מקל יש שני קצוות. יש לתת את הדעת שאי אפשר לסמוך על זמני הבעירה של הגפרורים, הם אינם קבועים.
חידה 3– קידוח הנפט – הראו כי בכל מלבן ניתן לחשב את המרחק מנקודה כלשהיא במישור לאחד מקדקודיו אם ידועים המרחקים לשאר הקדקודים (זאת בלי תלות בממדי המלבן) – הכלילו התוצאה לנקודה כלשהיא במרחב.
פתרון החידות גיליון דצמבר 2014
חידה 1– היכן המטבעות המזויפים?
לוקחים מטבע $latex 1$ מערמה מס' $latex 2,1$ מטבעות מערמה מס' $latex 9,\dots,2$ מטבעות מערמה מס' $latex 9$. אילו כל המטבעות היו אמתיים משקלם הכולל היה $latex 45*7 = 315$ גרם. אם בערמה מס' $latex n$ יש מטבעות מזויפים המשקל הכולל יפחת ב-$latex n$ גרם. כלומר מספיקה שקילה אחת לגילוי ערמת המטבעות המזויפים.
כאשר יש רק $latex 3$ מטבעות בכל ערמה, מחלקים את הערמות ל $latex 3$ קבוצות בכך אחת $latex 3$ ערמות :
קבוצה $latex 1$ – ערמות $latex 1,2,3$
קבוצה $latex 2$ – ערמות $latex 4,5,6$
קבוצה $latex 3$ – ערמות $latex 7,8,9$
שוקלים מטבע אחד מכל אחת מהערמות שבקבוצה $latex 2,1$ מטבעות מכל אחת מהערמות בקבוצה $latex 2$, ו $latex 3$ מטבעות מקבוצה $latex 3$. סה"כ $latex 1*3+2*3+3*3=18$ מטבעות, אילו כולם היו אמתיים משקלם יהיה $latex 126$ גרם. המשקל הכולל יפחת ב- $latex n$ גרם אם ערימת המטבעות המזויפים שייכת לקבוצה $latex n$. עכשיו מתוך $latex 3$ ערמות המטבעות בקבוצה $latex n$ לוקחים מטבע אחד מהערמה הראשונה $latex 2$ מטבעות מהשנייה ו $latex 3$ מטבעות מהשלישית, סה"כ $latex 6$ מטבעות שמשקלם, אילו כולם אמתיים יהיה $latex 42$ גרם. המשקל הכולל יפחת ב $latex 1,2$ , או $latex 3$ גרם בהתאם למספר המטבעות שנלקחו מכל אחת מהערמות. כלומר שבמקרה זה נדרשות שתי שקילות לגילוי ערמת המטבעות המזויפים.
חידה 2– הקוסם
נסמן ב $latex X$ את המספר שחשבנו עליו וב $latex A$ את הערך המחושב שנמסר ל"קוסם" . כמו כן נסמן ב-$latex S_x$ את סכום הספרות של $latex X$ , ואת השארית בחלוקה ב $latex 9$ של מספר כל שהוא $latex y$ ב $latex R(y)$ (בסימונים המקובלים: $latex R(y)= R MOD 9$).
קל לראות כי אם נסכם את כל $latex 6$ המספרים המתקבלים מתמורות של ספרות $latex X$ התוצאה תהיה $latex 222*S_x$ מאחר ולחישוב $latex A$ לא מסכמים את $latex X$ הרי ש: $latex (*)A=222*S_x-X$ , ברור שידיעת $latex S_x$ תיתן לנו תשובה לבעיה.
קל לראות מ$latex (*)$ כי $latex \frac{A}{222}<S_x\le\frac{A}{222}+\frac{X}{222}$ ומאחר ו- $latex \frac{A}{222}<S_x<\frac{A}{222}+5, X<1000$, כלומר הערך של $latex S_x$ מוגבל ל-$latex 6$ אפשרויות בלבד, ואם נדע מה השארית שלו בחלוקה ל $latex 9$ נוכל לקבוע את ערכו.
נכתוב את משוואה $latex (*)$ בערכי שאריות מ$latex 9$ ונקבל
$latex R(A)=R(222)*R(S_x)-R(X) = 6*R(S_x)-R(S_x)=5*R(S_x)$
ולכן : $latex R(S_x)=R(2*R(A))$
כלומר ה"קוסם" לוקח את המספר $latex A$ מוצא את השארית בחלקה ב$latex 9$ (זה פשוט, ע"י סיכום הספרות) מכפיל ב $latex 2$ ומוצא את השארית של $latex S_x$ בחלוקה ב $latex 9$ .
אח"כ מחלק את $latex A$ ב $latex 222$ ומעגל כלפי מעלה למספר שהשארית שלו בחלוקה ב$latex 9$ זהה למה שחשב קודם, וזה יהיה $latex S_x$. ומכאן:$latex X=222*S_x-A$. מאחר והשיטה שלנו מחשבת באופן חד ערכי את $latex X$ מ$latex A$ ברור כי מהרמז ניתן לחשב את המספר המקורי והתשובה היא יחידה.
דוגמא:
נאמר כי הרמז הוא $latex A=3095$.
מאחר והשארית של $latex A$ בחלוקה ל $latex 9$ היא $latex 8$, השארית בחלוקה ל $latex 9$ של היא 7 . ($latex 8*2 MOD 9=16 MOD 9=7$)
הכפולה הקטנה ביותר של $latex 222$ הגדולה מ $latex A$ היא $latex 14$ (שארית $latex 5$ בחלוקה ב $latex 9$) ולכן המספר הקטן ביותר הגדול ממנה ששאריתו בחלוקה ל $latex 9$ היא $latex 7$ יהיה $latex 16$
ולכן: $latex X=222*16-3095=457$
כל מה שה"קוסם" צריך לדעת זה להכפיל ולחלק ב – $latex 222$ (ולכן רצוי שישנן את לוח הכפל של $latex 222$ מ $latex 222*1$ עד$latex 222*27$) וכמובן לחבר ולחסר מספרים בני $latex 4$ ספרות. אני בטוח שכל אחד מכם יוכל לאחר אמון קצר להציג "קסם" זה.
חידה 3 - ניסור קובייה
תנו דעתכם על הקובייה הקטנה המרכזית. יש לה $latex 6$ דפנות שכל אחת מהן צריך להפריד בניסור אחד משכנתה, סה"כ $latex 6$ צעדי ניסור. ולכן $latex 6$ הוא מספר צעדי הניסור המינימלי במקרה זה.
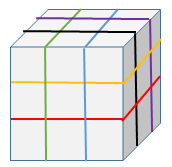
לגבי קובייה של $latex 4*4*4$ אפשר לחלק אותה ל $latex 2$ בכל אחד מהמישורים הראשיים ע"י $latex 3$ צעדי ניסור ולקבל $latex 8$ קוביות של $latex 2*2*2$. ניתן להציב $latex 8$ קוביות אלו זו על גבי זו וב $latex 2$ צעדי ניסור להפריד כל אחת ל $latex 4$ תיבת של $latex 2*1*1$, סה"כ $latex 32$ תיבות. נציב אותן זו על גבי זו ובניסור נוסף נחלק כל אחת ל$latex 2$ קוביות קטנות. סה"כ $latex 6$ צעדי ניסור, כמובן שאי אפשר בפחות כי גם כאן יש קוביות פנימיות כמו במקרה הקודם.
חידה 4 - החשמלאי במגדל
נראה שניתן לפתור את הבעיה בעליה אחת וירידה אחת.
נתחיל במקרה בו מספר החוטים אי זוגי $latex n=2m+1$. החשמלאי יסמן את קצות החוטים בסימון $latex b_1,b_2,b_3,\dots,b_n$
הקצה $latex b_1$ לא יחובר ואילו שאר הקצוות יחוברו בזוגות: כל קצה חוט $latex b_{2i}$ יחובר לקצה חוט $latex b_{2i+1}$.
החשמלאי יעלה לקומת הגג של המגדל, שם בעזרת בדיקת רציפות חשמלית בין כל הזוגות ימצא את החוט הבודד שאינו מחובר לאף אחד אחר ויסמנו במספר $latex 1$. אח"כ יסמן קצה חוט כל שהוא במספר $latex 2$ ואת החוט המחובר אליו חשמלית ב-$latex 3$ וימשיך יסמן את שאר החוטים במספרים $latex 4$ עד $latex n$ כאשר תמיד המספר $latex 2i+1$ יינתן לקצה המחובר חשמלית לקצה חוט מספר $latex 2i$. החשמלאי יחבר חשמלית בקומת הגג את זוגות החוטים
$latex 2i$ ו $latex 2i-1$.
(כלומר קצה $latex 1$ לקצה $latex 3,2$ ל-$latex 4$ וכן הלאה)
באיור המצורף מובא המקרה של $latex 7$ חוטים, הקווים האדומים מראים את החיבורים החשמליים בקומת הקרקע והירוקים בקומת הגג.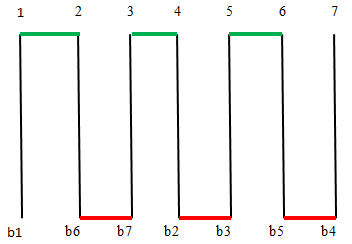
החשמלאי יורד לקומת הקרקע, ושם מסמן את קצה החוט $latex b_1$ במספר $latex 1$. מפרק את כל החיבורים החשמליים (אחרת כל החוטים יהיו מחוברים זה אל זה). החשמלאי מוצא מי מחובר לקצה $latex 1$ ומסמן אותו במספר $latex 2$ ואילו את בן זוגו (בן זוגו של הקצה שסומן ב$latex b_j$ הוא $latex b_{j+1}$ אם $latex j$ זוגי, ו-$latex b_{j-1}$ אם $latex j$ אי-זוגי) במספר $latex 3$. וממשיך באותה דרך, הקצה שמחובר חשמלית למספר $latex 3$ הוא מספר $latex 4$ ובן זוגו הוא מספר $latex 5$, וכן הלאה.
במקרה שמספר חוטים זוגי: $latex n=2m+2$, החשמלאי בקומת הקרקע מסמן את החוטים כמו קודם ומחבר חשמלית את הקצוות כמו במקרה האי זוגי כך שהקצוות $latex b_1$ ו$latex b_n$ אינם מחוברים. החשמלאי עולה לקומת הגג ומאתר את $latex 2$ קצות החוט שאינם מחוברים חשמלית לאף קצה אחר, אחד מהם הוא מסמן במספר $latex 1$ ואת השני במספר $latex n$. החשמלאי ממשיך בסימונים ובחיבורים כמו במקרה האי-זוגי. החשמלאי יורד לקומת הקרקע שם הוא בודק את הקצוות $latex b_1$ ו$latex b_n$ ומוצא מי מהם אינו מחובר לשאר הקצוות אותו הוא מסמן ב $latex n$ , ואת האחר במספר $latex 1$,וממשיך בבדיקות ובסימונים כמו במקרה האי-זוגי.
חידה יפה זו פורסמה ע"י (Martin Gardner (1914-2010 שהיה ממחברי החידות המתמטיות היותר פוריים ויצירתיים, במדור החידות שלו בירחון Scientific American לפני יותר מ $latex 50$ שנים – ישנן עוד שיטות לפתרון הדורש עליה וירידה אחת מהחשמלאי, אבל פתרון זה הוא האלגנטי ביותר.