נטגר גליון 14
דבר העורך
רון אהרוני
בגיליון הקודם סיפרנו על עקרון שובך היונים: אם יש יותר יונים מתאים, אז לפחות שתי יונים יצטרכו להצטופף באותו תא. תמונת מראה של העיקרון הזה היא שאם יש פחות יונים מתאים, יישאר תא ריק. המתמטיקאי דן עמיר טבע לעיקרון הזה את השם "עקרון הכיסאות המוזיקליים" (מי שמכיר את המשחק הזה מבין מדוע, אף על פי ששם בני אדם הם שנשארים "ריקים" - ריקים מכסאות). גם הוא, כמו עקרון שובך היונים, פשוט מאוד - החוכמה אינה בעצם השימוש בו אלא בבחירה של התאים ושל היונים. במאמר של אנה ליזהטוב יסופר על שימוש גיאומטרי לעיקרון הזה. גם כאן יש נקודה ישראלית - בעל הטיעון הוא מיכה פרלס מן האוניברסיטה העברית.
יש גם השערה, שהיא הכללה של המשפט שעל הוכחתו מסופר במאמר. זוהי השערה של המתמטיקאי האנגלי-אמריקאי המפורסם ג'ון קונווי. השערה שנראית כאילו כל ילד יכול לפתור אותה. נסו!
ויש גם הוכחה יפה למשפט ישן, של קיילי, על ספירת עצים. בעל ההוכחה הוא דניאל קלייטמן, מ-$latex {MIT}$. את המאמר כתב עבורנו כתבנו הוותיק אליהו לוי.
חידוש נוסף לאתר! העלנו לרווחתכם את "רבעון למתמטיקה" - בין הגליונות המתמטיים הותיקים אם לא הותיק ביותר. איכות הקבצים היא סריקה אך זהו אוצר שלא יסולא בפז, תהנו.
עקרון הכיסאות המוזיקליים
אנה ליזהטוב
בגיליון הקודם סיפרנו על עקרון שובך היונים: אם יש יותר יונים מתאים, שתיים מהן תצטרכנה להצטופף באותו תא. עיקרון פשוט עוד יותר הוא בכיוון ההפוך: אם יש פחות יונים מאשר תאים, לפחות תא אחד יישאר ריק. כפי שאם יש פחות כיסאות מאנשים במשחק הכיסאות המוזיקליים יהיה אדם ללא כיסא (את השם "עקרון הכיסאות המוזיקליים" הציע המתמטיקאי דן עמיר). או, שאם קונים $latex 99$ שלגונים ל-ִ$latex 100$ ילדים, יהיה ילד שלא יקבל שלגון. פשוט? ובכן, כמו במקרה של עקרון שובך היונים, תלוי איך משתמשים בזה. הנה משפט שנראה פשוט, אבל איני מכיר לו שום הוכחה פשוטה.
משפט: בהינתן נקודות במישור וקטעים המחברים ביניהן, אם יש יותר קטעים מנקודות אזי בין הקטעים הנתונים יש שניים שאינם נפגשים.
אם מספרם של הקטעים שווה למספר הנקודות, ייתכן מאוד שכל שני קטעים ייפגשו. בכל אחת משתי הדוגמאות שלהלן, למשל, יש $latex 5$ נקודות ו-$latex 5$ קטעים, וכל שני קטעים נפגשים, אם בקצותיהם ואם בנקודות שבתוכם:
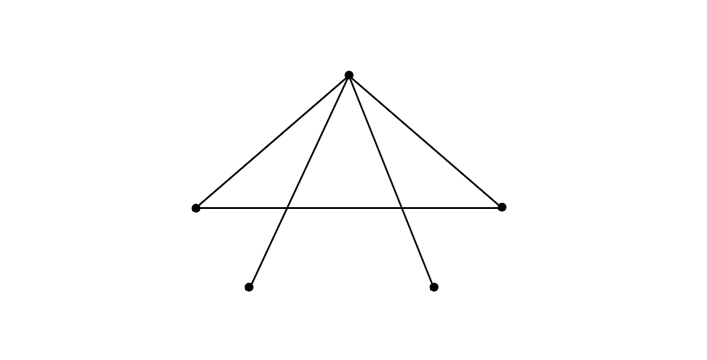
אבל אם $latex 5$ קטעים יעברו בין $latex 4$ נקודות (כך שיש יותר קטעים מנקודות) שניים מביניהם יהיו "זרים" (לא נפגשים). למשל:
כאן יש יותר קטעים מנקודות – $latex 5$ קטעים כנגד $latex 4$ נקודות. המשפט אומר שבמקרה כזה יש שני קטעים שאינם נפגשים. ואומנם כך הוא – הקטע $latex AD$ אינו פוגש את הקטע $latex BC$.
בציור יש שני קטעים שאינם נפגשים – $latex AD$ ו-$latex BC$. (גם $latex AC$ ו-$latex BD$ אינם נפגשים). אבל זוהי רק דוגמה, ואילו אנו רוצים להוכיח זאת בצורה כללית. ההוכחה האלגנטית הבאה, של המתמטיקאי הישראלי מיכה פֶּרְלֶס, משתמשת בעקרון הכיסאות המוזיקליים.
פרלס אוהב לתאר את הוכחתו במונחים של כינים שמטילות ביצים על שערות. בכל נקודה עומדת כינה. לכל קטע ("שערה") שהכינה רואה באותה נקודה, הכינה מסתכלת לאורך הקטע, ומטילה עליו ביצה, בסמוך לנקודה שבה היא יושבת, בתנאי הבא: שכאשר היא מסתכלת מן הקצה הזה בכיוון ימין מן הקטע, היא אינה רואה קטע אחר שיוצא מאותה נקודה. "ראייה" היא בזווית קטנה או שווה ל-$latex 180$ מעלות, ו"לא לראות" פירושו שעד לקטע הבא יש זווית גדולה מ-$latex 180$ מעלות. למשל, בדוגמה שלנו הכינה העומדת ב-$latex A$ תטיל ביצה על הקטע $latex AD$, משום שכשהיא מסתכלת בכיוון $latex D$ היא אינה רואה מימינה קטע שיוצא מ-$latex A$. הכינה העומדת ב-$latex B$ תטיל ביצה על ,$latex BC$ הכינה העומדת ב-$latex C$ תטיל ביצה על $latex CA$, והכינה שעומדת ב-$latex D$ תטיל ביצה על $latex BD$. בקצה $latex D$ של הקטע $latex AD$, לעומת זאת, לא תוטל ביצה, משום שהכינה העומדת ב-$latex D$ רואה מימינו של $latex AD$ את הקטע $latex DB$.
הכינה העומדת ב-$latex A$ מטילה ביצה על הקטע $latex AD$, משום שכשהיא מביטה מימין ל-$latex D$ היא אינה רואה קטע – עליה להסתובב ביותר מ-$latex 180$ מעלות עד לקטע הבא, $latex AC$.
ההבחנה המכרעת היא זו: כל כינה מטילה לכל היותר ביצה אחת.
כלומר, הכינה מטילה רק על לכל היותר קטע אחד היוצא מן הנקודה שבה היא עומדת. פירוש הדבר שמכל הקטעים היוצאים מן הנקודה, פרט אולי לאחד, אפשר לראות קטע מצד ימין (ולכן לא תוטל עליהם ביצה). הסיבה פשוטה ביותר: כדי שקטע א' לא יראה מימינו קטע אחר, הזווית בין א' לקטע הבא (עם כיוון השעון) היוצא מאותה נקודה חייבת להיות גדולה מ-$latex 180$ מעלות. אבל לא תיתכנה שתי זוויות גדולות מ-$latex 180$ מעלות באותה נקודה, ולכן ייתכן רק קטע אחד, לכל היותר, שאינו רואה מימינו קטע אחר. ואכן, בדוגמה שבציור, למשל, ליד כל נקודה מוטלת ביצה אחת בדיוק.
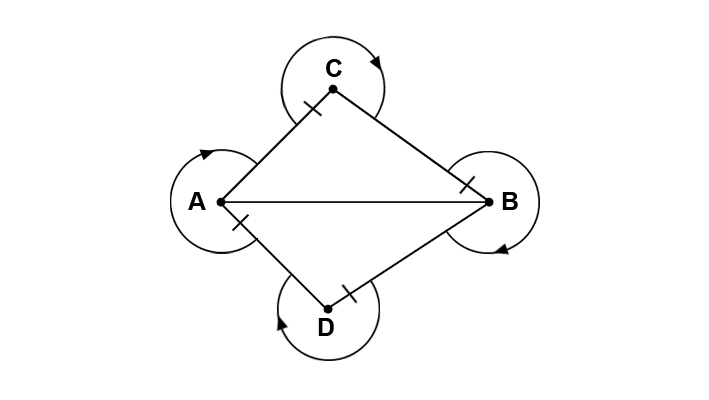
ליד כל נקודה הוטלה ביצה אחת. מכיוון שיש $latex 5$ קטעים ורק $latex 4$ נקודות, יש קטע, $latex AB$, שעליו לא הוטלה ביצה.
עתה נוכל להפעיל את עקרון הכיסאות המוזיקליים. כיוון שליד כל נקודה יש לכל היותר ביצה אחת, מספר הביצים אינו עולה על מספר הנקודות. על פי הנתון, יש יותר קטעים מאשר נקודות, ולכן גם יותר קטעים מאשר ביצים (בדוגמה יש $latex 5$ קטעים, ו-$latex 4$ סימונים). כשנפעיל את עקרון הכיסאות המוזיקליים נקבל שיש קטע (שאותו נציין, נאמר, כ-$latex XY$) שבאף אחד מקצותיו לא הוטלה ביצה (זהו ה"ילד שלא קיבל שלגון"). העובדה שהקטע לא סומן בביצה בקצה $latex X$ משמעה שאפשר לראות מימינו, בנקודה $latex X$, קטע $latex XU$ מן הקטעים הנתונים; העובדה שהוא לא סומן בצד של $latex Y$ פירושה שבנקודה $latex Y$ יש קטע $latex YV$ שנמצא מימינו של $latex XY$. אבל אז הקטעים $latex XU$ ו-$latex YV$ אינם נפגשים!
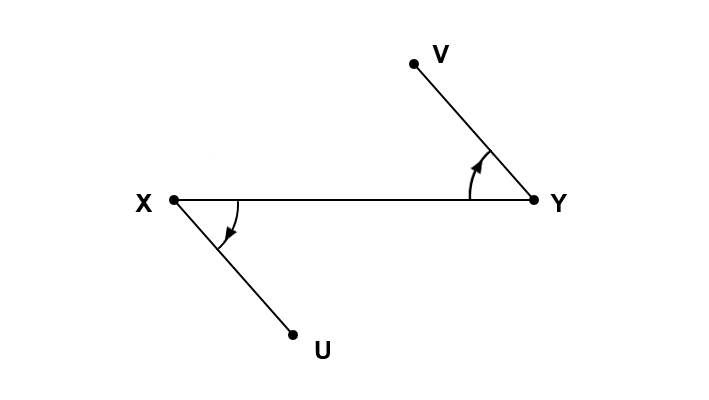
על הקטע $latex XY$ לא הוטלה ביצה. הסיבה: הכינה ב-$latex X$ רואה מימין ל-$latex XY$ את הקטע $latex XU$, והכינה ב-$latex Y$ רואה מימין ל-$latex XY$ את הקטע $latex YV$. הקטעים $latex XU$ ו-$latex YV$ אינם נפגשים, והם אם כן זוג הקטעים המבוקש.
בדוגמה שלעיל, על הקטע $latex AB$ לא הוטלה ביצה. בקצה $latex A$ אין ביצה, משום ש-$latex AD$ נמצא מימינו של $latex AB$, כאשר מסתכלים מכיוון הנקודה $latex A$; בקצה $latex B$ אין ביצה, משום ש-$latex BC$ נמצא מימינו של $latex AB$ כשמסתכלים מן הקצה $latex C$. ואכן, $latex AD$ ו-$latex BC$ אינם נפגשים.
השערת ה-Thrackle
אנה ליזהטוב
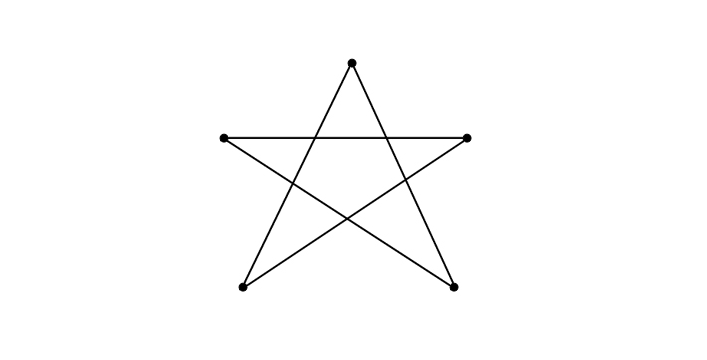
ג'ון קונווי ($latex John Conway$), מתמטיקאי אנגלי שעובד בפרינסטון, הוא אחד המתמטיקאים הידועים של ימינו, וגם אחד הצבעוניים שבהם. הוא בעל כשרון מיוחד לגילוי שיטות אלמנטריות לפתרון בעיות קשות, ולניסוח בעיות אלמנטריות. בסוף שנות ה-$latex 60$ ניסח קונווי השערה שמכלילה את המשפט מן המאמר על הכסאות המוזיקליים, בדבר קיום שני קטעים זרים. ההשערה נשמעת פשוטה למדי, אבל כמו בהרבה מקרים הַפַּשטות הזאת מתעתעת. קונווי הגדיר יצור מתמטי שנקרא "$latex Thrackle$", שמשמעותו (לפחות אליבא דקונווי) "קשר" בגַלית עתיקה. ואכן, היצור הזה הוא מעין ציור של "פלונטר". $latex Thrackle$ הוא ציור המורכב מנקודות, ומעקומים (קווים) המחברים בין הנקודות, שמקיימים את התנאי הבא: כל שני עקומים נפגשים בדיוק בנקודה אחת, ובאותה נקודה הם נחתכים ממש, כלומר אינם משיקים בה. מותר לקטעים להיפגש גם בקצוות שלהם.
זהו $latex Thrackle$, כלומר ציור שבו כל קו פוגש כל קו אחר בדיוק בנקודה אחת. ב- $latex Thrackle$ הזה יש $latex 5$ נקודות ו-$latex 5$ קווים. השערתו של קונווי היא שב-$latex Thrackle$ מספר הקווים אינו יכול לעלות על מספר הנקודות.
השערת ה-$latex Thrackle$ אומרת שמספר הקווים ב-$latex Thrackle$ אינו יכול לעלות על מספר הנקודות. המשפט שהוכחנו בסעיף הקודם אומר שההשערה נכונה כאשר הקווים הם ישרים. ניסחנו אותו אומנם קצת אחרת: "אם יש יותר קטעים מאשר נקודות, יש שני קטעים שאינם נחתכים". אבל זה בבירור שקול ל: "אם כל זוג של קטעים נחתך, אז מספר הקטעים אינו עולה על מספר הנקודות" (כשם ש"אם היום שבת אין תחבורה ציבורית" שקול ל"אם יש תחבורה ציבורית אז היום לא שבת"). השערתו של קונווי היא שתכונת הישרות של הקווים אינה נחוצה – המשפט הזה נכון גם לקווים שאינם ישרים. שימו לב עד כמה הוכחתו של פֶּרלֶס משתמשת בישרותם של הקווים – נראה שלפחות את ההוכחה הזאת קשה יהיה להכליל!
נוסחת קיילי
פרופ' דניאל קלייטמן, תרגם: אליהו לוי
פרופ' דניאל קלייטמן, Daniel J. Kleitman), MIT), ארה"ב
הרצאה שניתנה במועדון המתמטי בטכניון בשנות ה-90 של המאה הקודמת
גרף מורכב משתי קבוצות: הקודקודים, הצלעות. כל צלע היא זוג של קודקודים שונים. אנו נתבונן בגרפים סופיים, ויהי $latex {n}$ מספר אברי קבוצת הקודקודים. לגרף מכוון יש צלעות מכוונות, זאת אומרת צלע היא זוג מסודר של קודקודים, אחד הוא הראש של הצלע והשני הוא הזנב שלה.
מסלול בגרף מהקודקוד $latex {x}$ לקודקוד $latex {y}$ הוא רשימה של צלעות כך ש:
הצלע הראשונה מכילה את $latex {x}$ והצלע האחרונה מכילה את $latex {y}$;
לכל צלע ברשימה יש קודקוד משותף עם הצלע העוקבת לה, וקודקוד אחר משותף עם הצלע הקודמת לה.
גרף נקרא קשיר אם יש מסלול מכל קודקוד לכל קודקוד אחר בו. עץ הוא גרף קשיר שיחדל להיות קשיר אם יוציאו ממנו איזושהי צלע שלו.
(לעץ יש $latex {n-1}$ צלעות: אם לגרף $latex {G}$ אין צלעות אזי כל קודקוד הוא מבודד והגרף מורכב מ $latex {n}$ בלוקים קשירים זרים שכל אחד מהם מורכב מקודקוד אחד. כל צלע שנוספת ל $latex {G}$ או מחברת שני בלוקים ובכך מקטינה את מספר הבלוקים באחד, או נמצאת בתוך בלוק קיים, ובמקרה זה אפשר להשמיטה מ $latex {G}$ בלי לקלקל את הקשירות. אם כך, אחרי הוספת $latex {n-1}$ צלעות הכרחיות-לקשירות לגרף ללא צלעות, הוא ייהפך לקשיר.)
מעגל הוא מסלול מקודקוד לעצמו שמכיל כל קודקוד אחר בשתים מהצלעות שבו לכל היותר. בעץ אין מעגלים: ממעגל אפשר להשמיט צלע בלי להקטין את מידת הקשירות.
$latex {n=6}$
גרף
עץ
מעגל
במאה התשע-עשרה, קיילי $latex Cayley$ שאל וענה על השאלה הבאה: כמה עצים שונים יש עם קבוצה נתונה של $latex {n}$ קודקודים? מאז הופיעו הוכחות רבות של התוצאה שלו. אנו מציגים כאן הוכחה שהיא אולי חדשה.
נראה קודם אם נוכל לנחש את התשובה: כדי לעשות כך נבדוק את המקרים הקטנים: למרבה המזל, עבור ערכים קטנים של $latex {n}$ יש רק מעט צורות שיכולות להיות לעץ, ואפשר לספור כמה עצים יש מכל צורה ללא קושי רב. זה נעשה בציור הבא.
בדרך כלל אפשר לשים את קודקודי צורה על קבוצת $latex {n}$ הקודקודים הנתונים ("לקרוא לקודקודי הצורה בשמות") ב $latex {n!}$ אופנים שונים. אבל, אם לצורה יש סימטריה, אזי אותו עץ יתקבל מ"קריאה כלשהי בשמות" ומתמונתה ע"י פעולת סימטריה. כדי למצוא את מספר העצים השונים מכל צורה יש לחלק את $latex {n!}$ במספר פעולות הסימטריה שיש לצורה (במלים אחרות, בסדר חבורת הסימטריה שלה).
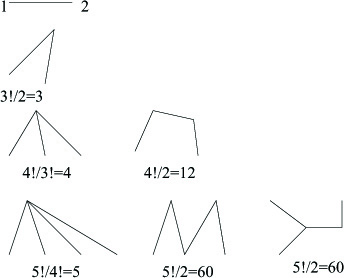
| מס' העצים | $latex {n}$ |
| $latex {1}$ | $latex {n=2}$ |
| $latex {3}$ | $latex {n=3}$ |
| $latex {16}$ | $latex {n=4}$ |
| $latex {125}$ | $latex {n=5}$ |
מוצאים, עבור מספר העצים $latex {c(n)}$ על $latex {n}$ קודקודים: $latex {c(3)=3^1}$, $latex {c(4)=4^2}$, $latex {c(5)=5^3}$, וזה מביא להשערה שהתשובה היא $latex {c(n)=n^{n-2}}$. זה פועל אפילו עבור $latex {n=2}$: $latex {c(2)=1=2^0}$.
נבדוק את $latex {n=6}$, בציור מתוארות הצורות האפשריות:
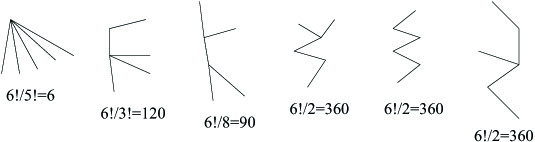הצורות עבור $latex {n=6}$
$latex {360\cdot3+90+120+6=1296=6\cdot6\cdot6\cdot6}$
אם אתם כמוני (וכמו קיילי) , אתם בוודאי כבר משוכנעים שהתשובה הכללית היא $latex {n^{n-2}}$.
זה מה שנוכיח. כדי לעשות זאת, נשאל קודם: מה אנו יודעים שהמספר הזה, $latex {n^{n-2}}$ מונה?
אם נבדוק שוב מקרים קטנים, נראה ש $latex {3=(1+1+1)}$, $latex {4^2=(1+1+1+1)\cdot(1+1+1+1)}$, ובאופן כללי $latex {n^{n-2}}$ הוא מכפלה של $latex {n-2}$ גורמים זהים שכל אחד מהם הוא סכום $latex {n}$ $latex {1}$ -ים.
אפשר להשתמש בחוק הדיסטריבוטיבי (חוק הפילוג) לגבי מכפלה זו פעם אחר פעם עד שהופכים אותה לסכום של מכפלות של אברים בודדים מהגורמים המקוריים. כיון שכל איבר כזה הוא $latex {1}$, כל המכפלות האלה יהיו שוות ל $latex {1}$, ו $latex {n^{n-2}}$ שלנו הוא מספר האברים השונים שמתקבלים מהפעלת חוק הפילוג כאן.
לכן $latex {n^{n-2}}$ מונה את מספר הדרכים השונות לבחור אפשרות אחת מבין $latex {n}$ אפשרויות, $latex {n-2}$ פעמים נבדלות.
אנו רוצים להשתמש בכך, ולהוכיח שאותו מספר מונה גם את מספר העצים.
זו תהיה דרך המחשבה של הוכחתנו:
- $latex {n^{n-2}}$ יכול להיכתב כמכפלה של סכומי $latex {1}$ -ים בסוגריים.
- כל איבר שמתקבל אחרי פתיחת הסוגריים ניתן לתיאור ע"י "פונקציה".
- כל פונקציה כזו קובעת גרף מכוון.
- כל גרף מכוון כזה מתאים לעץ מסוים וכל העצים מתקבלים באופן כזה.
- לכן $latex {n^{n-2}}$ הוא מספר העצים.
אנו הופכים איבר בפיתוח המכפלה לפי חוק הפילוג לפונקציה באופן הבא: איבר מהווה בחירה של מקום אחד בכל אחד מהסוגריים. אם ניתן למקומות השונים שמות $latex {1,2,\ldots,n}$, אזי כל איבר מתאים להתאמת אחד ממספרים טבעיים אלה לכל אחד מהסוגריים. זוהי הפונקציה שמתאימה לאיבר.
הנה דוגמה עם $latex {n=5}$.
$latex \displaystyle 5^3=(1+1+1+\underline{ 1}+1) (1+1+\underline{ 1}+1+1) (1+\underline{ 1}+1+1+1)$
את האיברים המודגשים בקו מתחת אפשר לתאר ע"י ה"פונקציה" או ההתאמה $latex {f(3)=2}$ ,$latex {f(2)=3}$ ,$latex {f(1)=4}$. וכל איבר בפיתוח המכפלה מתואר ע"י פונקציה אחרת.
אפשר לבנות גרף מכוון שמתאים לפונקציה כזו ע"י כך שמפרשים את העובדה $latex {f(1)=4}$, למשל, בתור קיום צלע מכוונת מ $latex {1}$ ל $latex {4}$.
זהו, איפוא, הגרף המכוון שמתאים לפונקציה שבאה מהאיבר לעיל: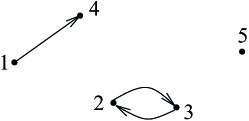 
$latex {f(1)=4, f(2)=3, f(3)=2}$
הגרפים שאנו מקבלים בצורה כזאת אינם עצים. למשל, אלה גרפים מכוונים בעוד שעצים אינם מכוונים. את זה קל לתקן: אפשר לכוון את הצלעות בכל עץ כך שיתכוונו אל הקודקוד $latex {n}$. אז כל עץ נהפך לגרף מכוון; אבל זה עדיין לא נראה כמו הגרפים שלנו.
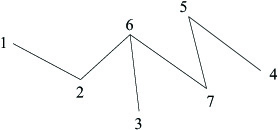
עץ
עץ עם צלעות מכוונות לכיוון $latex {n}$, $latex {n=7}$
כאשר מתייחסים לעצים באופן כזה, הם נבדלים מהגרפים שלנו בשלושה אופנים: בכל אחד מהם יש צלע שיוצאת מ $latex {n-1}$, בעוד שבגרפים שלנו איןאין בהם מעגלים, בעוד שבגרפים שלנו יכולים להיות;. בנוסף לכך, בכל עץ, המכוון באופן זה, יש צלע מכוונת ל $latex {n}$בגרפים שלנו לא חייבת להיות צלע כזו.
כך נהפוך כל אחד מהגרפים שלנו לעץ: נתון גרף כזה $latex {G}$, ניצור מסלול מ $latex {n-1}$ ל $latex {n}$, שעובר דרך כל מעגל ב $latex {G}$ והורס אותו. אם אנו יכולים גם להפוך (לבטל) את התהליך באופן חד-ערכי, אז גמרנו.
איך? נסדר את המעגלים לפי הקודקוד הגדול ביותר בהם (כלומר הקודקוד שהאינדקס המספרי שלו: $latex {1,2,\ldots,n}$ הוא הגדול ביותר) , הגדול ביותר תחילה; ניתן למסלול שלנו להתחיל ב $latex {n-1}$ ולהיכנס לכל מעגל מייד אחרי הקודקוד הגדול ביותר במעגל, ולצאת אל המעגל הבא (או, אם אין יותר, אל $latex {n}$) בקודקוד הגדול ביותר (ובכך תישמט הצלע מהקודקוד הגדול ביותר אל העוקב לו במעגל) . כעת אנו עוברים למעגל בעל הקודקוד השני בגודלו וחוזרים על הבניה, עד שאין יותר מעגלים.
הנה דוגמה כיצד זה נעשה:
$latex {f(1)=4,\,f(2)=3,\,f(3)=2}$
$latex {n-1=4}$
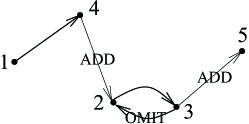
כדי להפוך לעץ:
הוסף צלע מ $latex {n-1}$ לקודקוד שאחרי הגדול ביותר במעגל: $latex {\{4,2\}}$
הוסף צלע מהגדול ביותר במעגל אל המעגל הבא או אל $latex {n}$: $latex {\{3,5\}}$
השמט את הצלע במעגל היוצאת מהקודקוד הגדול ביותר: $latex {\{3,2\}}$
כדי להפוך (לבטל) את הבניה - כדי לקבל את $latex {G}$ מהעץ המתאים $latex {T}$, מצא את המסלול מ $latex {n-1}$ ל $latex {n}$ ב $latex {T}$; הקודקוד הגדול ביותר במסלול זה מסמן את קצה המעגל הראשון ב $latex {G}$. בנה מחדש מעגל זה, השמט את הצלע שיוצאת מ $latex {n-1}$, ועבור למעגל הבא; בנה אותו מחדש באופן דומה, והמשך עד שיצרת את $latex {G}$.
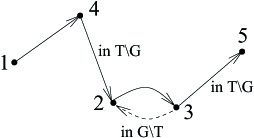
$latex {G\setminus T}$ מורכב מצלע מכל מעגל - זו שיוצאת מהקודקוד הגדול ביותר במעגל.
$latex {T\setminus G}$ מורכב מצלע מ $latex {n-1}$ למעגל הראשון, צלעות מהקודקוד הגדול ביותר בכל מעגל אל העוקב לגדול ביותר במעגל הבא, ולבסוף צלע אל $latex {n}$. הוכחנו את נוסחת קיילי. אם אתם רוצים לשכנע את עצמכם ששיקולים אלה פועלים, נסו לצייר כמה עצים ולהפוך אותם לגרפים, לפונקציות ולאיברים בפיתוח של $latex {n^{n-2}}$ וללכת גם בדרך ההפוכה. התהליך של המרת מעגלים במסלול כמו שאנו עושים זאת כאן מזכיר לי עשיית מחרוזת עם חרוזים מסודרים לפי הגודל.
הערה נוספת: הפונקציה $latex {(x_1+x_2+\cdots+x_n)^{n-2}}$, כאשר מפתחים אותה לפי חוק הפילוג (החוק הדיסטריבוטיבי) , מורכבת מ $latex {n^{n-2}}$ איברים, אחד עבור כל גרף $latex {G}$, ולכן אחד עבור כל עץ, בדיוק כמו לעיל, פרט לכך שהאיברים אינם כולם $latex {1}$. באיבר שנתרם ע"י עץ מסויים יש חזקה $latex {x_j}^k $ אם $latex {j}$ נלקח $latex {k}$ פעמים בבניית האיבר המתאים מחוק הפילוג; זה אומר שהערכיות הנכנסת של הקודקוד $latex {j}$ ב $latex {G}$ היא $latex {k}$.
כל ערכיות ב $latex {T}$ היא בדיוק ב $latex {1}$ יותר מהערכיות הנכנסת של אותו קודקוד ב $latex {G}$לכן הפונקציה לעיל היא הסכום על העצים של המכפלה עבור אינדקסים $latex {j}$ בין $latex {1}$ ו $latex {n}$ של $latex {x_j}$ מועלה לחזקה שהיא ערכיות הקודקוד $latex {j}$ ב $latex {T}$ פחות $latex {1}$. בסימון מתמטי זה נכתב כך:
$latex \displaystyle \prod_{j=1}^n \left((x_j)^{d_j(T)-1}\right)$
הטענה האומרת ששתי ישויות אלה הן שוות היא הצורה החזקה המקובלת של נוסחת קיילי.
יש תריסרי הוכחות שונות לנוסחת קיילי, אבל כולן נראות קצת קשות יותר מזו שהבאנו. ההוכחה הקרובה לה ביותר ברוחה היא של $latex Chen$.
חידות
דניאל לובזנס
דבר העורך: בחודש שעבר חל "יום הפאי" – כידוע היחס בין הקף המעגל לקוטרו הוא המספר האי-רציונלי פאי $latex \pi = 3.1415\dots\dots$ בצורת כתיבת התאריכים האמריקאית $latex 3/14$ הוא ה $latex 14$ במרס שזהו יום הולדתו של אלברט איינשטיין ומצוין כיום המדע (ראו ערך).
שתי חידות יעסקו בחלוקת הפאי (במובן של העוגה) והשלישית תעסוק במעגלים.
לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 26.4.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1– איך לחלק את הפאי?
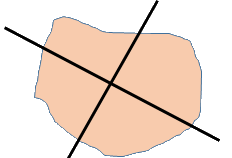
עוגת פאי ניתנת לתיאור ע"י צורה דו ממדית כלשהיא. האם אפשר לחלק אותה ל$latex 4$ חלקים שווים בשטחם ע"י שני ישרים הניצבים זה לזה?
חידה 2– איך לחלק את העוגה?
לא תמיד חלוקה של עוגה לשני חלקים שווים בשטחם (לעוגה דו ממדית) או בנפחם/משקלם (לעוגה תלת ממדית) היא חלוקה "צודקת". לעוגה יכולים להיות חלקים נחשקים יותר (צימוקים, ציפוי שוקולד….) ונחשקים פחות (אזורים שנחרכו…) ולכן קשה לחלקה לשניים בצורה שתבטיח שכל אחד ממקבלי החלקים לא ירגיש מקופח. בכל זאת אפשר לחלק עוגה באופן "צודק" בין שני אנשים בצורה הבאה:
הראשון חותך את עוגה לשני חלקים בצורה הנראית לו "צודקת", כלומר הוא לא ירגיש מקופח אם יקבל כל אחד מהחלקים. עכשיו נתן לשני לבחור את החלק שהוא רוצה בו, ובכך נבטיח שגם הוא לא ירגיש מקופח ולכן החלוקה תהיה "צודקת". יש לתת את הדעת לכך שצורה זו של חלוקה מותירה כל צד שמח בחלקו גם העדפותיהם שונות.
איך נתן לחלק עוגה בצורה "צודקת" (במובן זה שאף אחד מהמשתתפים לא ירגיש מקופח) בין שלושה אנשים?
חידה 3– מסלול ?
שני מעגלים, האחד בעל מחצית הרדיוס מהשני, נמצאים אחד בתוך השני, משיקים זה לזה –כמתואר בציור:
כאשר המעגל הפנימי מתגלגל בלי להחליק בתוך המעגל החיצוני, ומשלים $latex 2$ סיבובים עד שהוא חוזר למקומו הנוכחי, איך יראה המסלול שתתווה נקודה כלשהיא $latex A$?
רמזים לחידות מגיליון מרס 2015
חידה 1– עקומות על תפוחי אדמה? – תארו לעצמכם את שני תפוחי האדמה החותכים אחד את השני.
חידה 2– מה אורך החוט? - מצאו קשר כללי בין ארכי צלעות של רבוע שאלכסוניו נצבים – ראו את חידת קידוח הנפט מינואר 2015
חידה 3– הזיקיות? – חישבו מודולו $latex 3$.
פתרון החידות גיליון פברואר 2015
חידה 1– סכומים של ספרות
נסתכל על סכום הספרות מ $latex 0$ עד $latex N=999,999$. נראה שאם נסכם זוגות מספרים $latex m$ ו$latex N-m$ , ($latex 0$ ו-$latex 999,999$ ,$latex 1$ ו-$latex 999,998$ ,$latex 2$ ו-$latex 999,997 $ וכו') סכום כל זוג הוא $latex 999,999$ סכום ספרותיו $latex 9*6=54$. יש $latex 500,000$ זוגות כאלה ולכן סכום הספרות של המספרים מ$latex 0$ עד $latex 999,999$ הוא $latex 54*500,000=27,000,000$ וסכום הספרות של $latex 1,000,000$ הוא $latex 1$ ולכן הסכום המבוקש הוא: 27,000,001.
חידה 2– מרכזי ריבועים על גבי מקבילית
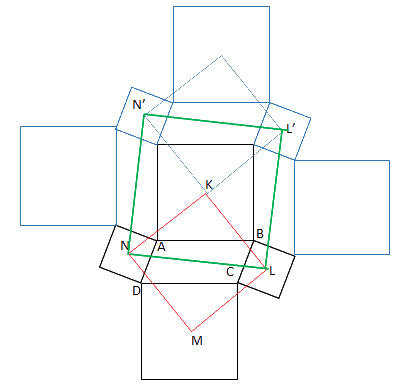
אפשר כמובן להוכיח באמצעות משולשים חופפים כפי שהוצע ברמז. העדפתי להביא פתרון שמסתמך על סימטריה. מעתיקים את הצורה הבסיסית ומשכפלים אותה עוד $latex 3$ פעמים סביב הרבוע שמרכזו ב$latex K$. בשל הסימטריה $latex N’L’LN$ הוא רבוע שמרכזו ב $latex K$, ולכן $latex KN=KL$ והזווית $latex NKL$ היא זווית ישרה (אלכסוני הרבוע נצבים זה לזה, זהים באורכם, וחוצים זה את זה) ולכן $latex KLMN $ גם הוא רבוע.
חידה 3– סכום של הופכיים
מאחר ואין ל $latex a_i$ גורמים שווים או גדולים מ $latex 5$ , רק $latex 2$ ו $latex 3$ הם הגורמים הראשוניים שלו. כלומר: $latex a_i=2^l*3^m$ כאשר $latex 0 \le l \le L, 0 \le m \le M$ (הגבול העליון נובע מכך שיש מספר סופי של מספרים $latex a_i$)
נסמן באותיות $latex A$ ו $latex B$ את הסכומים הבאים:
$latex A=\sum\limits_{i=0}^{i=L} \frac{1}{2^i} = 1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\dots+\frac{1}{2^L}$
$latex B=\sum\limits_{i=0}^{i=M} \frac{1}{3^i} = 1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+\dots+\frac{1}{3^M}$
$latex A$ ו $latex B$ הם סכומים של סדרות הנדסיות וניתן לחשב את ערכן:
$latex A=\frac{1-(\frac{1}{2})^{L+1}}{1-(\frac{1}{2})} < \frac{1}{1-(\frac{1}{2})}=2$
$latex B=\frac{1-(\frac{1}{3})^{M+1}}{1-(\frac{1}{3})} < \frac{1}{1-(\frac{1}{3})}=\frac {3}{2}$
אם נסתכל במכפלה AB נראה כי אחרי פתיחת סוגריים מופיעים בה כל האברים מהצורה : $latex \frac{1}{a_i} = \frac {1}{2^l*3^m}$
כאשר $latex a_i=2^l*3^m$ כאשר $latex 0 \le l \le L, 0 \le m \le M$. כלומר:
$latex S=\sum\limits_{i=0}^{i=n}\frac{1}{a_i} =\frac{1}{a_1}+\frac{1}{a_2}+\frac{1}{a_3}+\dots+\frac{1}{a_n}< A*B< 2*\frac{3}{2} = 3$
מ.ש.ל.
שמות הפותרים נכונה את החידות מגיליון מרץ 2015
משה דוידוביץ' – חידה 3
רועי סיני מכפר האורנים, כיתה ח'3 בבי"ס אור – כל החידות!