נטגר גליון 15

---

דבר העורך

רון אהרוני

מה זו מתמטיקה? שאלה קשה באמת. בגיליון הזה תמצאו פורום לדיון בשאלה הזאת (כאן) - נשמח לתשובותיכם. אבל ברור דבר אחד: מתמטיקה עושה הפשטות של מה שקורה בעולם. וככל שמתקדמים במתמטיקה, מידת ההפשטה גדולה יותר. מושג המספר הוא כבר הישג גדול של ההפשטה האנושית: משלושה תפוחים, שלושה חתולי ושלושה ילדים יצר האדם את המושג המופשט של המספר $latex {3}$. מאחורי ההפשטה הזאת עומדת ההבנה שמבחינת הפעולות, לא חשוב מה מונים: אם תצרפו $latex {3}$ עפרונות ל-$latex {2}$ עפרונות תקבלו $latex {5}$ עפרונות, ואם תצרפו $latex {3}$ תפוחים ל-$latex {2}$ תפוחים תקבלו $latex {5}$ תפוחים. לכן אפשר לכתוב בקיצור $latex {3+2=5}$. בשלב ההפשטה הבא, האלגברה, מדברים כבר על מספרים כלליים. בגיליון הזה נספר על מושג מופשט מאוד: חבורה. חבורה היא קבוצה עם פעולה, שמקיימת תכונה פשוטה מאוד: הפיכות. יש פעולות הפיכות בחיים - אם הלכת צעד צפונה אתה יכול לחזור לנקודת המוצא אם תלך צעד דרומה. יש גם פעולות לא הפיכות - למשל, אם בטעות שמתם מלח בתה במקום סוכר, יהיה לכם קשה מאוד להפוך את הפעולה הזאת. כנראה תצטרכו להכין כוס תה מחדש. ובכן, חבורה היא קבוצה עם פעולה הפיכה. למשל, החיבור במספרים השלמים הוא הפיך - הפעולה ההפוכה היא חיסור. כפל במספרים הממשיים בלי $latex {0}$ גם הוא הפיך. הפעולה ההפוכה היא חילוק. במספרים השלמים הכפל אינו פעולה הפיכה, במובן זה שהחילוק, הפעולה הטבעית ההפוכה, אינו מוגדר לכל שני מספרים. למשל, $latex {1:2}$ אינו מוגדר בשלמים.

בגיליון הזה נלמד על המושג הזה, של החבורה. חבורות הן דבר שימושי מאין כמותו. תורת החלקיקים האלמנטריים, למשל, מבוססת על חבורות. בגיליון הזה נלמד על שימוש אחד של החבורות: מציאת שלשות פיתגוריות. במאמר של אמנון יקותיאלי מאוניברסיטת בן גוריון נעשה קישור יפה בין השלשות האלה, מספרים מרוכבים ומושג החבורה.

---

חבורות - חלק ב

אנה ליזהטוב

6. סכום ישר של חבורות

קבוצת הוקטורים במישור, עם פעולת החיבור, גם היא חבורה. אבל כידוע אפשר לזהות את קבוצת הוקטורים במישור עם נקודות במישור - כל נקודה מזוהה עם הוקטור מן הראשית אליה. בייצוג הזה, החיבור הוא קואורדינטה-קואורדינטה (למשל $latex {(2,3)+(10,20)=(12,23)}$). הבנייה הזאת, של זוגות של איברים עם פעולה קואורדינטה-קואורדינטה, היא כללית. כך מגדירים את $latex {(\mathbb{R}^2,+)}$, $latex {(\mathbb{Q}^2,+)}$ (הראשון הוא המישור הממשי, השני המישור של המספרים הרציונליים).

באופן כללי, בהינתן שתי חבורות (שמותר להן להיות גם שוות - כך היה במקרים לעיל) $latex {(G, \cdot)}$ ו-$latex {(H, \cdot)}$, (בשתיהן השתמשנו באותו סימן פעולה, אבל זה לא חייב להיות כך), הסכום הישר שלהן $latex {G \oplus H}$ הוא אוסף הזוגות $latex {(g,h),~g \in G, ~h \in H}$ עם הפעולה: $latex {(g,h)\cdot (g',h')=(g\cdot g',h\cdot h')}$.

קל לראות שאם $latex {G}$ ו-$latex {H}$ סופיות, אז $latex {|G \bigoplus H|=|G| \times |H|}$. משום כך משתמשים לפעמים בסימון $latex {G \times H}$ לסכום הישר, ואז קוראים לו "מכפלה".

עכשיו אתם מבינים את מקור השם $latex {\mathbb{R}^2}$ - זוהי מכפלת $latex {\mathbb{R}}$ בעצמו, אם כן זוהי חזקה שנייה שלו.

7. איזומורפיזם

כבר הזכרנו את מושג האיזומורפיזם. כאמור, "איזומורפי" פירוש "שווה צורה". באופן כללי שני גופים נקראים "איזומורפיים" אם הם למעשה שווים כשרק שינוי שמות האיברים מפריד ביניהם. "איזומורפיזם" מוגדר לכל מבנה מתמטי. הנה ההגדרה במקרה של חבורות:

הגדרה 7.1

שתי חבורות $latex {G}$ ו-$latex {H}$ נקראות איזומורפיות אם יש פונקציה

$latex {\phi: G \rightarrow H}$ חד-חד ערכית ועל ששומרת על הפעולה, כלומר, $latex {\phi(gh)=\phi(g)\phi(H)}$.

(הערה: פעמים רבות נשתמש באות $latex {\phi}$ לציון פונקציה. הסיבה היא שזוהי ה-$latex {f}$ היוונית.)

פירוש הדבר ששתי החבורות נראות אותו דבר, פרט לקריאה בשמות שונים. במקום להסביר, הנה דוגמה: $latex {\mathbb{Z}_2}$, שהיא $latex {\{0,1\}}$ עם פעולת החיבור, איזומורפית ל-$latex {\{1,-1\}}$ עם פעולת הכפל. הפונקציה שמראה זאת היא:

$latex {\phi(0)=1,~\phi(1)=-1}$.

כל חבורה היא איזומורפית לעצמה (כמובן - הרי כל דבר הוא "שווה צורה" לעצמו), כשהאיזומורפיזם הוא הזהות: $latex {\phi(x)=x}$. זהו האיזומורפיזם ה"טריוויאלי" (כלומר, פשוט).

עובדה מעניינת: שתי חבורות יכולות להיות איזומורפיות עם יותר מאיזומורפיזם אחד. במיוחד, חבורה יכולה להיות איזומורפית לעצמה באיזומורפיזם לא טריוויאלי.

תרגיל:

הוכיחו שכל חבורה איזומורפית לעצמה והראו דוגמה בה קיים יותר מאיזומורפיזם אחד מחבורה לעצמה.

פתרון:

נסתכל על העתקת הזהות $latex {Id:G\rightarrow G}$ כך ש- $latex {Id(a)=a}$ לכל $latex {a\in G}$.

ברור שזו העתקה חח"ע ועל. בנוסף מתקיים $latex {Id\left(ab\right)=ab=Id\left(a\right)Id\left(b\right)}$ כלומר זו העתקה ששומרת על הכפל ולכן היא איזומורפיזם.

דוגמה לאיזומורפיזם שאינו הזהות:

נגדיר$latex {\phi:\mathbb{Z}_{4}\rightarrow\mathbb{Z}_{4}}$ שמקיימת: $latex {\phi\left(1\right)=3,\phi\left(2\right)=2,\phi\left(3\right)=1,{\phi}\left(0\right)=0}$, זו העתקה חח"ע ועל ששומרת על הפעולה שאינה הזהות.

8. חבורות ציקליות

איבר $latex {a}$ בחבורה $latex {G}$ מסדר $latex {n}$ נקרא "יוצר" של $latex {G}$ אם $latex {G=\{a^0=e_G, a, a^2, a^3, \ldots ,a^{n-1}\}}$.

טענה: אם $latex {a}$ יוצר של חבורה $latex {G}$ מסדר $latex {n}$ אז $latex {a^n=e}$.

הוכחה: נניח שלא. מכייון שעל פי ההנחה כל איבר הוא מן הצורה $latex {a^k}$ ל $latex {k<n}$ כלשהו, נובע ש: $latex {a^n = a^k}$ לאיזשהו $latex {k<n}$. ההנחה $latex {a^n \neq e}$ משמעה ש-$latex {k>0}$. אבל אז צמצום נותן לנו $latex {a^{n-k}=e}$, מה שאינו אפשרי: ההנחה היא שעבור $latex {0 <i <n}$ כל איבר $latex {a^i}$ הוא איבר שונה מ-$latex {e}$.

חבורה שיש לה יוצר נקראת "ציקלית". התרגיל הבא הוא שימוש פשוט בהגדרה:

תרגיל 8.1 הראו ש-$latex {a}$ הוא יוצר של החבורה אם הסדר שלו שווה לסדר החבורה.

אם כן, אפשר להגדיר "חבורה ציקלית" כך:

הגדרה 8.2 חבורה היא ציקלית אם יש בה איבר שסדרו כסדר החבורה.

תהא $latex {G}$ חבורה ציקלית מסדר $latex {n}$, עם יוצר $latex {a}$. מכיוון ש-$latex {a^n=e}$, לכל מספר $latex {k}$ מתקיים $latex {a^{kn}=(a^n)^k=e}$. לכן לכל $latex {k}$ ו-$latex {\ell}$ מתקיים $latex {a^{kn+\ell}=a^\ell}$. שפירושו הוא ש-$latex {a^m=a^{m\mod(n)}}$

($latex {m\mod(n)}$ מציין את השארית של $latex {m}$ בחלוקה ב-$latex {n}$. $latex {mod}$ הוא "מודולו".)

כמסקנה מקבלים:

משפט 8.3 חבורה ציקלית $latex {G}$ מסדר $latex {n}$ איזומורפית ל-$latex {(\mathbb{Z}_n,+)}$.

הוכחה: יהא $latex {a}$ יוצר של $latex {G}$. נגדיר איזומורפיזם: $latex {\phi: \mathbb{Z}_n \rightarrow G}$ על ידי $latex {\phi(i)=a^i}$. נראה ש-$latex {\phi}$ שומר על הפעולה. לפי ההגדרה

$latex \displaystyle \phi(i+j)=a^{i+j}=a^{i+j \mod(n)}$

מצד שני,

$latex \displaystyle \phi(i)\cdot \phi(j)=a^i\cdot a^{j}=a^{i+j}$

ולפי ההבחנה לעיל

$latex \displaystyle a^{i+j}=a^{i+j \mod(n)}$

ולכן

$latex \displaystyle \phi(i+j)=\phi(i)\cdot \phi(j)$

כפי שנדרש מאיזומורפיזם. שתי התכונות האחרות שנדרשות מאיזומורפיזם, חד חד ערכיות ועל, נובעות ישר מן ההגדרה - האם תוכלו להסביר אותן לעצמכם?

הנה מסקנה פשוטה:

$latex {\mathbb{Z}_2 \bigoplus \mathbb{Z}_3 \cong \mathbb{Z}_6}$.

הוכחה -כדי להוכיח את הטענה, נראה ש-$latex {\mathbb{Z}_{2}\oplus\mathbb{Z}_{3}}$ היא חבורה ציקלית מסדר $latex {6}$.

שימו לב, שכאשר הפעולה היא פעולת חיבור, אז $latex {g^{k}}$ הכוונה היא $latex {k}$ פעמים להפעיל את הפעולה חיבור, כלומר $latex {kg}$.

ניקח $latex {g=\left(1,1\right)}$, אז $latex {2g=\left(0,2\right)}$, $latex {3g=\left(1,0\right)}$, $latex {4g=\left(0,1\right)}$, $latex {5g=\left(1,2\right)}$, $latex {6g=\left(0,0\right)}$.

קיבלנו את כל אברי החבורה ולכן זוהי חבורה ציקלית והיא איזומורפית ל-$latex {\mathbb{Z}_{6}}$.

המשפט הזה הוא מקרה פרטי של משפט כללי:

משפט 8.4 אם $latex {k, \ell}$ הם מספרים זרים (כלומר אין להם מחלק משותף גדול מ-1) אז $latex {\mathbb{Z}_k \bigoplus \mathbb{Z}_\ell \cong \mathbb{Z}_{k\ell}}$.

נוכיח זאת בהמשך.

תרגיל:

מצאו את כל היוצרים של $latex {\mathbb{Z}_{10}}$.

פתרון:

$latex {\mathbb{Z}_{10}=\left\{ 0,1,2,\dots,9\right\} }$.

היוצרים של $latex {\mathbb{Z}_{10}}$ הם כל האיברים $latex {a\in\mathbb{Z}_{10}}$ כך ש- $latex {o\left(a\right)=10}$.

כיוון שהפעולה היא חיבור, סדר של איבר $latex {a}$ הוא המספר הטבעי המינימלי $latex {k}$ כך ש-$latex {ka\equiv0\left(mod10\right)}$ ($latex {ka}$ מתחלק ב-$latex {10}$) והיוצרים הם אלה שה- $latex {k}$ המינימלי הוא $latex {10}$.

נעבור על אברי החבורה אחד אחד:

$latex {1\cdot0=0}$ ולכן $latex {o\left(0\right)=1}$, $latex {k\cdot1\equiv o\left(mod10\right)}$ גורר $latex {k=10}$ .

$latex {k\cdot2\equiv0}$ גורר $latex {k=5}$, $latex {k\cdot3\equiv0}$ גורר $latex {k=10}$, $latex {k\cdot4\equiv0}$ גורר $latex {k=5}$

$latex {k\cdot5\equiv0}$ גורר $latex {k=2}$, $latex {k\cdot6\equiv0}$ גורר $latex {k=5}$, $latex {k\cdot7\equiv0}$ גורר $latex {k=10}$

$latex {k\cdot8\equiv0}$ גורר $latex {k=5}$, $latex {k\cdot9\equiv0}$ גורר $latex {k=10}$.

לכן היוצרים הם $latex {1,3,7,9}$ וניתן לשים לב שאלה בעצם כל המספרים הזרים ל-$latex {10}$.

הערה:

זה נכון באופן כללי: כל היוצרים ל $latex {\mathbb{Z}_{n}}$ אלה בעצם כל המספרים שזרים ל-$latex {n}$.

תרגיל:

הוכיחו שבחבורה אבלית סופית, סדר של איבר מחלק את הסדר של החבורה.

פתרון:

בתרגול הקודם הוכחנו שבחבורה אבלית סופית $latex {G}$, לכל $latex {a\in G}$ מתקיים $latex {a^{n}=e}$.

נסמן $latex {o\left(a\right)=k}$ , כלומר $latex {a^{k}=e}$ ו-$latex {k}$ הוא המספר הטבעי המינימלי שמקיים זאת.

לכן $latex {n\geq k}$. מחלוקה עם שארית, קיימים $latex {d,r}$ כך ש- $latex {n=dk+r}$ כאשר $latex {r<k}$.

לכן $latex {e=a^{n}=a^{dk+r}=a^{dk}\cdot a^{r}=\left(a^{k}\right)^{d}a^{r}=e^{d}a^{r}=a^{r}}$, אם $latex {r>0}$ אז זו סתירה למינימליות של $latex {k}$, לכן בהכרח $latex {r=0}$, כלומר $latex {n=dk}$ ולכן $latex {k|n}$.

בהמשך נוכיח שהמשפט הזה נכון גם לחבורות לא אבליות.

9. תת חבורות

תת קבוצה של חבורה שהיא בעצמה חבורה, לגבי אותה פעולה כמו של החבורה כולה, נקראת "תת חבורה". למשל, הקבוצה $latex {\{e\}}$ שמכילה רק את האיבר האדיש היא תת חבורה של כל חבורה. גם החבורה כולה היא תת חבורה של עצמה. שתי אלה נקראות "תת חבורות טריוויאליות".

דוגמה: לחבורה $latex {\mathbb{Z}_4=\{0,1,2,3\}}$ יש תת חבורה מסדר $latex {2}$, הלא היא $latex {\{0,2\}}$. תת חבורה צריכה להיות סגורה לגבי פעולת החבורה, וגם לגבי היפוך. כלומר, כדי ש- $latex {H}$ תהיה תת חבורה של $latex {G}$ נחוץ שאם $latex {a,b \in H}$ אז $latex {ab \in H}$ וכן שאם $latex {a \in H}$ אז $latex {a^{-1}\in H}$.

10. $latex {(\mathbb{Z}_p^*,\cdot)}$ ו-$latex {U_n}$

האם $latex {\mathbb{Z}_n}$ היא חבורה גם לגבי הכפל? יש יחידה (איבר אדיש), הלא היא המספר $latex {1}$, אבל לא לכל איבר יש הופכי. למשל, ל-$latex {0}$ אין הופכי.

מה יקרה אם נזרוק את $latex {0}$? גם אז לא תמיד יש הופכי. למשל, ב-$latex {\mathbb{Z}_6}$ לאיברים $latex {2}$ ו-$latex {4}$ אין הופכיים, כי כל כפולה שלהם היא זוגית, וגם לאיבר $latex {3}$ אין הופכי, כי כל כפולה שלו מתחלקת ב-$latex {3}$.

אבל כאשר $latex {n}$ ראשוני אכן זריקת ה-$latex {0}$ עוזרת. למספר ראשוני $latex {p}$ נסמן ב-$latex {\mathbb{Z}_p^*}$ את קבוצת האיברים ב-$latex {\mathbb{Z}_p}$ כשזורקים ממנו את ה-$latex {0}$. כלומר - אלה הם האיברים $latex {1,2,\ldots,p-1}$.

משפט 10.1

א. מכפלה של כל שני איברים ב-$latex {\mathbb{Z}_p^*}$ נמצאת ב-$latex {\mathbb{Z}_p^*}$ (כלומר היא שונה מ-$latex {0}$).

ב. לכל איבר ב-$latex {\mathbb{Z}_p^*}$ יש הופכי לגבי הכפל.

 

הוכחה א' נובע מכך שמכפלת שני מספרים שאין להם הגורם $latex {p}$ אינה מתחלקת ב-$latex {p}$ (דבר שאינו נכון למספר לא ראשוני. למשל, $latex {2}$ אינו מתחלק ב-$latex {6}$, וגם $latex {3}$ אינו מתחלק ב-$latex {6}$, אבל מכפלתם כן מתחלקת ב-$latex {6}$).

הוכחת ב': תהא $latex {a}$ שארית. אם נכפול את $latex {a}$ בכל $latex {p-1}$ איברי $latex {\mathbb{Z}_p^*}$ נקבל, לפי חוק הצמצום, $latex {p-1}$ תוצאות שונות. אחת מהן חייבת להיות $latex {1}$.

משמעות המשפט הזה היא ש-$latex {(\mathbb{Z}_p^*,\cdot)}$ היא חבורה.

את התוצאה הזאת אפשר להכליל גם ל-$latex {n}$ שאינו ראשוני - אמנם לא לכל החבורה $latex {\mathbb{Z}_n^*}$, אלא לחלק ממנה. נסמן ב-$latex {U_n}$ (ה-$latex {U}$ הוא קיצור של $latex {units}$) את השאריות הזרות ל-$latex {n}$. למשל, $latex {U(10)=\{1,3,7,9\}}$ (כל שאר $latex {5}$ השאריות, $latex {2,4,5,6,8}$ אינן זרות ל-$latex {10}$). אזי בדיוק אותו משפט נכון:

משפט 10.2

א. מכפלה של כל שני איברים ב-$latex {U_n}$ נמצאת ב-$latex {U_n}$ (כלומר היא זרה ל-$latex {n}$).

ב. לכל איבר ב-$latex {U_n}$ יש הופכי לגבי הכפל.

 

המסקנה היא ש-$latex {(U_n, \cdot)}$ היא חבורה לגבי הכפל.

---

חבורות - חלק א

אנה ליזהטוב

1. מה זו אלגברה

אתם לומדים אלגברה מזה הרבה שנים. קרוב לוודאי שמכיתה ז'. האם אתם חושבים שאתם יכולים להגדיר מהי? מה זו אלגברה?

לשאלה הזאת אין תשובה אחת ברורה. אבל באופן כללי הנה התשובה: האלגברה עושה הפשטה של מושג המספר.

צריך להבין: מספרים הם כבר בעצמם עניין מופשט. חישבו: מה זה $latex {3}$? זוהי הפשטה משלושה תפוחים, שלושה עפרונות ושלושה אנשים. המתמטיקה "גילתה" שמבחינה חשבונית כולם מתנהגים אותו דבר, למשל אם $latex {3}$ תפוחים ועוד $latex {2}$ תפוחים הם $latex {5}$ תפוחים אז גם $latex {3}$ עפרונות ועוד $latex {2}$ עפרונות הם $latex {5}$ עפרונות. אפשר לחסוך (כל הפשטה חוסכת מאמץ!) ולכתוב באופן כללי: $latex {3+2=5}$. זה יהיה נכון גם לאנשים, ולכסאות, וזה יהיה נכון גם מחר.

האלגברה הוא שלב ההפשטה הבא: דיבור על מספרים כלליים. לשם כך המציאו שמות כלליים - ה-$latex {x}$ וה-$latex {y}$ המפורסמים. בעזרתם אפשר לכתוב חוקים כלליים, כמו $latex {(x+1)^2=x^2+2x+1}$. זהו חוק שנכון לכל מספר.

זוהי האלגברה התיכונית. היא פותחה על ידי הערבים, החל מן המאה ה-$latex {11}$, והובאה לאירופה על ידי המתמטיקאי האיטלקי פיבונצ'י. המשכו של הסיפור הוא באלגברה הליניארית, שאותה המציאו במאה התשע עשרה. תפגשו בה כשתגיעו לאוניברסיטה. כמבוא של מבוא, אספר לכם שזהו כלי, שבין השאר מאפשר גישה מופשטת לפתרון מערכות של משוואות ליניאריות (כלומר משוואות שבהן כל הנעלמים מופיעים בחזקה $latex {1}$). מדוע גם לה קוראים "אלגברה"? לא רק בגלל זה שהיא מדברת על משוואות, אלא גם משום שהיא צעד נוסף של הפשטה: לא דיבור על מספרים כלליים, אלא על מבנים כלליים. קבוצות של איברים עם פעולות, ממש כמו שהמספרים הממשיים הם קבוצה של איברים עם פעולות.

בסוף המאה השמונה עשרה ובתחילת המאה התשע עשרה התחילו לחקור מבנה כללי אחר, שמחקה בתכונותיו את המספרים השלמים. זוהי החבורה. המפתחים הראשונים שלו היו הצרפתים לגרנז' וגלואה, והנורווגי אבל ($latex {Abel}$). אבל וגלואה מתו בגילים צעירים מאוד - אבל מת משחפת בגיל $latex {26}$ וגלואה בגיל $latex {20}$, בדו קרב. הם השתמשו בחבורות כדי לחקור פתרונות של משוואות ממעלות גבוהות. בעזרת הכלי הזה הם הוכיחו, למשל, שאי אפשר למצוא פתרון כללי למשוואות ממעלה $latex {5}$ או יותר. מאז המושג הזה התברר כשימושי בהרבה מאוד תחומים. למשל, תורת החלקיקים האלמנטריים מבוססת עליו.

2. חבורות

חבורה היא קבוצה עם פעולה אחת. כמו השלמים, עם פעולת החיבור (בינתיים אין מדברים על פעולה נוספת, כמו כפל). אתם בוודאי תוהים: אבל בשלמים יש גם חיסור! איך אפשר לדבר על חיבור בלי לדבר על חיסור! ובכן, יהיה לנו חיסור. אבל אנחנו נבטא אותו בעזרת החיבור, ובעזרת מה שמקביל ל"מינוס של מספר". במקום $latex {3-5}$ נכתוב $latex {3+(-5)}$. הנה ההגדרה הפורמלית.

הגדרה 2.1 חבורה ($latex {group}$) היא קבוצה $latex {G}$ עם פעולה שאפשר לסמן אותה ב-$latex {\cdot}$ או ב-$latex {\times}$ או ללא סימון בכלל (ואז היא נקראת "כפל"), או ב-$latex {+}$ (ואז היא נקראת "חיבור"), שמקיימת שלושה תנאים:

1. אסוציאטיביות: לכל שלושה איברים $latex {a,b,c}$ מתקיים $latex {(ab)c=a(bc)}$ (כלומר - אין זה חשוב באיזה סדר מבצעים את הפעולות. שימו לב - ייתכן מאוד שסדר האיברים כן משנה, כלומר $latex {ab\neq ba}$.)
2. קיום איבר אדיש, שמסומן ב-$latex {e}$ (מן המילה הגרמנית $latex {egal}$, שמקורה צרפתי, ופירושה "אותו דבר", או "אדיש"), שכפל בו אינו משנה את האיבר. כלומר, לכל איבר $latex {x}$ מתקיים $latex {xe =ex=x}$. (מכיוון שהפעולה אינה דווקא קומוטטיבית, צריכים לציין במפורש שגם $latex {xe =x}$ וגם $latex {ex=x}$.)
3. קיום הפיך: לכל איבר $latex {x}$ קיים הופכי מימין, איבר $latex {g}$ ש-$latex {xg=e}$, וקיים הופכי משמאל, כלומר איבר $latex {h}$ ש-$latex {hx=e}$.

 

בסימון מדויק יותר, החבורה היא זוג של קבוצה ופעולה. זוג כזה מסמנים ב-$latex {(G,\cdot)}$, או $latex {(G,+)}$, בהתאם לסימן שמציין את הפעולה.

מספר האיברים בחבורה נקרא ה"סדר" (או הגודל) של החבורה.

קיום ההופכי היא תכונה מועילה מאוד של פעולות: זהו כמו כפתור ה-$latex {backspace}$ במקלדת.

למה 2.2 ההופכי מימין שווה להופכי משמאל.

הוכחה: יהיה $latex {g}$ הופכי מימין של $latex {x}$, ו-$latex {h}$ הופכי משמאל. נתבונן בביטוי $latex {hxg}$. בגלל האסוציאטיביות אפשר לכתוב אותו כך, בלי סוגריים, ולשים את הסוגריים איך שרוצים. בדרך אחת לשים סוגריים מקבלים $latex {(hx)g=eg=g}$, ובדרך השנייה מקבלים $latex {h(xg)=he=h}$. אם כן, $latex {g=h}$.

הגדרה 2.3 החבורה $latex {G}$ נקראת קומוטטיבית, או אבלית (על שמו של $latex {Niels~~Henrik~~ Abel}$, מתמטיקאי נורווגי שכבר הוזכר לעיל, וחי בין השנים $latex {1802}$ ו-$latex {1829}$) אם הפעולה קומוטטיבית, כלומר $latex {ab=ba}$ לכל שני איברים $latex {a}$ ו-$latex {b}$ בחבורה.

 

מוסכמה: אם מסמנים את פעולת החבורה ב-$latex {+}$, הכוונה היא שהחבורה קומוטטיבית. ההפך אינו נכון: לפעמים מסמנים את הפעולה ככפל גם בחבורות קומוטטיביות.

אם סימן הפעולה הוא כפל, מסמנים את ההופכי של איבר $latex {a }$ ב-$latex {a^{-1}}$, ואם הסימן הוא חיבור מסמנים את ההופכי ב-$latex {-a}$.

כמה דוגמאות לחבורות קומוטטיביות:

1. $latex {(\mathbb{Z},+)}$, כלומר המספרים השלמים עם פעולת החיבור (הסימון $latex {\mathbb{Z}}$ בא מ-$latex {Zahle}$, שפירושו בגרמנית "מספר"). האיבר האדיש הוא כמובן $latex {0}$.
2. $latex {(\mathbb{Q},+)}$ - הרציונליים עם פעולת החיבור. $latex {\mathbb{Q}}$ בא מ-"$latex {quotient}$", שפירושו "מנה" - מספר רציונלי הוא מנה של שני מספרים שלמים.
3. $latex {~(\mathbb{R},+)}$ ( "$latex {Reals}$" פירושו "ממשיים").
4. $latex {~(\mathbb{C},+)}$ ($latex {"Complex"}$), המרוכבים עם פעולת החיבור.
5. ~את קבוצת הרציונליים שמרחיקים ממנה את $latex {0}$ מסמנים ב-$latex {\mathbb{Q}^*}$. הזוג $latex {(\mathbb{Q}^*,\times)}$, כלומר הרציונליים בלי ה-$latex {0}$ עם פעולת הכפל, היא חבורה. בדומה, $latex {,~(\mathbb{R}^*,\times),(\mathbb{C}^*,\times)}$ (הממשיים בלי $latex {0}$ והמרוכבים בלי $latex {0}$, עם פעולת הכפל) הן חבורות.
6. חבורת המספרים המרוכבים בעלי ערך מוחלט $latex {1}$ עם כפל.
7. $latex {\mathbb{R}^n}$ עם פעולת החיבור.
8. קבוצת המטריצות הלא סינגולריות מסדר $latex {n \times n}$ עם פעולת הכפל.החבורה האחרונה היא הדוגמה הראשונה שלנו לחבורה לא אבלית. כפל מטריצות, כידוע, אינו קומוטטיבי.

תרגיל: האם הקבוצה $latex {G=\left\{ x\in\mathbb{Q}|x>0\right\} }$ מהווה חבורה ביחס לפעולה $latex {a*b=\frac{ab}{2}}$?

פתרון:

1. סגירות: אם $latex {a,b\in\mathbb{Q}}$ אז $latex {a*b=\frac{ab}{2}\in\mathbb{Q}}$ וגם כיוון ש- $latex {\frac{ab}{2}>0}$ לכן $latex {a*b\in G}$.
2. אסוציאטיביות:

   $latex \displaystyle \left(a*b\right)*c=\left(\frac{ab}{2}\right)*c=\frac{\frac{ab}{2}c}{2}=\frac{a\frac{bc}{2}}{2}=a*\left(\frac{bc}{2}\right)a*\left(b*c\right) $

3. איבר יחידה: יהי $latex {a\in G}$, מחפשים $latex {e\in G}$ כך ש- $latex {a*e=a}$

   $latex \displaystyle a*e=\frac{ae}{2}=a\Rightarrow\frac{e}{2}=1\Rightarrow e=2 $

   ניתן לצמצם כיוון שידוע ש-$latex {a\neq0}$ ומספיק לבדוק רק כיוון אחד כי הפעולה היא קומוטטיבית.</li>

4. איבר הפכי: לכל $latex {a\in G}$ מחפשים $latex {b\in G}$ כך ש- $latex {a*b=2}$, כלומר $latex {\frac{ab}{2}=2}$, כלומר $latex {b=\frac{4}{a}\in G}$.
</ol>

לכן $latex {G}$ חבורה.

תרגיל:

נגדיר $latex {G=\left\{ z\in\mathbb{C}|\left|z\right|=1\right\} }$ עם פעולת הכפל ב-$latex {\mathbb{C}}$. האם $latex {G}$ חבורה?

אם כן, האם היא אבלית?

פתרון:

$latex {G}$ מייצגת בעצם את כל הנקודות על מעגל היחידה. כל מספר מרוכב על מעגל היחידה הוא מהצורה $latex {z=cis\alpha}$.

1. יהיו $latex {z=cis\alpha,w=cis\beta\in G}$, אז $latex {zw=cis\left(\alpha+\beta\right)\in G}$.
2. אסוציאטיביות נובעת מאסוציאטיביות ב- $latex {\mathbb{C}}$.
3. יחידה: $latex {1\in G}$ ולכל $latex {z\in G}$ מתקיים $latex {z\cdot1=z}$.
4. הופכי: לכל $latex {z\in G}$ מתקיים $latex {z^{-1}=\frac{1}{z}=\frac{\bar{z}}{\left|z\right|}=\bar{z}}$

$latex {\mathbb{C}}$ שדה כלומר מתקיים קומוטטיביות ולכן $latex {G}$ אבלית.

</blockquote>

2.1. $latex {(\mathbb{Z}_n,+)}$ - חבורת השאריות מודולו $latex {n}$, עם חיבור

חבורה חשובה במיוחד היא חבורת השאריות ממספר טבעי נתון.האדיש הוא כמובן $latex {0}$, וההופכי של $latex {a}$, כלומר $latex {-a}$, הוא $latex {n-a}$ אם $latex {a \neq 0}$, ו)כמובן( $latex {0}$ אם $latex {a=0}$. השאריות האפשריות בחלוקה ב-$latex {n}$ הן $latex {0,1, \ldots, n-1}$. לכן זוהי חבורה מסדר $latex {n}$.

3. חוק הצמצום

בחבורה יש חוק צמצום: אם $latex {ax=bx}$ אז $latex {a=b}$. כדי לראות זאת, קחו את השוויון $latex {ax=bx}$ וכפלו את שני האגפים מימין ב-$latex {x^{-1}}$. תקבלו: $latex {axx^{-1}=bxx^{-1}}$ כלומר $latex {ae=be}$ כלומר $latex {a=b}$.

באותה צורה מוכיחים שמותר גם לצמצם משמאל.

מכירים פעולות שאין בהן צמצום? בוודאי. כפל בממשיים: $latex {0 \times 2=0\times 3}$, ובכל זאת $latex {2 \neq 3}$. הסיבה היא כמובן של-$latex {0}$ אין הופכי לגבי הכפל.

תרגיל:

חשבו את לוח הכפל של חבורה מסדר $latex {3}$. כמה חבורות מסדר $latex {3}$ קיימות? האם כל חבורה מסדר $latex {3}$ היא אבלית?

פתרון:

$latex {G=\left\{ e,a,b\right\} }$. בלוח הכפל אסור שבשורה או בעמודה כלשהי יופיע אותו איבר פעמיים.

$latex {b}$	$latex {a}$	$latex {e}$
$latex {b}$	$latex {a}$	$latex {e}$	$latex {e}$
$latex {e}$	$latex {b}$	$latex {a}$	$latex {a}$
$latex {b}$	$latex {e}$	$latex {b}$	$latex {b}$

יש רק חבורה אחת כזו, עד כדי איזומורפיזם. כלומר - כל שתי חבורות מסדר $latex {3}$ הן איזומורפיות. נשים לב שבעצם $latex {b=a^{2}}$, כלומר $latex {G=\left\{ e,a,a^{2}\right\} }$. מאוחר יותר נראה שלכל מספר ראשוני $latex {p}$ יש רק חבורה אחת מסר $latex {p}$, והיא אבלית.

תרגיל:

חשבו את לוח הכפל של חבורה מסדר $latex {4}$. כמה חבורות מסדר $latex {4}$ קיימות? האם כל חבורה מסדר $latex {4}$ היא אבלית?

פתרון: נכתוב $latex {G=\left\{ e,a,b,c\right\} }$. נפריד לשני מקרים.

מקרה I: הריבוע כל כל איבר הוא $latex {e}$. כלומר $latex {a^{2}=e,b^{2}=e,c^{2}=e}$:

$latex {c}$	$latex {b}$	$latex {a}$	$latex {e}$
$latex {c}$	$latex {b}$	$latex {a}$	$latex {e}$	$latex {e}$
$latex {b}$	$latex {c}$	$latex {e}$	$latex {a}$	$latex {a}$
$latex {a}$	$latex {e}$	$latex {c}$	$latex {b}$	$latex {b}$
$latex {e}$	$latex {a}$	$latex {b}$	$latex {c}$	$latex {c}$

חבורה שמקיימת את התנאים הנ"ל נקראת חבורת קליין.

מקרה II:

קיים איבר לא אדיש שבחזקת שתיים לא שווה לאדיש. כלומר יש איבר שכפול עצמו הוא איבר שונה ממנו, שאינו אדיש. בה"כ נבחר $latex {a^{2}=b}$.

$latex {c}$	$latex {b}$	$latex {a}$	$latex {e}$
$latex {c}$	$latex {b}$	$latex {a}$	$latex {e}$	$latex {e}$
$latex {a}$	$latex {c}$	$latex {b}$	$latex {a}$	$latex {a}$
$latex {e}$	$latex {a}$	$latex {c}$	$latex {b}$	$latex {b}$
$latex {e}$	$latex {a}$	$latex {b}$	$latex {c}$	$latex {c}$

ניתן היה לבחור אופציות נוספות והיינו מקבלים טבלת כפל שקולה.

אלה כל האפשרויות. בכל המקרים הטבלה היא סימטרית ולכן החבורה היא אבלית.

החבורות לא איזומורפיות כי בחבורה הראשונה שנקראת חבורת קליין כל איבר בחזקת שתיים שווה לאדיש.

החבורה השנייה היא בעצם החבורה $latex {G=\left\{ e,a,a^{2},a^{3}\right\} }$ שהיא איזומורפית (מדוע?) לחבורה $latex {\mathbb{Z}_{4}}$.

אלו שתי החבורות היחידות מסדר $latex {4}$.

4. חזקות

כשמפעילים איבר $latex {a}$ על עצמו $latex {n}$ פעמים מסמנים את התוצאה ב-$latex {na}$ במקרה שסימן הפעולה הוא $latex {+}$, וב-$latex {a^n}$ אם סימן הפעולה הוא כפל. חוקי החזקות קיימים גם בחבורות. למשל, $latex {na+ma=(m+n)a,~~a^{n+m}=a^n\cdot a^m}$. כי אכן, חוק הפילוג של החיבור ושל החזקות הוא אותו חוק! זהו אותו כלל, בשני סימונים שונים. למדתם אותו בכיתה ג' או ד' בנוסח הראשון, ובתיכון בנוסח השני - בוודאי לא סיפרו לכם שזהו אותו חוק בדיוק!

עובדה שימושית היא שחזקות של אותו איבר מתחלפות. כלומר:

משפט 4.1 


$latex \displaystyle a^k \cdot a^\ell=a^\ell \cdot a^k$

הסיבה פשוטה - לפי האמור לעיל שני האגפים שווים ל-$latex {a^{k +\ell}}$.

תרגיל:

תהי $latex {G}$ חבורה עם פעולת כפל $latex {*}$. הוכיחו את הטענות הבאות:

א. אם $latex {\left(a*b\right)^{2}=a^{2}*b^{2}}$ לכל $latex {a,b\in G}$ אז $latex {G}$ אבלית.

פתרון:

צריך להוכיח שלכל $latex {a,b\in G}$ מתקיים $latex {ab=ba}$.

$latex \left(ab\right)\left(ab\right)=aabb=e$

$latex a^{-1}/\left(ab\right)\left(ab\right)=aabb/b^{-1}$

$latex a^{-1}ababb^{-1}=a^{-1}aabbb^{-1}$

$latex ba=ab$

לכן $latex {G}$ אבלית.

ב. הוכיחו כי אם $latex {a^{2}=e}$ לכל $latex {a\in G}$ אז $latex {G}$ אבלית.

פתרון א':

אם $latex {a^{2}=e}$ לכל $latex {a\in G}$ מתקיים $latex \displaystyle e=\left(ab\right)^{2}=a^{2}b^{2}=ee=e $

ולכן לפי הסעיף הקודם, \L{$latex {G}$} אבלית.

פתרון ב':

לכל $latex {a\in G}$ מתקיים $latex {a^{2}=e}$ ולכן

$latex aa=e$

$latex a=a^{-1} $

בפרט $latex {a^{-1}=a,b^{-1}=b,ba=\left(ba\right)^{-1}}$, לכן , $latex {ba=\left(ba\right)^{-1}=a^{-1}b^{-1}=ab}$, כלומר $latex {G}$ אבלית.

ג. הוכיחו כי $latex {G}$ אבלית אם ורק אם $latex {\left(a*b\right)^{n}=a^{n}*b^{n}}$ לכל $latex {n\geq1}$.

פתרון:

אם $latex {G}$ אבלית אז לכל $latex {a,b\in G}$ מתקיים $latex \displaystyle \left(ab\right)^{n}=\left(ab\right)\left(ab\right)\dots\left(ab\right)=\left(aa\dots a\right)\left(bb\dots b\right)=a^{n}b^{n} $

אם לכל $latex {a,b\in G}$ מתקיים $latex {\left(ab\right)^{n}=a^{n}b^{n}}$, אז בפרט עבור $latex {n=2}$ מתקיים $latex {\left(ab\right)^{2}=a^{2}b^{2}}$ ולכן לפי סעיף א', $latex {G}$ אבלית.

5. סדר של חבורה וסדר של איבר

כפי שכבר ציינו, מספר האיברים בחבורה $latex {G}$ נקרא סדר החבורה, והוא מסומן ב-$latex {|G|}$.

משפט 5.1 אם $latex {G}$ אבלית וסופית אז לכל איבר $latex {g}$ ב-$latex {G}$ מתקיים $latex {g^{|G|}=e}$.

הוכחה: נסמן $latex {|G|=n}$. יהיו $latex {u_1,u_2,\ldots, u_n}$ איברי החבורה. נתבונן בקבוצת מכפלות איברי החבורה ב-$latex {g}$, כלומר ב-$latex {\{gu_1,gu_2,\ldots,gu_n\}}$. לפי חוק הצמצום, כל האיברים האלה שונים, ולכן אלה כל איברי החבורה. ($latex {n}$ איברים שונים בקבוצה בת $latex {n}$ איברים הם הקבוצה כולה.) לכן מכפלתם היא מכפלת כל איברי החבורה, כלומר מכפלת כל האיברים האלה היא $latex {gu_1gu_2gu_3\ldots gu_n=u_1u_2,\ldots u_n}$. בגלל הקומוטטיביות $latex {gu_1gu_2gu_3\ldots gu_n=g^nu_1u_2,\ldots u_n}$,

וקיבלנו $latex {g^nu_1u_2,\ldots u_n=u_1u_2,\ldots u_n}$. צמצום נותן $latex {g^n=e}$.

מאוחר יותר נוכיח שהמשפט נכון גם לחבורות לא אבליות. בינתיים נוכיח משפט חלש יותר:

משפט 5.2

לכל איבר $latex {g}$ בחבורה $latex {G}$ יש חזקה $latex {k>0}$ ש-$latex {g^k=e}$.

הוכחה: נסמן $latex {|G|=n}$. נראה שקיים $latex {k \le n}$ ש-$latex {g^k=e}$. נתבונן ב-$latex {n+1}$ האיברים $latex {e=g^0,g=g^1,g^2,g^3,\ldots, g^n}$. מכיוון שכולם איברים מתוך $latex {n}$ איברי החבורה, שניים מהם חייבים להיות שווים (אין מקום ל-$latex {n+1}$ איברים שונים!) כלומר קיימים $latex {m}$ ו-$latex {\ell}$ שונים ש-$latex {g^m=g^\ell}$. נניח בלי הגבלת הכלליות ש-$latex {\ell >m}$, נאמר $latex {\ell=m+k~~(m>0)}$. אז $latex {g^m=g^{m+k}=g^mg^k}$. צמצום ב-$latex {g^m}$ נותן $latex {g^k=e}$.

תרגיל:

הוכיחו שלכל חבורה $latex {G}$ מסדר זוגי, קיים איבר $latex {e\neq a\in G}$ כך ש-$latex {a^{2}=e}$.

פתרון:

$latex {a^{2}=e}$ אם ורק אם $latex {a^{-1}=a}$ לכל $latex {a\neq e}$.

אם לא קיים איבר כנ"ל אז ניתן לחלק את כל אברי $latex {G}$ השונים מ-$latex {e}$ לזוגות, כלומר

$latex \displaystyle G=\left\{ e,a_{1},a_{1}^{-1},a_{2},a_{2}^{-1},\dots,a_{n},a_{n}^{-1}\right\} $

אבל אז ב-$latex {G}$ יש מספר אי זוגי של איברים בסתירה לנתון. לכן קיים איבר $latex {a}$ כך ש-$latex {a^{-1}=a}$, כלומר $latex {a^{2}=e}$.

הגדרה 5.3המספר המינימלי $latex {k}$ ש-$latex {g^k=e}$ נקרא הסדר של $latex {g}$ ומסומן ב-$latex {o(g)}$.

תרגיל:

חשבו את הסדר של האיבר הנתון בחבורה הנתונה.

א.$latex {6}$ ב- $latex {\mathbb{Z}_{21}}$ עם חיבור.

פתרון:

מחפשים מספר הכי קטן שאם כופלים אותו ב-$latex {6}$ מקבלים כפולה של $latex {21}$.

$latex {21}$ אינו כפולה של $latex {6}$. לעומת זאת, $latex {6\cdot7=42\equiv0\left(mod\;21\right)}$ ולכן $latex {o\left(6\right)=7}$.

ב.$latex {5}$ בחבורה הכפלית $latex {\mathbb{Z}_{7}^{*}}$.

פתרון:

$latex \displaystyle 5^{2}=25\equiv4,5^{3}\equiv5\cdot4\equiv6,5^{4}\equiv5\cdot6\equiv2,5^{5}\equiv5\cdot2\equiv3,5^{6}\equiv5\cdot3\equiv1 $

לכן $latex {o\left(5\right)=6}$.

ג.$latex {A=\left(\begin{array}{ccc} i & 0 & 0\\ 0 & -1 & 0\\ 0 & 0 & -i \end{array}\right)}$} ב-\L{$latex {GL_{3}(\mathbb{C})}$ - חבורת המטריצות ההפיכות מסדר $latex {3 \times 3}$ עם איברים ב-$latex {\mathbb{C}}$.

פתרון:

אם מעלים בחזקת $latex {n}$ מטריצה אלכסונית אז מקבלים מטריצה אלכסונית שאיבריה הם איברי המטריצה המקורית בחזקת $latex {n}$.

כלומר מחפשים $latex {k}$ מינימלי כך ש- $latex {\left(-i\right)^{k}=\left(-1\right)^{k}=i^{k}=1}$ ולכן $latex {k=4}$ לכן $latex {o\left(A\right)=4}$.

ד.$latex {1+i}$ בחבורה הכפלית $latex {\mathbb{C}^{*}}$.

פתרון:

נעבור לייצוג טריגונומטרי: $latex {1+i=\sqrt{2}cis\left(45\right)}$ מחפשים $latex {k}$ כך ש- $latex {\left(1+i\right)^{k}=1}$,

$latex \displaystyle 1=\left(\sqrt{2}cis\left(45\right)\right)^{k}=\left(\sqrt{2}\right)^{k}cis\left(45k\right) $

כלומר $latex {1=\left(\sqrt{2}\right)^{k}}$ ו-$latex {45k=360n}$ אבל לכל $latex {k}$ מתקיים ש- $latex {\left(\sqrt{2}\right)^{k}\neq1}$ לכן $latex {o\left(1\right)=\infty}$.

ה. $latex {\frac{1+i}{\sqrt{2}}}$ בחבורה הכפלית $latex {\mathbb{C}^{*}}$.

פתרון:

נעבור לייצוג טריגונומטרי: $latex {\frac{1+i}{2}=1cis\left(45\right)}$ מחפשים $latex {k}$ כך ש-$latex {\left(\frac{1+i}{\sqrt{2}}\right)^{k}=1}$,

$latex \displaystyle cis\left(0\right)=1=\left(cis\left(45\right)\right)^{k}=cis\left(45k\right) $

$latex {45k=360}$ כלומר $latex {k=8}$.

בהמשך נוכיח:

משפט 5.4 (משפט לגרנז') $latex {o(g)\mid |G|}$ (כלומר סדר של איבר מחלק את סדר החבורה).

---

שלשות פיתגוריות, מספרים מרוכבים וחבורות אבליות

אמנון יקותיאלי

אמנון יקותיאלי
המחלקה למתמטיקה
אוניברסיטת בן גוריון
amyekut@math.bgu.ac.il
03/04/2015

1. שלשות פיתגוריות

שלשה פיתגורית היא שלשה סדורה $latex {(a,b,c)}$ של מספרים שלמים חיוביים, אשר מקיימים את המשוואה

(1)

$latex \displaystyle .\ a^2 + b^2 = c^2 $

הסיבה לשם זה היא כי לפי משפט פיתגורס, אלו אורכי הצלעות במשולש ישר זוית. ליתר דיוק, בהנתן משולש ישר זוית עם בסיס באורך $latex {a}$ ואנך באורך $latex {b}$, אורך היתר של המשולש הוא $latex {c}$.

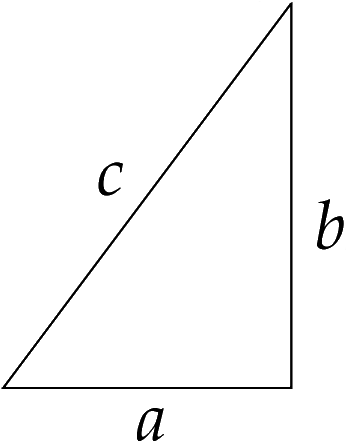
אומרים כי שתי שלשות פיתגוריות $latex {(a,b,c)}$ ו- $latex {(a',b',c')}$ הן שקולות אם המשולשים המתאימים דומים. זה אומר שיש מספר חיובי $latex {r}$ כך ש-

(2)

$latex \displaystyle (a', b', c') = (ra, rb, rc) $

(מתיחת המשולש הראשון פי $latex {r}$),או

$latex \displaystyle (a', b', c') = (rb, ra, rc) $

(מתיחה, והחלפה בין הבסיס והאנך). קל לראות כי המספר $latex {r}$ חייב להיות רציונלי.

שלשה פיתגורית $latex {(a,b,c)}$ נקראת מצומצמת אם המחלק המשותף המירבי של שלושת המספרים הוא $latex {1}$. השלשה הזאת נקראת מסודרת אם $latex {a \leq b}$. קל לראות שכל שלשה פיתגורית $latex {(a,b,c)}$ שקולה לשלשה מצומצמת ומסודרת יחידה $latex {(a',b',c')}$.

תרגיל 1. תהי $latex {(a,b,c)}$ שלשה פיתגורית מצומצת ומסודרת. אז $latex {a < b}$, וכן $latex {c}$ הוא איזוגי.

הנה שאלה מעניינת:

שאלה 1. האם יש אינסוף שלשות פיתגוריות מצומצמות ומסודרות?

התשובה היא כן. דבר זה כבר היה ידוע ליוונים הקדמונים. ישנה נוסחה (המיוחסת לאויקלידס) להצגת כל השלשות הפיתגוריות, והיא מראה שיש אינסוף שלשות פיתגוריות מצומצמות ומסודרות. אולם הנוסחה הזאת מסורבלת למדי, ולכן לא נרשום אותה כאן. מי שמעוניין יכול למצוא את הנוסחה הזאת בקלות בחיפוש באינטרנט. לדוגמה:

http://en.wikipedia.org/wiki/Pythagorean_triple

http://mathworld.wolfram.com/PythagoreanTriple.html

בהמשך נראה טיעון גיאומטרי יפה, אשר בעצם מתבסס על אותו רעיון כמו הנוסחה הישנה הזאת.

עבור מספר שלם חיובי $latex {c}$, נסמן ב- $latex {PT}(c) $ את קבוצת השלשות הפיתגוריות המצומצמות המסודרות בעלות יתר $latex {c}$. ניסוח אחר של שאלה 1 הוא: האם ישנם אינסוף מספרים שלמים חיוביים $latex {c}$ כך שהקבוצה $latex {PT}(c) $ איננה ריקה? למשל, תרגיל 1 מראה לנו שהקבוצה $latex {PT}(c) $ היא ריקה אם $latex {c}$ הוא זוגי.

שאלה יותר מעניינת היא:

שאלה 2. בהנתן מספר שלם חיובי $latex {c}$, מהו גודל הקבוצה $latex {PT}(c) $?

במאה ה- 19 נמצאה נוסחה פשוטה למדי לחישוב הגודל של $latex {PT}(c)$. אבל ההוכחה המקובלת עקיפה ומסובכת למדי.

שאלה עוד יותר מעניינת היא:

שאלה 3. בהנתן מספר שלם חיובי $latex {c}$, האם יש דרך אפקטיבית לחשב את אברי הקבוצה $latex {PT}(c) $, כלומר למצוא את כל השלשות המצומצמות המסודרות $latex {(a,b,c)}$ עם יתר $latex {c}$?

לפני שנים אחדות מצאתי דרך (אולי חדשה - קשה לעקוב אחרי הספרות בנושא הוותיק הזה) אשר עונה בחיוב על כל שלוש השאלות. מטרת המאמר הזה היא להסביר חלק מן הדרך הזאת. פרטים נוספים (כולל תשובות לשאלות 2 ו-3) ניתן למצוא בגירסה הארוכה של המאמר - ראו הקישור בסוף.

2. מספרים מרוכבים

עובדה שהיתה ידועה מזמן, היא כי ניתן להצפין שלשות פיתגוריות כמספרים מרוכבים בעלי ערך מוחלט $latex {1}$. נתחיל משלשה פיתגורית מצומצמת $latex {(a,b,c)}$. נעבור למספר המרוכב

$latex \displaystyle z := a + b \cdot \boldsymbol{i} $

אשר הערך המוחלט שלו הוא $latex {\lvert z \rvert = c}$. נתבונן במספר המרוכב

(3)

$latex \displaystyle .\ \zeta = r + s \cdot \boldsymbol{i} := \frac{z}{\lvert z \rvert} = \frac{a}{c} + \frac{b}{c} \cdot \boldsymbol{i} $

זהו מספר מרוכב על מעגל היחידה ברביע הראשון, שונה מ- $latex {1}$ ומ- $latex {\boldsymbol{i}}$, עם קואורדינטות רציונליות $latex {r = \frac{a}{c}}$ ו- $latex {s = \frac{b}{c}}$. יתר על כן, אנו רואים כי השלשה $latex {(a,b,c)}$ הינה מסודרת אם"ם המספר המרוכב $latex {\zeta}$ נמצא בשמינית השניה של מעגל היחידה. ראה ציור 1.

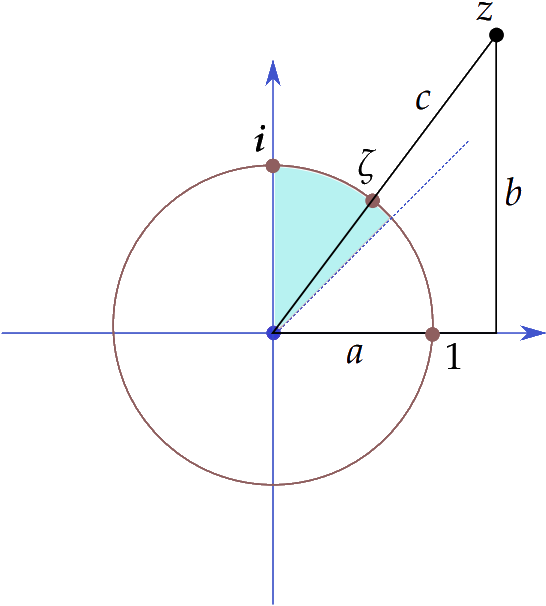
ציור 1

אפשר לשחזר את המספר המרוכב $latex {z}$, ולכן גם את השלשה הפיתגורית $latex {(a,b,c)}$, בקלות מתוך המספר המרוכב $latex {\zeta}$. עושים זאת ע"י סילוק המכנים מזוג המספרים הרציונליים $latex {(r,s) = (\frac{a}{c}, \frac{b}{c})}$.

בהנתן מספר מרוכב $latex {\zeta}$ עם קואורדינטות ממשיות במעגל היחידה, השונה מארבע הנקודות המיוחדות $latex {\pm 1, \pm \boldsymbol{i}}$, נסמן ב- $latex {\operatorname{pt}(\zeta)}$ את השלשה הפיתגורית המצומצמת המסודרת היחידה $latex {(a,b,c)}$ אשר מתאימה למספר $latex {\zeta}$, כלומר שעבורה מתקיימת נוסחה (3).

קיבלנו פונקציה $latex {\operatorname{pt}}$ מקבוצת המספרים המרוכבים עם רכיבים רציונליים על מעגל היחידה (ללא ארבע הנקודות המיוחדות) אל קבוצת השלשות הפיתגוריות המצומצמות המסודרות. הפונקציה הזאת היא סורז'קטיבית (כלומר התמונה היא כל הקבוצה). כל שלשה פיתגורית מצומצמת מסודרת מתקבלת בדיוק $latex {8}$ פעמים כ- $latex {\operatorname{pt}(\zeta)}$, מאחר שבדיוק אחד מבין שמונה המספרים

$latex \displaystyle \pm \zeta,\ \pm \boldsymbol{i} \cdot \zeta,\ \pm \bar{\zeta},\ \pm \boldsymbol{i} \cdot \bar{\zeta} $

נופל בשמינית השניה של מעגל היחידה. כמובן פרט למקרים המיוחדים $latex {\zeta = \pm 1, \pm \boldsymbol{i}}$. ראה ציור 2.

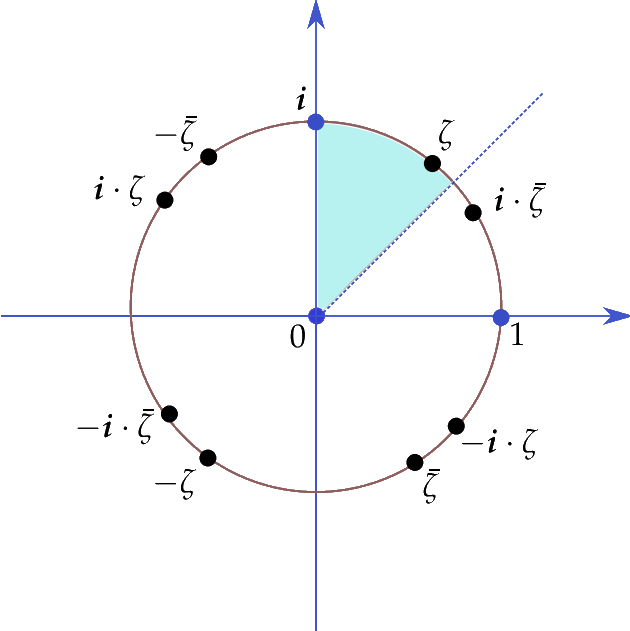
ציור 2

מסקנה: כדי להראות שיש אינסוף שלשות פיתגוריות מצומצמות מסודרות, מספיק להראות שיש אינסוף מספרים מרוכבים עם קואורדינטות רציונליות על מעגל היחידה.

כעת אפשר להציג את ההוכחה הגיאומטרית לעובדה הישנה (הידועה עוד מימי היוונים העתיקים) לכך שיש אינסוף שלשות פיתגוריות מצומצמות מסודרות. כלומר, תשובה חיובית לשאלה 1. נסמן ב- $latex {S}^1$ את מעגל היחידה (הספרה החד-מימדית). נתבונן בהטלה הסטריאוגראפית מהמעגל לישר הממשי, עם מוקד בנקודה $latex {\boldsymbol{i}}$ (הקוטב הצפוני), כפי שמתואר בציור 3. זו הפונקציה הביז'קטיבית (חד-חד ערכית ועל)

$latex \displaystyle f : {S}^1 - \{ \boldsymbol{i} \} \rightarrow \mathbb{R} $

השולחת את המספר המרוכב $latex {\zeta}$ למספר הממשי $latex {f(\zeta)}$, הנמצא על הקו הישר המחבר את $latex {\boldsymbol{i}}$ ו- $latex {\zeta}$. ראו ציור 3.

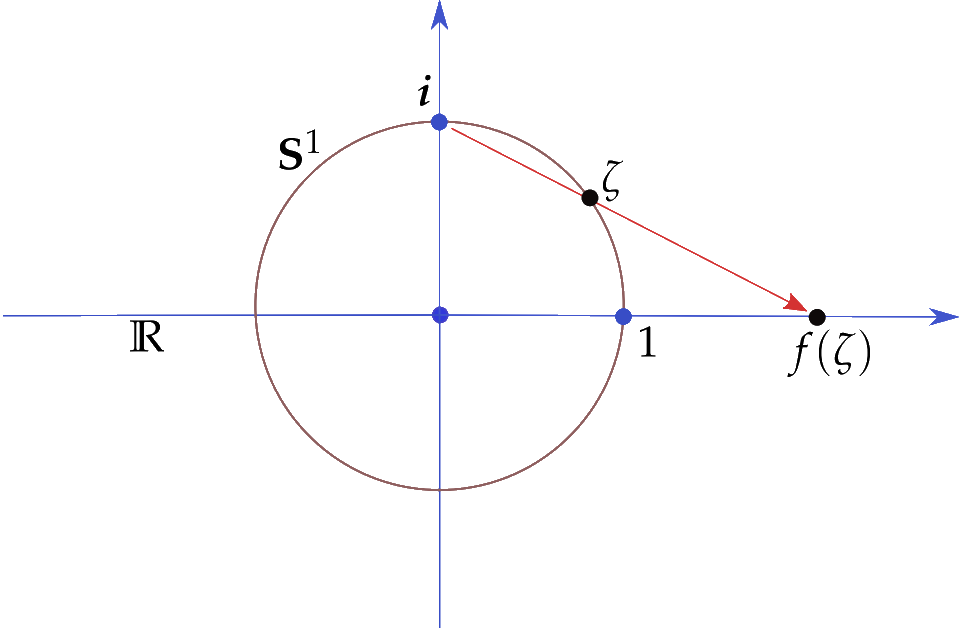
ציור 3

תרגיל 2. להראות כי למספר המרוכב $latex {\zeta}$ על מעגל היחידה יש קואורדינטות רציונליות אם"ם המספר הממשי $latex {f(\zeta)}$ הוא רציונלי. (רמז: משולשים דומים.)

מאחר שיש אינסוף מספרים רציונליים, אנו רואים שישנן אינסוף נקודות רציונליות על מעגל היחידה.

3. החבורה הכפלית של מעגל היחידה

קודם השתמשנו בסימון $latex {S}^1 $ עבור מעגל היחידה. כעת נעבור לסימון אחר לאותה קבוצה, המקובל בגיאומטריה אלגברית, והוא יהיה מועיל יותר עבורנו. מעתה נרשום

$latex \displaystyle . \ G(\mathbb{R}) := {S}^1 = \{ \zeta \in \ \mathbb{C} \mid \, \lvert \zeta \rvert  = 1 \, \} $

הקבוצה $latex {G(\mathbb{R})}$ הינה חבורה אבלית תחת פעולת הכפל, משום ש-

$latex \displaystyle \lvert \zeta_1 \cdot \zeta_2 \rvert = \lvert \zeta_1 \rvert \cdot  \lvert \zeta_2 \rvert  $

ו-

$latex \displaystyle . \ \lvert \zeta^{-1} \rvert  = \lvert \zeta \rvert  $

תהי $latex {G(\mathbb{Q})}$ קבוצת האיברים ב- $latex {G(\mathbb{R})}$ עם קואורדינטות רציונליות, כלומר

(4)

$latex \displaystyle . \ G(\mathbb{Q}) := \{ \zeta = s + r \cdot \boldsymbol{i} \, \mid \, s, r \in \mathbb{Q}, \, s^2 + r^2 = 1 \} \subset G(\mathbb{R}) \subset \mathbb{C} $

זוהי תת-חבורה, כי

$latex \displaystyle \begin{aligned} \zeta_1 \cdot \zeta_2 & = (r_1 + s_1 \cdot \boldsymbol{i}) \cdot (r_2 + s_2 \cdot \boldsymbol{i}) \\ & = (r_1 \cdot r_2 - s_1 \cdot s_2) + (r_1 \cdot s_2 + s_1 \cdot r_2) \cdot \boldsymbol{i} \end{aligned} $

ו-

$latex \displaystyle . \ \zeta^{-1} = s - r \cdot \boldsymbol{i} $

כדי לענות בחיוב על שאלה 1 (בדרך אחרת מזו שתוארה קודם לכן), אנחנו נראה כי החבורה האבלית $latex {G(\mathbb{Q})}$ היא אינסופית.

תחילה נמצא את האיברים מסדר סופי בחבורה $latex {G(\mathbb{Q})}$. אלו הם שורשי היחידה: האיברים $latex {\zeta \in G(\mathbb{Q})}$ המקיימים $latex {\zeta^n = 1}$ לאיזה $latex {n}$ שלם חיובי. ידוע (מתורת המספרים האלגברית) כי יש בדיוק ארבעה כאלה:

(5)

$latex \displaystyle .\ 1, \boldsymbol{i}, -1, -\boldsymbol{i} $

לכן, אם ניקח איזשהו איבר $latex {\zeta}$ בחבורה $latex {G(\mathbb{Q})}$ השונה מארבעת המספרים האלו, הרי תת-החבורה הציקלית

$latex \displaystyle \{ \zeta^n \mid n \in \mathbb{Z} \} \subset G(\mathbb{Q}) $

$latex {\operatorname{pt}(\zeta^n) = (a_n ,b_n ,c_n)}$	$latex {\zeta^n}$	$latex {n}$
$latex {(3,4,5)}$	$latex {\frac{3}{5} + \frac{4}{5} \boldsymbol{i}}$	1
$latex {(7, 24, 25)}$	$latex {-\frac{7}{25} + \frac{24}{25} \boldsymbol{i}}$	2
$latex {(44, 117, 125)}$	$latex {-\frac{117}{125} + \frac{44}{125} \boldsymbol{i}}$	3
$latex {(336, 527, 625)}$	$latex {-\frac{527}{625} - \frac{336}{625} \boldsymbol{i}}$	4

 טבלה 1

תהיה אינסופית. הבה נראה שיש איברים כאלה.

ניקח את השלשה הפיתגורית המוכרת $latex {(3,4,5)}$. האיבר המתאים ב- $latex {G(\mathbb{Q})}$ הינו

(6)

$latex \displaystyle .\ \zeta := \frac{3}{5} + \frac{4}{5} \cdot \boldsymbol{i} $

מאחר ש- $latex {\zeta}$ איננו אחד המספרים ב-(5), הרי זהו איבר מסדר אינסופי!

בטבלה 1 רשמנו את החזקות החיוביות הראשונות של המספר $latex {\zeta}$ מנוסחה (6), ואת השלשות הפיתגוריות המצומצמות המסודרות המתאימות.

הערה: את החומר הדרוש מתורת המספרים האלגברית אפשר למצוא בספר  Algebra, by M. Artin, Prentice-Hall.

תרגיל 3. מצא שלשה פיתגורית מצומצמת מסודרת עם יתר $latex {c = 3125}$. (רמז: להמשיך את טבלה 1.)

תרגיל 4.  מצא שלשות פיתגוריות מצומצמות מסודרות עם יתרים $latex {169}$ ו- $latex {2197}$. (רמז: להתחיל מהשלשה $latex {(5, 12, 13)}$, למצוא את המספר המרוכב $latex {\zeta}$ המתאים, כמו בנוסחה (6), ואז להכין טבלה כדוגמת טבלה 1.)

תרגיל 5. מצא שלשה פיתגורית מצומצמת מסודרת עם יתר $latex {65}$. (רמז: $latex {65 = 5 \cdot 13}$, ו- $latex {G(\mathbb{Q})}$ היא חבורה.)

ניתן לתת תיאור מלא של החבורה $latex {G(\mathbb{Q})}$, וכך גם לקבל תאור מלא של כל השלשות הפיתגוריות המצומצמות המסודרות. אולם לשם כך יש לדעת אלגברה יותר מתקדמת. כל זה מופיע בגירסה הארוכה יותר של מאמר זה, בקישור:

http://www.math.bgu.ac.il/~amyekut/popular/pythagoras.pdf

---

חידות

דניאל לובזנס

דבר העורך:

בחודש האחרון אירעו מספר תקלות במשלוח הפתרונות. הבעיה נפתרה. בכל זאת בשל הספק אאשר קבלת כל משלוח של פתרונות על ידכם (לכל היותר תוך יומיים מהמשלוח). אם לא קבלתם אישור אנא שלחו דוא"ל ל netgar2014@gmail.com. אם מי מכם שלח פתרונות נכונים ושמו אינו מופיע בין הפותרים אנא שלחו שנית את פתרונותיכם.

    לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 26.5.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.

חידה 1 –משולשים מחלקים משולש?

נחלק משולש לשלשה משולשים בצורה הבאה:

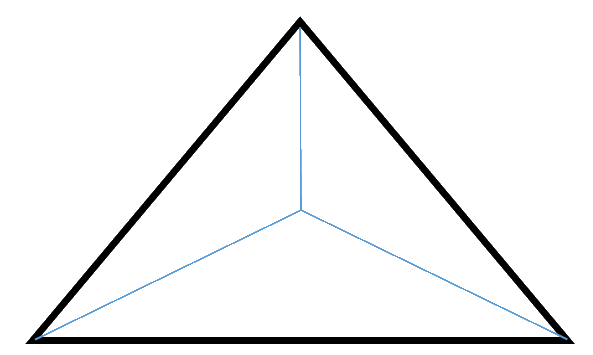
 כאן בכל קדקוד נפגשים $latex 3$ מקצועות.

איך נתן לחלק משולש ל $latex 19$ משולשים כך שבכל קדקוד יפגשו מספר זהה של מקצועות?

האם ניתן לחלק את המשולש ל $latex n>19$  משולשים כך שבכל קדקוד ייפגש מספר זהה של מקצועות?

חידה 2 –מספר בשתי שיטות ספירה?

האם ניתן למצוא מספר שהוא בן $latex 3$  ספרות כשהוא מוצג בשיטת $latex 7$  או בשיטת $latex 9$ . בשתי השיטות יש לו את אותן ספרות אלא בסדר הפוך.

חידה 3 –כמה נורות ידלקו?

נתונות $latex 1000$ נורות חשמליות, לצד כל אחת נמצא מפסק. כל לחיצה על המפסק משנה את מצב הנורה, אם הייתה כבויה היא נדלקת, ואם דלוקה היא נכבית.

במצב התחלי כל הנורות כבויות.

בשלב הראשון לוחצים בזה אחר זה על כל המפסקים.

בשלב השני לוחצים על כל מפסק שני (כלומר על המפסקים של הנורה השנייה, הרביעית, הששית, וכו').

בשלב השלישי לוחצים על כל מפסק שלישי.

וכן הלאה,

ולבסוף בשלב ה $latex 1000$ לוחצים על המפסק מספר $latex 1000$.

כמה נורות ידלקו בסופו של התהליך?

רמזים לחידות מגיליון אפריל 2015

חידה 1 – איך לחלק את הפאי? – נסו, באופן מחשבתי, לחלק את הפאי ע"י קוים נצבים בכיוון מסוים, אם לא הצלחתם סובבו את הקווים באפן רציף והסתכלו על החלוקה האפשרית.

חידה 2 – איך לחלק את העוגה? -  איך נתן לחלק עוגה ביחס $latex \frac{1}{3} - \frac{2}{3}$ בין $latex 2$ אנשים בצורה "צודקת"? באופן דומה לחלוקה לשני חלקים שווים? מכאן קל להמשיך….

חידה 3 – מסלול? – הראו שהמסלול הוא קו ישר, שהוא קוטר המעגל הגדול העובר דרך הנקודה $latex A$.

פתרון החידות גיליון מרס 2015

חידה 1 – עקומות על תפוחי אדמה -

ניקח את שני תפוחי האדמה ונקרבם זה לזה עד (שבאופן מחשבתי) המעטפת של האחד תחתוך את המעטפת של השני. החיתוך של שתי המעטפות הוא עקומה סגורה, שנמצאת על מעטפותיהם של שני תפוחי האדמה, כלומר עונה לדרישות החידה. יש לתת את הדעת שיש אין סוף עקומות כאלה!

חידה 2 – מה אורך החוט -

במרובע שאלכסוניו נצבים זה לזה סכומי ריבועי הצלעות המנוגדות זהים. משפט זה קל להוכיח, אחת ההוכחות מסתמכת על משפט דומה שהשתמשנו בו בחידת "קידוח הנפט" בגיליון ינואר של נטגר (ראה פתרון בגיליון מרס 2015). המעבר בין שני המשפטים מתואר סכמתית בתרשים הבא:

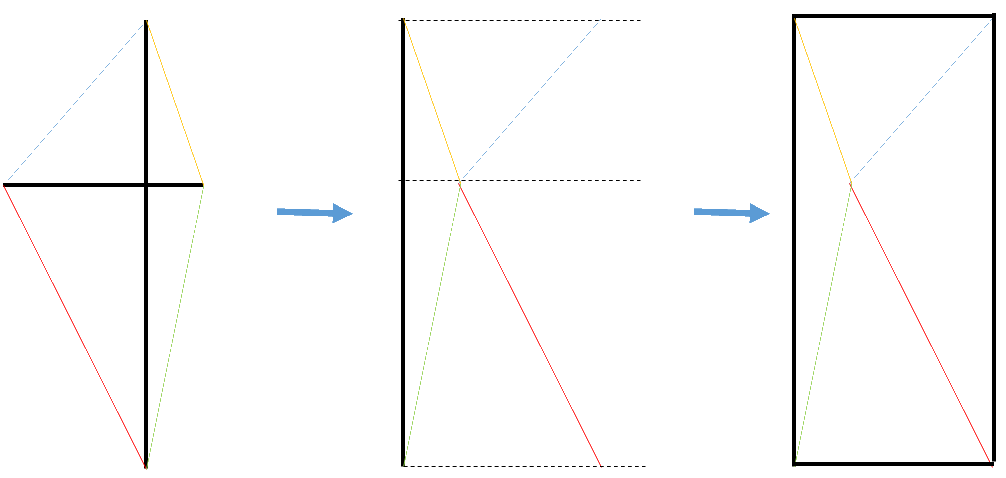
נרשום את המשוואות הבאות:

 $latex x+y = 30$

$latex x^2+13^2=y^2+7^2$

הראשונה נובעת מכך שאורך החוט השני $latex 30$ ס"מ, והשנייה מהמשפט על סכום ריבועי צלעות המרובע שאלכסוניו נצבים. הפתרון הוא:

$latex x=13$

$latex y=17$

חידה 3 – הזיקיות –

אם שתי זיקיות מצבעים $latex A$ ו$latex B$ נפגשות הן הופכות לזיקיות מצבע $latex C$. כלומר השינוי במספר הזיקיות מצבע $latex A$ ו $latex B$ הוא 1- ומצבע $latex C$ הוא $latex +2$. כשנסתכל במספרים מודולו $latex 3$ (כלומר השארית לאחר חלוקה ב$latex 3$), כל מספרי הזיקיות ישתנו ב $latex +2$. כלומר אם נסתכל במספרי הזיקיות מודולו $latex 3$ נראה שההפרשים בין מספריהן (מודולו $latex 3$) אינם משתנים! כדי שישארו זיקיות מצבע אחד בלבד מספר הזיקיות בצבעים האחרים יהיה $latex 0$ כלומר ההפרש בין מספריהן גם הוא $latex 0$!

במקרה שלנו מספרי הזיקיות מודולו $latex 3$ הם: $latex 2,1,0$ . אין זוג צבעים עם מספרי זיקיות זהים (מודולו $latex 3$) ולכן לא יתכן שישארו זיקיות בצבע אחד בלבד.

שמות הפותרים נכונה את החידות מגיליון אפריל 2015

בן בן דוד הולצר – חידה 3