נטגר גליון 16
דבר העורך
רון אהרוני
אלכסנדר גיבנטל, מתמטיקאי מאוניברסיטת ברגלי בקליפורניה, שמקצועו הוא גיאומטריה, תרם לגיליון הזה מאמר על המאפיינים הגיאומטריים של משטחים. במיוחד - קשר מפתיע, שהתגלה במאה התשע עשרה, בין קומבינטוריקה לעקמומיות של משטחים.
אנה ליזהטוב חוזרת עם מאמר על קומבינטוריקה אינסופית. בין השאר היא פותרת לנו חידה שהופיעה בגיליון קודם - מדוע השערת החלוקה הלא ידידותית של גרפים נכונה כשבגרף כל קדקוד מחובר רק למספר סופי של קדקודים אחרים.
כותב סדיר נוסף הוא אליהו לוי, שכתב מאמר בשבחן של השערות - כולנו אוהבים השערות, אבל מדי פעם צריך גם להסביר למה.
וכמובן - מדור החידות של דני לובזנס.
תודה לעושים (ולעושות) במלאכה.
האם כל טיפש יכול לשער השערות?
אליהו לוי
אם ה"אישה החוקית" בעולם המתמטיקה הם המשפטים והוכחותיהם, מהם לומד/ת המתמטיקאי/ת את ה"עובדות" - מה נכון ומה לא, הרי ה"פילגש" היא ההשערה - טענה שמתמטיקאי/ת בקי/אה ומנוסה החליט/ה שהיא "בוודאי נכונה", אחרי שבדק/ה מקרים פרטיים ושקל/ה נימוקים בכובד ראש, והוא/היא מכריז/ה על ההשערה, שבדרך כלל תיקרא על שמו/ה. אבל ללא הוכחה לכאן או לכאן יכולה ההשערה להיות באותה מידה נכונה כמו לא (ואולי אפילו יותר נורא מזה - לא ניתנת להכרעה כלל מהאקסיומות שלנו…), ובתולדות המתמטיקה קרו כל האפשרויות האלו.
וקל להבין (ולהצדיק) את אימרתו המפורסמת של פאול ארדש: "כל טיפש יכול להציע השערות", אבל זה לא בדיוק כך.
נזכיר כמה השערות בעלות "ערך פיננסי": בשנת 2000, עם המילניום, החליט מכון קליי $latex (Clay thinspace Mathematics thinspace Institute)$, מכון פרטי במדינת מסצ'וסטס, ארה"ב, שנוסד אז למען קידום המתמטיקה, להתחיל את פעילותו בהצעת שבעה פרסים, כל אחד בסך מיליון דולר, למי שיפתור שבע בעיות מתמטיות קשות מאוד, ביניהן הוכחת השערות אלו (ולפעמים גם עבור הוכחת אי-נכונותן).
על רבים מוסכם, שהבעיה הלא פתורה הראשונה במעלה במתמטיקה כיום היא הוכחת נכונותה (או הוכחת אי-נכונותה) של השערת רימן $latex (Riemann thinspace Hypothesis)$, וזו אחת מבעיות המילניום. היא מנוסחת כהשערה על הערכים בהם מתאפסת פונקציה שנקראת פונקצית זטה (האות היוונית $latex {zeta}$) של רימן, שהיא פונקציה מסויימת המוגדרת על מספרים מרוכבים ומקבלת ערכים מרוכבים.
נתאר את השערת רימן בלשונו של מרכוס דו סוטוי $latex (Marcus thinspace du thinspace Sautoy)$ בספרו "המוזיקה של המספרים הראשוניים": המספרים הראשוניים מופיעים בין סדרת המספרים הטבעיים באופן שנראה לא סדיר. עם זאת, הם מהווים סדרה המוגדרת באופן יחיד. אם נראה את הופעתם בין המספרים הטבעיים כמוסיקה, הרי הערכים בהם מתאפסת פונקצית זטה של רימן הם התוים, והשערת רימן אומרת שבתזמורת המנגנת מוסיקה זו, כל התוים מנוגנים באותה עוצמה. מטבע הדברים, השערה זו קשורה לאין-ספור טענות הקשורות למספרים הראשוניים ולהתפלגותם בין המספרים הטבעיים.
בעזרת מחשבים הראו שהשערת רימן נכונה עבור מילירדים של אפסים של פונקציית זטה. יש האומרים שזו "הוכחה ניסויית" לכך שהיא נכונה, וצריך להפסיק לדקדק דקדוקי עניות ולהגיד שהיא נכונה ודי. לזה אפשר לענות שעם כל הכבוד להוכחות ניסוייות כאלה, אם מישהו ימצא דוגמא נגדית, או באופן כלשהו יוכיח "ממש" שההשערה לא נכונה, תיקרוס ה"ההוכחה הניסויית" כמגדל קלפים. מתמטיקאים רגילים שלהוכיח משהו פירושו שהאפשרות שהוא לא נכון הוסרה מן הפרק.
ועוד: את הבדיקות במחשב, כמובן שעשו עם מספרים שאפשר לחשב בהם. אבל ההשערה מדברת על כל אינסוף השורשים של פונקציית זטה. ואפילו אם היינו יכולים לבדוק עד השורש ה-$latex {10^{1000}}$, עדיין בין $latex {10^{1000}}$ ואינסוף יש לאין ערוך יותר מספרים מאשר עד $latex {10^{1000}}$ - את הבדיקה ערכנו בקבוצה "מאוד לא מייצגת" של ה"זאטוטים" הקטנים מ-$latex {10^{1000}}$. הלא כן?
תורת המספרים, והמספרים הראשוניים בפרט, מצאו מאז שנות השבעים שימוש מפתיע בהצפנה, החל מהדרך בה מכשיר הכספומט יכול לוודא שהוקש מספר סודי נכון בלי שמי שמוצא את הכרטיס יוכל לחשב את המספר הסודי, ועד כל התקשורת הסודית באינטרנט, ועד אפילו שירותי ריגול. בעשרים השנים האחרונות נמצא להם מתחרה בדמות מושג מתמטי, עם דמיון מסויים להם אבל עוד יותר מתוחכם - עקומים אליפטיים סופיים. גם להם יש פונקצית זטה, ואחת מבעיות המילניום היא להכריע השערה לגביה, שנקראת השערת $latex Birch$ ו$latex Swinnerton-Dyer$. נושאים אלה הם מצד אחד מתמטיקה אזוטרית בעלת יופי מיוחד למי שמכיר אותה, ומצד שני האפשרות או אי האפשרות לפצח את הצפנים שהוזכרו עלולה להיות תלויה בהם.
מה שיכול לפצח חלק גדול מהתקשורת המוצפנת הוא אם ימצאו דרך מהירה לפרק מספר לגורמיו הראשוניים. כאן מדובר במספר "גדול" בעל מאות או אלפי ספרות. במלה "מהירה" מתכוונים לאופן התלות של זמן החישוב באורך הקלט $latex {ell}$. לגבי נתון מספרי אורך הקלט הוא מספר הספרות (אם רוצים, הבינריות). אם זמן החישוב הוא לא יותר מאורך הקלט בחזקה קבועה (נניח $latex {ell^3}$ אבל באופן תאורטי מרשים גם $latex {ell^{100}}$), אומרים שזמן החישוב פולינומיאלי וזה נחשב לחישוב קל ומהיר. למשל האלגוריתם של אוקלידס מוצא מחלק משותף מקסימלי בזמן פולינומיאלי (כמובן, בלי לפרק לגורמים ראשוניים!). את מחלקת הבעיות שאפשר לפתור בזמן פולינומיאלי מסמנים ב $latex {textrm{P}}$.
ברור שנוכל למצוא את הגורמים של $latex {n}$ ע"י בדיקת כל המספרים עד $latex {n}$, אבל זה ידרוש סדר גודל של $latex {nsim10^ell}$ פעולות, וזה מעריכי ולא פולינומיאלי. כיום ידועות שיטות לפירוק יותר מהירות ממעריכיות, אבל לא פולינומיאליות, ולכן "עדיין" הצפנים בטוחים. אבל דבר אחד אפשר להגיד: אם מישהו נתן לנו מועמדים לגורמים, דרוש רק זמן פולינומיאלי לבדוק אם אלה אכן גורמים. לבעיות כאלה, בהן בדיקת מועמד לפתרון היא "מהירה", קוראים $latex {textrm{NP}}$ מ$latex Nondeterministic thinspace Polynomial$ (פולינומיאלי, בתנאי שיש לנו מחשב לא דטרמיניסטי שבודק בבת אחת את כל האפשרויות$latex {ldots}$). בדומה לבעיית הפירוק לגורמים, אפשר לפתור בעייה $latex {textrm{NP}}$ ע"י בדיקת כל האפשרויות, אבל זה ידרוש בדרך כלל זמן מעריכי.
במיוחד, אם ננסח את האקסיומות והלוגיקה של ענף במתמטיקה באופן פורמלי לחלוטין, אזי בדיקה, האם מועמדת להוכחה היא אכן הוכחה, ניתנת לביצוע באופן אוטומטי והיא פולינומיאלית באורך הקלט (שבמקרה זה הוא מספר התוים). לכן הבעיה למצוא למשפט באורך $latex {ell}$ הוכחה מאורך לא יותר מ $latex {ell^{100}}$, אם יש כזו, היא $latex {textrm{NP}}$ (ואם ההוכחה הכי קצרה היא מאורך יותר מ $latex {ell^{100}}$ איש לא יוכל לכתוב אותה ולכן היא לא קיימת לגבינו). מבחינה זו, "המתמטיקה היא $latex {textrm{NP}}$".
ברור ש $latex {textrm{P}subsettextrm{NP}}$ (כלומר כל בעיה שהיא $latex {textrm{P}}$ היא $latex {textrm{NP}}$, מדוע?) אבל עד כמה שהדבר מוזר, לא ידוע אם $latex {textrm{NP}}$ לא שווה ל $latex {textrm{P}}$, כלומר האם אי אפשר לפתור את כל הבעיות ה $latex {textrm{NP}}$ באופן מהיר, למרות שרוב אנשי מדעי המחשב סבורים ש $latex {textrm{NP}netextrm{P}}$. השאלה האם $latex {textrm{NP}=textrm{P}}$ (או, מוטב לאמר, הכרעת ההשערה ש $latex {textrm{NP}netextrm{P}}$) היא אחת מבעיות המילניום.
יתר על כן, ע"י ניתוח מופשט מהו למעשה, באופן לוגי, מחשב, הראו רשימה ארוכה של בעיות $latex {textrm{NP}}$ שנקראות $latex NP-complete$ שכל אחת מהן יכולה לתפקד כמין מחשב עד כדי זמן חישוב פולינומיאלי, ולכן אם אפשר לפתור אחת מהן בזמן פולינומיאלי אזי $latex {textrm{NP}=textrm{P}}$ (ואז, אם נקבל את האמור לעיל על הוכחות פורמליות, "המתמטיקה היא טריוויאלית"$latex {ldots}$)
ביבליוגרפיה
J.Carlson, A.Jaffe and A.Wiles, ed. The Millennium Prize Problems. Clay Mathematics Institute and American Mathematical Society, 2006.
מרכוס דו סוטוי, המוזיקה של המספרים הראשוניים, מאנגלית: אוריאל גבעון, ידיעות ספרים, 6002.
גיאומטריה של משטחים ומשפט Gauss Bonnet
אלכסנדר ג'יבנטל תרגם: אליהו לוי
החוג למתמטיקה באוניברסיטת ברקלי
אלכסנדר ג'יבנטל Alexander Givental
גיאומטריה של משטחים ומשפט Gauss Bonnet
1. טופולוגיה מול גיאומטריה.
טופולוגיה היא גיאומטריה ללא מדידת מרחק. בעיני טופולוג פני כדור הארץ ופני כדור פינג-פונג הם זהים, ובן אדם דומה לבייגל עם שני חורים: אחד בנחיריים, והשני במערכת העיכול. במאמר הזה ננסה להבין תכונות טופולוגיות וגיאומטריות של משטחים.
למשטח יש מאפיינים טופולוגיים: האם הוא סגור, כמו פני כדור או טורוס (המעטפת של גלגל ים או בייגל), ואם כן - כמה חורים יש בו? בטופולוגיה אין חשיבות למרחקים. פני כדור גדול ופני כדור קטן הם זהים מבחינה טופולוגית, והמטעפת של בייגל שווה למעטפת של גלגל ים. יש למשטחים גם תכונות גיאומטריות, שבהן למרחק יש משמעות. פני כדור הארץ הם כל כך חסרי עקמומיות שנדמה לנו שהם מישור - ואכן כך האמינו עד לא כל כך מזמן. הנסיך הקטן, שחי על כוכב קטן, יודע שהכוכב שלו הוא כדורי, כי פני הכוכב שלו עקמומיים.



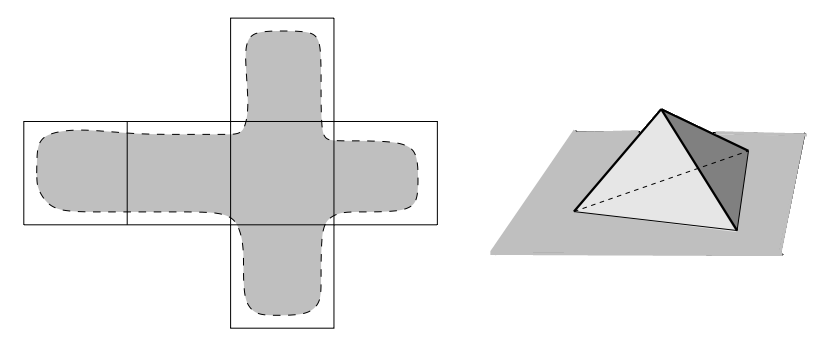
מישור גליל פני כדור מישור
אילו מבין המשטחים שבציור אפשר לעוות זה לזה (כלומר להפוך זה לזה בלי לחתוך ובלי להדביק) ואילו אי אפשר?
על אלה שאפשר אומרים שיש להם אותה טופולוגיה.
עשו חתכים בגליון נייר, והכינו משטח שיש לו אותה טופולוגיה כמו למסכה.
לגליון הנייר החתוך שתכינו ולמסכה עדיין תהיה גיאומטריה שונה. ובאמת, בגיאומטריה, הצורה והגודל המדוייקים חשובים. עיוות, למשל מתיחה, משנה צורות וגדלים.
2. מכופף או מעוקם?
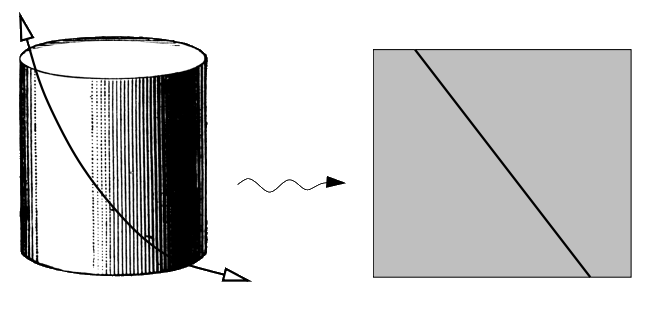
גליון נייר אפשר לכופף במרחב וכך לקבל צורה חדשה. הניסוי הבא מדגים את העובדה שכיפוף כזה לא משנה את הגיאומטריה הפנימית של המשטח (כלומר, את המרחקים והזוויות כפי שהיה מודד אותם יצור שחי במשטח ואינו יכול לעזוב אותו).
עיטפו גליל בגליון נייר, מיתחו שרוך נעל עליו כמו שרואים בציור, וסמנו את מסלולו במרקר. כעת שחררו את גליון הנייר - המסלול יהיה קו ישר.
קחו גוף קשיח בצורת חרוט ובצעו אותו ניסוי עליו. מה מצאתם?
נסו כעת לעטוף חצי-כדור ע"י גליון נייר - לא תצליחו! זאת כי הכדור הוא מעוקם.
העיקום הוא מה שמונע לעטוף משטח אחד על אחר בלי מתיחות וקמטים. זוהי תכונה גיאומטרית פנימית של משטח ואינה יכולה להיעלם כאשר מכופפים.
כיצד לכמת עיקום?
שאלה: האם שני פני-כדור בעלי רדיוסים שונים מעוקמים באופן שונה?
נסו (או דמיינו) שחותכים חתיכות משני כדורים מגומי בגודל שונה ועוטפים אחד על השני בלי חיתוכים וקימוטים.
3. השיטה. הציור הבא מתאר את הרעיון העיקרי. משטח חלק אפשר לקרב ע"י פיאון, כלומר משטח שעשוי ממצולעים שטוחים מחוברים בצלעותיהם או בקדקדיהם.

בקרו באתר http://www.vismath.de/vgp/content/surfaces והשתעשעו עם הSphere applet ותיראו איך פיאונים עם יותר ויותר צלעות (שנעשות יותר ויותר קטנות) נותנים קירוב יותר ויותר טוב למשטח וגורמים לו להיראות יותר ויותר חלק.
כל התכונות הגיאומטריות של משטחים צריכות להתגלות איכשהו ע"י התכונות הגיאומטריות של פיאונים.
4. העיקום שוכן בקדקדים. מכל פיאון, חיתכו חלק משטח פניו שלא מכיל קדקדים. אז תוכלו ליישר בו את הכיפוף לאורך הצלעות וכך לפתוח אותו לצורה שטוחה במישור.
בניגוד לכך, כמעט תמיד אפילו חלק קטן סביב קודקוד לא תוכלו לפתוח על השולחן (בלי לקפל).
5. הגירעון הזוויתי Angular Defect. כדי שכן יהיה אפשר לשטח אותה, הפינה המרחבית ליד קודקוד של פיאון צריכה לקיים: סכום הזוויות בפינה סביב הקודקוד הוא זוית מלאה, כלומר $latex {360^\circ}$.
להפרש: $latex {360^\circ}$ פחות סכום הזוויות סביב קודקוד קוראים: הגירעון הזוויתי בקודקוד זה.
הגירעון הזוויתי בקודקוד מבטא כמה עיקום שוכן בקודקוד זה.
 גירעון זוויתי אפס
גירעון זוויתי אפס
 גירעון זוויתי חיובי
גירעון זוויתי חיובי
גירעון זוויתי שלילי
שאלת ביקורת: כאשר הפינה בצורת ציפור בציור בצד שמאל למטה מנפנפת בכנפיה. האם הגירעון הזוויתי בקודקוד משתנה?
שאלה לחידוד המוח: לשקיות למתנות יש ארבע פינות למטה, אבל מוכרים אותן מקופלות שטוחות. בחנו שקית כזו והסבירו כיצד זה יכול להיות.
גירעונות זוויתיים כוללים.
מלאו את הטבלה
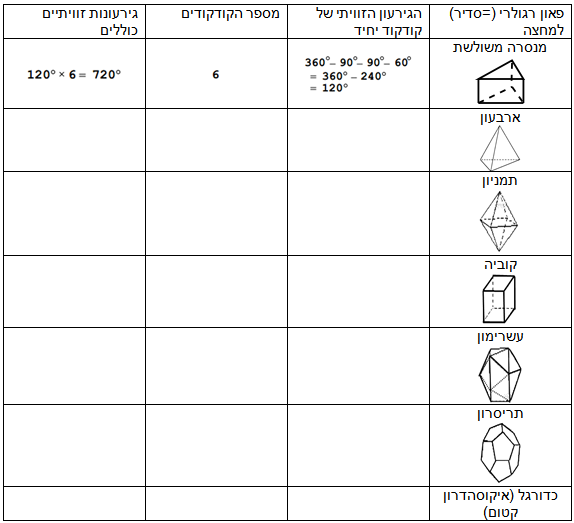
8. מדוע הגירעון הזוויתי הכולל - סכום הגרעונות הזוויתיים של כל הקודקודים בפיאון - ייצא תמיד אותו דבר?
נסמן ב $latex {V}$, $latex {E}$ ו $latex {F}$ את מספרי הקודקודים, המקצועות והפיאות של פיאון נתון. לפי ההגדרה,
הגירעון של קודקוד כלשהו = $latex {360^\circ}$ פחות סכום הזוויות סביב קודקוד זה.
אם נסכם, נקבל:
הגירעון הכולל של כל הקודקודים = $latex {360^\circ\times V}$ פחות סכום כל הזוויות בכל הקודקודים.
זיכרו שיוויון זה. כעת נשנה את נקודת הראות. סכום כל הזוויות בכל הקודקודים שווה לסכום כל הזוויות בכל הדפנות.
מהציור רואים ש
סכום הזוויות בדופן אחת =
$latex {180^\circ}$ $latex {\times}$ מספר הצלעות בדופן פחות $latex {360^\circ}$.
אם נסכם, נקבל
סכום כל הזוויות בכל הדפנות =
$latex {180^\circ}$ $latex {\times}$ המספר הכולל של כל הצלעות בכל הדפנות בפיאון פחות $latex {360^\circ\times F}$.
אם נביא בחשבון שכל מקצוע מופיע כצלע בדיוק בשתי דפנות, נוכל לבטא תוצאה זו בצורה:
סכום כל הזוויות בכל הקודקודים = $latex {360^\circ\times E - 360^\circ\times F}$.
כעת נצרף זאת עם מה שביקשנו לזכור
משפט. הגירעון הזוויתי הכולל = $latex {360^\circ\times(V-E+F)}$.
גיאומטריה מול קומבינטוריקה. נקרא לגירעון הזוויתי הכולל של פיאון $latex {P}$ מחולק ב $latex {360^\circ}$ בשם מספר גאוס של $latex {P}$, ול $latex {V-E+F}$ בשם מספר אוילר של $latex {P}$. מספר גאוס מאפיין את הגיאומטריה של $latex {P}$, בעוד שמספר אוילר מאפיין את הקומבינטוריקה של $latex {P}$. המשפט אומר שעבור כל פיאון $latex {P}$,
מספר גאוס של $latex {P}$ = מספר אוילר של $latex {P}$.
אם כך, הקומבינטוריה של פיאון מציבה הגבלות על הגיאומטריה שלו, וההפך, הגיאומטריה של פיאון מציבה הגבלות על הקומבינטוריקה שלו. קשר זה בין גיאומטריה וקובינטוריקה אמנם ראוי לציון אבל לא מפתיע. אבל כעת נסיק ממנו שאם נתונים שני פיאונים, $latex {P}$ ו $latex {T}$, אזי מספר גאוס של $latex {P}$ = מספר אוילר של $latex {T}$, אפילו אם על $latex {P}$ ו $latex {T}$ ידוע רק שיש להם אותה טופולוגיה.
לשם כך, נבנה שני פיאונים, $latex {P'}$ ו $latex {T'}$, שיש להם אותה קומבינטוריקה (אבל אולי גיאומטריה שונה) וכך של- $latex {P'}$ יש אותה גיאומטריה כמו $latex {P}$ (אבל אולי קומבינטוריה שונה) ול- $latex {T'}$ יש אותה גיאומטריה כמו $latex {T}$ (אבל אולי קומבינטוריה שונה).
הרעיון הוא פשוט מאוד. חלוקת פיאות של פיאון לפיאות יותר קטנות משנה את הקומבינטוריקה שלו, אבל לא משנה את הגיאומטריה. לכן מספר גאוס לא משתנה, ולפי המשפט מספר אוילר שלו גם הוא נשאר כשהיה.
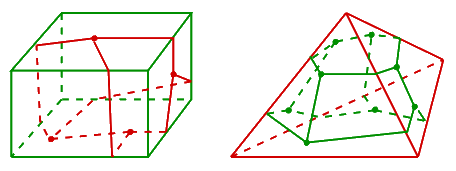
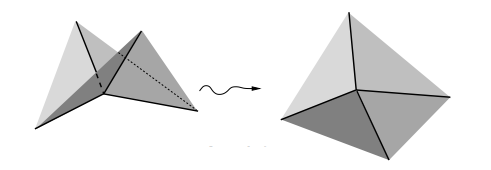
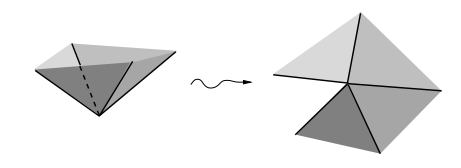
נדגים את הרעיון בדוגמה בציור בה $latex {P}$ הוא תיבה מלבנית, ו $latex {T}$ הוא ארבעון. מאחר של- $latex {P}$ ו $latex {T}$ יש אותה טופולוגיה, אנו יכולים לצייר תמונה של $latex {T}$ על פניו של $latex {P}$ (ראו בציור משמאל, בו סומנו בנקודות עבות קודקודים של $latex {T}$ על פניו של $latex {P}$). מקצועותיו של $latex {P}$ והקוים שמחברים את הנקודות העבות, יהיו מקצועות הפיאון שאנו קוראים לו $latex {P'}$. יש לו אותה גיאומטריה כמו $latex {P}$ ובמיוחד יש לו אותו גירעון זויתי כולל, מאחר שהקודקודים החדשים שיצרנו הם בעלי גירעון זוויתי אפס.
תרגיל:
בציור משמאל, מיצאו $latex {10}$ קודקודים של $latex {P'}$ שאינם של $latex {P}$ והראו שבכל אחד מהם יש גירעון זוויתי אפס.
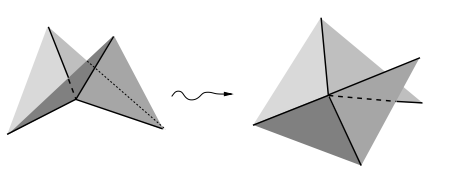
אם כעת "נלביש" את $latex {P}$ על $latex {T}$, נקבל את $latex {P}$ מצוייר על פניו של $latex {T}$ (הציור מימין). כמו קודם, כל הקווים מחלקים את דפנותיו של $latex {T}$ לדפנות של פיאון חדש, $latex {T'}$, שיש לו אותה קומבינטוריקה כמו $latex {P'}$ אבל אותו גירעון זוויתי כולל כמו $latex {T}$.
תרגיל:
מיצאו במישרין את המספרים $latex {V}$, $latex {E}$, $latex {F}$ עבור $latex {P'}$ (בציור משמאל) ו $latex {T'}$ (בציור מימין) ובידקו שהם מתלכדים.
ולבסוף (הצדיקו כל שוויון)
מספר אוילר של $latex {P}$ = מספר גאוס של $latex {P}$ =
מספר גאוס של $latex {P'}$ = מספר אוילר של $latex {P'}$ =
מספר אוילר של $latex {T'}$ = מספר גאוס של $latex {T'}$ =
מספר גאוס של $latex {T}$ = מספר אוילר של $latex {T}$.
בכך הוכחנו:
משפט גאוס בונה (Gauss-Bonnet) עבור פיאונים.
מספרי גאוס ואוילר של כל פיאון שווים זה לזה ותלויים רק בטופולוגיה של הפיאון.
מסקנה. אם לפיאון יש אותה טופולוגיה כמו לפני כדור, אזי מספר אוילר שלו הוא $latex {V-E+F=2}$ והסכום הכולל של הגרעונות הזוויתיים שלו הוא $latex {720^\circ}$.
שאלה לחידוד המוח: סכמו את כל הגירעונות של הפיאון בציור שיש לו אותה טופולוגיה כמו טורוס, והשוו עם מספר אוילר $latex {V-E+F}$.
תרגיל: מיצאו את מספרי גאוס ואוילר של כל פיאון שיש לו אותה טופולוגיה כמו פניה של ביגלה.
ביגלה $latex \qquad$ טורוס

10. העיקום של גאוס. אנו חוזרים כעת לגיאומטריה של משטחים חלקים. למשטחים כאלה אפשר להתקרב ע"י פיאונים בעלי הרבה פיאות קטנות והרבה קודקודים עם גירעונות זוויתיים קטנים מאוד (אבל בדרך כלל שונים מאפס). סכום הגירעונות הזוויתיים בקודקודים שנמצאים בתחום כלשהו במשטח מאפיין את העיקום באותו איזור. הוא נקרא העיקום של גאוס של התחום. אם הוא שונה מאפס, אזי את התחום הזה של המשטח, יהא קטן ככל שיהא, אי אפשר לשטוח על חלק ממישור או לעטוף בגליון נייר בלי מתיחות או קיפולים.
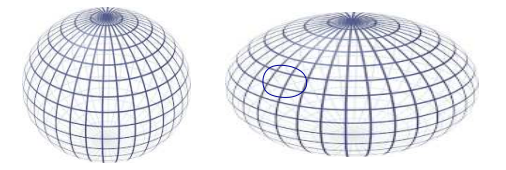
אם ניקח קירובים טובים יותר ויותר למשטח ע"י פיאונים, ועליהם נפעיל את משפט גאוס-בונה עבור פאונים, נקבל את התוצאה הבאה.
משפט גאוס-בונה עבור משטחים
העיקום של גאוס הכולל של משטח סגור תלוי רק בטופולוגיה של המשטח ושווה ל $latex {2\pi}$ כפול במספר אוילר של המשטח.
כתבנו כאן $latex {2\pi}$ (במקום $latex {360^\circ}$) כי גאוס מדד זווית מלאה לא כ $latex {360^\circ}$ אלא כיחס, השווה ל $latex {2\pi}$, בין ההיקף מסביב לקודקוד של זווית מלאה לבין רדיוס המעגל.
בעיה. הראו שלפני כדור יש עיקום של גאוס קבוע (כלומר בעל אותו ערך ליד כל הנקודות בפני הכדור) ומיצאו את ערכו של עיקום גאוס של כדור בעל רדיוס $latex {R}$.
הערות היסטוריות. משפט גאוס-בונה עבור פיאונים שיש להם אותו טופולוגיה כמו פני-כדור נתגלה למעשה ע"י רנה דקרט René Descartes (1596-1650).
(Carl Friedrich Gauss (1777-1855 הכניס את מושג העיקום, הוכיח שהוא אינו משתנה אם מכופפים את המשטח, והוכיח את מה שאנו מכנים משפט גאוס-בונה עבור משטחים. (Pierre Ossian Bonnet (1819-1892 מצא הכללה של משפט זה למקרה של משטחים שהם לאו דווקא סגורים (כמו פני-כדור, טורוס וביגלה) אלא, למשל, הם בעלי אותה טופולוגיה כמו עיגול מלא - יכולים להיות להם קווי שפה.
להיות אינסופי, להרגיש סופי
אנה ליזהטוב
המתמטיקאי הגדול של תחילת המאה העשרים, דויד הילברט, אמר פעם " הה, האינסוף - המרתק בין המושגים שהמתמטיקאים חוקרים". מה שהילברט התכוון אליו הוא שהאינסוף תמיד מפתיע. למשל, קבוצה יכולה להיות שווה בגודלה לקבוצה שהיא חלקית לה ממש. קבוצה א' יכולה להיות שווה בגודלה לקבוצה ב' שמכילה אינסוף עותקים של א' - אכן מפתיע! אבל יש מקרים שקבוצה היא אינסופית, ומתנהגת כמו קבוצה סופית. התופעה הזאת נקראת "קומפקטיות", והיא לפעמים מועילה.
1. איך צדים אריה על הקטע $latex {[0,1]}$
איך צדים אריה במדבר? יש הרבה שיטות. אחת השיטות היא להגדיר נכון: "לצוד את האריה" פירושו להפריד בינו לבינך על ידי גדר לא עבירה. אם כן, הקף את עצמך בגדר כזו, וצדת.
כאן אני מתכוון לשיטה ידועה אחרת: מחלקים את המדבר לשני חלקים שווים. האריה נמצא באחד מהם. נחלק את החלק הזה לשני חלקים שווים, ושוב האריה נמצא באחד מהם. כשנמשיך לחלק, מהר מאוד נגיע למצב שבו האריה נמצא בחלק קטן מאוד. שפירושו שתפסנו את האריה - הנה הוא, בחלק הקטן שאליו הגענו. מומלץ לא לנסות בבית - אריה הוא בכל זאת חיה מסוכנת.
השיטה הזאת עומדת בבסיסו של משפט מתמטי שנקרא על שמם של בולצאנו ויירשטרס ($latex {Bolzano, ~~Weierstrass}$). הם לא מצאו את המשפט בעבודה משותפת - בסוף המאה התשע עשרה עבודה משותפת עדיין לא הייתה באופנה. הם גילו אותו משפט בנפרד.
נניח שנתונה לכם קבוצה של מספרים, נקרא לה $latex {A}$. נקודה (מספר) $latex {a}$ נקראת "נקודת הצטברות" של $latex {A}$ אם יש לידה אינסוף נקודות מ- $latex {A}$. מה פירוש "לידה"? האם זה מונח מתמטי? לא בדיוק, אבל אפשר להפוך אותו למושג מדויק. הנה ההגדרה המדויקת:
הגדרה 1.1 $latex {a}$ נקראת "נקודת הצטברות" של $latex {A}$ אם כל קטע פתוח שמכיל את $latex {a}$ (קטע כזה נקרא "סביבה של $latex {a}$") מכיל אינסוף נקודות מ-$latex {A}$.
כמובן, כדי של-$latex {A}$ תהיה נקודת הצטברות היא צריכה להיות אינסופית בעצמה. האם לכל קבוצה אינסופית יש נקודת הצטברות? לאו דווקא. למשל, לקבוצת המספרים הטבעיים אין נקודת הצטברות. אין נקודה שבכל סביבה שלה יש אינסוף מספרים טבעיים. הסיבה היא כמובן ש-$latex {A}$ מתפרשת על פני תחום אינסופי - כך יכולות להיות אינסוף נקודות בלי שיצטברו בשום נקודה. משפט בולצאנו וירשטרס אומר שכאשר הקבוצה מוכלת בקטע סופי, אז יש לה נקודת הצטברות. לצורך העניין לא חשוב מהו הקטע הסופי. אם כן, בואו ניקח את הקטע $latex {[0,1]}$.
משפט 1.2 לקבוצה אינסופית שמוכלת בקטע $latex {[0,1]}$ יש נקודת הצטברות בקטע הזה.
ההוכחה די פשוטה, והיא נמצאת בליבו של רעיון ה"קומפקטיות" שהוזכר בתקציר של המאמר. נקודת המוצא שלה היא עקרון שובך היונים, למקרה האינסופי.
2. עקרון שובך היונים האינסופי
עקרון שובך היונים אומר כזכור שאם מחלקים (נאמר) $latex {101}$ עצמים ל-$latex {100}$ סוגים (כלומר יש פחות סוגים מאשר עצמים) אז יש שני עצמים מאותו סוג. פשוט מאוד, לכל הדעות. אבל עקרון שובך היונים האינסופי הוא פשוט עוד יותר:
משפט 2.1 אם מחלקים אינסוף איברים למספר סופי של סוגים, באחד הסוגים יהיו אינסוף איברים.
מדוע? כי אם מכל סוג יש רק מספר סופי של איברים, ומספר הסוגים הוא סופי, יש יחד רק מספר סופי של איברים. סופי + סופי הוא סופי, עובדה שבה אתם משתמשים כל אימת שאתם מחברים מספרים.
3. הוכחת משפט בולצאנו ויירשטרס
ההוכחה משתמשת בעקרון שובך היונים האינסופי וב"שיטת האריה". נחלק את הקטע $latex {[0,1]}$ לשני חלקים שווים על ידי נקודה באמצעו. על פי עקרון שובך היונים האינסופי באחד החצאים יש אינסוף נקודות מ-$latex {A}$. ניקח את החצי הזה, ונחלק אותו לשניים על ידי נקודה באמצעו. שוב, באחד החצאים יש אינסוף נקודות מ=$latex {A}$. נחלק אותו לשניים על ידי נקודה באמצעו, וכולי. הקטעים שבחרנו (אלה שבהם יש אינסוף נקודות מ-$latex {A}$) קטנים והולכים, וכל אחד מהם מוכל בקודמו. קל להוכיח אז שהם "שואפים לנקודה אחת", שפירושו שהקצוות הימניים שלהם והקצוות השמאליים שואפים לאותה נקודה, נקרא לה $latex {x}$. קל גם לראות שכל סביבה של $latex {x}$ מכילה את אחד הקטעים שבחרנו (אלה שמכילים אינסוף נקודות מ-$latex {A}$) - זה נובע מכך שהאורך של הקטעים שואף ל-$latex {0}$. אם כן, הסביבה המדוברת מכילה קטע שמכיל אינסוף נקודות מ-$latex {A}$, אם כן היא עצמה מכילה אינסוף נקודות מ-$latex {A}$, שפירושו ש- $latex {x}$ היא נקדות ההצטברות המבוקשת.
העיקרון הזה, של "לחלק לשני חלקים", או בעצם - למספר סופי של חלקים, ולהשתמש בכך שבאחד מהם יש אינסוף נקודות מסוג נתון, הוא זה שמדריך את המאמר הזה. קוראים לו "עקרון הקומפקטיות".
4. משפט ארדש-דה ברוין
לעקרון הקומפקטיות יש שימושים בקומבינטוריקה אינסופית. אחד המפורסמים בהם הוא משפט של ארדש-דה ברוין ($latex {Erdos-de~Brujn}$) - הפעם זוהי באמת עבודה משותפת. ב-$latex {1951}$, שנת הלידה של המשפט הזה, הייתה עבודה משותפת כבר יותר מקובלת, עקב ההתניידות הגדולה יותר של המדענים, והתקשורת המהירה יותר (אם מדברים על ניידות - לא היה נייד יותר מפול ארדש, שבילה את חייו בנסיעות בין שותפים לעבודה).
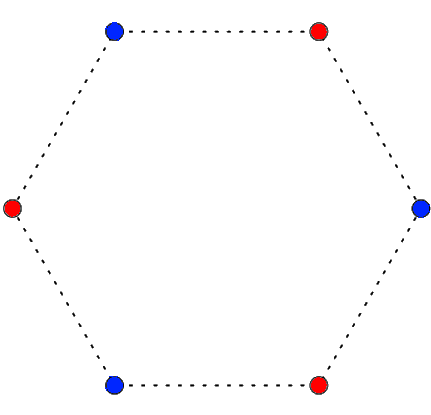
"גרף" הוא אוסף נקודות שנקראות "קדקודים" ואוסף זוגות מתוכם, שנקראים "צלעות". קבוצת קדקודים בגרף נקראת "בלתי תלויה" אם אין בה שני קדקודים שמחוברים בצלע. למשל, בגרף שהוא מעגל באורך 6 הקבוצה המסומנת בעיגולים היא קבוצה בלתי תלויה.
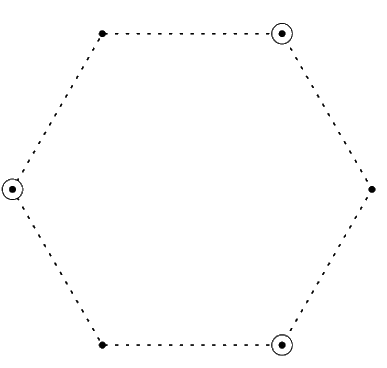
"צביעה" (או "צביעה חוקית") של גרף היא חלוקה של הקדקודים לקבוצות בלתי תלויות. כל קבוצה בלתי תלויה היא "צבע". אם כן, אפשר לנסח את מושג הצביעה גם כך: זוהי חלוקה של הקדקודים לצבעים, כך שכל שני קדקודים באותו צבע אינם מחוברים. למשל, במעגל מאורך 6 יש צביעה ב-2 צבעים, כמו בציור הבא:
 הנה משפט ארדש דה ברוין:
הנה משפט ארדש דה ברוין:
משפט 4.1 אם בגרף אינסופי אפשר לצבוע בצורה חוקית כל קבוצה סופית של קדקודים ב-$latex {k}$ צבעים, אז יש צביעה חוקית של כל הגרף ב-$latex {k}$ צבעים.
בואו נוכיח את המשפט הזה ל-$latex {k=3}$. ההוכחה דומה לכל $latex {k}$. ועוד הגבלה - נוכיח זאת לגרפים ניתנים להימנות, כלומר גרפים שבהם אפשר למנות את הקדקודים כך:
$latex \displaystyle v_1, v_2, v_3, \ldots$
המשפט נכון גם כאשר קבוצת הקדקודים אינה ניתנת להימנות, אבל ההוכחה קצת יותר קשה.
בואו נקרא לצבעים שלנו כ, א ו-צ (כחול, אדום וצהוב).
לפי ההנחה של המשפט יש צביעה חוקית של הקדקוד $latex {v_1}$ )למעשה לא נחוצה כאן שום הנחה - צבעו אותו באיזה צבע שאתם רוצים). לפי אותה הנחה יש גם צביעה חוקית, נקרא לה $latex {C_2}$, של הקדקודים $latex {v_1,v_2}$ (גם זה לא קשה, אם נתונים לכם שלושה צבעים. פשוט צבעו את שני הקדקודים האלה בצבעים שונים).
לפי אותה הנחה יש גם צביעה, נקרא לה $latex {C_3}$, של הקדקודים $latex {v_1,v_2, v_3}$ (גם זה לא קשה, אם נתונים לכם שלושה צבעים. פשוט צבעו כל קדקוד בצבע שונה).
לפי אותה הנחה יש גם צביעה, נקרא לה $latex {C_4}$, של הקדקודים $latex {v_1,v_2, v_3, v_4}$ (הפעם אנחנו באמת זקוקים להנחה. לו כל ארבעה הקדקודים היו מחוברים זה לזה, לא היינו מצליחים לצבוע אותם בצורה חוקית בעזרת שלושה צבעים בלבד. ההנחה אומרת שזה לא קורה).
וכך הלאה - לכל $latex {n}$ יש לפי ההנחה צביעה חוקית $latex {C_n}$ ב-כ, א, צ של הקדקודים $latex {v_1,v_2, \ldots, v_n}$.
יש לנו אינסוף צביעות (כל צביעה רק של חלק מן הקדקודים), ורק שלושה צבעים. אם כן, על פי עקרון שובך היונים האינסופי, יש אינסוף ערכי $latex {n}$ שעבורם הקדקוד הראשון, $latex {v_1}$, צבוע באותו צבע, נאמר כ. כזכור - אנחנו רוצים לצבוע את כל הגרף. אז נצבע את $latex {v_1}$ ב-כ.
מבין אינסוף הצביעות שבהן $latex {v_1}$ צבוע כ יש אינסוף שבהן $latex {v_2}$ צבוע באותו צבע, נאמר צ. נצבע את $latex {v_2}$ ב-צ.
מבין אינסוף הצביעות שבהן $latex {v_1}$ צבוע כ ו-$latex {v_2}$ צבוע צ יש אינסוף שבהן $latex {v_3}$ צבוע באותו צבע, נאמר שוב כ. נצבע את $latex {v_3}$ ב-כ.
מבין אינסוף הצביעות שבהן $latex {v_1}$ צבוע כ ו-$latex {v_2}$ צבוע צ ו -$latex {v_3}$ צבוע כ יש אינסוף שבהן $latex {v_4}$ צבוע באותו צבע, נאמר א. נצבע את $latex {v_4}$ ב-א.
אני חושבת שההמשך ברור, ואין צורך לכתוב אותו בצורה פורמלית. הטענה היא עתה שהצביעה של כל הגרף שאנחנו מקבלים בדרך זו היא חוקית. הדבר נובע מכך ש"חוקיות" נקבעת על פי זוגות, כלומר 2 קדקודים, ו-2 הוא מספר סופי. אנחנו צריכים להוכיח שלכל $latex {i<j}$ אם $latex {v_i}$ מחובר ל-$latex {v_j}$ אז הם צבועים בצבעים שונים. ובניסוח על דרך השלילה, צריך להוכיח שאם $latex {v_i}$ ו-$latex {v_j}$ צבועים שניהם באותו צבע אז הם לא מחוברים.
נניח ששניהם צבועים באותו צבע, נאמר צ. פירוש הדבר הוא שמצאנו תחילה אינסוף צביעות חוקיות שבהן $latex {v_i}$ היה צבוע ב-צ, ומתוכן מצאנו אינסוף צביעות חוקיות שבהן $latex {v_j}$ צבוע צ. הצביעות המדוברות הן כולן חוקיות, ובכולן $latex {v_i}$ ו-$latex {v_j}$ צבועים שניהם ב-צ. החוקיות של הצביעות האלה אומרת ש-$latex {v_i}$ ו-$latex {v_j}$ אינם מחוברים - שהוא מה שרצינו להוכיח.
5. חלוקות לא ידידותיות
בגיליון $latex {13}$ של העיתון הגדרנו מהי חלוקה לא ידידותית של גרף (כאן). זוהי חלוקה של הקדקודים של הגרף לשתי קבוצות, $latex {A}$ ו-$latex {B}$, שמקיימת את התכונה הבאה: כל קדקוד מחובר ללא פחות קדקודים בקבוצה שאינה שלו מאשר לקדקודים בקבוצה שלו.
במאמר בגיליון $latex {13}$ הראינו שבכל גרף סופי יש חלוקה לא ידידותית, ואתגרנו את הקוראים להוכיח שהדבר נכון גם לגרפים אינסופיים שבהם כל קדקוד מחובר בצלעות רק למספר סופי של קדקודים (השערה מפורסמת למדי היא שהדבר נכון לכל גרף ניתן להימנות, כלומר כזה שאפשר למנות את קדקודיו "ראשון, שני, שלישי…": ההשערה אינה נכונה באופן כללי).
הבטחתי לכם להביא הוכחה באחד הגליונות הבאים, ואני מקיים את ההבטחה, לפחות במקרה הניתן להימנות. הנה היא ההוכחה.
נמנה את הקדקודים: $latex {v_1, v_2, v_3, \ldots}$
לכל מספר $latex {n}$ נסמן ב-$latex {G_n}$ את הגרף המושרה על $latex {v_1, v_2, v_3, \ldots, v_n}$. זהו גרף סופי, ולכן יש לו חלוקה לא ידידותית לקבוצות $latex {A_n,B_n}$.
נסתכל על הקדקוד $latex {v_1}$. לכל $latex {n}$ הוא יכול להשתייך ל-$latex {A_n}$ או ל-$latex {B_n}$. לפעמים כך, ולפעמים כך. אבל דבר אחד בטוח - באינסוף מקרים קורה אותו דבר. כלומר, או שבאינסוף מקרים הוא שייך ל-$latex {A_n}$, או שבאינסוף מקרים הוא שייך ל-$latex {B_n}$ )יכול להיות ששני הדברים קורים(. אם $latex {v_1}$ שייך באינסוף מקרים ל-$latex {A_n}$, נשים אותו בקבוצה $latex {A}$. אחרת נשים אותו בקבוצה $latex {B}$.
נניח ששמנו את $latex {v_1}$ בקבוצה $latex {A}$. אז עבור אינסוף $latex {n}$-ים הוא שייך לקבוצה $latex {A_n}$. וכאן בא חלק חשוב בטיעון: נסתכל רק ב-$latex {n}$-ים האלו, ועכשיו נתבונן בקדקוד השני, $latex {v_2}$. באינסוף מן ה-$latex {n}$-ים שבחרנו הוא שייך לאותו סוג קבוצה - נאמר ל-$latex {B_n}$. נשים אז את $latex {v_2}$ ב-$latex {B}$, ונצמצם את תשומת ליבנו לאותם אינסוף $latex {n}$-ים. מתוכם באינסוף מקרים $latex {v_3}$ שייך לאותו סוג - נאמר שמתוכם באינסוף מקרים הוא שייך ל-$latex {B_n}$. נשים אותו אז ב-$latex {B}$. נמשיך כך.
הטענה היא עתה שהחלוקה שקיבלנו, לקבוצות $latex {A}$ ו-$latex {B}$, היא לא ידידותית. כלומר, שכל קדקוד $latex {v}$ מחובר ללא פחות קדקודים מן הסוג שאינו שייך אליו מאשר לקדקודים מן הסוג שלו. אם $latex {v}$ ב-$latex {A}$ אז הוא מחובר ללא פחות קדקוקדים ב-$latex {B}$ מאשר ב-$latex {A}$, וגם להפך. כמובן, הקדקוד שלנו מופיע איפה שהוא ברשימה. נאמר ש-$latex {v=v_k}$. עתה נשתמש בתנאי שהגרף מקיים - שכל קדקוד מחובר רק למספר סופי של קדקודים אחרים. אם כן, קבוצת הקדקודם ש-$latex {v_k}$ מחובר אליהם נמצאת באיזשהו קטע התחלי סופי, נאמר $latex {\{v_1, v_2, \ldots,v_m\}}$.
עכשיו צריך להיזכר איך בחרנו את מיקומו של כל קדקוד. זוכרים?
בחרנו אינסוף $latex {n}$-ים שבהם $latex {v_1}$ ב-$latex {A_n}$;
מתוכם בחרנו אינסוף $latex {n}$-ים שבהם $latex {v_2}$ ב-$latex {B_n}$;
מתוכם בחרנו אינסוף $latex {n}$-ים שבהם $latex {v_3}$ ב-$latex {B_n}$;
$latex {\ldots}$
(מובן, הבחירות המסוימות האלה הן רק לצורך הדוגמה, אבל אין כאן הגבלת כלליות). אם כן יש אינסוף $latex {n}$-ים גדולים מ-$latex {m}$ שעבורם כל הקדקודים $latex {v_1, \ldots, v_m}$ בוחרים אותו דבר - להיות ב-$latex {A_n}$ או ב-$latex {B_n}$,
וכן - הבחירה שלנו אם לשים אותם ב-$latex {A}$ או ב-$latex {B}$ נעשית בהתאם.
אבל כל אחת מן החלוקות $latex {A_n,B_n}$ טובה לגרף המושרה על הקדקודים עד $latex {v_n}$. במיוחד, אם ניקח $latex {n=m}$ (זה נכון לכל $latex {n}$), היא טובה עבור $latex {v_k}$ שלנו. כלומר בגרף המושרה על הקדקודים $latex {v_1, \ldots, v_n}$ הקדקוד $latex {v_k}$ מחובר ללא פחות קדקודים בקבוצה שאינה שלו מאשר לקדקודים בקבוצה שלו.
אבל עבור $latex {n= m}$ השכנים של $latex {v_k}$ בגרף $latex {G_n}$ הם בדיוק השכנים שלו בגרף כולו. אם כן, התנאי נכון גם לגבי שכניו בגרף כולו - שהוא מה שרצינו להוכיח. הוא מכיר לא פחות קדקודים מן הסוג שאינו שלו מאשר מסוגו. זה נכון לכל קדקוד, ולכן החלוקה לא ידידותית.
6. סיכום
גרף שבו כל קדקוד מחובר רק למספר סופי של קדקודים הוא בעל "אופי סופי". ומה שהראינו אז שהוא מתנהג, לפחות מבחינת ידידותיות של חלוקות, כמו גרף סופי. במשפט ארדש דה ברוין הסופיות הייתה אחרת - שם הסתכלנו בתכונה שנקבעת על ידי מספר סופי של קדקודים (במקרה זה - זוגות של קדקודים). וגם שם ראינו שאפשר לעבור מהסופי לאינסופי - מספיק לדרוש את התנאי למספר סופי של קדקודים. זוהי הקומפקטיות.
חידות
דניאל לובזנס
לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 26.6.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1 –מתי יפגשו הכלבים?
ארבעה כלבים נמצאים בארבע פינות של מגרש בצורת ריבוע שאורך צלעו $latex 200$ מ'. הכלבים רצים זה אחרי זה, הכלב בפינה השמאלית התחתונה אחרי זה שבפינה השמאלית העליונה, זה שבפינה השמאלית העליונה אחרי הכלב שבפינה הימנית העליונה, וכן הלאה כמתואר בשרטוט.
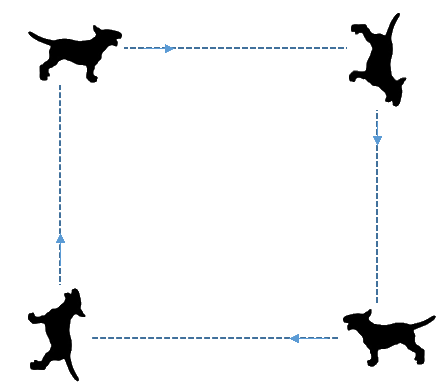
כל אחד מהכלבים ממשיכים לרוץ בכיוון הכלב שאחריו הוא רודף (שמשנה גם הוא את מיקומו בתהליך..) במהירות קבועה של $latex 20$ קמ"ש. האם הכלבים יפגשו כעבור זמן סופי (מדובר ב"כלבים מתמטיים" שגודלם הוא נקודה), ואם כן כעבור כמה זמן? האם יתכן שמסלוליהם יחצו זה את זה?
למחפשי האתגר מבינכם שתי חידות נוספות:
א. מה תהיה התשובה לחידה אם יש שישה כלבים הנצבים בפינות של משושה משוכלל שאורך צלעותיו $latex 200$ מ'?
ב. לאלה מכם היודעים חשבון דיפרנציאלי ואינטגרלי: מה תהיה משוואתו של המסלול שיעשה כל אחד מהכלבים בחידה הראשונה ($latex 4$ כלבים).
חידה 2 –האם נתן לצבוע בשני צבעים?
מצירים במישור $latex n$ מעגלים בגדלים שונים, היקפי העגולים תוחמים מספר שטחים. האם נתן לצבוע כל אחד מהשטחים באחד משני צבעים, כך ששני שטחים הנוגעים זה בזה ע"י קשת משותפת לא יהיו בני אותו צבע. משורטטת דוגמא של $latex 4$ עיגולים המונחים במישור כך שניתן לצבוע את המשטחים בשני צבעים (אדום ולבן, בדוגמא) לפי הדרישות. האם זה אפשרי תמיד? אם לא יש להביא דוגמא נגדית.

חידה 3 –בכמה מספרים מופיעה הספרה אחד?
בין המספרים הטבעיים הקטנים או שווים ל $latex 10,000,000$ ($latex 10$ מיליון) האם יש יותר מספרים המכילים את הספרה $latex 1$ לפחות פעם אחת (למשל $latex 34156$, או $latex 2101132 $) או כאלה שאינם מכילים כלל את הספרה $latex 1$ (למשל $latex 876394$)?
רמזים לחידות מגיליון מאי 2015
חידה 1 –משולשים מחלקים משולש?
שימו לב שהשרטוט המוצג בתחילת החידה הוא השלכה של פרימידה תלת מימדית, גם החידה היא השלכה של גוף משוכלל תלת מימדי.
חידה 2 –מספר בשתי שיטות ספירה?
רשמו את המשוואות למספר הנדרש בשתי השיטות, שימו לב שקל למצוא את ערכה של הספרה האמצעית.
חידה 3 –כמה נורות ידלקו?
בדקו כמה פעמים ילחץ המפסק של הנורה מספר $latex n$. איזו תכונה של המספר $latex n$ מבטיחה מספר לחיצות אי-זוגי?
פתרון החידות גיליון אפריל 2015
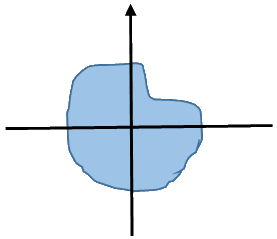
חידה 1 – איך לחלק את הפאי?
ננסה לחלק את הפאי כשהצלב מקביל לצירים הראשיים. כדי לתאר את הכיוונים בצורה חד משמעית נניח לקו הראשון יש כיוון (המתואר בציור כראש חץ) ואז ניתן לדבר באפן ברור על צדיו, השמאלי (זה שנמצא משמאלו כאשר ראש החץ מופנה למעלה) והימני. וצדיו העליון (זה שקרוב יותר לראש החץ) והתחתון
בשלב ראשון נעביר את הקו האנכי כך שיחצה בדיוק את הפאי (זה אפשרי תמיד כי ניתן להזיזו באופן רציף בכיוון האופקי ולהגדיל את החלק השמאלי עד ששטחו יהיה בדיוק מחצית השטח).
כמתואר באיור הבא:

בשלב הבא נעביר קו אופקי כך שיחצה בדיוק את הצד השמאלי:
נסמן את חלקי הפאי באותיות $latex A,B,C,D$ כאשר $latex A$ מסמן את החלק הימני העליון, והשאר את יתר החלקים בכוון השעון.
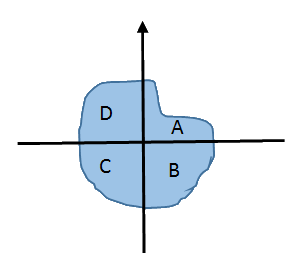
נניח כי שטח הפאי הוא $latex 1$ . נסמן ב $latex S_A,S_B,S_C,S_D$ את שטחי החלקים $latex A,B,C,D$ בהתאמה. ברור מצורת אופן הבניה ש$latex S_C=S_D=\frac{1}{4}$. אם גם $latex S_A=\frac{1}{4}$ הצלחנו לחלק את הפאי ל$latex 4$ חלקים שווים. אם לא, נניח כי $latex S_A<\frac{1}{4}$ ,(למקרה ההפוך ניתן להמשיך בהוכחה דומה עם שינוי מתאים של הסימנים). נסובב את כיוון קווי החלוקה בזווית כל שהיא $latex \theta$ כמתואר באיור הבא:
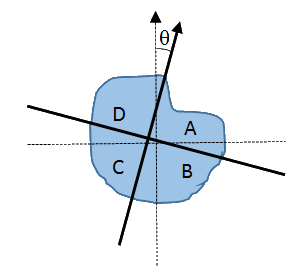
נמשיך ונבצע את הבניה עבור כל זווית $latex \theta$ כאשר $latex 0\le\theta\le90$.
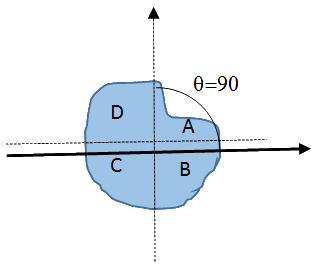
נבחן את הבניה עבור $latex \theta = 90$
קודם כל נעביר את הקו הראשון, שמסומן בחץ, עכשיו הוא אופקי.
קו זה צריך לחצות את הפאי מאחר ו$latex S_A+S_D<\frac{1}{2}$ הקו יעבור מתחת קו האופקי ששורטט למקרה $latex \theta = 0$
כשנעביר את הקו האנכי הוא יצטרך לחלק לשניים את חלק הפאי שמשמאל לקו הראשון (זה עם חץ) כלומר במחצית העליונה של המישור. מאחר והקו אופקי החדש נמוך יותר מהראשון החלק שבפינה העליונה השמאלית גדול מ $latex \frac{1}{4}$ ולכן הקו האנכי חדש ייפול משמאל לקו שהיה עבור $latex \theta = 0$
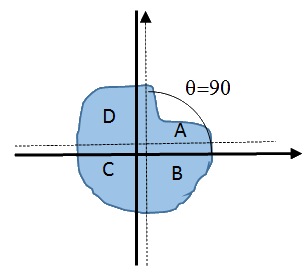
תנו את דעתכם שבשל הסיבוב צריך יהיה לשנות ב $latex 90$ מעלות את מיקומי החלקים $latex A,B,C,D$ ולצורך הבהרה סימנתי אותם כ $latex A’,B’,C’,D’$.
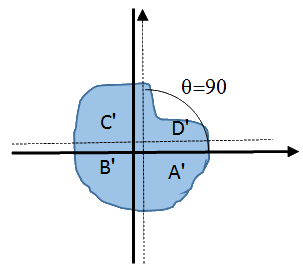
מהציור ברור כי $latex S_{B'}<S_C = \frac{1}{4}$, ולכן $latex S_{A'}>\frac{1}{4}$.
נסתכל על הפונקציה $latex f(\theta) = S_A-\frac{1}{4}$. זו בברור פונקציה רציפה וחסומה. עבור $latex \theta = 0$ ערכה שלילי ואילו עבור $latex \theta = 90$ ערכה חיובי ולכן קימת זווית ( $latex 0\le\theta\le90$ )שבה ערך הפונקציה הוא $latex 0$ כלומר הפאי מחולק בדיוק לארבעה חלקים שווים בשטחם.
חידה 2 – איך לחלק את העוגה? –
לבעיה זו אביא שני פתרונות. הראשון שהכרתי מזה שנים, והשני הוא פתרונו של משה דוידוביץ (לאחר "שפוץ" קל). לבסוף אראה שת שיטתו של Martin Gardner למקרה כללי של חלוקת העוגה בין $latex n$ אנשים.
פתרון 1 -החלוקה מתבצעת בשני שלבים:
בשלב 1 – האיש הראשון יחלק את העוגה לשני חלקים השווים לפי תפיסתו והאיש השני יבחר אחד מהם. נסמן ב-$latex A$ את החלק שיבחר האיש השני וב-$latex B$ את זה שיישאר בידי הראשון.
בשלב 2 – הראשון והשני יחלקו את חלק העוגה שברשותם ל$latex 3$ חלקים שווים לפי תפיסתם. האיש השלישי יבחר לו חלק אחד מחלקו של כל אחד מהם.
כדי להראות באפן פורמאלי שהחלוקה איננה מקפחת נניח שלכל אחד מהאנשים יש שיטת מדידה הנותנת ערך מספרי לעוגה השלמה או לחלק ממנה. נניח גם שערכה של העוגה השלמה הוא $latex 1$ (לפי כל אחת משיטות המדידה), וכי בכל חלוקה של נתח עוגה סכום ערכי החלקים שווה לערכו של הנתח המחולק.
בשלב 1 – איש מספר $latex 1$ מחלק אותה ל$latex 2$ חלקים $latex A$ ו – $latex B$
לפי מדד איש מס' 1 – ערכו של חלק $latex A$ - $latex \frac{1}{2}$ וערכו של חלק $latex B$ - $latex \frac{1}{2}$
לפי מדד איש מס' 2 – ערכו של חלק $latex A$ - $latex X$ וערכו של חלק $latex B$ - $latex 1-X$
לפי מדד איש מס' 3 – ערכו של חלק $latex A$ - $latex Y$ וערכו של חלק $latex B$ - $latex 1-Y$
בלי הגבלת הכלליות נניח כי $latex x\ge\frac{1}{2}$ ולכן איש מס' 2 בוחר את נתח $latex A$.
בשלב 2 – איש מספר 1 מחלק את $latex B$ לשלשה חלקים : $latex B_1,B_2,B_3$ שערך כל אחד מהם לפי מדדו $latex \frac{1}{6}$
איש מספר 2 מחלק את $latex A$ לשלשה חלקים: $latex A_1,A_2,A_3$ שערך כל אחד מהם לפי מדדו $latex \frac{X}{3}$ שהוא גדול או שווה ל$latex \frac{1}{6}$
איש מספר 3- לפי מדדו לפחות אחד החלקים של $latex A_1,A_2,A_3$ גדול או שווה ל$latex \frac{y}{3}$ (כי אם כולם היו קטנים מ$latex \frac{y}{3}$ סכומם היה קטן מ$latex Y$) הוא יבחר בחלק זה. בצורה דומה הוא יבחר בחלק שערכו גדול או שווה ל $latex \frac{1-Y}{3}$ מבין חלקי $latex B$.
כלומר סה"כ לפי מדדיו של איש מס' 3 יהיה לו יותר מ$latex \frac{1}{3}$ ($latex \frac{(1-Y)}{3}+\frac{Y}{3}$). בידי איש מס 1 יישארו $latex 2$ חלקי $latex B$ שערכם לפי מדדו בדיוק $latex \frac{1}{3}$ , ואילו בידי איש מס' 2 יהיו שני חלקי $latex A$ שערכם לפי מדדו גדול או שווה ל$latex \frac{1}{3}$. כלומר כולם לא יחושו מקופחים.
יש לתת את הדעת שהאיש הראשון (שמחלק את העוגה) מקבל תמיד בדיוק את חלקו, בעוד האחרים שבוחרים יכולים בד"כ לקבל קצת יותר ממה שהם חושבים שמגיע להם.
פתרון 2 – עפ"י משה דוידוביץ. החלוקה מתבצעת בשלב או אחד או שניים בהתאם לצורך.
בשלב הראשון:
איש מס' 1 מחלק את העוגה ל$latex 3$ חלקים (שווים לפי תפיסתו)
איש מס' 2 בוחר לו חלק אחד (הכי גדול לתפיסתו ולכן ערכו גדול או שווה ל $latex \frac{1}{3}$)
איש מס' 3 בוחר לו חלק מהשניים הנותרים, וזאת אם יש כזה שאינו קטן מ$latex \frac{1}{3}$ לפי תפיסתו – במקרה זה החלוקה מסתיימת. וברור שכל אחד קיבל, לפי תפיסתו, לפחות שליש מהעוגה.
אם לדעת איש מס' 3 רק החלק שבחר מס' 2 אינו קטן מ $latex \frac{1}{3}$ לפי תפיסתו, הוא מבקש גם כן את אותו חלק ועוברים לשלב השני:
איש מס' 2 בוחר חלק נוסף (הגדול ביותר, לתפיסתו, מבין הנותרים). יש לתת את הדעת שהחלק שנשאר (ויהיה חלקו של מס' 1) קטן או שווה לשליש הן לתפיסתו של איש מס' 2 (כי הוא הקטן ביותר לשיטתו) והן לתפיסתו של מס' 3 (אחרת היה בוחר בו בשלב הראשון).
עכשיו איש מס'2 ומס' 3 מחלקים את $latex 2$ חלקי העוגה שבחר איש מס' 2 ביניהם לשניים בשיטת החלוקה ל-$latex 2$, אחד מהם יחלק והשני יבחר. מאחר והם מחלקים חלק שלדעת שניהם גדול או שווה ל $latex \frac{2}{3}$, מחציתו תהיה גדולה או שווה לשליש ואיש לא יישאר מקופח.
הערה חשובה: יש לתת את הדעת שבשלב הראשון אם איש מס' 3 היה "חמדן" והיה דורש את החלק שבחר מס' 2 כי גם לטעמו הוא היה הגדול ביותר מהשלושה, קיימת סכנה שבשלב השני הוא לא יוכל להבטיח כי יקבל לפחות שליש מהעוגה. הדוגמה הבאה תבהיר את הטענה.
נתונה עוגה במשקל $latex 300$ גר' ועליה $latex 42$ צימוקים ו$latex 42$ דובדבנים. שלושה המחלקים, מס' 1 , 2 ו-3 מעריכים אחרת את העוגה.
מספר 1 מתחשב רק במשקל העוגה (ולכן אם בחלקו יפלו $latex 100$ גר' ומעלה הוא ישמח בחלקו)
מספר 2 מתחשב רק במספר הצימוקים (ולכן אם בחלקו ייפול נתח עם $latex 14$ או יותר צימוקים הוא לא יחוש מקופח)
מספר 3 מתחשב במספר הדובדבנים בלבד (כלומר בחלקה "צודקת" יפלו בחלקו $latex 14$ או יותר דובדבנים).
בשלב הראשון מס' 1 מחלק את העוגה ל$latex 3$ חלקים כל אחד במשקל $latex 100$ גר'. מאחר והוא לא מייחס כל חשיבות לצימוקים ולדובדבנים מספרם אינו זהה בכל החלקים, ובמקרה המעניין הבא נעסוק:
חלק $latex A$ מקושט ב $latex 22$ דובדבנים וב $latex 22$ צימוקים.
חלק $latex B$ מקושט ב $latex 20$ דובדבנים.
חלק $latex C$ מקושט ב $latex 20$ צימוקים.
בשלב הראשון מס' 2 יבחר את חלק $latex A$ וגם מס' 3 , אם יהיה "תאוותן" יבחר באותו חלק.
ולכן יהיה צריך לעבור לשלב הבא שבו מס' 2 יבחר את חלק $latex C$ ויבטיח לעצמו $latex 21$ צימוקים.
מאידך בחלוקה לשתיים של חלקים $latex A$ ו$latex C$ מספר 3 יכול להבטיח לעצמו רק $latex 11$ דובדבנים והוא לא יקבל שליש מחלקו.
כמובן שאם מס' 3 יתנהג לפי האסטרטגיה שהוצעה בפתרון הוא יבחר בחלק $latex B$, וכמובן שלא ירגיש מקופח.
המקרה הכללי – חלוקת עוגה בין $latex n$ משתתפים
קל להכליל את פתרון 1 למקרה הכללי. נשתמש באינדוקציה. נניח ששיטתנו עובדת לחלוקה ל –$latex n-1$ עכשיו כל אחד מ $latex n-1$ האנשים יחלק את חלקו ל$latex n$ חלקים וייתן לאיש מס' $latex n$ לבחור חלק אחד. אני משאיר לקוראים לבדוק שאכן זו חלוקה "צודקת". הבעיה היא שבתהליך העוגה נחלקת ל$latex n!$ חלקים וכבר במספר קטן של משתתפים כל אחד יקבל אוסף של פרורים….
Martin Gardner הציע את השיטה הבאה:
אחד המשתתפים יאחז סכין ויניח אותה סמוך לקצה אחד של העוגה (תחשבו על עוגה מלבנית ארוכה) ולאט לאט יזיז אותה כך שחלק גדול יותר של העוגה ייחשף, המשתתפים יעריכו את גודל החלק (כל אחד לפי תפיסתו) וברגע שהחלק ייראה לאחד מהם מספיק גדול יצעק "חתוך" והאוחז בסכין יחתוך את החלק וימסור אותו. במידה ושניים יצעקו בו זמנית תערך הגרלה ואחד מהם יקבל את החלק – כמובן שגם האוחז בסכין יכול להחליט שהוא מעוניין בחלק ולצעוק "חתוך" כמו יתר המשתתפים. כדי למנוע את נושא הצעקות אפשר גם להציע דרך חלופית שבה כל אחד מהמשתתפים מבקש נתח של העוגה הנחתך במישור במרחק $latex d$ מהקצה שלה (כמתואר בשרטוט). זה שמציע את הערך $latex d$ הנמוך ביותר זוכה בו. השאר ממשיכים בתהליך. כל משתתף שיבחר באסטרטגיה בה הוא יציע $latex d$ שיביא לכך שערך הנתח יהיה, לתפיסתו, $latex \frac{1}{n}$ יקבל בצורה כזו לפחות$latex \frac{1}{n}$ מהעוגה. כי אם לא יקבל את הנתח המבוקש על ידו בשלב הראשון, מובטח לו שנותרו לתפיסתו, יותר מ$latex \frac{(n-1)}{n}$ של העוגה ולכן מובטח לו שבהמשך יוכל לקבל את חלקו. יש לתת את הדעת שמשתתף "חמדן" שינסה לקבל חלק גדול יותר מ$latex \frac{1}{n}$ לא יוכל להבטיח שאכן יקבל אפילו $latex \frac{1}{n}$ מהעוגה.

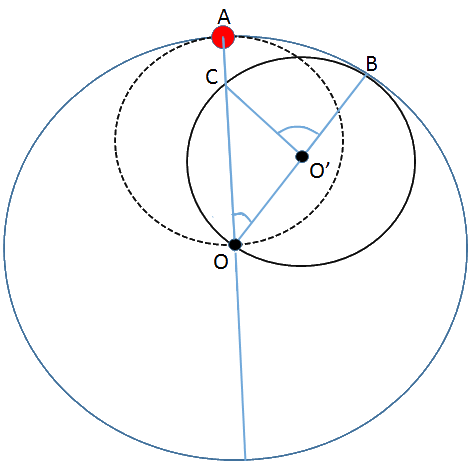
חידה 3 – מסלול? – נראה שהמסלול הוא קו ישר, שהוא קוטר המעגל הגדול העובר דרך הנקודה $latex A$.
נייחס לשרטוט. בקו מקווקו מתואר העגול הקטן במצב שבו הנקודה $latex A$ נמצאת על המעגל הגדול. לאחר סיבוב מסוים מרכז העגול הקטן עובר לנקודה $latex O'$ והוא משיק למעגל הגדול בנקודה $latex B$. נסמן ב$latex C$ את חיתוך המעגל הקטן בקוטר המעגל הגדול $latex OA$ (העובר דרך הנקודה $latex A$). מהמשפט שזווית היקפית שווה למחצית הזווית המרכזית במעגל, נובע כי $latex \angle CO'B = 2*\angle COB = 2*\angle AOB$. מאחר ורדיוס המעגל הגדול כפול מהקטן אורך הקשת $latex AB$ (על המעגל הגדול) שווה לאורך הקשת $latex CB$ (על המעגל הקטן). מאחר והמעגל הקטן נע ללא החלקה בתוך המעגל הגדול הנקודה $latex A$ מגיעה לנקודה $latex C$. כלומר היא נעה לאורך הקוטר. במהלך סיבוב מלא הנקודה $latex A$ תנוע מקצה אחד של הקוטר לקצה השני וחזרה.
שמות הפותרים נכונה את החידות מגיליון מאי 2015
בן בן דוד הולצר, מושב קדרון, כתה י"ב בבי"ס ברנר, בגבעת ברנר. – חידות 2 ו 3
משה דוידוביץ – חידות 2 ו 3
עדי ברשי, כתה ח' בבי"ס רוגוזין ב, קרית אתא–חידה 2