נטגר גליון 17
דבר העורך
רון אהרוני
אחד המתמטיקאים הבולטים בארץ הוא הילל פירסטנברג, שעומד לחגו בספטמבר השנה את יום הולדתו ה- $latex {80}$. אחד מהישגיו המפורסמים הוא פיתוח גישה חדשה ומפתיעה לשאלות בדבר קיום תת סדרות חשבוניות ארוכות בסדרות נתונות. בעזרת הגישה הזאת, למשל, הוכחה לאחרונה השערה עתיקה, שיש סדרות חשבוניות ארוכות כרצוננו של מספרים ראשוניים. בגיליון זה מופיע ראיון של ליזהטוב עם פרופ' פירסטנברג. אפשר ללמוד ממנו הרבה על מה פירוש להיות מתמטיקאי.
כאמור, ההשערה על סדרות חשבוניות של מספרים ראשוניים היא אחת ממשפחת השערות מפורסמות. על המפורסמת ביניהן ידובר במאמר "השערת $latex {3000}$ הדולר". במאמר הזה נספר גם על המשער המפורסם מכולם - פאול ארדש.
מאמר שכתבו גיו יון לי ודורון ציילברגר בהשראת $latex {Joyal}$ ועיבד רון הולצמן על נוסחת קיילי למניית עצים משלים מאמר מגיליון $latex {14}$, של אליהו לוי, על אותו נושא. אחרי שתקראו אותו יהיו בידיכם שתי הוכחות למשפט (יש לו עוד הוכחות רבות).
וכמובן - מדור החידות של דני לובזנס.
תודה לעושים (ולעושות) במלאכה.
הוכחתו של Joyal לנוסחת Cayley
Gyu Eun Lee and Doron Zeilberger, Rutgers University תרגם ועיבד: רון הולצמן, הטכניון
1. קישור ערים ע"י כבישים
נניח שאנחנו מהנדסים הנדרשים לתכנן כבישים שיקשרו בין $latex {n}$ ערים. בשפה מתמטית, הלקוחה מן התחום שנקרא תורת הגרפים, נתונים לנו $latex {n}$ קודקודים (המייצגים ערים), והם מסומנים ע"י המספרים $latex {1,2,\ldots,n}$. אנחנו צריכים להחליט אילו זוגות של קודקודים יחוברו ע"י צלעות (המייצגות כביש ישיר בין שתי ערים). המטרה היא להבטיח שיהיה אפשר להגיע מכל עיר לכל עיר אחרת, לאו דווקא ע"י כביש ישיר ביניהן. בשפת תורת הגרפים, מדובר בגרף קשיר על $latex {n}$ הקודקודים. אפשר כמובן לחבר כל זוג קודקודים ע"י צלע, אבל זה מאוד לא חסכוני $latex {-}$ מספר הכבישים שיידרש הוא $latex {n \choose 2} = \frac{n(n-1)}{2}$.
מהו המספר המינימלי של כבישים המקשרים בין $latex {n}$ ערים? קל להיווכח כי מספר זה הוא $latex {n-1}$. באיור 1 אנחנו מציגים כמה אפשרויות לקשר בין $latex {5}$ ערים ע"י $latex {4}$ כבישים:
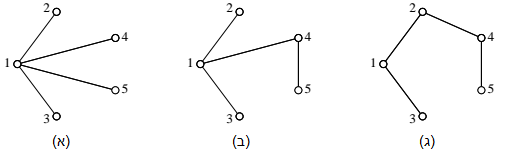איור 1
גרף קשיר על $latex {n}$ קודקודים בעל $latex {n-1}$ צלעות נקרא עץ. כאמור, זה המספר המינימלי של צלעות המאפשר קשירות. בהינתן עץ, לכל שני קודקודים יש דרך אחת ויחידה להגיע מהאחד לשני.
2. עצים מתויגים
בכמה אופנים שונים ניתן לקשר בין $latex {n}$ ערים ע"י $latex {n-1}$ כבישים? לפני שעונים על השאלה, חשוב להחליט אם מייחסים חשיבות לזהותן של הערים. אם כן, אנחנו מדברים על עצים מתויגים (כלומר, לכל קודקוד יש תג המציין את שמו). אם לא, אנחנו מדברים על עצים לא מתויגים.
כדי להבהיר נקודה זו, נתבונן שוב באיור 1. העץ המופיע ב-(א) יכול להופיע ב-$latex {5}$ התגלמויות שונות (בציור קודקוד $latex {1}$ הוא זה שמחובר לכל קודקוד אחר; אבל אפשר לבחור את קודקוד $latex {2}$ להיות זה שמחובר לכל האחרים, או את קודקוד $latex {3}$, וכו'). כאשר מדובר בעצים מתויגים, אנחנו סופרים את $latex {5}$ האפשרויות כשונות זו מזו. כאשר אנו מתעניינים בעצים לא מתויגים, הן נספרות כאפשרות אחת. באופן דומה (עם חשבון מעט יותר מורכב), אפשר להיווכח שקיימים $latex {60}$ עצים מתויגים שהם התגלמויות שונות של איור 1(ב), וכן $latex {60}$ עצים מתויגים שהם בדמותו של איור 1(ג). בסך הכול, יש רק $latex {3}$ עצים לא מתויגים על $latex {5}$ קודקודים, אבל $latex {5+60+60=125}$ עצים מתויגים על $latex {5}$ קודקודים.
נסמן ב- $latex {u_n}$ את מספר העצים הלא מתויגים על $latex {n}$ קודקודים, וב- $latex {a_n}$ את מספר העצים המתויגים על $latex {n}$ קודקודים. הקוראים יוכלו להיווכח בעצמם בנכונות הערכים בטבלה הבאה עבור $latex {n \le 5}$:
| $latex a_n$ | $latex u_n$ | $latex n$ |
|---|---|---|
| $latex 1$ | $latex 1$ | $latex 1$ |
| $latex 1$ | $latex 1$ | $latex 2$ |
| $latex 3$ | $latex 1$ | $latex 3$ |
| $latex 16$ | $latex 2$ | $latex 4$ |
| $latex 125$ | $latex 3$ | $latex 5$ |
מעיון בטבלה, עולה תבנית להתנהגות המספרים $latex {a_n}$. שימו לב שכל ערך של $latex {a_n}$ ניתן לכתיבה כחזקה:
$latex \displaystyle a_1=1=1^{-1}, \quad a_2=1=2^0, \quad a_3=3=3^1, \quad a_4=16=4^2, \quad a_5=125=5^3 $
תבנית זו נראית פשוטה באופן מפתיע, בפרט בהתחשב באופן שבו הגענו למספרים (למשל, $latex {125=5+60+60}$). היא מובילה אותנו לנחש נוסחה כללית עבור $latex {a_n}$:
$latex \displaystyle a_n = n^{n-2} $
מסתבר שנוסחה זו אכן נכונה, והיא קרויה נוסחת קיילי על שמו של $latex {\textrm{Arthur Cayley}}$, שכתב עליה במאמר קצר בשנת $latex {1889}$. התוצאה המקורית היא של $latex {\textrm{Carl Wilhelm Borchardt}}$, שגילה אותה ב-$latex {1860}$. זו נוסחה יפה במיוחד בזכות פשטותה והיותה בלתי צפויה: נדיר בקומבינטוריקה שמקבלים נוסחה כה פשוטה לבעיה לא טריביאלית, ואם בדקתם את ערכי $latex {a_n}$ בטבלה בעצמכם בוודאי תסכימו שהנוסחה בלתי צפויה$latex ^1$. לנוסחת קיילי ידועות הוכחות רבות, ואנו נציג כאן אחת אלגנטית מאוד שניתנה ע"י $latex {\textrm{Andre' Joyal}}$ ב-$latex {1980}$. אבל לפני כן, נידרש לנושא אחר, ונדון בהצגות של תמורות.
3. תמורות ודרכים להציגן
במילים פשוטות, תמורה של קבוצה בת $latex {n}$ איברים היא סדרה שבה מופיעים $latex {n}$ האיברים בסדר כלשהו. יש כמה דרכים מקובלות להציג תמורות.
1.3 כתיבה בשורה אחת
זו כנראה הצורה המוכרת ביותר להציג תמורה. בשורה אחת, תמורה נכתבת ע"י מניית האיברים לפי סדר הופעתם משמאל לימין. למשל, כשמדובר בקבוצה $latex {\{1,2,3,4,5,6\}}$, נכתוב
$latex \displaystyle 341652 $
כאשר נתכוון לתמורה שבה $latex {3}$ מופיע ראשון, $latex {4}$ שני, $latex {1}$ שלישי, $latex {6}$ רביעי, $latex {5}$ חמישי, $latex {2}$ אחרון.
2.3 כתיבה בשתי שורות ופירוק למעגלים
במתמטיקה נהוג לחשוב על תמורה כפונקציה חד-חד-ערכית מקבוצה על עצמה. למשל, בתמורה שנכתבת $latex {341652}$ בכתיב של שורה אחת, הקבוצה היא $latex {\{1,2,3,4,5,6\}}$ והפונקציה מתאימה למקום $latex {1}$ את האיבר $latex {3}$, למקום $latex {2}$ את האיבר $latex {4}$, וכן הלאה. החד-חד-ערכיות של ההתאמה מבטיחה היעדר חזרות בסדרה. הכתיבה בשתי שורות ממחישה את ההתאמה. בשורה העליונה כותבים את האיברים בסדר המקורי, ובשורה השנייה בסדר שנקבע ע"י התמורה:
$latex \displaystyle \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 3 & 4 & 1 & 6 & 5 & 2 \end{pmatrix} $
המשמעות היא $latex {1}$ עובר ל- $latex {3}$, $latex {2}$ עובר ל- $latex {4}$, $latex {3}$ עובר ל- $latex {1}$, וכן הלאה.
היתרון של כתיבה בשתי שורות הוא שהיא מקלה עלינו לעקוב אחר הקורה לאיבר כאשר מפעילים את הפונקציה שוב ושוב. בדוגמה הנ"ל, $latex {1}$ עובר ל- $latex {3}$, ואילו $latex {3}$ עובר ל- $latex {1}$, מה שמחזיר אותנו לנקודת המוצא. בכך גילינו מעגל בתמורה, והוא:
$latex \displaystyle \begin{pmatrix} 1 & 3 \\ 3 & 1 \end{pmatrix} $
כמו כן, $latex {2}$ עובר ל- $latex {4}$, $latex {4}$ עובר ל- $latex {6}$, $latex {6}$ עובר ל- $latex {2}$, ובכך גילינו מעגל נוסף בתמורה והוא:
$latex \displaystyle \begin{pmatrix} 2 & 4 & 6 \\ 4 & 6 & 2 \end{pmatrix} $
נותר האיבר $latex {5}$, אשר עובר לעצמו, וזהו מעגל באורך אחד:
$latex \displaystyle \begin{pmatrix} 5 \\ 5 \end{pmatrix} $
התהליך שתיארנו כאן הוא הפירוק של תמורה למעגלים, שנותן את ההצגה
$latex \displaystyle \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 3 & 4 & 1 & 6 & 5 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 3\\ 3 & 1 \end{pmatrix} \begin{pmatrix} 2 & 4 & 6 \\ 4 & 6 & 2 \end{pmatrix} \begin{pmatrix} 5\\ 5 \end{pmatrix} $
זוהי עובדה בסיסית, שקל להשתכנע בנכונותה, שכל תמורה ניתנת לפירוק למעגלים.
3.3 תיאור גרפי של פונקציות ותמורות
נתבונן כעת בפונקציות כלליות (לאו דווקא חד-חד-ערכיות) מהקבוצה $latex {\{1,2,\ldots,n\}}$ לעצמה. גם פונקציה כזו ניתן להציג בכתיב של שתי שורות, עם אותה מוסכמת כתיבה. למשל:
$latex \displaystyle \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 2 & 1 & 4 & 2 & 4 & 6 \end{pmatrix} $
נוכל לתאר פונקציה ע"י גרף מכוון שבו כל איבר שולח חץ אל תמונתו תחת הפונקציה. הגרף המתאים לדוגמה הנ"ל מופיע באיור 2.
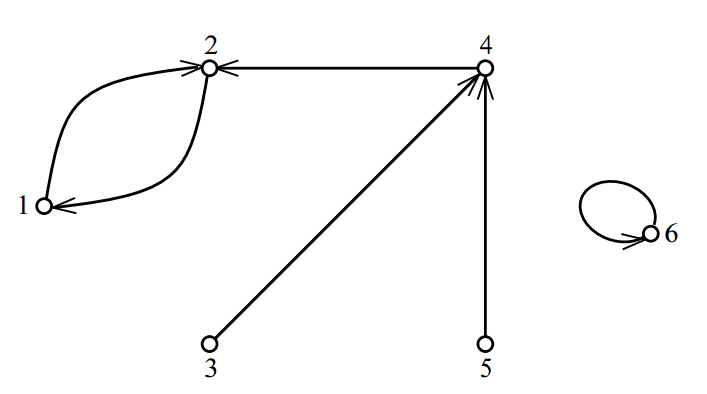
איור 2
נשים לב, שלפי הגדרת מושג הפונקציה, בתיאור הגרפי יוצא מכל קודקוד חץ אחד ויחיד. אם נצא מקודקוד כלשהו ונלך בעקבות החיצים היוצאים, נהיה חייבים במוקדם או במאוחר לבקר שוב בקודקוד שכבר היינו בו. מכאן ברור שהגרף של פונקציה חייב להכיל לפחות מעגל אחד (לצורך העניין, גם חץ מקודקוד לעצמו $latex {-}$ לולאה $latex {-}$ נחשב מעגל). באיור 2, הקודקודים $latex {1}$ ו- $latex {2}$ יוצרים מעגל אחד, והקודקוד $latex {6}$ מעגל נוסף. ייתכן שכל קודקוד נמצא במעגל כלשהו: זהו בדיוק המקרה שבו הפונקציה היא חד-חד-ערכית, כלומר תמורה. במקרה זה מקבלים בצורה גרפית את הפירוק למעגלים של תמורה אשר הוסבר לעיל. אם יש קודקודים שאינם באף מעגל, אז כל קודקוד כזה שולח חץ לקודקוד הנמצא במעגל, או לקודקוד השולח חץ לקודקוד הנמצא במעגל, וכו' (ראו למשל באיור 2).
4. הוכחת ז'ויאל לנוסחת קיילי
כעת אנו מוכנים להוכיח את נוסחת קיילי באמצעות הרעיון המחוכם של ז'ויאל.
משפט. המספר $latex {a_n}$ של עצים מתויגים על $latex {n}$ קודקודים נתון ע"י $latex {a_n = n^{n-2}}$.
הוכחה. תחילה נשים לב שהנוסחה הנתונה שקולה ל- $latex {n^2a_n = n^n}$. הסתכלות זו מועילה, כי $latex {n^n}$ סופר משהו מוכר: זה מספר הפונקציות מ- $latex {\{1,2,\ldots,n\}}$ ל- $latex {\{1,2,\ldots,n\}}$. ומה סופר אגף שמאל? המספר $latex {a_n}$ סופר כמובן את העצים המתויגים על $latex {n}$ קודקודים. נניח שאנו בוחרים שניים מבין הקודקודים של עץ מתויג (אשר יכולים גם להיות אותו קודקוד), וקוראים להם בהתאמה שורש $latex {A}$ ושורש $latex {B}$ של העץ. אפשר לבצע את הבחירות של $latex {A}$ ו- $latex {B}$ ב- $latex {n^2}$ אופנים. לכן $latex {n^2a_n}$ הוא מספר העצים המתויגים על $latex {n}$ קודקודים עם ציון של שני שורשים $latex {A}$ ו- $latex {B}$.
לפיכך, אם נבנה התאמה חד-חד-ערכית ועל בין אוסף הפונקציות מהקבוצה $latex {\{1,2,\ldots,n\}}$ לעצמה, לבין אוסף העצים המתויגים על $latex {\{1,2,\ldots,n\}}$ עם ציון של שני שורשים, ינבע כי $latex {n^2a_n = n^n}$ ובכך תוכח נוסחת קיילי. כלומר, עלינו להראות איך מתאימים לכל פונקציה עץ מתויג עם שני שורשים; ובהינתן עץ מתויג עם שני שורשים איך משחזרים באופן יחיד את הפונקציה ממנה הוא בא.
נתחיל עם פונקציה מהקבוצה $latex {\{1,2,\ldots,n\}}$ לעצמה, ונדגים את בניית העץ המתויג עם שני שורשים המתאים לה עבור הפונקציה מאיור 2. ראשית, מתוך ההצגה של הפונקציה בכתיב של שתי שורות
$latex \displaystyle \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 2 & 1 & 4 & 2 & 4 & 6 \end{pmatrix} $
נשאיר רק את החלקים המעגליים, מבלי לשנות את סדר הופעתם, כלומר
$latex \displaystyle \begin{pmatrix} 1 & 2 & 6 \\ 2 & 1 & 6 \end{pmatrix} $
זוהי כמובן תמורה של תת-קבוצה של $latex {\{1,2,\ldots,n\}}$, שנקרא לה החלק התמורתי בפונקציה. נתבונן בשורה התחתונה שקיבלנו, ונקבע את הקודקוד השמאלי ביותר להיות $latex {A}$ ואת הימני ביותר להיות $latex {B}$ (בדוגמה $latex {A=2, B=6}$). כעת נבנה עץ מתויג עם שני שורשים $latex {A}$ ו- $latex {B}$ כדלקמן. תחילה, נצייר מסילה שלאורכה מופיעים הקודקודים בתמורה לפי סדר הופעתם בשורה התחתונה (בדוגמה $latex {2-1-6}$). קצות המסילה הם $latex {A}$ ו- $latex {B}$ בהתאמה. כעת, נחבר את יתר הקודקודים למסילה בהתאם לחיצים היוצאים מהם בגרף של הפונקציה. התוצאה היא עץ מתויג על $latex {\{1,2,\ldots,n\}}$ עם שני שורשים $latex {A}$ ו- $latex {B}$, והיא מוצגת עבור הדוגמה שלנו באיור 3.
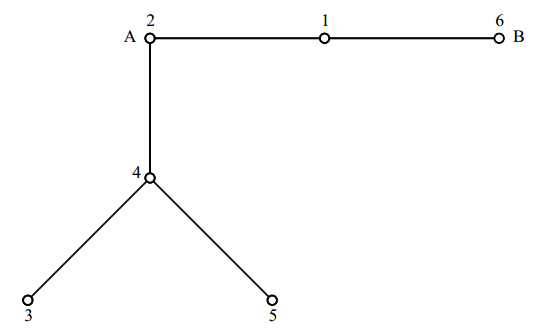
איור 3
ועכשיו, לכיוון ההפוך. נתון לנו עץ מתויג על $latex {\{1,2,\ldots,n\}}$ עם שני שורשים $latex {A}$ ו- $latex {B}$. בעץ יש מסילה יחידה מ- $latex {A}$ ל- $latex {B}$, וממנה נשחזר את השורה התחתונה של החלק התמורתי בפונקציה. (אם $latex {A=B}$, המסילה מורכבת מקודקוד בודד, והחלק התמורתי בפונקציה מורכב מלולאה אחת). ע"י כתיבת אותם קודקודים בשורה העליונה בסדר מספרי עולה, נשחזר את החלק התמורתי בפונקציה. למשל, מהעץ עם שני שורשים באיור 3 נקבל
$latex \displaystyle \begin{pmatrix} 1 & 2 & 6 \\ 2 & 1 & 6 \end{pmatrix} $
כעת, לא נותר אלא להוסיף בשורה העליונה את יתר הקודקודים תוך שמירה על סדר מספרי עולה, ולכתוב מתחת לכל קודקוד כזה את מספרו של הקודקוד הראשון בדרך ממנו אל המסילה $latex {A-B}$ בעץ. בדוגמה נקבל
$latex \displaystyle \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 \\ 2 & 1 & 4 & 2 & 4 & 6 \end{pmatrix} $
שהיא הפונקציה ממנה יצאנו. תהליך השחזור ניתן לביצוע באופן יחיד על כל עץ עם שני שורשים, ובכך עמדנו במשימת ההוכחה. הקוראים מוזמנים לבדוק את הבנת תהליכי הבנייה והשחזור בדוגמאות נוספות, למשל הפונקציה הבאה והעץ עם שני שורשים המתאים לה באיור 4:
$latex \displaystyle \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ 5 & 3 & 1 & 3 & 2 & 3 & 1 & 5 & 5 \end{pmatrix} $
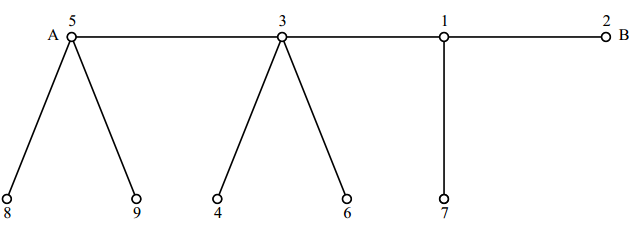
איור 4
$latex ^1$ אותה בעיה לעצים לא מתויגים היא בלתי פתורה, למרות שהמספרים $latex {u_n}$ קטנים בהרבה מ- $latex {a_n}$.
השערת 3000 הדולר של ארדש
אנה ליזהטוב
1. המשער הגדול מכולם
המשער הגדול מכולם, והמפורסם מכולם, היה פול ארדש $latex {(Paul ~~Erdos)}$. הוא שיער בוודאי אלפי השערות, שחלקן זכו לפרסום רב. לפתור השערה של ארדש נחשב לכבוד גדול בין המתמטיקאים. הייתה לו אינטואיציה מופלאה - לא תמיד היה ברור בזמן ניסוח ההשערה מדוע היא חשובה. אבל אם הצהיר על ההשערה שהיא חשובה, בדרך כלל היא התבררה בסופו של דבר ככזו.
כדי לדרג את השערותיו קבע על רוב ההשערות שלו פרסים כספיים. להשערות קלות יחסית הקציב פרס של $latex {10}$ דולר, ולהשערות שחשב שהן קלות באמת (תרגיל למחשבה ליום או ליומיים) הקציב פרסים בפורינטים, המטבע ההונגרי.
השערה בת פרס של $latex {100}$ דולר נחשבה כבר לקשה. השערות בעלות חשיבות מיוחדת זכו לפרס של $latex {1000}$ דולר. ארדש לא טעה אף פעם - לא קרה שהשערה בת $latex {\$1000}$ התבררה כקלה.
ההשערה היקרה ביותר של ארדש שנפתרה הייתה בעלת פרס של $latex {\$10,000}$. היא הייתה שהמספרים הראשוניים מתרווחים לפעמים - שלכל מספר קבוע $latex {C}$ המרחק בין המספר הראשוני ה-$latex {n}$ לבין המספר הראשוני ה-$latex {n+1}$ הוא אינסוף פעמים גדול מ)בערך - הביטוי המדויק מסובך( $latex {C \log n}$. חשבו בעצמכם מדוע אין זה משנה כאן על פי איזה בסיס מחשבים את הלוגריתם. ההשערה הזאת נפתרה ב-$latex {2014}$ על ידי גרין, פורד, קוניאגין וטאו, ובאופן בלתי תלוי על ידי מיינרד.
ההשערה היקרה ביותר מאז ומעולם היא בעלת פרס של $latex {\$25000}$.
הוכיחו שיש רק מספר סופי של מספרים ראשוניים $latex {p}$ המקיימים את התנאי הבא: $latex {p}$ קטן מן הממוצע של המספר הראשוני הקודם לו והמספר הראשוני הבא אחריו.
זוהי השערה קצת מוזרה, כי על הפרכה שלה (כלומר הוכחה שיש אינסוף מספרים ראשוניים המקיימים את התנאי הזה) הפרס הוא רק $latex {\$100}$, שפירושו שכנראה ארדש שיער שאכן יש אינסוף מספרים כאלה, כך שמאוד ייתכן שהפרס הזה לא יינתן.
ההשערה היקרה ביותר שנותרה פתוחה היא בעלת פרס של $latex {\$3000}$. עליה אני רוצה לספר לכם במאמר הזה. אחת הסיבות לכך שאני מזכיר דווקא אותה היא שאורחנו בגיליון הזה, הילל פירסטנברג, תרם רבות להבנתה.
2. סדרות חשבוניות ארוכות בתוך קבוצות של מספרים
האם תוכלו למצוא סדרה חשבונית $latex {a,a+b,a+2b, \ldots ,a+kb}$ בתוך סדרת המספרים $latex {1,2,4,8,16,\ldots}$ (החזקות של $latex 2$)? בוודאי - למשל הסדרה בת שני האיברים $latex {4,32}$ היא סדרה חשבונית. לא ממש חוכמה. אבל האם תצליחו למצוא בסדרה תת סדרה חשבונית עם יותר משני איברים? אשאיר לכם כתרגיל שלא. תת הסדרה החשבונית הארוכה ביותר היא מסדר 2. הסיבה היא שהסדרה דלילה מדי. האיברים לא מספיק צפופים.
מה קורה כשהסדרה צפופה יותר? זו הייתה אחת משאלותיו של ארדש, שנשארה פתוחה במשך זמן רב. איך מודדים צפיפות? זה פשוט: מגדירים גודל שנקרא לו $latex {d(n)}$ (ה-$latex {d}$ הוא כאות הראשונה של $latex {density}$, צפיפות), שהוא מספר האיברים בסדרה הקטנים מ-$latex {n}$, מחולק ב-$latex {n}$.
ההשערה של ארדש וחברו טורן $latex {(Turan)}$ מ-$latex {1936}$ הייתה שאם קיים מספר חיובי $latex {c}$ שלאינסוף ערכי $latex {n}$ מתקיים $latex {d(n)>c}$ אז יש בסדרה תת סדרות חשבוניות ארוכות כרצוננו: יש תת סדרה חשבונית בעלת $latex {3}$ איברים, יש תת סדרה חשבונית בעלת $latex {3}$ איברים, וכו'. למשל, המספרים האיזוגיים מקיימים את התנאי המדובר, עם $latex {c=\frac{1}{2}}$. ואכן, במספרים האיזוגיים תוכלו למצוא תת סדרות חשבוניות ארוכות כרצונכם. למעשה, זוהי סדרה חשבונית בעצמה.
ב-$latex {1953}$ הוכיח רוט שבסדרה כזו יש תת סדרה חשבונית מאורך $latex {3}$. את ההשערה כולה הוכיח סמרדי $latex {(Szemeredi)}$ ב-$latex {1975}$. ב-$latex {1977}$ נתן הילל פירסטנברג הוכחה שמתשמשת בכלים לא אלמנטריים, מתחום שנקרא "תורה ארגודית". זה היה פתח להתקדמויות מרחיקות לכת.
3. הכללה
האם נחוץ באמת ש-$latex {d(n)}$ יהיה גדול ממספר קבוע אינסוף פעמים? האם לא מספיק תנאי צפיפות חלש יותר? את השאלה הזאת שאל ארדש את עצמו ואת העולם. התנאי שהציע הוא שסכום ההופכיים של איברי הסדרה הוא אינסופי - מה שאומר שיש "הרבה" מספרים בסדרה. הוא הציע את ההשערה הבאה, שלה הציב כפרס $latex {3000}$ דולר: אם $latex {a_1,a_2, \ldots,}$ היא סדרה המקיימת $latex {\sum_{i <\infty}\frac{1}{a_i}=\infty}$ אז יש בסדרה סדרות חשבוניות ארוכות כרצוננו.
אילו סדרות מקיימות את התנאי הזה? למשל, סדרת הריבועים אינה מקיימת אותו. קל להוכיח (קחו זאת לעצמכם כתרגיל לחשיבה) ש-$latex {\sum_{i<\infty}\frac{1}{i^2}}$ כלומר $latex {\frac{1}{1}+\frac{1}{4}+\frac{1}{9}+\ldots}$ הוא סופי. אוילר אפילו הצליח לחשב את הסכום הזה, ולהראות שהוא שווה ל-$latex {\frac{\pi^2}{6}}$ (מפתיע, לא?).
יש סדרת מספרים חשובה שסכום ההופכיים שלה הוא אינסופי: סדרת המספרים הראשוניים.
$latex \displaystyle \sum_{i<\infty}\frac{1}{p_i}=\frac{1}{2}+\frac{1}{3}+\frac{1}{5}+\frac{1}{7}+\frac{1}{11}+\ldots=\infty$
נסו להוכיח זאת. אם לא תצליחו - כתבו לנו, ונפרסם את הפתרון באחד הגליונות הקרובים. על כל פנים, אם השערתו של ארדש נכונה כי אז אפשר למצוא סדרות חשבוניות ארוכות כרצונכם של מספרים ראשוניים. קל למצוא סדרה חשבונית באורך $latex {3}$ שכל איבריה ראשוניים - $latex {3,7,11}$. האם אתם יכולים למצוא סדרה חשבונית כזו באורך $latex {4}$? לגמרי לא פשוט.
ההשערה שבמספרים הראשוניים יש סדרות חשבוניות ארוכות כרצוננו הייתה פתוחה כמאתיים שנים. היא נפתרה לבסוף על ידי גרין וטאו ($latex {Green, ~Tao}$) ב-$latex {2004}$. ההשערה הכללית יותר של ארדש עדיין פתוחה לרווחה. אין יודעים אפילו שבתנאי של ארדש יש בהכרח תת סדרה חשבונית באורך $latex {3}$.
ראיון עם פרופ' הילל פירסטנברג
אנה ליזהטוב
- מתי נוכחת לדעת שאתה רוצה להיות מתמטיקאי?
כשלמדתי בבית הספר התיכון (שליד אוניברסיטת Yeshiva University) הבנתי שאם אוכיח שקיומו של המספר $latex i$ (שורש של $latex -1$) מוביל לסתירה, זה יהיה הישג גדול. אז מילאתי מחברת אחרי מחברת של רשימות מתוך תקווה להגיע לסתירה. באותו זמן נהניתי עמוקות מן הגיאומטריה של בית הספר התיכון. לא היו לי מחשבות על מקצוע לעתיד. הייתי בטוח שאני עומד להיות רב. במשך לימודי בתיכון עברתי על פני כל ספרי החשבון הדיפרנציאלי והאינטגרלי בספריה השכונתית, כך שכאשר הגעתי לאוניברסיטה הייתי פטור מן המקצוע הזה. במקום זה למדתי גיאומטריה פרויקטיבית ואת נושאי החובה למדתי בעצמי.
לאוניברסיטה שבה למדתי, "אוניברסיטת ישיבה", הייתה ספרייה טובה, כך שלמדתי את רוב הנושאים בעצמי. באותה עת השתנתה מדיניות המוסד ומי שהלך ללימודי רבנות היה צריך לזנוח את כל שאר המקצועות. מכיוון שלא רציתי לעזוב את לימודי המתמטיקה, בחרתי ללמוד לתואר גבוה במתמטיקה. לכן עברתי לאוניברסיטת פרינסטון.
- מהם הסיפוקים של חיי המתמטיקאי? האם יש גם חסרונות?
אחד הסיפוקים הוא עבודה בצוות, שבה שני מוחות מתאחדים לעבודה משותפת. על מישור אחר, המתמטיקאי מוערך על ידי הקהילייה האינטלקטואלית כולה. המונח "הוכחה מתמטית" מתייחס לצורת ידע שבה אין שום מקום לאי וודאות, מה שלא קיים ברוב תחומי הידע האחרים. החיסרון הבולט לעין הוא אי האפשרות לתקשר בדבר עבודתך עם העולם הרחב. ויש כמובן הסיפוק שבתהילה: הערכה של הקהילייה המתמטית. את הסיפוק הזה חוויתי לראשונה כאשר שני מאמרים שלי (האחד מהם מוזכר במאמר על "השערת 3000 הדולר" בגיליון זה - א.ל) פורסמו בעיתונים בעודי סטודנט.
- האם היה מתמטיקאי מסוים שהשפיע על עבודתך?
הגיבורים המתמטיים שלי היו נורברט וינר, אנדרה ויי וישראל גלפנד. וינר היה אחראי להתעניינות שלי באנליזה הרמונית (ייצוג פונקציות כסכום אינסופי של פונקציות גל – א.ל). גלפנד עורר בי את ההערכה לחשיבה אלגברית בתחומי הגיאומטריה והאנליזה (אנליזה היא התחום שהתפתח מן החשבון הדיפרנציאלי והאינטגרלי – א.ל.). אנדרה וייל לא השפיע על עבודתי ישירות, אבל ההוכחה שלו של השערת רימן לשדות של פונקציות וההשערות המדהימות שלו שקישרו טופולוגיה עם תורת המספרים פיתחו אצלי את החוש האסתטי במתמטיקה.
ההשפעה הגדולה ביותר עלי באה ממתמטיקאי ידוע פחות ששימש לי כמדריך ומלווה במשך שנים רבות. זה היה סימור הבר, שסיים את עבודת הדוקטורט שלו כאשר הייתי תלמיד לתואר הראשון. העניין שלי בפונקציות כמעט מחזוריות בא ממנו ומההתלהבות שלו מן התחום. הרבה מן הטעם המתמטי שלי התפתח בהשפעתו.
- מה היו נקודות המפנה בקריירה שלך?
היו לפחות שתיים. הראשונה כאשר כתלמיד תיכון פתרתי, במקביל לחבר, בעיה גיאומטרית קשה במיוחד. הראינו את הפתרונות שלנו לעורך עיתון שפעל באוניברסיטת ישיבה שהייתה מחוברת לתיכון שבו למדתי. עורך העיתון, יקותיאל גינזבורג, היה אדם נדיב, וכשלמד שיש במשפחתנו בעיות כלכליות (אמי הייתה אלמנה) הוא סידר לי משרה בעיתון, וגם השיג לי מלגה דרך יהודי עשיר. הדבר אפשר לי להקדיש את זמני למתמטיקה. במשרה שלי בעיתון הייתי צריך לתרגם מאמרים, וכך למדתי צרפתית וגרמנית, וכמובן גם מתמטיקה.
נקודת מפנה נוספת הייתה שנים רבות אחר כך, כאשר הייתי בשבתון בפרינסטון (עבדתי אז באוניברסיטת מינסוטה). מה שגיליתי שם הוא שתורת המספרים היא עדיין מלכת המתמטיקה (אמרה של גאוס – א.ל). החלטתי אז להתרכז בבעיות שקשורות בתורת המספרים.
- מה מקומו של היופי בעבודתך?
אני חושב שכל מתמטיקאי חש את היופי של המתמטיקה, שיכול להיות טמון בנוסחה יפה, כמו נוסחת אוילר לקשר בין $latex e^{\pi i}=-1$ , או בהוכחה, או אפילו בניסוח של משפט. פשטות וטבעיות הם רכיבים של "יופי", ואלו הם דברים שאני תמיד מנסה להשיג. תופעה שאני מוצא בה יופי היא שרעיונות מתחום אחד עוברים לתחום אחר, מרוחק. יש מכתב ידוע של אנדרה וייל לאחותו סימון, מ-1940, על "אנלוגיות במתמטיקה". גם הוא רואה בשילוב של תחומים שונים את אחד ממקורות היופי של המתמטיקה. (למתעניינים - http://www.ams.org/notices/200503/fea-weil.pdf)
- אילו חוויות ילדות השפיעו עליך ביותר?
לעובדה שהייתה לי אחות גדולה ממני ב-3 שנים היה תפקיד מכריע בהתפתחותי כמתמטיקאי. כשהכיתה שלי למדה חיבור, היא לימדה אותי כפל, ותמיד דאגה שאהיה לפני הכיתה. אחר כך המשכתי להקדים את הכיתה, בעזרת הספרייה הציבורית.
חידות
דניאל לובזנס
לקוראי שלום,
החודש אני שוב מאוכזב. פרט לניסיון, לצערי לא מוצלח, לענות על אחת החידות, אף אחד לא ניסה לשלוח פתרון. אשמח לתגובותיכם, אפילו אלו שלא יכללו פתרונות מלאים, וזאת על מנת שאוכל לכוון את החידות שלא יהיו קשות מדי, אך עדיין מספיק מאתגרות.
לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 28.7.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1 –חלוקת משולש קהה זווית למשולשים חדי זווית?
האם ניתן לחלק כל משולש קהה זווית למספר סופי של משולשים חדי זווית (שכל זוויותיהם קטנות מ-90 מעלות)?
אם כן יש להראות את שיטת החלוקה, אם לא יש להוכיח שזה בלתי אפשרי.
חידה 2–51 מספרים?
הראו כי בכל קבוצה של 51 מספרים טבעיים, קיימים שני מספרים שסכומם או הפרשם מתחלק ב 99 ללא שארית.
חידה 3–האם הנמלים יישארו על המקל?
100 נמלים מפוזרות באפן שרירותי על מקל באורך 5 מטר. חלקן פונות ימינה וחלקן שמאלה. כל נמלה נעה במהירות קבועה של 1 ס"מ לשנייה. כששתי נמלים נפגשות הן הופכות את כוון תנועתן וממשיכות לנוע בכוון ההפוך במהירות של 1 ס"מ לשנייה. נמלה שמגיעה לקצה המקל, נופלת ואינה יכולה לחזור למקל.
האם בסופו של דבר כל הנמלים יפלו מהמקל? ואם כן מהו הזמן המקסימלי שעדיין יוכלו להישאר נמלים על המקל?
רמזים לחידות מגיליון יוני 2015
חידה 1 –מתי יפגשו הכלבים?
שימו לב לסימטריה. מה תוכלו לאמר על מיקומם היחסי של ארבעת הכלבים בכל נקודת זמן.
חידה 2 –האם נתן לצבוע בשני צבעים?
נתן לצבוע בשני צבעים ההוכחה באינדוקציה.
חידה 3 –בכמה מספרים מופיעה הספרה אחד?
חשבו איזה חלק מהמספרים מכיל רק את הספרות 2,3,4,5,6,7,8,9,0 בספרה הראשונה? איזה חלק מכיל אותם בשתי ספרות וכן הלאה..
פתרון החידות גיליון מאי 2015
חידה 1 –משולשים מחלקים משולש?
שימו לב שהשרטוט המוצג בתחילת החידה הוא השלכה של פרימידה תלת מימדית, הצורה המבוקשת בחידה היא השלכה של עשרימון (icosahedron) גוף משוכלל הבנוי מ 20 משולשים שווי צלעות.
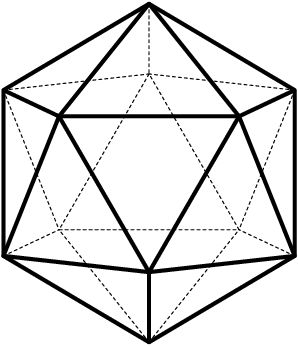
השרטוט הבא הינו השלכה על המישור, של העשרימון. כדי לבצע את ההשלכה מניחים את העשרימון על המישור (אחד המשולשים נמצא במישור) ומנקודה הנמצאת מעל, וסמוך למרכז המשולש המקביל למשולש הנמצא במישור, מותחים קווים ישרים דרך כל קדקודי העשרימון, וכך מסמנים את הטלי כל הקדקודים. היטלו של המשולש העליון, הוא המשולש החיצוני שאותו מחלקים בחידה, והיטלי 19 הפאות הנוספות הם 19 המשולשים ש"מחלקים" את המשולש החיצוני. בכל קדקוד נפגשים בדיוק 5 מקצועות.
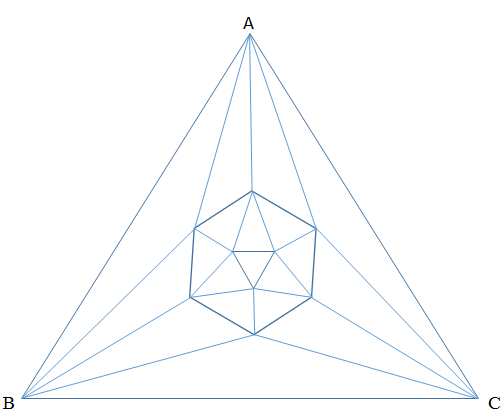
נראה כי אי אפשר לחלק משולש בצורה המבוקשת עבור יותר מ - 19 משולשים.
הוכחה: לצורך ההוכחה נניח כי גם סופרים במניין המשולשים את המשולש החיצוני ABC. כלומר במקרה שלנו מספר המשולשים הוא 20 מספר המקצועות הוא 30 ומספר הקדקודים 12. לכל גרף מישורי קשור נכונה נוסחת אוילר V+F-E=2 כאשר V הוא מספר הקדקודים (במקרה שלנו 12), F מספר הפאות (במקרה שלנו 20 משולשים) ו-E הוא מספר המקצועות (במקרה שלנו 30). לנוסחה זו מספר הוכחות, הפשוטה שבהן היא ע"י הקטנה של מספר המקצועות והקדקודים, כאשר בכל שלב נתן להראות שהסכום V+F-E אינו משתנה. (אני משאיר לקוראי לנסות ולהוכיח את הנוסחה, או לקרוא ולהבין את אחת ההוכחות, אחרים יכולים לדלג על ההוכחה המפורטת ולהסתפק בידיעה שזו נוסחה נכונה ומוכחת).
נניח שבכל קדקוד נפגשים בדיוק k מקצועות. מאחר ומדובר במשולשים שלכל אחד שלושה מקצועות הקשר בין מספר המשולשים למספר המקצועות הוא:
$latex F=\frac{E*2}{3}$ הגורם 2 נובע מכך שכל מקצוע שייך לשני משולשים (זה נכון גם לקווים החיצוניים כי גם המשולש ABC נספר).
כמוכן הקשר בין מספר הקדקודים ומספר המקצועות הוא:
$latex v=\frac{E*2}{k}$
נציב קשרים אלו בנוסחת אוילר ונקבל:
$latex \frac{E*2}{k}+\frac{E*2}{3}-E=2$
מכן נחשב את E
$latex E=\frac{6*k}{6-k}$
מנוסחה זו קל לראות כי כדי שמספר המקצועות יהיה חיובי וסופי נדרוש k<6.
במקרה שלנו k=5 המביא ל E=30 ולכן ל- F=20 המתאים לחלוקת המשולש ל 19, לחלוקה למספר גדול יותר לפי התנאים יידרש k גדול יותר וזה בלתי אפשרי. הקוראים מוזמנים לבדוק מה קורה עבור המקרים k=2,3,4 .
חידה 2 –מספר בשתי שיטות ספירה?
יהיו ספרות המספר המבוקש x,y,z מרישום ערך המספר המתקבל בשתי שיטות הספירה נקבל:
$latex 81*x+9*y+z=49*z+7*y+x$
אחרי העברה בין האגפים וחלוקה ב 2 נקבל:
$latex y=24*z-40*x$
כלומר y מתחלק ב 8, מאחר וזו ספרה גם בשיטת 7 אזי y<7 ולכן y=0
מכאן נקבל: $latex 3*z=5*x$ משוואה שפתרונה בדרישה x<7 z<7 הוא z=5 x=3.
כלומר בשיטת 7 המספר הוא 503 ובשיטת 9 הוא 305. (בשיטה העשרונית המקובלת המספר הוא 248)
חידה 3 –כמה נורות ידלקו?
כל לחצן ילחץ מספר פעמים כמספר המחלקים שלו. למשל הלחצן מספר 138 מתחלק ב 1,2,3,6,23,46,69,138, ולכן יילחץ 8 פעמים. בד”כ למספר n מספר מחלקים זוגי כי אם k מחלק את n אז גם n/k מחלק את n . היוצאים מהכלל הם הרבועים השלמים כי אם $latex n=m^2$ אז $latex m=\frac{n}{m}$. כלומר לריבועים השלמים יש מספר מחלקים אי זוגי. למשל מחלקי 100 הם:1,2,4,5,10,20,25,50,100 . יש 31 רבועים שלמים הקטנים מ 1000 ולכן 31 נורות ידלקו בסוף התהליך, כי לחצניהן יילחצו מספר אי זוגי של פעמים.