נטגר גליון 18
דבר העורך
החודש חוזרים אלינו מכרים ישנים. האחד הוא הספר ״מתמטיקה, שירה ויופי״, שממנו בחרנו הפעם להביא פרק על סימטריה ־ במתמטיקה ובשירה. סימטריה היא דרך לחסוך (ומתמטיקה אוהבת כידוע חיסכון) ־ מראה עושה לנו חצי מן העבודה.
יש גם מאמר שנלקח מ״גליונות מתמטיקה״, על מספרים האלגבריים. הכותב הוא פרופ׳ לויצקי ז״ל, מראשוני האלגבראיסטים בארץ. הנושא הוא מספרים אלגבריים, כלומר מספרים שהם פתרונות של משוואות פולינומיאליות עם מקדמים שלמים. האם אתם מכירים מספרים לא אלגבריים? התשובה היא ״כן״, אבל אולי לא ידעתם שהם לא אלגבריים: המספרים הלא אלגבריים המפורסמים ביותר הם $latex \pi$ ו־$latex e$.
מתמטיקאי גדול נוסף שתרם לעיתון (גם כן לאחר מותו) הוא פול ארדש, שאהב מספרים וגיאומטריה כמעט במידה שווה. הייתה לו יכולת ייחודית למצוא בעיות מרתקות אלמנטריות. במאמר שלו הוא מספר על בעיות כאלה בגיאומטריה.
וכמובן, מדור החידות של דני.
אנחנו נפרדים בצער מאורי פרץ, שבנה את האתר והיה אחראי לו מאז היווסדו של נטגר לפני כמעט שנתיים. אורי מתגייס לצבא הקבע, והוא עוזב אותנו ־ אנחנו מודים לאורי על העבודה המקצועית והמסורה. את מקומו יחליף מיכאל ליטבק.
בברכת הנאה, המערכת.
סימטריה
Tyger! Tyger burning bright
In the forests of the night
What immortal hand or eye
Could frame thy fearful symmetry.
("Songs of innocence
and experience", William
Blake)
הוֹ נָמֵר זוֹהֵר שֶׁל לֵיל
זָע בַּיַּעַר הָאָפֵל
אֵיזוֹ יָד יָצְרָה אוֹתְךָ
כֹּה נוֹרָא הוּא תָּאֳמְךָ.
("שירים של תמימות וניסיון",
ויליאם בלייק)
חיסכון על ידי סימטריה
במקראת בית ספר שהייתה לי בילדותי היה סיפור על מלך שהפקיד בידי שני ציירים את צביעתו של אולם המלכות, צד אחד של האולם בידי כל אחד מהם. צייר אחד עמל וטרח במשך חודשים, ואילו חברו ישב ונח. ביום האחרון, לאחר שהראשון סיים את עבודתו, התקין הצייר השני מראות בצד שלו. בא המלך, והתפעל מן הציורים בצד האחד. כשהגיע אל הצד השני, הראה לו הצייר השני שגם בצד שלו יש ציורים נאים, בדיוק באותה מידה. המלך שילם לצייר הראשון את שכרו, ואילו לשני אמר – הנה, אתה רואה במראָה את השטרות שאני נותן לחברך? אתה יכול לקחת אותם בצד שלך.
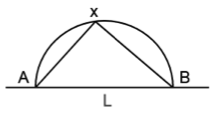
מתמטיקאים דווקא אוהבים מאוד את תחבולתו של הצייר השני. המתמטיקה לעולם אינה חוסכת במאמץ כדי להשיג חיסכון במאמץ, והיא משתמשת פעמים רבות בתחבולת הסימטריה, בהצלחה רבה. אין צורך לעמול פעמיים כשאפשר להסתפק בפעם אחת. לפעמים אחרי השיקוף במראָה קל יותר לראות את הדברים. הנה דוגמה ידועה. שני אנשים, א' ו-ב', נמצאים באותו צד של נחל $latex L$. זהו נחל מתמטי, כלומר הוא קו ישר. אדם א' נמצא בנקודה $latex A$, ואדם ב' בנקודה $latex B$. ב' גווע בצמא, ו-א' רוצה להביא לו מים מן הנחל, מהר ככל האפשר. א' צריך אפוא להגיע ל-$latex L$, ומשם לנקודה $latex B$ שבה נמצא ב'. איזה מסלול יבחר כדי שדרכו תהיה קצרה ביותר? כלומר, מהו הקו הקצר ביותר שנוגע ב-$latex L$, ומחבר את $latex A$ עם $latex B$? כדי להשיב על השאלה, נשקף את $latex B$ ביחס ל-$latex L$ ונקבל נקודה $latex B'$.

הקו הקצר ביותר המחבר את $latex A$ עם $latex B'$ הוא קו ישר. הקו הקצר ביותר מ-$latex A$ ל-$latex B$ שנוגע בנחל מתקבל משיקוף חלק מן הישר הזה, החלק שנמצא בתוך הנחל.
כל קו המחבר את $latex A$ עם $latex B$ ופוגש את $latex L$ מתאים, כמו באיור, לקו בעל אותו אורך המחבר את $latex A$ עם $latex B'$. הקו הקצר ביותר המחבר את $latex A$ עם $latex B'$ הוא קו ישר. וכך יש דרך למצוא את הקו המבוקש בין $latex A$ ל-$latex B$: חברו את $latex A$ ל- $latex B'$ בקו ישר, ושקפו ביחס ל-$latex L$ את החלק של הקו הזה הנמצא בצד של $latex B'$. קל לראות שבקו המתקבל "זווית הפגיעה" $latex \alpha$ שווה ל"זווית ההחזרה", $latex \beta$. לכך יש שימוש פיזיקלי. עקרון ה"מינימיזציה של האנרגיה" אומר שקרן אור עוברת בין שתי נקודות (גם אם מדובר בהחזרה ממראה) בדרך הקצרה ביותר: גם הטבע "חוסך". מכאן נובע החוק המוכר מן האופטיקה, שזווית ההחזרה של קרן אור ממראָה שווה לזווית הפגיעה שלה.
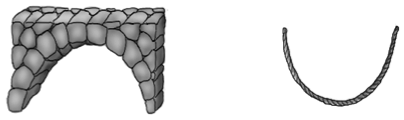
עוד דוגמה לחיסכון על ידי שיקוף היא הדרך לבנות קשת. הרומאים היו אלו שהכניסו את הקשת כאלמנט בסיסי בבנייה. כידוע, הרומאים לא היו מחדשים גדולים, ואת תרבותם שאלו מן העמים שהכניעו, במיוחד מן היוונים. את השימוש בקשת בבנייה הם שאלו מן האטרוּסקים, תושבי איטליה שקדמו להם. זוהי אכן המצאה מפליאה – לבני בניין המחזיקות את עצמן, ללא צורך במלט מחבר. בקשת האידיאלית הלחץ על כל אחת מן האבנים הוא קטן ככל האפשר, ופירושו הדבר הוא בין השאר שהלחץ מתחלק שווה בשווה, כלומר על כל אבן מופעל אותו לחץ. בקשת מעגלית, שהיא אולי הטבעית ביותר וגם הנפוצה ביותר, התנאי הזה אינו מתקיים, שכֵּן הלחץ גדול יותר על הלבנים הנמצאות בצידי הקשת מאשר על אלה שבאמצעה. מהי אם כן הצורה הנכונה? אפשר להשיב על כך בעזרת חישובים, שבכלים המתמטיים של ימינו אינם מסובכים במיוחד (הכלי הנחוץ כאן הוא משוואה דיפרנציאלית). אולם יש גם דרך הרבה יותר פשוטה, שנמנעת מחישובים, והיא לתת לטבע לעשות זאת. במקום להעמיד קשת, לתלות חבל. קחו חבל באורך של הקשת המבוקשת, ותלו אותו בשתי נקודות שמרחקן כמרחק בין קצוות הקשת. החבל יסתדר בצורה שבה מתחלק המתח שווה בשווה בין כל נקודותיו. עתה כל מה שצריך לעשות הוא להפוך את החבל, כך שהקשת שלו תהיה כלפי מעלה. האדריכל הספרדי גאודי השתמש בעיקרון הזה כדי לתכנן את בנייניו.
משחק השולחן העגול
הנה משחק לשני שחקנים. לפניהם שולחן עגול, ובידי כל אחד מהם מלאי בלתי מוגבל של מטבעות של חצי שקל. כל אחד שם בתורו מטבע אחת, במקום פנוי לגמרי, כלומר אסור לשתי מטבעות לחפוף. כלל הניצחון הוא שהמנצח הוא מי שהניח את המטבע האחרונה, כלומר שלאחר שעשה את מסעו אין לשני מקום לשים מטבע. איזה שחקן יכול להבטיח לעצמו זכייה?
התשובה היא שלשחקן הראשון יש אסטרטגיית זכייה. הוא מציב מטבע בדיוק במרכז השולחן. לאחר מכן עליו לנקוט ב"אסטרטגיית מראה" (או "אסטרטגיית קוף"): על כל מטבע שמניח השחקן השני במקום כלשהו, עליו להניח מטבע בדיוק במקום הסימטרי לו ביחס למרכז. האסטרטגיה הזאת מבטיחה שלאחר כל צעד שלו מצב המטבעות הוא סימטרי, כלומר מול כל מטבע יש מטבע. הדבר מבטיח לו זכייה, משום שתמיד יש לו מה להשיב. מכיוון שמצב השולחן סימטרי, אם יש לשחקן השני מקום פנוי, יהיה גם מקום פנוי לראשון, בדיוק ממול.
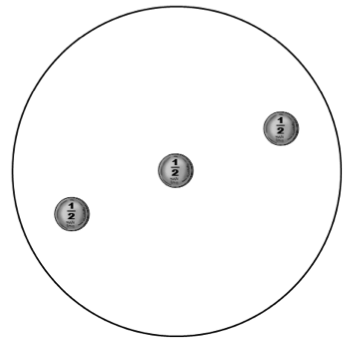
השחקן הראשון שם את המטבע האמצעית. עתה, על כל מסע של יריבו יניח מטבע בדיוק ממול.
שימו לב שהשחקן השני אינו יכול לנקוט את אסטרטגיית המראה, בגלל מסע הפתיחה המיוחד שעשה השחקן הראשון: להצבת מטבע באמצע אין מענה סימטרי. המקום "מול" המרכז הוא המרכז עצמו, כך שהמסע הסימטרי הוא להציב מטבע שוב במרכז, וזה אינו צעד חוקי, בגלל איסור החפיפה של מטבעות. שימו לב גם לכך שצורת השולחן אינה חייבת להיות עיגול. אותה אסטרטגיה עובדת גם למלבן, ולכל צורה שיש לה סימטריה ביחס לנקודה מסוימת בתוכה.
בעיית דִידוֹ
לרועה ניתן חבל, ונאמר לו שהוא רשאי לגדר בעזרתו תחום כרצונו.
איזו צורה כדאי לו לבחור, כדי לגדור שטח גדול ככל האפשר?
שמה של הבעיה הזאת הוא "הבעיה האיזופרימטרית" ("איזופרימטרי" פירושו "שווה היקף"). בלשון מתמטית אפשר לנסח אותה כך: בין כל הצורות בעלות היקף נתון, מהי הצורה בעלת השטח הגדול ביותר? כינוי מקובל אחר לבעיה הוא "בעיית דִידוֹ", על שם מלכת קרתגו הראשונה. אחיה של דידו, שהיה מלכה העריץ של העיר צור, הרג את בעלה העשיר בגלל בצע כסף, ורצה לרשת גם אותה. דידו נמלטה באוניה, ועם כמה חברים ירדה אל החוף בטוניסיה של היום. היא שילמה למקומיים סכום כסף, שתמורתו הבטיחו לה שטח אדמה. ההסכם היה שהיא תוכל לקבל שטח שאותו תצליח לגדור בעזרת עור של שור אחד. דידו חתכה את עור השור לרצועות, וחיברה אותן לחבל. בעזרת החבל הייתה רשאית לגדור תחום, שצד אחד שלו הוא חוף הים. השאלה היא – מהי צורת התחום שהיה עליה לבחור? דידו בחרה בתשובה הנכונה – חצי עיגול. זהו "חצי" מבעיית הרועה שבה פתחנו. הפתרון לבעייתו של הרועה, כפי שלא קשה לנחש, היא הצורה בעלת הסימטריה הרבה ביותר, כלומר עיגול.
בהמשך ננסה להסביר מדוע זה כך. אבל לפני כן, כדאי להסתכל בבעיה פשוטה יותר. נניח שהרועה רוצה לבנות מכלאה לא בצורה כללית, אלא בצורת מלבן. כמובן, אפשר לבחור את המלבן בדרכים רבות – למשל מלבן גבוה מאוד וצר מאוד, או מלבן רחב מאוד ונמוך מאוד. באיזה מלבן כדאי לו לבחור? אם נביא את עניין ה"צר מאוד" לידי קיצוניות, כלומר מלבן ברוחב 0, יהיה השטח 0; גם אם נביא את עניין ה"נמוך מאוד" לקיצוניות, כלומר מלבן בגובה 0, יהיה השטח 0. יש לשער על כן שהטוב ביותר הוא האמצע בין שני המקרים הקיצוניים האלה, כלומר ריבוע. ואכן, בין כל המלבנים בעלי היקף נתון, בעל השטח הגדול ביותר הוא ריבוע. כלומר, כדאי לרועה לתחום בעזרת החבל שלו ריבוע. לעובדה הזאת יש אינספור הוכחות (כבר ציינו שלטענות פשוטות יש לעתים קרובות הוכחות רבות). הנה אחת ההוכחות הפשוטות ביותר. נסמן ב-$latex L$ את הממוצע של אורכי הצלעות של המלבן, כלומר $latex L$ הוא היקף המלבן (שהוא כזכור אורך החבל) מחולק ב-4. סכום אורכי שתי צלעות סמוכות הוא חצי מהיקף המלבן, שהוא $latex 2L$. נניח שאורך אחת משתי הצלעות הסמוכות הוא $latex L+X$. מכיוון שסכום אורכי הצלעות הסמוכות הוא $latex 2L$, אורך הצלע האחרת הוא $latex L-X$ (כי $latex L+X+L-X=2L$). שטח מלבן הוא מכפלת אורכי צלעות סמוכות, ובמקרה זה הוא $latex (L+X)\cdot(L-X)$. על פי נוסחה ידועה (שמתקבלת בסך הכול מפתיחת סוגריים), $latex (L+X)\cdot(L-X)=L^2-X^2$. אבל $latex X^2$ הוא תמיד מספר חיובי, בין אם $latex X$ חיובי ובין אם הוא שלילי. לכן הביטוי $latex L^2-X^2$ אינו עולה על $latex L^2$, שהוא שטח הריבוע בעל אותו היקף (שאורך כל צלעותיו הוא $latex L$). שטח המלבן גדול יותר ככל ש-$latex X$ קטן יותר, כלומר ככל שהצלעות קרובות יותר זו לזו באורכן.
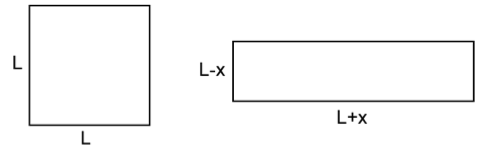
לריבוע ולמלבן שבתמונה אותו היקף, 4L. השטח של הריבוע גדול יותר.
כאן אנו מגיעים לעניין הסימטריה. נניח שהרועה נדרש עדיין לבחור תחום מלבני, אבל הוא יכול להשתמש בגְדַת נחל כאחד הגבולות של המרעה שלו, בדיוק כמו בבעייתה של דידו. כרגיל, נניח שזהו נחל מתמטי, כלומר קו ישר. מהי צורת המלבן שכדאי לו לבחור? גם כאן אפשר להשתמש בנוסחאות, אבל הפשוט ביותר הוא להשתמש בסימטריה. שקפו את התחום של הרועה ביחס לקו של גדת הנהר, הנה כך:
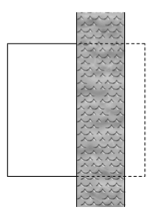
הרועה רוצה לבנות מן החבל שלו מלבן משמאל לנהר, שצלע אחת שלו היא הנהר. שיקוף המלבן הזה (הקו המקווקו) נותן מלבן בעל היקף שהוא פעמיים אורך החבל ושטח שהוא פעמיים שטח המלבן המקורי. מבין כל המלבנים שהיקפם פעמיים אורך החבל, בעל השטח הגדול ביותר הוא ריבוע. לכן כדאי לרועה לבחור במלבן שהוא חצי ריבוע.
צירוף המלבן המקורי עם המלבן המשוקף הוא תחום מלבני שאינו נעזר בנחל. כל היקפו הוא "חבל" (אף כי בחלקו חבל דמיוני), שהיקפו כפול מאורך החבל שבידי הרועה. אם כן, היקפו נתון וקבוע, ולכן כפי שאנו כבר יודעים שטחו הוא מקסימלי אם הוא ריבוע. מכיוון ששטח המלבן המקורי של הרועה הוא חצי משטח המלבן הכולל, כדאי לרועה לבחור חצי ריבוע. במילים אחרות, אורך הצלעות האופקיות של המלבן שיבחר צריך להיות מחצית מאורכה של הצלע האנכית.
חזרה לדידו ולבעיה האיזופרימטרית
בבעיה המקורית, ה"איזופרימטרית", אין מגבילים את הרועה בבחירת צורת המרעה, והוא יכול לבחור צורה כלשהי. כבר סיפרנו שכדאי לו אז לבחור בתחום מעגלי. הטענה הזאת נקראת "אי השוויון האיזופרימטרי":
בין כל התחומים בעלי היקף נתון, בעל השטח הגדול ביותר הוא עיגול.
למשפט הזה יש גם נוסח תלת ממדי, גם הוא טבעי אבל קשה יותר להוכחה: מבין כל הגופים בעלי שטח פנים נתון, הכדור הוא בעל הנפח הגדול ביותר. זוהי אחת הסיבות לכך שראשם של יונקים הוא בעל צורה כדורית למדי. מדוע האדם אינו מנצל זאת, ובונה יותר מבנים כדוריים? בין השאר, משום שכדורים אינם נארזים היטב. הרבה יותר קל לארוז מלבנים ותיבות, ומשום כך למשל חדרים בבתים סטנדרטיים הם בעלי זוויות ישרות.
אבל בואו נחזור למקרה הדו ממדי. קל לנחש שהמעגל הוא הצורה האופטימלית, עניין אחר הוא להוכיח זאת. בעוד שאת המשפט ניחשו כבר היוונים הקדמונים, הוכחה מדויקת (כמעט) ניתנה רק באמצע המאה ה-19, על ידי השוויצרי יעקב שטיינר (Jacob Steiner, 1796-1863), בן זמנו של גאוס. שטיינר היה אוטודידקט, והעיד על עצמו ששנא נוסחאות (הן "מסתירות את החשיבה", לטענתו), ואהב גיאומטריה. שטיינר השתמש ברעיון הסימטריה, בכיוון ההפוך מזה שהשתמשנו בו קודם לכן. בעוד שבמקרה של המלבן הסקנו מן השלם על חציו, הפעם נסיק מן החלק על השלם. כלומר, כמו הצייר בסיפור, נפתור "חצי בעיה", ונסיק ממנה על הכול. כמו בסיפור של דידו, נאמר לרועה שהוא רשאי לגַדֵר בעזרת החבל שלו (שאורכו קבוע) תחום שצד אחד שלו יהיה גדת הנחל. כאמור, כדאי לו (כמו לדידו) לבחור חצי עיגול. כדי להראות זאת נניח שהרועה הצליח לגדר בעזרת החבל שלו והישר $latex L$ תחום בעל שטח מקסימלי. תהיינה $latex A$ ו-$latex B$ נקודות הנגיעה של החבל ב-$latex L$. (ראו איור). תהא $latex X$ נקודה כלשהי על החבל. אנו נראה את הדבר הבא: הזווית $latex AXB$ חייבת להיות בת 90 מעלות.
אם החבל גודר שטח מקסימלי עם הישר $latex L$, אז כל נקודה $latex X$ על החבל "רואה" את הקטע $latex AB$ בזווית ישרה.
טענה זו נובעת מן הטענה הבאה:
בין כל המשולשים שיש להם שתי צלעות באורכים נתונים $latex a$ ו-$latex b$, המשולש בעל השטח המקסימלי הוא כזה שבו שתי הצלעות האלה ניצבות.
הסיבה: כאשר הצלעות ניצבות, שטח המשולש הוא מחצית מכפלת אורכיהן, כלומר $latex \frac{1}{2}ab$. שטח משולש כלשהו שאורכי צלעותיו הם $latex a$ ו-$latex b$ הוא $latex \frac{1}{2}ah$, כאשר $latex h$ הוא הגובה ל-$latex a$. הגובה $latex h$ אינו עולה על $latex b$, משום שהוא ניצב במשולש ישר זווית שהיתר שלו הוא $latex b$ (ראה איור). לכן שטח המשולש, $latex \frac{1}{2}ah$, אינו עולה על $latex \frac{1}{2}ab$.
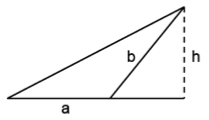
שטח המשולש שצלעותיו $latex a$ ו-$latex b$ הוא $latex \frac{1}{2}ah$, ומכיוון ש-$latex b$ גדול או שווה ל-$latex h$, שטח המשולש אינו עולה על $latex \frac{1}{2}ab$.
נניח עתה שיש נקודה X על העקום, שעבורה הזווית $latex AXB$ אינה ישרה (כלומר אינה בת 90 מעלות). נשנה את העקום, על ידי שנשנה את הזווית הזאת ל-90 מעלות, בלי לשנות את שתי הקשתות על $latex AX$ ועל $latex BX$, בהתאמה (ראה איור). על פי הטענה, השטח גדל – בניגוד להנחה שהעקום גודר עם $latex L$ שטח מקסימלי.
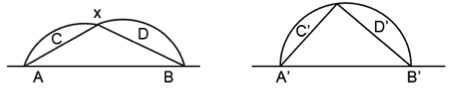
הציור הימני מתקבל מן השמאלי על ידי סגירת המִפְתַח בין הצלעות $latex XA$ ו-$latex XB$, כך שהזווית ביניהן הופכת לישרה. ה"כיפות" $latex C$ ו-$latex D$ נשמרות. אורך העקום (ה"חבל") אינו משתנה בכך. השטח, לעומת זאת, גדל, משום ששטח המשולש גדל, בעוד ששטח שתי הכיפות נשאר כשהיה.
כל שנותר הוא להשתמש במשפט פשוט מן הגיאומטריה התיכונית: אוסף הנקודות X ה"רואות" קטע $latex AB$ בזווית ישרה (כלומר שהזווית $latex AXB$ היא ישרה) הוא מעגל שקוטרו $latex AB$. בנוסח מעט שונה: אוסף הנקודות מצד אחד של הישר שרואות את $latex AB$ בזווית ישרה הוא חצי מעגל שמרכזו באמצע הקטע $latex AB$. צירופם של המשפט הזה והעובדה שגילינו נותן את מה שרצינו להוכיח: השטח שיגדור הרועה על שפת הנחל הוא חצי עיגול.
עתה נחזור אל הבעיה השלמה, של הרועה המקורי, שאין לו נחל אשר יכול לשמש כחלק מגבול התחום שלו. כדי להראות שכדאי לו לגדור בעזרת החבל שלו תחום מעגלי, נניח שהוא בחר בתחום בעל צורה אחרת. ניקח שתי נקודות על החבל, $latex A$ ו-$latex B$, שמחלקות את החבל (שיוצר צורה סגורה) לשני חלקים שווים (ראה איור שמאלי להלן).
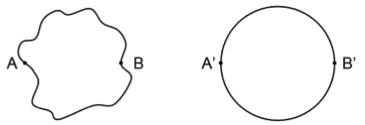
לשתי הצורות אותו היקף. העיגול שמימין מתקבל על ידי החלפת החלקים העליון והתחתון (שניהם בין $latex A$ ו-$latex B$) בצורה השמאלית בחצאי עיגולים (תוך שינוי אפשרי של המרחק בין $latex A$ ו-$latex B$). על פי מה שהוכחנו לעיל, הדבר מגדיל את השטח, ולכן לעיגול שטח גדול יותר מאשר לצורה השמאלית. זהו "אי השוויון האיזופרימטרי".
על פי האמור לעיל, כדאי לרועה להחליף גם את החלק התחתון וגם את החלק העליון של התחום שבחר בחצי עיגול. אבל פירוש הדבר הוא שכדאי לו להחליף את התחום שלו בעיגול. זהו בדיוק מה שרצינו להוכיח.
סימטריה בשירה
אָדָם זָקֵן – מַה יֵּשׁ לוֹ בְּחַיָּיו?
הוּא קָם בַּבֹּקֶר, וּבֹקֶר בּוֹ לֹא קָם.
(“ערב פתאומי”, דויד אבידן, מתוך “שירי לחץ”)
אלה הן שורותיו הפותחות של שיר זיקנה נוגע ללב שנכתב בידי צעיר בן 28. דויד אבידן, ה"ילד הנורא" של השירה העברית, נולד ב-1934. כשמת ב-1996, גלמוד וחסר כל, קשה היה לא להיזכר בשיר הזה. הבאתי אותו כאן בגלל השורה השנייה, הבנויה במתכונת של "הצלבה": המילים "קם בבוקר" מצטלבות, כדי לקבל "בוקר (לא) קם בו". ההצלבה כה נפוצה בשירה, עד כי זכתה למונח אקדמי – "כיאַסְמוּס". מקור השם באות היוונית "חִי", בעלת צורת $latex X$, מקבילת ה"חית" העברית. בדוגמה הזאת הולכת ההצלבה בכיוון מן החוץ פנימה, מבוקר בחוץ לבוקר (שאיננו) בפנים. אותו מהלך שב ומופיע בהמשך השיר:
הוּא מְדַשְׁדֵּשׁ אֶל הַמִּטְבָּח, וְשָׁם
הַמַּיִם הַפּוֹשְׁרִים יַזְכִּירוּ לוֹ,
שֶׁבְּגִילוֹ, שֶׁבְּגִילוֹ, שֶׁבְּגִילוֹ
אָדָם זָקֵן – מַה יֵּשׁ לוֹ בִּבְקָרָיו?
הוּא קָם בְּבֹקֶר קַיִץ, וּכְבָר סְתָו
נִמְהָל בָּעֶרֶב בְּנוּרוֹת חַדְרוֹ. […]
שוב, החוץ משתקף בִּפְנים: המים הפושרים מזכירים לזקן את דמו הפושר ואת חייו הפושרים. ובשורה האחרונה יש שיקוף על דרך הניגוד, משום שבמראה משתקף ההפך, סתיו במקום קיץ.
גם בשיר הבא, "האסופי" של אלתרמן, המציאות הפנימית היא תמונת ראי של המציאות החיצונית. במציאות החיצונית האם נטשה את תינוקה; האמת הפנימית שלה היא שהוא נטש אותה. לאורך השיר הפער בין התמונה לבין השתקפותה במראה גדל והולך. לסימטריית התפקידים מצטרפת סימטריה זמנית – הסוף, מותה של האם, הוא תמונת ראי של ההתחלה, לידתו של הבן, ותכריכיה הם תמונת ראי של בגדי התינוק שלו. מתוך השיר הארוך אצטט רק שלושה בתים:
הִנִּיחַתְנִי אִמִּי לְרַגְלֵי הַגָּדֵר,
קְמוּט פָּנִים וְשׁוֹקֵט, עַל גַּב.
וָאַבִּיט בָּהּ מִלְּמַטָּה, כְּמוֹ מִן הַבְּאֵר,
עַד נֻסָּה כְּהַנָּס מִן הַקְּרָב.
וָאַבִּיט בָּהּ מִלְּמַטָּה, כְּמוֹ מִן הַבְּאֵר
וְיָרֵחַ עָלֵינוּ הוּרַם כְּמוֹ נֵר. […]
הִיא זָקְנָה בְּכִלְאִי וַתִּדַּל וַתִּקְטַן
וּפָנֶיהָ קֻמְּטוּ כְּפָנַי.
אָז יָדַי הַקְּטַנּוֹת הִלְבִּישׁוּהָ לָבָן
כְּמוֹ אֵם אֶת הַיֶּלֶד הַחַי.
אָז יָדַי הַקְּטַנּוֹת הִלְבִּישׁוּהָ לָבָן
וָאֶשָּׂא אוֹתָהּ בְּלִי לְהַגִּיד לָהּ לְאָן.
וָאָנִיחַ אוֹתָהּ לְרַגְלֵי הַגָּדֵר
צוֹפִיָּה וְשׁוֹקֶטֶת, עַל גַּב.
וַתַּבִּיט בִּי שׂוֹחֶקֶת, כְּמוֹ מִן הַבְּאֵר,
וַנֵּדַע כִּי סִיַּמְנוּ הַקְּרָב.
וַתַּבִּיט בִּי שׂוֹחֶקֶת כְּמוֹ מִן הַבְּאֵר.
וְיָרֵחַ עָלֵינוּ הוּרַם כְּמוֹ נֵר.
("האסופי", נתן אלתרמן, מתוך "עיר היונה")
המספרים האלגבריים
י. לויצקי
א. דוגמאות והגדרות
המספר הרציונלי $latex \frac{3}{4}$ מקיים את המשוואה הקוית $latex x-\frac{3}{4}=0$; המספר הממשי האי-רציונלי $latex \sqrt{2}$ מקיים את המשוואה הריבועית $latex x^2 - 2 = 0$; המספר $latex \frac{\sqrt{5}}{2}$ שאף הוא אי רציונלי, מקיים את המשוואה מן המעלה הששית $latex 64x^6 -5 = 0$. קל להוכיח כי המשוואה מן המעלה השלישית $latex x^3 -3x^2+3x-3=0$ מתקיימת בשביל המספר $latex \sqrt[3]{2}+1$. המספר המדוגמה $latex \sqrt[4]{-3}$ מקיים את המשוואה הריבועית $latex x^4+3=0$ וכו׳.
הצד השווה שבכל המשוואות הנ״ל הוא כי מקדמיהן הם מספרים רציונליים. אפשר גם להניח מראש - מבלי להגביל על ידי כך את הכלליות כי בכל משוואה כזאת מקדם החזקה העליונה של $latex x$ שווה ל-$latex 1$. כך למשל במקום להסתכל במשוואה $latex 64x^6-5=0$, יכולנו לעבור על ידי חלוק המתקדמים ב-$latex 64$ למשוואה $latex x^6 - \frac{5}{64}=0$, אשר אינה שונה מן הקודמת מבחינה עקרונית.
הגדרה: מספר המקיים משוואה שצורתה
$latex \displaystyle (1) \quad x^n + a_{n-1}x^{n-1} + \ldots + a_1x + a_0 = 0$
$latex a_{n-1}, \ldots, a_1, a_0 \quad ; \quad n \gt 1$ רציונליים
נקרא בשם מספר אלגברי. מספר שאינו אלגברי נקרא מספר טרנסצנדנטי. מספר המקיים משוואה נקרא גם שורש של אותה משוואה.
מספר טרנסצנדנטי אינו איפוא שורש של שום משוואה שצורתה $latex (1)$. כל מספר רציונלי $latex a$ הוא גם אלגברי, כי הרי הוא מקיים את המשוואה $latex x-a=0$ שהיא מטפוס המשוואה $latex (1)$. המספר $latex e$ (בסיס הלוגריתמים הטבעיים), המספר $latex \pi$ (היקף מעגל שקוטרו שווה ליחידה), וכן המספר $latex 2^{\sqrt{2}}$ הם דוגמאות למספרים טרנסצנדנטיים.
הוכחותיהן של שלש עובדות אלו אינן קלות כל עיקר. את הראשונה מצא המתמטיקן הצרפתי ש. ארמיט בשנת 1873; את השניה ־ המתמטיקן הגרמני פ. לינדמן בשנת 1882; ואת השלישית - המתמטיקן היהודי א. גלפונד בשנת 1934.
כל מספר אלגברי $latex a$ הוא שרשן המשותף של משוואות רבות לאין סוף מן הטפוס $latex (1)$. כך, למשל המספר $latex \sqrt{2}$ הוא שרשן של המשוואות $latex x^2 -2 =0$ ; $latex x^3-2x=0$ וכוי.
משפט והגדרה
כל מספר אלגברי $latex \alpha$ מקיים משוואה אחת ויחידה מטפוס $latex (1)$ אשר מעלתה מזערית (קטנה ביותר). משוואה זו נקראת המשוואה המינימלית של $latex \alpha$, ולמעלתה קוראים בשם המעלה של המספר $latex \alpha$.
להוכחת משפט זה נעיר כי עצם קיומה של משוואה מינימלית הוא דבר מובן מעצמו (למה?). עיקרו של הענין הוא להראות כי קיימת רק משוואת אחת כזאת. נניח איפוא כי המספר $latex \alpha$, שמעלתו $latex n$, מקיימת שתי משוואות שונות
$latex \displaystyle (2) \quad x^n + a_1 x^{n-1} + a_2 x^{n-2} + \ldots + a_{n-1} x + a_n = 0$
$latex \displaystyle \quad \quad x^n + b_1 x^{n-1} + b_2 x^{n-2} + \ldots + b_{n-1} x + b_n = 0$
ע״י חיסור אנו מקבלים
$latex \displaystyle (3) \quad (a_1 - b_1)x^{n-1} + (a_2 - b_2)x^{n-2} + \ldots + (a_{n-1} - b_{n-1})x + (a_n - b_n) = 0$
ישנן שתי אפשרויות:
1) כל $latex a_i$ שווה ל-$latex b_i$ המתאים ($latex i=1,2,\ldots,n$), במקרה זה שתי המשוואות ב-$latex (2)$ זהות, בניגוד להנחה.
2) ישנו לפחות ערך אחד של $latex i$ כך ש- $latex a_i \neq b_i$. במקרה זה הרי $latex \alpha$ מקיים את המשוואה $latex (3)$ שמעלתה קטנה מ-$latex n$. זה סותר את הגדרת $latex n$ כמעלת המספר $latex \alpha$.
ב. מספרים אלגבריים ובניות גאומטריות
במישור יהי נתון קטע $latex AB$. נתענין כאן בשאלה: איזו קטעים אפשר לבנות על ידי הקטע $latex AB$ בעזרת הסרגל והמחוגה? דוגמות לקטעים כאלה הם למשל קטע $latex CD$ החופף למחציתו של $latex AB$, או לחלק השלישי של $latex AB$ וכוי. נבחר את הקטע $latex AB$ כקטע היחידה ונמדוד את שאר קטעי המישור לפי יחידה זו. בסעיף זה נאמר בקצור: המספר הממשי החיובי $latex \alpha$ ניתן לבניה אם קטע $latex CD$ אשר אורכו (לפי היחידה שבחרנו) שווה ל־$latex \alpha$ ניתן לבניה על ידי הקטע $latex AB$ בעזרת הסרגל והמחוגה. כל מספר רציונלי חיובי וכל שורש רבועי מכל מספר כזה (כלומר $latex +\sqrt{r}$ באשר $latex r$ הוא מספר רציונלי) הם דוגמאות למספרים הנתנים לבניה. אין זה מקרה שבכל הדוגמות הללו המספרים הם אלגבריים, כי קיים המשפט הבא:
משפט: כל מספר הניתן לבניה הוא מספר אלגברי.
כמסקנה הגיונית מן המשפט הנ״ל נקבל:
משפט: מספר טרנסצנדנטי אינו ניתן לבניה.
יש להעיר כי אלגבריותו של מספר אינה תנאי מספיק לאפשרות בנייתו של המספר הזה, אלא תנאי הכרחי בלבד. כלומר, קיימים מספרים אלגבריים אשר בנייתם היא בלתי אפשרית. מרחיק לכת יותר מן המשפט הנ״ל הוא המשפט הבא:
משפט: כל מספר הניתן לבניה הוא מספר אלגברי שמעלתו $latex n$ היא חזקה של $latex 2$ ( כלומר $latex n = 2^m$ באשר $latex m$ מספר טבעי).
גם במשפט זה עדיין אין תנאי מספיק לאפשרות בנייתו של מספר. לא נטפל בהוכחתם של המשפטים שנסחנו בסעיף הנוכחי, ואף לא נדון כאן בשאלה: מה הוא התנאי ההכרחי והמספיק גם יחד לאפשרות בנייתם של המספרים? תפקיד הסעיף הזה הוא רק להאיר מבחינה גיאומטרית את חשיבותו של מושג המספר האלגברי. למטרה זו נביא עוד כסיום לסעיף הזה את בעית תרבוע המעגל.
בעית תרבוע המעגל אשר בה טפלו לשוא היונים העתיקים ודורות רבים שבאו אחריהם היא:
במישור נתון מעגל. בנה בעזרת סרגל ומחוגה בלבד רבוע אשר שטחו שווה לשטח המעגל. אם נבחר את רדיוס המעגל הנתון כקטע היחידה, ישווה שטחו של המעגל ל-$latex \pi$. אם נסמן ב $latex \alpha$ את אורך הצלע הרבוע, אשר שטחו שווה לשטח המעגל הנתון, נקבל את השוויון $latex a^2 = \pi$ או $latex a = \sqrt{\pi}$. על סמך משפטו של לינדמן על הטרנסצנדנטיות של $latex \pi$ נובע כי גם $latex \sqrt{\pi}$ הוא מספר טרדסצנדנטי. על סמך המשפט שנסחנו לעיל בנייתה של צלע שארכה $latex \sqrt{\pi}$ ולפיכך אף בנייתו של הרבוע המבוקש הן אפוא מן הנמנעות.
ג. משפט עזר על משוואות קויות
למשוואה הקוית $latex 3x-5y=0$ בשני הנעלמים $latex (x,y)$ יש אין סוף פתרונות רציונליים כגון $latex (\frac{5}{3},1)$; $latex (\frac{10}{3},2)$ וכו׳
אף למערכת משוואות כמו למשל,
$latex x + y = 2z = 0$
$latex 3x - y + z = 0$
יש אינסוף פתרונות רציונליים, כי נוכל לחלץ אחד המשתנים מבין שתי המשוואות ואז נישאר עם משוואה אחת בשני נעלמים. ברור שנוכל להמשיך בטיעון כזה עד כל מספר של משתנים ומכאן המשפט הבא:
משפט: למערכת של $latex n$ משוואות לינאריות הומוגניות ($latex n \gt 1$) ב-($latex n+1$) נעלמים יש אינסוף פתרונות רציונליים.
ד. תכונותיהם היסודיות של המספרים האלגבריים
בסעיף הנוכחי נטפל בשאלה: מה נוכל לומר על סכומם, הבדלם, מכפלתם ומנתם של שני מספרים אלגבריים? בכוון זה נוכיח את המשפט הבא:
המשפט היסודי: יהיו $latex \alpha$ ו-$latex \beta$ מספרים אלגבריים, אז גם $latex \alpha + \beta$; $latex \alpha - \beta$ ; $latex \alpha \beta$ (ובאם $latex \beta$ שונה מ-$latex 0$) $latex \frac{\alpha}{\beta}$ הם מספרים אלגבריים. מעלותיהם של מספרים אלה שוות לכל היותר למכפלת המעלות של $latex \alpha$ ושל $latex \beta$.
הוכחה בהוכחת המשפט נצטמצם בהנחה שמעלותיהם של $latex \alpha$ ושל $latex \beta$ שוות ל-$latex 2$. טוב יעשה הקורא אם ישתדל להתקין לעצמו בעקבות האמור להלן את ההוכחה גם לגבי מעלות גבוהות יותר (ראה גם הדרכה לתרגיל ד). את ההוכחה נבצע בשלבים אחדים.
I. יהי $latex \alpha$ מספר אלגבראי ממעלה שניה. אז בשביל כל מספר טבעי $latex n$ קיימים שני מספרים רציונליים $latex r$ ו-$latex s$ כך ש-
$latex \alpha ^ n = r + s \alpha$
נוכיח את המשפט הזה בדרך האינדוקציה. נניח כי $latex \alpha$ מקיים את המשוואה $latex \alpha ^2 + p \alpha + q = 0$. אזי קיים, עבור $latex n=2$, $latex \alpha ^ 2 = -q - p \alpha$.
אם המשפט נכון עבור איזה $latex n$ שהוא, ז.א.
$latex \displaystyle (4) \quad \alpha ^n = r + s \alpha$
אזי יהיה
$latex \displaystyle (5) \quad \alpha ^{n+1} = r \alpha + s \alpha ^ 2$
$latex \quad = r \alpha + s (-q - p \alpha)$
$latex \quad = -sq + (r - sp)\alpha$
ז.א. שיהיה נכון גם עבור $latex n+1$
מאידך עבור $latex 1$, $latex n=0$ יש לנו $latex \alpha ^ 0 = 1 + 0 \cdot \alpha$, $latex \alpha ^ 1 = 0 + 1 \cdot \alpha$
II. יהיו $latex \alpha$ ו-$latex \beta$ מספרים אלגבריים, שניהם מן המעלה השניה, אז לכל ״מכפלת חזקות״$latex \alpha ^ n \beta ^ m$ ($latex n$ ו-$latex m$ מספרים טבעיים) אפשר למצוא $latex 4$ מספרים רציונליים $latex h, g, f, e$ כך ש
$latex \displaystyle (6) \quad \alpha ^ n \beta ^ m = e + f \alpha + g \beta + h \alpha \beta$
ואמנם על סמך I נוכל לכתוב $latex \alpha ^ n = r + s \alpha$ ו-$latex \beta ^ m = p + q \beta$, כאשר $latex q, p, s, r$ הם מספרים רציונליים מתאימים. על ידי הכפלה נקבל את השויון
$latex \displaystyle (7) \quad \alpha ^ n \beta ^ m = pr + ps \alpha + qr \beta + qs \alpha \beta$
אשר אם נציב בו $latex e = pr$; $latex f = ps$; $latex g = qr$; $latex h = qs$, יתן לנו את השויון $latex (6)$.
III. יהיו $latex \alpha$ ו-$latex \beta$ מספרים אלגבריים, שניהם מן המעלה השניה. אז לכל מספר טבעי $latex n$ אפשר למצוא $latex 4$ מספרים רציונליים $latex h', g', f', e'$ כך ש
$latex \displaystyle (8) \quad (\alpha + \beta) ^ n = e' + f' \alpha + g' \beta + h' \beta$
על סמך נוסחת הבינום נקבל תחילה
$latex \displaystyle (\alpha + \beta) ^ n = \alpha ^ n + \binom{n}{1} \alpha^{n-1} \beta + \ldots + \beta ^ n$
בשביל כל אחד מן המחוברים $latex \binom{n}{i} \alpha^{n-i} \beta^{i}$ בסכום הזה קיימת על סמך II הצגה מן הטיפוס הדרוש. לפיכך יהיה זה נכון גם לגבי סכומם, מש״ל.
IV. המשפט III קיים כמובן גם לגבי חזקות ההבדל $latex (\alpha - \beta)^n$
V. יהיו $latex \alpha$ ו-$latex \beta$ מספרים אלגבריים שמעלתם היא $latex 2$. נסמן ב-$latex \gamma$ את אחד המספרים $latex \alpha + \beta$, $latex \alpha - \beta$, $latex \alpha \beta$. אזי $latex \gamma$ מקיים משוואה אלגברית שמעלתה שווה לכל היותר ל-$latex 4$. על סמך II, III, IV נוכל לכתוב:
$latex \displaystyle (9) \quad 1 = \gamma ^ 0 = e_0 + f_0 \alpha + g_0 \beta + h_0 \alpha \beta$
$latex \displaystyle \quad \gamma = e_1 + f_1 \alpha + g_1 \beta + h_1 \alpha \beta$
$latex \displaystyle \quad \gamma ^ 2 = e_2 + f_2 \alpha + g_2 \beta + h_2 \alpha \beta$
$latex \displaystyle \quad \gamma ^ 3 = e_3 + f_3 \alpha + g_3 \beta + h_3 \alpha \beta$
$latex \displaystyle \quad \gamma ^ 4 = e_4 + f_4 \alpha + g_4 \beta + h_4 \alpha \beta$
כאשר המקדמים הם מספרים רציונליים. עכשיו נחפש חמישה מספרים רציונליים $latex a_0$, $latex a_1$, $latex a_2$, $latex a_3$, $latex a_4$, אשר לא כלם ישוו ל-$latex 0$, ואשר יקיימו את השוויון
$latex \displaystyle (10) \quad a_0 + a_1 \gamma + a_2 \gamma ^ 2 + a_3 \gamma ^ 3 + a_4 \gamma ^ 4 = 0$
אם נמצאם, תושלם הוכחת V. לשם כך נסתכל בארבע המשוואות ההומוגניות
$latex \displaystyle (11) \quad e_0 a_0 + e_1 a_1 + e_2 a_2 + e_3 a_3 + e_4 a_4 = 0$
$latex \displaystyle \quad f_0 a_0 + f_1 a_1 + f_2 a_2 + f_3 a_3 + f_4 a_4 = 0$
$latex \displaystyle \quad g_0 a_0 + g_1 a_1 + g_2 a_2 + g_3 a_3 + g_4 a_4 = 0$
$latex \displaystyle \quad h_0 a_0 + h_1 a_1 + h_2 a_2 + h_3 a_3 + h_4 a_4 = 0$
אשר בהן ישמשו $latex a_0, a_1, a_2, a_3, a_4$ כנעלמים.
על סמך משפט העזר ג יש פתרונות רציונליים רבים לאין סוף המקיימים את המשוואות $latex (9)$. ברור (מדוע?) שכל פתרון כזה יקיים את השוויון $latex (10)$, מש״ל.
VI. לסיום הוכחת המשפט היסודי עלינו עוד להראות: אם $latex \alpha$ ו-$latex \beta$ הם מספרים אלגבריים שמעלתם שווה ל-$latex 2$, אזי המנה $latex \alpha / \beta$ היא מספרי אלגברי שמעלתו אינה גבוהה מ-$latex 4$. להוכחת עובדה זו, תהי $latex x^2 + b_1 x + b_0 = 0$ המשוואה המינימלית של $latex \beta$, כלומר:
$latex \beta ^ 2 + b_1 \beta + b_0 = 0$
על ידי חלוק ב-$latex \beta ^ 2$ נקבל $latex 1+b_1 \frac{1}{\beta} + b_0 \frac{1}{\beta ^2}=0$ או במלים אחרות המספר $latex \frac{1}{\beta}$ מקיים את המשוואה
$latex b_0 x ^ 2 + b x + 1 = 0$
ולפיכך הוא מספר אלגברי אשר מעלתו אינה עולה על $latex 2$. לו היתה מעלתו שווה ל-$latex 1$ כי אז היה נובע כי גם מעלת $latex \beta$ היא $latex 1$ (הוכח!) בנגוד להנחה. מעלת $latex \frac{1}{\beta}$ היא איפוא בדיוק $latex 2$. על סמך V נובע עתה כי המספר $latex \alpha \frac{1}{\beta}$ כלומר $latex \frac{\alpha}{\beta}$ הוא אלגברי ומעלתו אינה עולה על $latex 4$, מש״ל.
ה. שדות מספרים
בשם שדה-מספרים, או בקצור שדה, קוראים לכל תחום של מספרים המכיל עם כל שנים ממספריו גם את סכומם, הבדלם, מכפלתם ומנתם. על סמך האמור ב-ד, תחום המספרים האלגבריים הוא איפוא שדה. דוגמות אחרות הן: שדה המספרים הרציונליים, שדה המספרים הממשיים ושדה המספרים המרוכבים. חוץ מאלה יש עוד אין סוף שדות מספרים אחרים אשר ללימודם מוקדש חלק חשוב של האלגברה הגבוהה. שדה המספרים המרוכבים הוא כמובן הרחב בין כל השדות כי הרי בו נכללים כל המספרים. לעומתו מצטיין שדה המספרים הרציונליים דוקא בתכונת ה״מינימום״: הוא מוכל כשדה חלקי בכל שדה אחר. נסה למצוא הוכחה לעובדה זו! כדי לקבל מושג ברור על היקפו של שדה המספרים האלגבריים, אנו חייבים לענות על שאלה המתעוררת מיד עם הגדרת מושג המספר האלגברי והיא: האם לכל משוואה מטפוס $latex (1)$ קיימים מספרים המקיימים אותה? התשובה לשאלה זו היא חיובית, ונובעת כמסקנה ממשפט הידועה בשם המשפט היסודי של האלגברה, אשר הוכח תחילה ע״י המתמטיקן גאוס (1855-1777). משפט זה טוען כי קיימים שרשים לכל משוואה מטיפוס $latex (1)$,יהיו מקדמי המספרים אשר יהיו. אשר למספר השרשים השונים של משוואה כזאת, הרי הוא אינו עולה על מעלת המשוואה.
נסתכל עתה במשוואה מטפוס $latex (1)$ אשר מקדמיה הם מספרים אלגבריים רצוניים (למשל: $latex x^4 - \sqrt{2} x^3 + 4 \sqrt{-75} x^2 + 3 = 0$). היתכן כי למשוואה כזו יהיו שרשים טרנסצנדנטיים? התשובה היא שלילית, כלומר קיים המשפט הבא:
משפט: אם מספר $latex \alpha$ מקיים משוואה מטפוס $latex (1)$ אשר מקדמיה הם מספרים אלגבריים, אך לא כלם רציונליים, אזי מקיים המספר הזה גם משוואה מטפוס $latex (1)$ אשר מקדמיה כלם מספרים רציונליים.
לא נטפל כאן בהוכחת המשפט הנ״ל, אם כי ההוכחה אפשרית בעזרת האמצעים אשר פתחנו ב-ד, אלא נסתפק בהערות אחדות אשר בעזרתן תתבלט חשיבותו של המשפט הזה.
שדה מספרים ייקרא סגור באופן אלגברי (בקצור: סגור אלגברית) אם שרשי כל משוואה מטפוס $latex (1)$ אשר מקדמיה לקוחים מן השדה הזה, שייכים אף הם לשדה הנדון. אי אפשר איפוא ״לצאת״ משדה זה או להרחיבו ע״י פתירת משוואות אשר מקדמיהן נמצאים בתוכו. על סמך המשפט הנ״ל נובע, כי שדה המספרים האלגבריים הוא סגור אלגברית.
לעומתו, שדה המספרים הרציונליים אינו סגור אלגברית, כי למשל למשוואה $latex x^2 - 2 = 0$ מקדמים רציונליים, אבל שרשיה הם אי-רציונליים. כן גם שדה המספרים הממשיים אינו סגור אלגברית, כי הרי מקדמי המשוואה $latex x^2+1=0$ הם ממשיים, אך שרשיה מדומים. חוץ משדה המספרים האלגבריים יש עוד שדות רבים לאין סוף הסגורים אלגברית. בין אלה מצטיין שדה המספרים האלגבריים בתכונת המינימום: כל שדה מספרים הסגור אלגברית מכיל את שדה המספרים האלגבריים.
נסיים בכמה תרגילים, אשר אולי ירצה הקוראה לנסות בהם את כוחו.
א) הוכח כי מעלת המספר האלגברי $latex \sqrt[3]{2}$ שווה ל-$latex 3$. הכלל תרגיל זה.
ב) חשב את משוואותיהם של המספרים האלגבריים $latex \sqrt[3]{2} + 1$ ו-$latex \sqrt[3]{2} + \sqrt[3]{5}$.
ג) הוכח כי המספר $latex \sqrt{2} + \sqrt{3}$ הוא אלגברי ומצא את משוואתו המינימלית.
ד) הוכח את המשפט היסודי ב-ד בשביל המקרה שמעלות המספרים $latex \alpha$ ו-$latex \beta$ הן $latex 3$ ו-$latex 2$. רמז: אם מעלת $latex \alpha$ היא $latex 3$ תתקיים במקום הנוסחה $latex (3)$ שצורתה: $latex \alpha ^ n = r + s \alpha + t \alpha ^ 2$ במקום הנוסחה $latex (6)$ יש להוכיח: $latex \alpha ^ m \beta ^ n = e + f \alpha + g \beta + h \alpha \beta + k \alpha ^ 2 + \ell \alpha ^ 2 \beta$ וכו׳.
ה) יהי $latex \alpha$ מספר אלגברי. הוכח כי מעלת $latex \alpha ^ m$ בשביל כל $latex m$ טבעי שווה לכל היותר למעלת $latex \alpha$.
ו) אם $latex r$ מספר רציונלי ו-$latex \alpha$ מספר אלגברי רצוני, אז מעלת $latex \alpha + r$ שווה למעלת $latex \alpha$.
ז) הוכח כי תחום המספרים הטרנסצנדנטיים הוא אין סופי. האם תחום זה הוא שדה?
ח) הוכח כי תחום כל המספרים שצורתם $latex r + s \sqrt{2}$, באשר $latex r$ ו-$latex s$ הם רציונליים, הוא שדה. הוא הדין לגבי תחום המספרים $latex r+ s \sqrt[3]{2} + t \sqrt[3]{4}$ ($latex t, s, r$ רציונליים).
על בעיות אחדות בגיאומטריה אלמנטרית
פ. ארדש, פורסם: מאי 1962
במאמר זה על גיאומטריה אלמנטרית נטפל במספר בעיות פתורות ונזכיר בעיות פתוחות אחדות. אני מקווה לשכנע את הקורא כי גם בגיאומטריה אלמנטרית, מקצוע בו עוסקים זה אלפי שנים, אפשר עדיין למצוא בעיות רבות חדשות הניתנות לפתרון באמצעים פשוטים למדי.
ב-1933 כשקראתי את ספרם של $latex {Hilbert ^1 , Cohn-Vossen}$ $latex {"Geometry ~and ~Imagination"}$
התעוררה אצלי הבעיה הבאה: בהנתן $latex {n}$ נקודות במישור, לא כולן על ישר אחד, האם קיים תמיד ישר העובר דרך שתיים מהן בדיוק?
למרות שהדבר נראה פשוט ביותר לא הצלחתי להתירו. ספרתי על הבעיה למתמטיקאי ההונגרי T. Gallai שמצא פתרון נאה לבעיה.
בשנת 1936 בקונגרס המתמטי באוסלו הוזכרה בעיה זו ע"י המתמטיקאי היוגוסלבי Karamatar. הוא מצא משפט זה מנוסח ללא הוכחה בספר מכניקה ישן והתקשה להוכיחו בעצמו. ב-1943 פרסמתי שאלה זו במדור השאלות של American Math. Monthly ונתקבלו פתרונות שונים. היפה שביניהם הוא פתרונו של המתמטיקאי האמריקאי
A. Kelly הנתון להלן:
נניח כי קיים סידור מישורי של $latex {n}$ נקודות, לא כולן על ישר אחד, ובכל זאת אין אף ישר אחד העובר בדיוק דרך שתי נקודות, כלומר כל ישר העובר דרך שתי נקודות חייב להכיל גם נקודה שלישית. נתבונן באוסף הישרים המוגדרים ע״י כל $latex {n}$ הנקודות ובמרחקים של כל אחת מהנקודות אל אחד מהישרים. בקבוצת מרחקים זו קיים בהכרח מרחק מינימלי $latex {d}$ המתקבל למשל בין הנקודה $latex {A}$ והישר $latex {\ell}$ מסוימים (ראה ציור מס' 1). ישר $latex {\ell}$ הוא אחד מהישרים המחברים נקודות, לכן נמצאות עליו לפי ההנחה לפחות שלש נקודות. לא ייתכן כי שתיים מהן תמצאנה מצדו האחד של עקב האנך $latex {AA'}$ על $latex {\ell}$, שכן אם $latex {B}$ ו-$latex {C}$ הן במצב כזה נעביר את הישר $latex {AB}$ והאנך $latex {CC'}$ קטן מ- $latex {AA'=d}$ בנגוד להנחתנו כי $latex {d}$ הוא הקטן במרחקים בין נקודה לישר בקבוצת הנקודות והישרים שלנו.
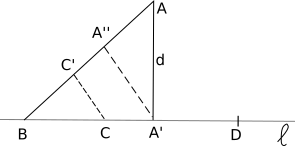
באותו אופן לא ייתכן כי תמצאנה שתי נקודות מצדו השני של העקב. האפשרות הנותרת היא כי נקודה אחת תתלכד עם הנקודה $latex {A'}$ ושתי הנקודות האחרות תמצאנה משתי צידיה. אך גם אז עדיין $latex {A'A"<d}$ בנגוד למינימליות של $latex {d}$.
קבלנו סתירה להנחתנו וזה אומר שהישר בעל המרחק המינימלי עובר דרך שתי נקודות משני צידי העקב, ורק דרכן.
Kelly הצביע גם על מקור השאלה. ב-1893 פרסם אותה המתמטיקאי היהודי Sylvester (המיסד של עתון מתמטי אמריקאי ראשון) ב-_Educational Times_ (שאלה 11851 כרך 59 עמ׳ 98) אך לא נתקבל כל פתרון, וגם לא ידוע, אם סילבסטר ידע את הפתרון. משפט זה ידוע, איפוא, בשם משפט גאלאי.
נציין שהוכחת Kelly הופיעה גם בעבודתו של Coxeter ב-American Math. Monthly (כרך 55 עמ׳ 28-26).
ב-1949 הכרתי את המתמטיקאי הישראלי מוצקין העובד כעת בארה"ב. התברר שהוא נתקל בשאלה זו ב-1933 והמתמטיקאי א. רובינזון (כעת פרופסור באוניברסיטה העברית) מצא פתרונה ב-1939.
בעקבות בעיה זו מתעוררות שאלות נוספות כגון: תהינה נתונות $latex {n>2}$ נקודות במישור, לא כלן על ישר אחד. ישר נקרא ישר רגיל כאשר הוא עובר דרך שתי נקודות בדיוק. לפי משפט גאלאי קיים לפחות ישר רגיל אחד. אפשר גם לתאר מצב כללי ביותר בו אף שלש נקודות אינן נמצאות על ישר אחד ואז יהיה מספר הישרים הרגילים $latex {\binom{n}{2} = \frac{n(n-1)}{2}}$. אם תמצאנא $latex {n-1}$ נקודות על ישר אחד והאחרונה מחוצה לו קיימים בדיוק $latex {n-1}$ ישרים רגילים.
נסמן ב- $latex {f(n)}$ את המספר המינימלי של ישרים רגילים שאפשר לקבל בסידור כל שהוא של $latex {n}$ נקודות. המתמטיקאי ההולנדי de Bruijn ואני שערנו כי $latex f(n) \to \infty$ כאשר $latex {n \to \infty}$. כלומר לכל $latex {A}$ גדול כרצוננו אפשר למצא מספר $latex {n_0}$ כך שלכל $latex {n}$ נקודות במישור שלא כלן נמצאות על ישר אחד ושמספרן גדול מ-$latex {n_0}$ (ז.א $latex {n>n_0}$) מספר הישרים הרגילים מקיים $latex {f(n)>A}$.
המתמטיקאי האנגלי G. Dirac הראה כי $latex {f(n) \geq 3}$. עבור $latex {n=3}$ ו-$latex {n=7}$ מקבלים שויון: $latex {f(n)=3}$ (עבור $latex {n=7}$ השוה את הציור מס' 2 בו הקוים הרגילים צוינו במקווקו).
מוצקין הוכיח כי $latex {f(n)>\sqrt{n}}$ ובזה אימת את השערתנו. לאחרונה הצליחו Kelly ו-Moser להוכיח כי $latex {f(n) \geq \frac{3}{7}n}$. גם כאן מתקיים שויון עבור $latex {n=7}$. יתכן שאפשר לשפר תוצאה זו ל-$latex {n}$ גדולים יותר. קיימת, למשל, ההשערה כי קיים $latex {n_0}$ כזה שעבור כל $latex {n>n_0}$ מתקיים $latex {f(n)=n-1}$. Dirac שיער שעבור $latex {n>7}$ קיים $latex {f(n) > \frac{n}{2}}$.
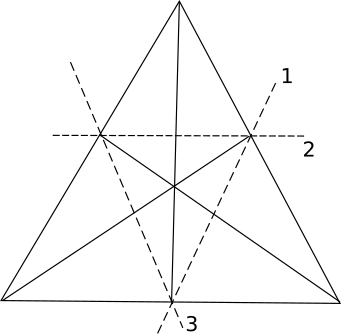
בשנת 1933 הבחנתי כי ממשפט גאלאי נובעת גם התוצאה הבאה: $latex {n}$ נקודות במישור, שלא כלן נמצאות על ישר אחד, מגדירות לפחות $latex {n}$ ישרים. (אין לשפר תוצאה זו כפי שאפשר לראות מן המקרה כאשר $latex {n-1}$ נקודות נמצאות על ישר אחד). שערתי גם שקיים $latex {n_0}$ (גדול למדי) שכל $latex {n}$ נקודות במישור עם $latex {n>n0}$ ומסודרות כך שאף $latex {n-1}$ מהן אינן על ישר אחד, מגדירות לפחות $latex {2n-4}$ ישרים.
עבור $latex {n=7}$ אין עדיין ההשערה נכונה כיון שבציור מס' $latex {2}$ אפשר לספור רק $latex {9}$ ישרים בשעה ש- $latex {2n-4=10}$ במקרה זה.
Kelly ו-Moser הוכיחו בעבודתם המוזכרת (ראה בסוף המאמר רשימה הספרות) את המשפט הכללי הבא:
נניח ש- $latex {n}$ נקודות במישור מסודרות כך, שאין יותר מ- $latex {n-k}$ מהן נמצאות על ישר אחד וש-
$latex \displaystyle (1) \quad { n \geq \frac{1}{2} [ 3 (3k-2)^2 + 3k - 1 ] }$
אזי מספר הישרים שהן מגדירות הוא לפחות
$latex \displaystyle (2) \quad {kn-\frac{1}{2}(3k+2)(k-1)}$
בטוי זה הוא ההערכה הטובה ביותר כפי שאפשר להיוכח בעזרת הדוגמה הכללית הבאה שנתנה ע"י המחברים:
תסודרנה $latex {k}$ נקודות במישור כך שאין שלש מהן על ישר אחד. נסמן ב- $latex {\ell}$ ישר רצוני שאינו עובר דרך אף אחת מהן. נעביר את כל הישרים המחברים את $latex {k}$ הנקודות ונגדיר $latex {\binom{k}{2}}$ נקודות נוספות כנקודות החיתוך של $latex {\binom{k}{2}}$ ישרים אלה עם הישר $latex {\ell}$. אליהן נצרף עוד $latex {n-k-\binom{k}{2}}$ נקודות רצוניות על $latex {\ell}$. בסך הכל יש לנו $latex {n}$ נקודות, מהן לכל היותר $latex {n-k}$ נמצאות על ישר אחד (במקרה שלנו על $latex {\ell}$). $latex {n}$ הנקודות מגדירות
$latex {1+k(n-k)-\binom{k}{2} = kn -\frac{1}{2}(3k+2)(k-1)}$
ישרים.
אם נציב $latex {k=2}$ נקבל כי עבור $latex {n \geq \frac{1}{2} [ 3 (6-2)^2 + 3 \cdot 2-1 ] = 26\frac{1}{2}}$ מספר הישרים הוא לפחות $latex {2n-\frac{1}{2}(3 \cdot 2+2)(2-1)=2n-4}$ ז.א השערתי מתקימת עבור $latex {n \geq 27}$.
יתר על כן Kelly ו-Moser הוכיחו כי השערתי נכונה גם עבור $latex {n=10}$ והם סבורים כי היא מתקיימת גם עבור $latex {11 \leq n \leq 26}$.
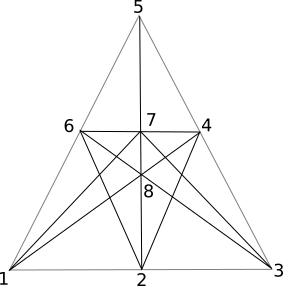
במקרים $latex {n=7,8,9}$ מקבלים לפחות $latex {2n-5}$ ישרים. זו גם התוצאה הטובה ביותר כפי שאפשר לראות עבור $latex {n=7}$ מציור מס' $latex {2}$ עבור $latex {n=8}$ מציור מס' $latex {3}$ ועבור $latex {n=9}$ מציור מס' $latex {4}$.
התוצאות של Kelly ו-Moser עדיין אינן ממצות את מכלול הבעיות הקשורות לנושא זה.
מועלית למשל ההשערה הבאה: קיים מספר קבוע $latex {C}$ שאינו תלוי ב-$latex {n}$ וב-$latex {k}$, כך ש-$latex {n}$ נקודות במישור, שלכל היותר $latex {n-k}$ מהן נמצאות על ישר אחד, מגדירות לפחות $latex {Cnk}$ ישרים. (נראה שהשערה זו נכונה עבור $latex {C=\frac{1}{10}}$).
או השערתו של Dirac: בהינתן $latex {n}$ נקודות במישור, לא כלן על ישר אחד, קיימת ביניהן נקודה אחת שממנה נמתחים אל שאר הנקודות לפחות $latex {\frac{n}{2}}$ עבור $latex {n}$ זוגי ו-$latex {\frac{n-1}{2}}$ עבור $latex {n}$ אי-זוגי, ישרים שונים.
נזכיר עוד את הבעיה הבאה שהוצגה ע"י סילבסטר: נתון סידור מישורי של $latex {n}$ נקודות. מהו המספר המקסימלי של ישרים העוברים בדיוק דרך $latex {3}$ נקודות. סילבסטר הוכיח למשל שעבור $latex {n=9}$ יתכנו לכל היותר $latex {10}$ ישרים.
ננסה עתה להכליל בעיות גיאומטריות - מישוריות אלה לבעיות קומבינטוריות.
ינתנו $latex {n}$ אלמנטים $latex {a_1, a_2, \ldots, a_n}$ ו-$latex {m}$ קבוצות חלקיות, $latex {A_1, A_2, \ldots, A_m}$ המורכבות מהם כך שכל אחת מכילה לפחות שני אלמנטים. נתנה שכל זוג אלמנטים $latex {a_i, a_j}$ מופיע ב-$latex {A_k}$ אחד ובאחד בלבד.

כדוגמה למערכת כזו ישמשו הנקודות במישור והישרים המחברים אותן בהם דנו בבעיות הקודמות.
אך קיימות מערכות מסוג זה שאינן נתנות לממוש ע"י נקודות וישרים במישור, למשל, עבור $latex {n=m=7}$, מקבלים את המערכת
$latex \displaystyle \begin{matrix} a_1 & a_2 & a_3 \\ a_1 & a_5 & a_6 \\ a_1 & a_4 & a_7 \\ a_2 & a_4 & a_6 \\ a_2 & a_5 & a_7 \\ a_3 & a_4 & a_5 \\ a_3 & a_6 & a_7 \end{matrix} $
מערכת זו המקיימת את הדרישות הנ"ל אינה ניתנת למימוש במישור כי אין פה אף ישר רגיל בנגוד למשפט גאלאי.
כאן קיים המשפט הבא:
אם $latex {m>1}$, הרי $latex {m \geq n}$.
אם נמשיך לכנות אלמנטים מוכללים אלה בשם נקודות וקבוצות חלקיות שלהם בשם קוים, נוכל לנסח את המשפט בצורה הבאה:
בסידור בו אין כל הנקודות על קו אחד מספר הקוים אינו קטן ממספר הנקודות.
זוהי הרחבה מהותית של המשפט המישורי הטוען כי $latex {n}$ נקודות שאינן על ישר אחד מגדירות לפחות $latex {n}$ ישרים.
משפט זה הוכח לראשונה ב-1938 ע"י המתמטיקאי ח. חנני (כעת פרופסור בטכניון) ובאופן בלתי תלוי ב-1941 ע"י המתמטיקאי היהודי מהונגריה Szekeres.
ההוכחה הפשוטה ביותר של עובדה זו שייכת ל- de Bruijn והיא תובא להלן:
כל שתי נקודות $latex {a_i}_1$ ו-$latex {a_i}_2$ מגדירות קו יחיד $latex {A_i}$ שהוא הקבוצה המכילה אותן (קיימת רק אחת כזו).
ב-$latex {k_i}$ נסמן את מספר הקוים העוברים דרך $latex {a_i}$ וב-$latex {s_j}$ את מספר הנקודות הנמצאות על $latex {A_j}$. ברור כי $latex {1 < k_i < n}$ וכן $latex {1 < s_j < n}$ (לא כל הנקודות הן על קו אחד ועל כל קו יש לפחות שתי נקודות).
לא קשה להוכיח כי
$latex (3) \quad \displaystyle \sum_{j=1}^n s_j = \sum_{i=1}^n k_i$
(זה אפשר לראות בעזרת אינדוקציה לפי מספר הנקודות או ע"י חשוב ישיר).
אם אין הקו $latex {A_j}$ עובר דרך הנקודה $latex {a_i}$ חייב להתקיים
$latex (4) \quad \displaystyle {s_j \leq k_i}$
כיוון שאת הנקודה $latex {a_i}$ אפשר לקשר לפחות ב-$latex {s_j}$ קוים שונים אל הנקודות שעל הישר $latex {s_j}$.
ללא אבדן כלליות אפשר להניח ש-
$latex (5) \quad \displaystyle {\min_{1 \leq i \leq n} k_i = k_n = p}$
ושהקוים $latex {A_1, A_2, \ldots, A_p}$ עוברים כלם דרך $latex {a_n}$.
ברור כי $latex {k_n > 1}$ (לא כל הנקודות הן על קו אחד).
על כל קו כזה $latex {A_j}$ $latex {1 \leq j \leq p}$ יש נקודה נוספת פרט ל-$latex {a_n}$ ונסמנה ב-$latex {a_j}$. כיון שהקוים שונים לא תמצא $latex a_j$ על $latex A_k$ $latex j \neq k$ ולכן לפי $latex {(4)}$:
$latex (6) \quad \displaystyle {s_2 \leq k_1, s_3 \leq k_2, \ldots, s_p \leq k_{p-1}, s_1 \leq k_p}$
ולכל $latex j > p$ אין $latex A_j$ עובר דרך $latex a_n$ ובודאי
$latex (7) \quad s_j \leq k_n$
נניח, כי המשפט אינו נכון, כלומר $latex m \lt n$. נצרף יחד את $latex (6)$ ו-$latex (7)$ ונקבל:
$latex (8) \quad \displaystyle \sum_{j=1}^m s_j \leq k_1 + \ldots + k_p + (m-p)k_n < k_1 + \ldots + k_p + (n-1)k_n$
וכיון ש-$latex k_n$ היה המינימלי בין ה-$latex k$-ים הרי
$latex (9) \quad \displaystyle \sum_{j=1}^m s_j < \sum_{i=1}^n k_i$
בנגוד לשויון $latex (3)$. סתירה זו מוכיחה את משפט חנני.
עבור $latex n$ נקודות במישור שלא כלן על מעגל אחד, הוכיח מוצקין בעזרת שמוש במשפט גאלאי ושמוש באינורסיה $latex ^2$, שקיים מעגל העובר בדיוק דרך $latex 3$ נקודות מהן.
להלן הוכחתו:
תהיינה $latex p_1, p_2, \ldots, p_n$ הנקודות. נקבע את $latex p_1$ כמרכז אינורסיה המעבירה את הנקודות $latex p_2, \ldots, p_n$ לנקודות $latex q_2, \ldots, q_n$. באינורסיה מכל מעגל העובר דרך המרכז (ז.א דרך $latex p_1$ במקרה שלנו) מתקבל ישר. כיון שבתחילה לא היו כל $latex p_1, \ldots, p_n$ נקודות מונחות על מעגל אחד לא תהיינה $latex q_2, \ldots, q_n$ על ישר אחד. לפי משפט גאלאי קובעות נקודות אלה לפחות ישר אחד העובר בדיוק דרך $latex 2$ נקודות, נגיד דרך $latex q_i, q_j$. מזה נובע ש-$latex p_i, p_j$ נמצאות על מעגל, שהוא מקור הישר העובר את $latex q_i, q_j$, ועובר דרך מרכז האינורסיה ז.א דרך $latex p_1$. בזה הוכח שישנו מעגל העובר דרך שלש נקודות בדיוק ($latex p_1, p_i, p_j$).
השאלה הבאה שהוצגה כבר לפני זמן רב ועדיין לא מצאה את פתרונה נראית לא קלה:
תנתנה $latex n$ נקודות במישור, לא כלן על מעגל אחד. נתבונן באוסף כל המעגלים העוברים דרך $latex 3$ נקודות לפחות. האם נכונה ההשערה כי נקודות אלה מגדירות לפחות $latex {1+\binom{n-1}{2}}$ מעגלים שונים.
כאשר $latex n-1$ נקודות נמצאות על מעגל אחד נותנת השערה זו את המספר המדויק.
הכללה קומבינטורית של בעיה זו נתנת לנסוח הבא:
יהיו $latex a_1, a_2, \ldots, a_n$ אלמנטים (שיכונו נקודות) ו-$latex A_1, \ldots, A_n$ קבוצות חלקיות שלהם (שתכוננה מעגלים), המכילות כל אחת לפחות $latex 3$ אלמנטים, וכל שלישית נקודות נמצאת בדיוק על מעגל אחד.
השאלה היא מהו הערך המינימלי של $latex m$ (מספר המעגלים המוגדרים ע"י $latex n$ הנקודות).
במקרה של זוגות היו הפתרון הגיאומטרי והקומבינטורי זהים ונתנו $latex m_{min}=n$. במקרה זה נראה אבל שהערך המתקבל בפתרון הגיאומטרי קטן מזה של הפתרון הקומבינטורי.
חנני הוכיח כפתרון לבעיה הקומבינטורית כי לכל $latex \epsilon > 0$ קיים $latex n_0$ כך שלכל $latex n$, $latex n > n_0$ מקיים ה-$latex m$ המינימלי את אי השויון
$latex (9) \quad \displaystyle m_{min} > (1-\epsilon)n^{\frac{3}{2}} \cdot 2^{\frac{-3}{4}}$
הוכחתו עדיין לא פורסמה ולהלן נביא אותה:
ללא אבדן כלליות אפשר להניח כי $latex A_1$ מכיל $latex k$ אלמנטים מתוך ה-$latex n$ ואף $latex A_i$ אינו מכיל יותר אלמנטים.
ברור שלכל היותר קיימות $latex \binom{n}{3}$ קבוצות חלקיות שונות.
אם ניחס לכל מעגל $latex k$נקודות ונספור את מספר הקבוצות החלקיות בנות שלשה אלמנטים על כל אחד מן המעגלים לחוד, הרי ספרנו כל שלישיה אפשרית שכן כל שלישיה נמצאת על מעגל מסוים.
יתכן והפרזנו בכך שספרנו $latex k$ נקודות על כל מעגל, על כל פנים:
$latex (10) \quad \displaystyle m \binom{k}{3} \geq \binom{n}{3} $
או
$latex \displaystyle m \geq \frac{\binom{n}{3}}{\binom{k}{3}} \gt \frac{n^3}{k^3} $
(כי עבור $latex n \gt k$ קיים $latex \frac{n}{k} \lt \frac{n-1}{k-1} \lt \frac{n-2}{k-2}$)
יהיו $latex a_1, a_2, \ldots, a_k$ האלמנטים של $latex A_1$ ו-$latex e_1, e_2, \ldots, e_{\binom{k}{2}}$ $latex \binom{k}{2}$ הזוגות שאפשר ליצור מ-$latex k$ אלמנטים אלה. נתבונן בשלישיות $latex (e_i, a_j)$ כאשר $latex k+1 \leq j \leq n$, כלומר $latex a_j$ אינו ב-$latex A_1$.
כל שלישיה כזו מופיעה ב-$latex A_h$ ($latex h>1$) אחד, אך $latex A_h$ כזה אינו מכיל יותר מ-$latex k-2$ שלישיות כאלה כי אין בו יותר מ-$latex k$ אלמנטים, מהם נמצאים כבר שניים ב-$latex A_1$.
קיימות, איפוא, לפחות $latex \{\frac{n-k}{k-2}\}$ (המספר השלם הראשון שאינו קטן מ-$latex \frac{n-k}{k-2}$) קבוצות $latex A_j$ המכילות $latex e_i$ נתון.
שני $latex e_i$ שונים אינם יכולים להופיע ב-$latex A_h$ אחד (פרט ל-$latex A_1$), כי אחרת היו לאותו $latex A_h$ ול-$latex A_1$ שלשה אלמנטים משותפים. לכן מספר ה-$latex A_h$ ($latex h \neq 1$) השונים הוא לפחות $latex \binom{k}{2} \{\frac{n-k}{k-2}\}$ ומכאן נובע
$latex (11) \quad \displaystyle m \geq 1+\binom{k}{2} \{\frac{n-k}{k-2}\} \geq 1+\binom{k}{2} \frac{n-k}{k-2} \gt \frac{k(n-k)}{2}$
או לפי הערכה אחרת:
$latex (12) \quad \displaystyle m \geq 1+\binom{k}{2} \{\frac{n-k}{k-2}\} \geq 1+\binom{k}{2}$
מ-$latex (10)$, $latex (11)$ ו-$latex (12)$ נובעת התוצאה $latex (9)$ למקרים שונים של $latex k$.
כאשר $latex k \leq 2^{\frac{1}{4}}n^{\frac{1}{2}}$ מתקבל מ-$latex (10)$:
$latex \displaystyle m \gt \frac{n^3}{k^3} \geq \frac{n^3}{2^{\frac{3}{4}}n^{\frac{3}{2}}} = n^{\frac{3}{2}} \cdot 2^{-\frac{3}{4}}$
אם $latex 2^{\frac{1}{4}}n^{\frac{1}{2}} \lt k \lt \frac{n}{2}$ מתקבל מ-$latex (11)$:
$latex \displaystyle m \gt \frac{k(n-k)}{2} \gt \frac{2^{\frac{1}{4}}n^{\frac{1}{2}}(n-2^{\frac{1}{4}}n^{\frac{1}{2}})}{2} = \frac{n^{\frac{3}{2}}}{2^{\frac{3}{4}}} - \frac{n}{2^{\frac{1}{2}}} \gt (1-\epsilon)\frac{n^{\frac{3}{2}}}{2^{\frac{3}{4}}}$
ניצלנו כאן את העובדה כי בתחום זה $latex k(n-k)$ עולה מונוטונית.
אי השויון האחרון נכון החל מ-$latex n=n_0$ מסוים.
בתחום $latex k \geq \frac{n}{2}$ נשתמש ב-$latex (12)$:
$latex \displaystyle m \gt \frac{\frac{n}{2} (\frac{n}{2}-1) }{2} = \frac{n^2}{8} - \frac{n}{4} \gt (1-\epsilon) \frac{n^{\frac{3}{2}}}{2^{\frac{3}{4}}}$
אין השויון האחרון מתקיים החל מ-$latex n=n_0$ מסוים.
בסך הכל $latex (9)$ הוכח בכל המקרים.
חנני הוכיח עוד כי עבור $latex n=u^2+1$, כאשר $latex u$ היא חזקה של מספר ראשוני מתקיים
$latex \displaystyle (13) \quad m \leq u(u^2+1)$
והוא משער שבמקרה זה מתקיים שויון ממש $latex m = u(u^2+1)$. מ-$latex (9)$ ו-$latex (13)$ אפשר להוכיח בעזרת תורת המספרים האנליטית כי סדר הגודל של $latex m$ במקרה של הבעיה הקומבינטורית שוה ל-$latex n^{\frac{3}{2}}$. כלומר, לכל $latex \epsilon > 0$ קיים $latex n_0$ כזה שעבור $latex n$-ים גדולים ממנו ($latex n \gt n_0$) מתקיים:
$latex \displaystyle (14) \quad (1-\epsilon) 2^{-\frac{3}{4}}n^{\frac{3}{2}} \lt m \lt (1+\epsilon)2^{-\frac{3}{4}}n^{\frac{3}{2}}$
חלקו השמאלי של $latex (14)$ הוכח לעיל, בחלקו הימני איננו יכולים לעסוק כאן. נעיר רק שהוא נובע מהמשפט הידוע שמנת שני מספרים ראשוניים עוקבים שואפת ל-1.
שאלה זו נתנת להכללה גם לקבוצות חלקיות בנות $latex l$ אברים לפחות ($latex l \gt 3$), אבל לא נעסוק בזה במאמר זה.
ספרות:
1. Th. Motzkin, The lines and planes connceting the points of finite set.
Trans. of the Amer. Math. Soc. Vol. 70 (1951) pp. 451-464
מוצקין עשה גם הכללות של משפט גאלאי עבור מרחבים רב מימדיים.
2. L.M. Kelly and W.V.J, Moser, On the number of ordinary lines determined by n points,
Canadian Jour. of Math. Vol 10 (1958) pp. 210-219
$latex ^1$ $latex D. ~Hilbert$ (1862-1943) אחד המתמטיקאים הגדולים של התקופה האחרונה. עבד בעיקרו בגטינגן שבגרמניה.
$latex ^2$ על אינורסיה ראה "גליונות מתמטיקה" מס' $latex 1$ עמ' $latex 13$.
חידות
לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 24.9.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1–כמה פירמידות?
בונים פירמידה משוכללת שכל אחת ממקצועותיה בצבע שונה.

כמה פירמידות שונות זו מזו נתן ליצור מששת המקצועות הצבעוניים?
הערה: בחידה המקורית שהכרתי, 6 המקצועות היו באורכים שונים, התשובה היא כמובן זהה, בתנאי שמכל אחת מהתמורות ניתן לבנות פירמידה.
מהו התנאי אם ידוע ששת המקצועות הם באורכים: $latex a_1 \lt a_2 \lt a_3 \lt a_4 \lt a_5 \lt a_6$?
חידה 2–האם ניתן לכסות לוח שחמט פגום ב 31 אבני דומינו?
האם ניתן לכסות לוח שחמט שהוסרו ממנו הפינה הימנית התחתונה והשמאלית העליונה (כמתואר בציור), ב 31 אבני דומינו מלבניות שרוחבן כשל משבצת הלוח וארכן כשתי משבצות?

חידה 3– בפרוס שנת תשע"ו
ראש השנה ה'תשע"ו (=5776) בפתח. הערך המספרי של השנה הקרובה יהיה ריבוע שלם. לעומת זאת יעברו יותר מ 9 שנים עד שערכה של השנה לפי הלוח הגרגוריאני (הלועזי) תהיה ריבוע שלם (2025). החידה הפעם היא האם קרה במהלך ספירת השנים לפי שני הלוחות שבאותו תאריך גם השנה לפי הלוח העברי וגם השנה לפי הלוח הגרגוריאני היו ריבועים שלמים? האם יקרו מאורעות כאלה בעתיד? ואם כן מתי יחול הקרוב ביותר?
שתהיה לכולכם שנה טובה בריבוע!
רמזים לחידות מגיליון יולי 2015
חידה 1 – חלוקת משולש כהה זווית למשולשים חדי זווית?
יש פתרון! מחייב הוספת קדקוד בתוך המשולש, מהו מספר הצלעות המינימלי שמתחברות אליו?
חידה 2 –51 מספרים?
רשמו את כל המספרים מודולו 99 (השארית לאחר חלוקה ב 99), השתמשו בעקרון "שובך היונים".
חידה 3 – האם הנמלים יישארו על המקל?
שימו לב שאם לא נשים לב לזהות הנמלים, במפגש בין שתי נמלים התוצאה זהה אם כל נמלה הופכת את כיוונה כנשאל בחידה או שהן ממשיכות בדרכן במהירות קבועה.
פתרון החידות גיליון יוני 2015
חידה 1 – מתי יפגשו הכלבים?
יש לתת את הדעת שבשל הסימטריה של הבעיה בכל רגע נתון ארבעת הכלבים ימצאו על קדקודיו של רבוע. מאחר וכל כלב רודף אחריו כלב הנע בניצב לו, רק מהירותו של הכלב הנע לארך הצלע מקטין את ארכה (מצמצם את המרחק בין הכלבים). מהירות הכלב היא 20 קמ"ש = 5.5555 מ'\שניה כלומר יעברו 36 שניות (200/5.55555) עד שהכלבים יפגשו.
דרך אלטרנטיבית לפתרון היא לפרק את וקטור המהירות של הכלבים $latex \vec{v}$ לשניים: רכיב לכוון מרכז הרבוע $latex \vec{v_r}$, ורכיב משיקי $latex \vec{v_t}$

$latex v_r = |\vec{v_r}| = \frac{1}{\sqrt{2}}v$ מאחר והמרחק של הכלב למרכז הרבוע במצב ההתחלתי הוא $latex \boldsymbol{r_0} = \frac{200}{\sqrt{2}}$ מטרים, נקבל שהזמן $latex t$ להגעתו למרכז (שם ייפגש עם שאר הכלבים) הוא $latex t = \frac{\boldsymbol{r_0}}{\boldsymbol{v_r}} = 36$ [שניות].
מאחר ולכל מרחק נתון r מהמרכז כל הכלבים ימצאו בו באותו זמן על 4 קדקודי רבוע בגודל סופי, לא יתכן ששני מסלולים יפגשו זה עם זה שלא במרכז.
במקרה של 6 כלבים על קדקודי משושה שאורך צלעו 200 מ'.
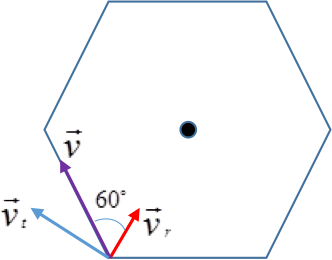
גם כאן ששת הכלבים ימצאו על קדקודי משושה שילך ויקטן. אלא שהפעם התנועה של הכלב הרודף אינה נצבת לתנועת הכלב הנרדף, הכי פשוט לפתור חידה זו בשיטה השנייה. הפעם $latex \boldsymbol{r_0} = 200$ מטרים ואילו $latex \boldsymbol{v_r} = \boldsymbol{v} \cdot \cos{60°} = \boldsymbol{v} \cdot \frac{1}{2} = 2.7777$ מטרים בשנייה. הזמן למפגש הכלבים במרכז יהיה 72 שניות.
חישוב צורת המסלול של הכלבים:
נעשה את החישוב במערכת קוארדינטות פולריות שראשיתה הוא מרכז הרבוע והזווית $latex \theta$ נמדדת ביחס לפינה השמאלית התחתונה של הרבוע.

במערכת קוארדינטות זו ניתן לרשום את שתי המשוואות לרכיבי מהירות:
$latex \displaystyle \frac{dr}{dt} = -\boldsymbol{v_r}$
$latex \displaystyle r \frac{d \theta}{dt} = \boldsymbol{v_t}$
מאינטגרציה של המשוואה הראשונה בתנאי ההתחלה: $latex r(0) = \boldsymbol{r_0}$ נקבל: $latex r = \boldsymbol{r_0} - \boldsymbol{v_r} \cdot t$
נחליף את משתנה הזמן $latex t$ במשתנה המרחק ונקבל: $latex \frac{d\theta}{dt} = \frac{d\theta}{dr} \cdot \frac{dr}{dt} = \frac{d\theta}{dr} \cdot (-\boldsymbol{v_r})$
עכשיו המשוואה השנייה תהיה (יש לתת את הדעת שבחידת 4 הכלבים $latex \boldsymbol{v_t} = \boldsymbol{v_r}$):
$latex \displaystyle \frac{d\theta}{dr} = -\frac{1}{r}$
ואחרי אינטגרציה עם תנאי ההתחלה (עבור $latex \theta=0$ $latex r=\boldsymbol{r_0}$):
$latex \displaystyle \theta = \ln{\frac{\boldsymbol{r_0}}{r}}$
זו משוואת המסלול, ובאופן גרפי:
קדקודי הרבוע האדום בשרטוט מייצגים את מיקום הכלבים לאחר כ-18 שניות.
חידה 2 – האם נתן לצבוע בשני צבעים?
נתן לצבוע בשני צבעים ההוכחה באינדוקציה. כמובן שעיגול בודד קל לצבוע, הפנים בצבע אחד והחוץ בשני. לפי הנחת האינדוקציה כל שרטוט עם $latex n$ מעגלים נתן לצבוע כנדרש. נוסיף את המעגל ה $latex n+1$, לא נשנה את צביעה מחוץ למעגל ונשנה את צבעי כל השטחים שבתוכו (זה שהיה צבוע באדום נשנה ללבן ולהפך) צביעה זו תענה לדרישות החידה, בכל השטחים שיש להם גבול משותף שהוא חלק מהמעגל ה $latex n+1$ הצד החיצוני צבוע בצבע אחד והפנימי בצבע השני (כי צבעו הוחלף) לגבי יתר הגבולות אם הם בצד החיצוני לא חל כל שינוי, ואם הם בתוך המעגל כל הצבעים הוחלפו ולכן גם כן הדרישה נשמרת.
חידה 3 – בכמה מספרים מופיעה הספרה אחד?
נבדוק קודם כל כמה מספרים בני 7 ספרות (כלומר 0-9,999,999) אינם מכילים את הספרה 1. כלומר הם בנויים מ 9 הספרות 0,2,3,4,5,6,7,8,9. מאחר ובכל אחד מ 7 המקומות יש 9 אפשריות סה"כ יש: $latex 9^7 = 4,782,969$ מספרים. שאר 5,217,031 המספרים מכילים את הספרה 1 לפחות פעם אחת. לצורך הדיוק, מאחר והחידה היא על ה תחום 1-10,000,000, מספר המספרים שמכיל 1 לפחות פעם אחת הוא 5,217,032 , לעומת 4,782,968 שאינם מכילים את הספרה 1.
בברור יש יותר מספרים המכילים את הספרה 1.
שמות הפותרים נכונה את החידות מגיליון יולי 2015
משה דוידוביץ – חידות 2 ו 3
אלעד צליק - כל החידות!