נטגר גליון 19

---

דבר העורך

אנחנו חוזרים לנושא אהוב עלינו (ונראה שגם עליכם, הקוראים) של השערות. במאמר של כותבינו הותיק, אליהו לוי, יסופר על השערות שלכל אחת מהן הוכרז פרס של מיליון דולרים.

מתוך הספר ״מתמטיקה, שירה ויופי״ מובא הפעם פרק על תחום מתמטי שנקרא ״טופולוגיה״, המדע של יריעות גומי (מממד כלשהו!).

אנחנו חוזרים ל״גליונות למתמטיקה״ הישן והטוב, ומביאים מאמר מאת מתמטיקאי שהשקיע רבות בנוער, והיה העורך של ״גליונות למתמטיקה״ - יוסף גיליס.

וכמובן - החידות של דני.

---

עוד על השערות ועל בעיות הפרס של המילניום

בגליון 16 דננו קצת בהשערות ובמעמדן במתמטיקה, והבאנו שלש השערות: (השערת רימן, השערת Birch ו Swinnerton-Dyer וההשערה ש $latex NP \neq P $) שהכרעתן תזכה את הפותר/ת באחד משבעה פרסים, כל אחד בסך מיליון דולר, שעם פרוש האלף השלישי, בשנת 2000, הציע מכון קליי (Clay Mathematics Institute), מכון פרטי במדינת מסצ'וסטס, ארה"ב, שנוסד אז למען קידום המתמטיקה, למי שיפתרו שבע בעיות מתמטיות קשות מאוד (אחת כבר נפתרה ־ ראו להלן), שהמתמטיקאים שבהם נועץ המכון ורבים אחרים רואים בין הבעיות הבולטות ביותר שהשאירה אחריה המאה העשרים. בהמשך נזכיר את שאר הבעיות.

הפרס יינתן רק כשנתיים אחרי שהפתרון פורסם, כך שהוא יוכל להיבדק ע"י הקהיליה המתמטית, כלומר ע"י המומחים המעטים שמסוגלים לכך. שכן נסיון עשרות השנים האחרונות מלמד שפתרון בעיה כזו משתרע על מאות עמודים. כך היה עם ההשג שזכה לפרסום בציבור בסוף האלף השני: הוכחת "המשפט הגדול של פרמה", (שכמובן לפני שהוכח היה ראוי לקרוא לו: ההשערה של פרמה) ־ בעיקרו של דבר זו הייתה הוכחת השערה שנקראת השערת טניימה־שימורה (Taniyama-Shimura), ע"י אנדרו ויילס (Andrew Wiles) בשנות ה־1990. לפעמים נעזרים בהוכחות כאלה עוד במחשב הבודק אלפי אפשרויות או עורך חישובי ענק, ואז למעשה רצוי לבדוק גם את התוכנה.

בניגוד למה שאפשר לחשוב, קשה להניח ששבעת מיליוני הדולרים יקדמו את פתרון הבעיות האלה, וכמו שאמר אחד המומחים ־ יותר קל לעשות מיליון דולר מאשר לפתור בעיה כזו. מי שפותר(ת) בעיה כזו צריכ(ה) להיות מראש עמוק בתוך הנושא המתמטי, ומראש בעל(ת) מוטיבציה (וכשרון) להתגבר על הקשיים והתסכולים ולחשוף את הסוד המתמטי. גם בלי פרסי המילניום הוא או היא הי(ת)ה זוכה בסיפוק ובכבוד עצומים, במשרות נחשקות ובפרסים.

לעומת זאת מה שפרסי המילניום כן השיגו, הוא לתת פרסום לשבע הבעיות, גם בין המתעניינים במתמטיקה והמתמטיקאים שאין זה שטח התמחותם ואפילו בציבור הרחב. בהקשר זה יש לשבח את בוחרי שבע הבעיות שהם בחרו בעיות מענפים שונים לגמרי במתמטיקה.

כאמור, מבין שבע הבעיות, אחת כבר נפתרה, וגם היא הייתה הוכחתה של השערה ־ הוכחת השערת פואנקרה (Poincaré) שאותה הוכיח גריגורי פרלמן מסנט־פטרבורג (רוסיה) בעקבות שיטות של ריצ'רד המילטון. אחרי שפרלמן פרסם את הוכחתו באינטרנט בשנת 2002־2003, נדרשו כשנתיים של בדיקה מאומצת ע"י מומחים כדי להשתכנע שכנראה אין בה שגיאה.

מעניין שפרלמן סרב לקבל את הפרס (שהוענק לבסוף, כתחליף, למכון פואנקרה בצרפת), וגם סרב לקבל את מדליית פילד'ס ־ הפרס היוקרתי ביותר במתמטיקה, למרות נסיונות שכנוע נמרצים. מניעיו אינם ברורים ־ הוא טוען ששופטי הפרסים אינם ראויים לשפוט את עבודתו, אבל יהי אשר יהי, הוא מציב כאן דוגמת נגד לטענה שאין בעולם דבר חשוב יותר ממיליון דולר…

השערת פואנקרה דנה בטופולוגיה של יריעות. (ראו במאמר: גיאומטריה של משטחים ומשפט Gauss-Bonnet בגליון 16.) אם בידינו בלון גמיש, נוכל לעקם אותו כך שיהיה כדורי, או מארך, או בצורת אגס. אם בידינו גלגל־ים גמיש מאוד, נוכל לעקם אותו עד שיקבל צורת ספל עם ידית! הטופולוגיה מתעלמת ממה שקורה כאשר מעקמים, ומתמקדת בהבדל בין בלון רגיל לבין גלגל־ים, וביניהם לבין בלון בצורת ביגלה עם מספר "חורים" וכו'. שטח פני בלון כזה הוא דו ממדי, והמתמטיקאים קוראים לזה "יריעה דו־ממדית". יתר על כן, היא נקראת "סגורה" כי אין לה שפה (מה שיש, למשל, לעיגול מלא, שמבחינה טופולוגית זהה לריבוע מלא).

כבר במאה התשע־עשרה, כאשר החלו לחשוב בצורה "טופולוגית" כזו, הבינו, וגם הוכיחו באופן מתמטי מדויק, שמבחינה טופולוגית יריעה דו־ממדית שהיא פני בלון כזה היא תמיד פני־כדור או פני־כדור שהוסיפו לו ידיות (גלגל ים הוא פני־כדור עם ידית אחת) ומה שקובע הוא רק מספר הידיות. במיוחד, על פני־כדור עם ידיות אפשר לשרטט עקום סגור ששום עיוות של העקום על המשטח לא יוכל לכווץ את העקום לנקודה. על בלון כדורי (או עיוות שלו) כל עקום סגור אפשר לכווץ לנקודה. ליריעה עליה כל עקום סגור ניתן לכיווץ לנקודה קוראים "פשוטת קשר".

אבל מתמטיקאים אינם נוהגים להגביל את עצמם למרחב תלת־ממדי (וגם בשימושים, כאשר יש יותר משלושה משתנים התאור הגרפי הוא מממד גדול משלוש), ובמרחב מממד ארבע, חמש, שש וכו' יהיו יריעות ממדים גבוהים יותר, ביניהן האנלוג של "פני־כדור" (למרות שקשה מאוד, או אי אפשר, "לראות" אותן באופן הסתכלותי). פואנקרה, בתחילת המאה העשרים, שיער שכל יריעה סגורה תלת־ממדית פשוטת קשר היא מבחינה טופולוגית פני־כדור תלת־ממדיים (שהם פני ה"כדור" של מרחב ארבע־ממדי!). במשך המאה העשרים הוכיחו השערות דומות ליריעות מכל ממד פרט לשלוש$latex ^1$, ובכלל מצאו שקל יותר לעבוד עם יריעות מממדים גבוהים מאשר עם התלת־ והארבע־ ממדיות. ממד שלוש חיכה לעבודתו של פרלמן.

יריעות תלת־ממדיות הן מעין מקרה ביניים: ממד שלוש נותן מצד אחד עושר שאין בממד שנים, ומצד שני אין בו חופש פראי שיש בממדים גבוהים, כך שבממד שלוש אפשר לקבל תוצאות מעניינות. למעשה, פרלמן הוכיח את השערת פואנקרה כמקרה פרטי של הוכחת השערת הגאומטריזציה של ת'רסטון (Thurston), שמכניסה סדר מופלא ביריעות התלת־ממדיות, וכשמה כן היא ־ היא מקשרת את הטופולוגיה לסוגים של גאומטריה (היפרבולית לא־אוקלידית) שבה, בניגוד לטופולוגיה, חשובים מרחקים, זויות וכו'. (ראו במאמר: גיאומטריה של משטחים ומשפט Gauss-Bonnet בגליון 16.) גם הוכחתו של פרלמן בעקבות רעיונותיו של המילטון עוברת דרך גאומטריה, משוואות דיפרנציאליות חלקיות, דברים המזכירים פיסיקה של היקום ־ הם לוקחים את היריעה = בלון (הרב־ממדית) הנתונה להם ונותנים לגאומטריה להשתנות מתוך עצמה לפי מרשם מסוים מתוך תקוה שכל ה"בליטות" ייעלמו ויתקבלו פני־כדור מושלם ־ כל זאת בלי שהטופולוגיה תשתנה. השגו של פרלמן היה בהתגברות על הקשיים הטכניים העצומים שבדרך.

כדאי לציין שגם השערת טניימה־שימורה שהביאה להוכחת המשפט הגדול של פרמה, גם השערת הגאומטריזציה של ת'רסטון, וגם בעית מילניום אחרת ־ להוכיח את השערת הודג' (Hodge), השערה שאותה יקשה עלינו לתאר כאן, הן השערות שמקבלות חשיבות מיוחדת בכך ש(אם הן נכונות), הן מכניסות סדר בתחום משמעותי מסויים, ע"י כך שהן קובעות ששני כיווני מחקר, לפעמים שונים לגמרי, נותנים תוצאות מתלכדות. נוסיף עוד שהשערת הודג' קשורה לעבודותיהם של פייר דליניה (Deligne) ופיליפ גריפית'ס (Griffiths) שיחד עם דייויד ממפורד (Mumford) זכו ב־2008 בפרס וולף המוענק בישראל.

במאמר בגליון 16 ובמאמר זה הזכרנו עד עתה חמש בעיות מילניום ־ כולן מבקשות להוכיח השערות (שאחת כבר נפתרה ע"י פרלמן). שתי בעיות המילניום הנותרות קשורות באופן הדוק לעולם הממשי ־ לפיסיקה.

נתבונן בנוזל, שנניח שהוא לא דחיס. אנו יכולים לכתוב את חוקי המכניקה היסודייים ־ חוקי ניוטון ואת תנאי האי־דחיסות. כותבים אותם בשפה של החשבון הדיפרנציאלי ומקבלים את משוואות Navier-Stokes, שהן משוואות דיפרנציאליות חלקיות. כמו בדרך כלל עם משוואות דיפרנציאליות חלקיות, באופן עקרוני די בהן, ובידיעת מצב הנוזל ברגע ההתחלה, כדי למצוא את התנהגות הנוזל בהמשך. למשל אפשר לפתור אותן במחשב בעזרת תוכנות לפתירת משוואות כאלה, ולקבל תאור גרפי ואנימציה של הנוזל. כמובן שפתרון כזה במחשב מתבסס על קירובים ־ פתרון נומרי, וכמובן שאי אפשר לבדוק במחשב את כל תנאי ההתחלה האפשריים.

למרות שמבחינה פיסיקלית ברור שהנוזל ימשיך לזרום, אין להוציא מכלל אפשרות שיש תנאי התחלה עבורם הפתרון המתמטי המדויק לא יהיה קיים לכל ערך של קואורדינטת הזמן בעתיד, מה שיראה לנו שאולי יתרחשו בנוזל תופעות הדומות, למשל, להלם על־קולי בזרימת אויר (אויר הוא דחיס, לכן המשוואות המתארות אותו קצת שונות ממשוואות נאוויר־סטוקס ואי אפשר להסיק ממנו לגביהן), או אולי תופעות קיצוניות שדורשות התחשבות בפיסיקה יותר מתקדמת, וכו'.

על סוגים רבים של משוואות דיפרנציאליות אפשר להוכיח, שאם מתקיימות הנחות טבעיות, יש להן פתרון כנדרש, הקיים עבור כל ערכי הזמן העתידיים $latex t \geq 0$ . משוואות Navier-Stokes, למרות שהתקבלו מחוקי פיסיקה יסודיים, הן כה מסובכות (לא־לינאריות) שיודעים להוכיח זאת רק לגבי נוזל במרחב דו־ממדי, ולגבי מרחב תלת־ממדי יש רק תוצאות חלקיות. בעיית המילניום מבקשת להוכיח זאת גם לגבי עולמנו התלת־ממדי, או להוכיח שההפך נכון ־ שלגבי תנאי התחלה מסוימים הפתרון "נשבר" אחרי זמן מסויים.

בעיית מילניום אחרת קשורה לפיסיקה, אבל הפעם בהקשר הבסיסי ביותר. לגבי בעיה בפיסיקה של בית־הספר עם, למשל, חוקי ניוטון, ברור שהמערכת שבבעיה, כמערכת מתמטית, קיימת. לעומת זאת הפיסיקה המודרנית מתארת כמעט הכל ע"י מה שנקרא המודל הסטנדרטי של החלקיקים האלמנטריים (קווארקים, אלקטרונים, פוטונים וכו' וכוחות הפועלים ביניהם: האלקטרומגנטי, הגרעיני החזק והגרעיני החלש), שבנוי כסוג של תורה פיסיקלית שנקרא תורת שדות קוונטית, במיוחד תורת שדות כיול. אלא שלעיתים קרובות הפיסיקאים נוהגים במתמטיקה באופנים שבמובן מתמטי שיטתי אינם תקפים. יש להם אמנם חוש בריא באילו דרכי חישוב והסק ללכת, אבל אפילו במאמצים מרובים אי אפשר להצדיק את כל מה שהם עושים ע"י הגדרות ומשפטים שכל מי שילך לפיהם יקבל תוצאות נכונות ולא סותרות זו את זו. לכן אי אפשר לטעון שהפיסיקה הבסיסית שלנו, במיוחד תורת שדות כיול קוונטית, קיימת כמערכת מתמטית.

אבל אפשר לרצות עוד פחות: לא לצאת דווקא מהדרכים המקובלות בפיסיקה, אלא לנסות להוכיח שקיים בכלל מבנה מתמטי המקיים את הדרישות הבסיסיות שהפיסיקה דורשת מתורת שדות כיול קוונטית. אפילו לכך יש הוכחות רק כאשר מפשטים את הפיסיקה או לוקחים פחות מארבעה ממדים (שלושה של חלל ואחד של זמן). הבעיה להוכיח זאת לגבי הפיסיקה כמות שהיא היא אחת מבעיות המילניום.

בעשרות השנים האחרונות התברר, להפתעת רבים, שתורות מעומקה של הפיסיקה, ביניהן תורות שדות כיול, מעניינות מבחינה מתמטית אפילו אילו לא היו חלק מהפיסיקה, למשל ככלי לפתרון בעיות מתמטיות מענפים לא צפויים. מאחר שהתורות הפיסיקליות לפעמים "לא קיימות באופן מתמטי", שימוש זה בהכרח מוגבל, ולפעמים מהווה רק "הדרכה". תפקיד זה יוגבר בהרבה אם תיפתר בעיית מילניום זו, מה שעשוי להבהיר את מקומן של תורות אלה כחלק מהמתמטיקה עצמה.

ביבליוגרפיה

J. Carlson, A. Jaffe and A. Wiles, ed. The Millennium Prize Problems. Clay Mathematics Institute and American Mathematical Society, 2006.

מרכוס דו סוטוי, המוזיקה של המספרים הראשוניים, מאנגלית: אוריאל גבעון, ידיעות ספרים, 6002.

---

$latex ^1$אני מודה לפרופ' מיכאל אנטוב, מהפקולטה למתמטיקה בטכניון, על הבהרת ענין זה.

---

טופולוגיה

המתמטיקה היא מלכת המדעים,
והאריתמטיקה מלכת המתמטיקה.
(קרל פרידריך גאוס)

מהו התחום המתמטי היפה ביותר? אני משער שלו היו עורכים משאל בין המתמטיקאים הייתה האריתמטיקה, כלומר תורת המספרים, זוכה במקום הראשון. זהו התחום העתיק ביותר, משום שהוא עוסק במושג הבסיסי ביותר. יש בו פער גדול בין עומק לבין פַּשְׁטוּת שעל פני השטח. יש בו גם ריכוז גדול במיוחד של השערות שהן כה קלות לניסוח שאפילו ילד יבינן, ועם זאת הן עומדות בפני מאמצי פתרון של דורות. באשר למקום השני בתחרות היופי, אחד המתחרים הנכבדים ביותר עליו הוא נושא מודרני יותר: הטופולוגיה, תחום ששייך למתמטיקה הרציפה אבל אינו ניתן להפרדה גם מן האלגברה. ״טוֹפּוֹס״ ביוונית פירושו ״מקום״, ו״טופולוגיה״ היא אם כך ״מדע המקום״. תיאור מדויק יותר שלה הוא ״המדע של יריעות גומי״, שֶׁכֵּן היא חוקרת אותן תכונות של יריעות שנשמרות במתיחה ובעיוות. מבחינה טופולוגית, האדם זהה לבייגל עם כמה חורים (הנחיריים, מערכת העיכול); מבחינה טופולוגית, אפשר לפשוט את החולצה בלי לפשוט קודם לכן את הסוודר. ההבדל בין טופולוגיה לבין גיאומטריה הוא שבטופולוגיה אין חשיבות לכך אם קו הוא ישר או לא, ואין מודדים מרחקים בין נקודות - כאמור, לטופולוג לא אכפת אם מותחים את יריעת הגומי שלו, ומגדילים מרחקים: בעיניו שתי יריעות המתקבלות זו מזו על ידי מתיחה הן זהות.

משפט נקודת השבת

טופולוג הוא גיאומטר שקושר את ידיו מאחורי גבו. הוא אוסר על עצמו לדבר על מרחקים. בעיניו קווי ההיקף של משולש ושל מעגל הם היינו הך, משום שאפשר לקחת משולש ולעוות אותו עד שיהפוך למעגל, ולהפך. אבל אם אין מודדים מרחקים, מה נותר לומר על צורות? תכונה אחת שהטופולוגיה חוקרת היא אם יש בצורה חורים, או לא. ואם יש, כמה חורים. היא מנסה לפתח כלים להוכחה ששני גופים "שווים" מבחינה טופולוגית, כלומר אפשר להעביר את האחד לשני במתיחה, סיבוב או שיקוף.

כדוגמה למשפט טופולוגי אספר על אחד המשפטים החשובים והידועים ביותר, משפט נקודת השבת של ההולנדי בראואר (1881-1966 ,Brouwer) מ-1912. המשפט מדבר על כדור מממד כלשהו. ״כדור״ בממד כללי הוא קבוצת כל הנקודות הנמצאות במרחק לכל היותר R מנקודה מסוימת, שהיא מרכז הכדור. בממד 1 זהו קטע באורך 2R, ב־2 ממדים זהו עיגול (״עיגול״ הוא התחום המלא, כולל הפְּנִים שלו, בניגוד ל״מעגל״ שהוא רק ההיקף). ב-3 ממדים זהו כדור רגיל, כמו זה שאנחנו משחקים בו בחוף הים, וב-4 ממדים גוף שאיננו יכולים לראות בעין. כמובן, בעיני טופולוג אין זה חשוב אם הצורה היא כדור בדיוק - כל גוף שמתקבל מן הכדור על ידי עיוות כלשהו שקול מבחינתו לכדור. משפט בראור אומר שאם לוקחים גוף כזה, מעוותים אותו, מזיזים אותו ומותחים אותו - בלי לקרוע! - ואם מותירים את כולו בתוך אותו תחום שתפס במרחב קודם לכן (כלומר לאחר העיוות והמתיחה אף נקודה אינה חורגת מן המקום בחלל שתפס הגוף קודם לכן), כי אז קיימת נקודה שלא זזה. נקודה כזו נקראת ״נקודת שֶׁבֶת״, משום שהיא נותרה יושבת במקומה.

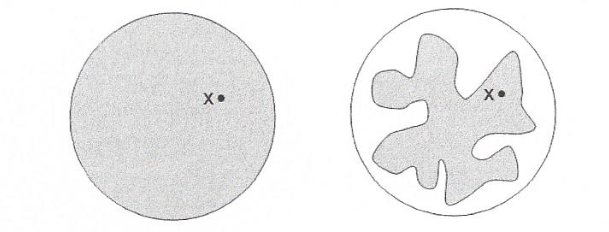
התחום האפור מימין התקבל על ידי עיוות והזזה של העיגול השמאלי, עיוות שאינו גולש אל מחוץ לעיגול. הנקודה x לא זזה - העיוות השאיר אותה במקומה. משפט בראואר אומר שבכל עיוות של העיגול שמשאיר אותו בתוך עצמו יש נקודה שנשארת במקום.

כדאי לשים לב לכך שלגבי גופים אחרים המשפט אינו נכון. קחו, למשל, עיגול והוציאו ממנו נקודה אחת - את המרכז. עתה, אם תסובבו את העיגול בזווית כלשהי שהיא גדולה מ-0 וקטנה מ-360 מעלות, לא תהיה אף נקודה שתישאר במקום. אומנם, כשהעיגול מלא, הסיבוב משאיר את המרכז במקום, אבל הן נקודת המרכז הורחקה!

את המקרה הדו ממדי של משפט בראואר אפשר להדגים בעזרת דפי נייר (אף כי נייר אפשר רק לעוות ולהזיז, לא למתוח, ולכן לא תהיה בכך הדגמה למלוא עוצמתו של המשפט). יש לזכור שבעיני טופולוג דף מלבני זהה לעיגול, משום שאפשר לקחת עיגול ולעוות אותו, מבלי לקרעו, עד שיהפוך למלבן (חישבו על יריעת פלסטלינה, ותשתכנעו שאכן כך הדבר). ובכן, קחו שני דפים מלבניים, שווי גודל ונטולי חורים, והניחו אותם זה מעל זה, כך שיחפפו בדיוק. עתה קחו את העליון מביניהם, קפלו אותו, מעכו אותו וסובבו אותו כרצונכם - אבל בלי לקרוע אותו, ובלי שנקודה כלשהי בו תחרוג מתחום הדף התחתון (התנאי האחרון פירושו שהדף העליון יישאר כולו מעל הדף התחתון). משפטו של בראוּאֶר אומר עתה שיש נקודה בדף העליון שנשארה בדיוק מעל הנקודה שמעליה הייתה קודם. כלומר, היא נשארה במקומה, מבחינת ההיטל שלה על הדף התחתון.

משפט בראוּאֶר עומד בכל הקריטריונים ליופי: ניסוחו פשוט ואלמנטרי; הוכחתו עמוקה; הוא פורה מאוד, בכך שפרץ דרך לתחום שלם בטופולוגיה; וכן, הוא שימושי מאוד, גם בתחומים מרוחקים מן הטופולוגיה. למשל, הוא מועיל להוכחת קיום פתרונות למשוואות מסובכות. בנוסף לכך, הוא מהווה דוגמה מאלפת לשילוב של תחומי מתמטיקה שונים. אף שבניסוח המשפט אין זכר לפעולות חשבוניות, כלומר לאלגברה, ההוכחה המקובלת והפשוטה ביותר שלו היא אלגברית. היא משתמשת בכלים מתחום שפותח בסוף המאה ה-19 ובתחילת המאה ה־20, שנקרא ״טופולוגיה אלגברית״. אביו של התחום הזה היה הצרפתי אנרי פואנקרה (1854-1912 ,Henri Poincaré). בפרק הבא נראה שימוש מפתיע למשפט בראוּאֶר במתמטיקה הבדידה.

משפט בּוֹרסוּק-אוּלָם

ערב מלחמת העולם השנייה הייתה בפולין פריחה מתמטית קצרה אך מרהיבה. בבתי הקפה של לבוב ושל וורשה, שני מרכזי המחקר הגדולים, פעלו חוקרים ששמותיהם ידועים כיום לכל מתמטיקאי - בַּנַך (Banach), מַזוּרקֶביץ' (Mazurkewic), קוּרטוֹבסקי (Kuratowski), טַרְסקי (Tarski), בורסוק (Borsuk), אוּלָם ורבים אחרים. במיוחד נשכרה מכך הטופולוגיה. סטניסלב אוּלָם (Stanyslaw Ulam), אחד הצעירים בחבורה, לא היה טופולוג במקצועו, אבל הוא ניסח השערה בסיסית, שהוכחה במהרה על ידי בּוֹרסוּק, והיא נקראת מאז ״משפט בורסוק-אולם״. אנסח אותו תחילה על דרך הדוגמה:

בכל רגע נתון קיימות על קו המשווה שתי נקודות
אנטיפודיות(כלומר שנמצאות בדיוק זו מול זו) שבהן נמדדת
בדיוק אותה טמפרטורה.

״קו המשווה״ הוא רק משל - אפשר לקחת במקומו כל מעגל. במקום הטמפרטורה אפשר לקחת גודל כלשהו, בתנאי שזהו גודל רציף, כלומר אין בו קפיצות. הטמפרטורה היא דוגמה לגודל רציף, משום שאינה ״קופצת״, שפירושו שאם בנקודה מסוימת נמדדת טמפרטורה של (נאמר) 10 מעלות, אז בנקודות קרובות לה הטמפרטורה תהיה קרובה ל-10 מעלות. זו הייתה דוגמה למקרה החד ממדי של משפט בּוֹרסוּק-אוּלָם. הנה דוגמה למקרה הדו ממדי:

בכל רגע נתון יש על פני כדור הארץ שתי נקודות אנטיפודיות
(כלומר שנמצאות בדיוק זו מול זו), שבהן בדיוק אותה
טמפרטורה וגם אותו אחוז לחות.

באופן כללי, מנוסח המקרה הדו ממדי של משפט בורסוק-אולם כך: אם על פניו של כדור 3 מימדי (הפָּנִים עצמם הם מממד 2) נמדדים 2 פרמטרים רציפים, אז יש שתי נקודות אנטיפודיות שבהן שני הפרמטרים שווים. המקרה ה־3 ממדי של משפט בורסוק-אולם יאמר שאם ניקח כדור 4 ממדי, שפניו הם 3 ממדיים (אל תנסו לדמות לעצמכם כדור כזה - זהו יצור מופשט!) ונמדוד על פניו 3 פרמטרים, יהיו שתי נקודות אנטיפודיות שכל אחד מן הפרמטרים יהיה שווה בשתיהן. משפט בורסוק־אולם הכללי אומר דבר דומה, בנוגע לפני כדור מממד כלשהו.

המקרים ה־2 ממדיים ואילך של המשפט הם קשים ועמוקים. המקרה ה-1 ממדי, לעומת זאת, פשוט למדי, ואוכל לתאר את ההוכחה שלו. זיכרו - המקרה ה-1 ממדי אומר שעל פני קו המשווה (שהוא פשוט דוגמה למעגל) יש שתי נקודות אנטיפודיות שבהן הטמפרטורה (שהיא פשוט דוגמה לפרמטר רציף, או בלשון המתמטיקה ״פונקציה רציפה״) שווה. לצורך ההוכחה נצייר מחוג עם ראש וזנב כמו באיור הבא:

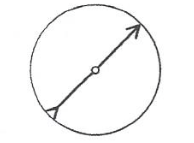
משפט בּוֹרסוּק-אוּלָם אומר שאם נסובב את המחוג על פני קו המשווה, נגיע למצב שבו בראש המחוג ובזנבו נמדדת אותה טמפרטורה. ההוכחה נעשית על ידי הסתכלות בהפרש בין הטמפרטורה בראש והטמפרטורה בזנב. אם ההפרש חיובי, אז אחרי סיבוב ב-180 מעלות הוא יתהפך, ולכן יהיה שלילי. גודל שעובר ברציפות מחיובי לשלילי חייב לעבור דרך 0, ולכן באיזושהי נקודת ביניים הוא יהיה שווה ל-0. והפרש 0 פירושו טמפרטורות שוות בשני קצות המחוג.

נציב את המחוג במצב כלשהו, ונחשב את ההפרש בין הטמפרטורה בראשו והטמפרטורה בזנבו. אם במצב שבחרנו ההפרש הזה הוא 0, פירוש הדבר הוא שהטמפרטורה בנקודות הראש והזנב שוות, ואלה הן אז שתי נקודות אנטיפודיות שבהן הטמפרטורה שווה, שהוא מה שרצינו להוכיח. נוכל להניח אפוא שההפרש הזה אינו 0. נניח, לשם דוגמה, שהטמפרטורה בראש היא 10 ובזנב 3, ואם כן ההפרש הוא $latex 10-3=7$ מעלות. נסובב עתה בדמיוננו את המחוג באופן רציף ב־180 מעלות, כלומר עד שנקודות הראש והזנב יתחלפו, וכל אותה עת נמדוד את הפרש הטמפרטורות בין הראש והזנב. כאשר נגיע למצב הסופי, כלומר נשלים סיבוב של 180 מעלות, יהיה ערך הטמפרטורה בראש החץ (היכן שקודם היה הזנב) 3 מעלות, ואילו הערך בזנב (במקום בו היה קודם הראש) הוא 10 מעלות. ההפרש בין הראש והזנב יהיה על כן $latex 3-10=-7$ מעלות. ההפרש עבר אפוא מֵעֶרך חיובי לערך שלילי. מכיוון שאנו מניחים שהטמפרטורה היא פרמטר רציף, כלומר אין בה קפיצות, הרי לפי משפט ערך הביניים שלמדנו בפרק הקודם ההפרש חייב באיזושהי נקודה להיות שווה 0. אבל כאמור הפרש טמפרטורות 0 בין ראש וזנב פירושו בדיוק שתי נקודות אנטיפודיות שבהן ערך הטמפרטורה שווה!

שימוש למתמטיקה בדידה

מי שפוגש לראשונה את משפט בּוֹרסוּק-אוּלָם עשוי לשאול את עצמו ״אז מה״. אין לי ברירה אלא לתת את דברתי שהמשפט הזה חשוב, מבחינה זו שיש לו שימושים רבים. אבל אוכל להביא ראיה אחת - שימוש של המשפט למתמטיקה בדידה. זהו אכן עניין מפתיע ביותר, משום שבבעיה שנפגוש מייד לא מוזכרת טופולוגיה בשום צורה שהיא!

הבעיה נקראת ״בעיית חלוקת המחרוזת״. שני גנבים גנבו מחרוזת (פתוחה, כלומר לא מעגלית), ששזורים בה חרוזים מסוגים שונים, כאשר מכל סוג יש מספר זוגי של חרוזים. הגנבים רוצים להתחלק בשללם באופן הוגן, שבו כל גנב יקבל אותו מספר חרוזים מכל סוג כמו חברו. לשם כך, כמובן, יצטרכו לחתוך את המחרוזת. אבל חיתוך מפחית מערכה של המחרוזת, ולכן הם מעוניינים להשתמש במספר חיתוכים קטן ככל האפשר. לכמה חיתוכים יזדקקו? המתמטיקאי הישראלי נוגה אלון השתמש במשפט בורסוק-אולם כדי להוכיח את המשפט הבא:

אפשר להסתפק במספר חיתוכים שהוא כמספר סוגי
החרוזים.

לא אֶלאה מלחזור על כך שתמיד כדאי לבדוק את הדוגמה הפשוטה ביותר. במקרה זה, המקרה הפשוט ביותר הוא שבו יש סוג אחד של חרוזים, ואכן אז אפשר להסתפק בחיתוך אחד - פשוט חותכים את המחרוזת באמצע. גם במקרה של שני סוגי חרוזים ההוכחה אינה מסובכת במיוחד. אבל מ-3 סוגי חרוזים ואילך ההוכחה היחידה המוכרת משתמשת במשפט בּוֹרסוּק-אוּלָם!

כשחותכים את המחרוזת בשתי הנקודות כמסומן, ונותנים לגנב א' את חתיכות A ו-C ולגנב ב' את חתיכה B, מתקבלת חלוקה ״הוגנת״ - כל גנב מקבל 4 חרוזים לבנים ו-3 שחורים. כאשר יש שני סוגי חרוזים, כמו בדוגמה זו, מספיקים תמיד שני חיתוכים. ל-k סוגים מספיקים k חיתוכים.

---

על החישוב של π

יוסף גיליס

כידוע נהוג להשתמש באות היוונית $latex \pi$ לסמן את היחס בין היקף של מעגל לקוטרו, בהיותה האות הראשונה של המילה היוונית περιφέρεια, שפירושה ״היקף״.

בימי קדם התקבלו בתרבויות שונות קירובים והערכות שונים לגבי ערכו של $latex \pi$, אבל ארכימדס היה הראשון שניסה באופן מדעי לחשב את ערכו המדויק. שיטתו תוארה כבר במאמר בחוברת קודמת של עתון זה (כרך 5, מסי 4) ולא נכנס כאן לפרטים. הגישה העיקרית היתה לחסום מצולעים משוכללים במעגל וגם לחסום את המעגל במצולעים כאלה. ארכימדס ידע לחשב את שטחי המצולעים האלה ומאחר ששטח המעגל גדול מזה של כל מצולע שחסום בו וקטן משטח המצולע החוסם אותו, הצליח ארכימדס לקבוע גבולות שביניהם נמצא $latex \pi$. במיוחד הוכיח כי

$latex \displaystyle 3\frac{10}{71} \lt \pi \lt 3\frac{1}{7}$

באופן עקרוני ניתן להמשיך לפי שיטתו של ארכימדס ולחשב את $latex \pi$ לכל דיוק שנרצה, אבל החישובים נעשים מסובכים מאד. חסרון שני בשיטת ארכימדס הוא שאי אפשר להסיק ממנה נוסחה מפורשת עבור $latex \pi$.

רוב המאמצים לחשב את $latex \pi$ בתקופה האחרונה התבססו על נוסחה המיוחסת למתמטיקאי הגרמני ליבניץ (G.W. Leibnitz).

הנוסחה היא:

$latex \displaystyle (1) \quad \arctan{x} = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \frac{x^9}{9} \dots$

אם $latex -1 \lt x \leq 1$, כאשר $latex \arctan{x}$ נמדד ברדיאנים. נדחה את הוכחת נוסחה זו לסוף המאמר ובינתיים נראה איך להסיק ממנה מסקנות.

אם נציב $latex x=1$, נקבל מיד כי

$latex \displaystyle \frac{\pi}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} + \dots$

אבל באיזה אין תועלת רבה. כי כדי לחשב את $latex \pi$ לפי נוסחה זו עד לדיוק של 10 ספרות, נצטרך להביא בחשבון לפחות שני מיליארד אברים של הטור. כי הרי אם נפסיק את הסיכום אחרי $latex 2N$ אברים, ז.א. באבר $latex -\frac{1}{4N-1}$, תהיה שארית הטור

$latex \displaystyle (\frac{1}{4N+1} - \frac{1}{4N+3}) + (\frac{1}{4N+5} - \frac{1}{4N+7}) + \dots$

$latex \displaystyle = \frac{2}{(4N+1)(4N+3)} + \frac{2}{(4N+5)(4N+7)} + \dots$

$latex \displaystyle \gt \frac{2}{(4N+2)^2} + \frac{2}{(4N+6)^2} + \dots$

$latex \displaystyle = \frac{1}{2} [ \frac{1}{(2N+1)^2} + \frac{1}{(2N+3)^2} + \dots ] $

$latex \displaystyle \gt \frac{1}{2} [ \frac{1}{(2N+2)^2} + \frac{1}{(2N+4)^2} + \dots ] $

$latex \displaystyle = \frac{1}{8} [ \frac{1}{(N+1)^2} + \frac{1}{(N+2)^2} + \dots ] $

וניתן להוכיח, אם כי לא נציג כאן את ההוכחה, כי הנוסחה האחרונה בסוגריים ערכה בערך $latex \frac{1}{N}$. ראינו איפוא כי אם ניקח $latex 2N$ אברים מהטור ניתקל בשגיאה של לפחות $latex \frac{1}{8N}$. כדי להשיג דיוק של 10 ספרות דרוש כי

$latex \displaystyle \frac{1}{8N} \lt 10^{-10}$

ולכן $latex N \gt 10^9$, ז.א. שידרשו, כפי שאמרנו, לפחות $latex 2 \cdot 10^9$ אברים. מאידך ידוע כי, עבור כל $latex \alpha, \beta$

$latex \displaystyle (2) \quad \tan{(\alpha + \beta)} = \frac{\tan{\alpha} + \tan{\beta}}{1 - \tan{\alpha} \tan{\beta}}$

אם נכתוב $latex \tan{\alpha} = a$, $latex \tan{\beta} = b$ ובכן $latex \alpha = \arctan{a}$, $latex \beta = \arctan{b}$ נקבל

$latex \displaystyle (3) \quad \arctan{a} + \arctan{b} = \arctan{\frac{a+b}{1-ab}}$

במיוחד, אם ניקח $latex a=\frac{1}{2}$, $latex b = \frac{1}{3}$, נקבל

$latex \displaystyle \arctan{\frac{1}{2}} + \arctan{\frac{1}{3}} = \arctan{\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{6}}} = \arctan{1} = \frac{1}{4}\pi$

מהטור של לייבניץ יוצא עכשיו:

$latex \displaystyle (4) \quad \frac{1}{4}\pi = (\frac{1}{2} - \frac{1}{3}\cdot \frac{1}{2^3} + \frac{1}{5} \cdot \frac{1}{2^5} - \frac{1}{7} \cdot \frac{1}{2^7} + \frac{1}{9} \cdot \frac{1}{2^9} \dots)$

$latex \displaystyle \quad + (\frac{1}{3} - \frac{1}{3}\cdot \frac{1}{3^3} + \frac{1}{5} \cdot \frac{1}{3^5} + \frac{1}{5} \cdot \frac{1}{3^5} - \frac{1}{7} \cdot \frac{1}{3^7} \dots)$

שני הטורים האלה הם מכשירים יעילים למדי למטרות חישוב נומרי. נניח שנסכם את $latex 2N$ האברים הראשונים של הטור הראשון. השארית תהיה

$latex \displaystyle \frac{1}{4N+1} \cdot \frac{1}{2^{4N+1}} - \frac{1}{4N+3} \cdot \frac{1}{2^{4N+3}} + \frac{1}{4N+5} \cdot \frac{1}{2^{4N+5}} \dots$

$latex \displaystyle = \frac{1}{4N+1} \cdot \frac{1}{2^{4N+1}} - [ \frac{1}{4N+3} \cdot \frac{1}{2^{4N+3}} - \frac{1}{4N+5} \cdot \frac{1}{2^{4N+5}} ] \dots$

$latex \displaystyle \lt \frac{1}{4N+1} \cdot \frac{1}{2^{4N+1}}$

$latex \displaystyle \lt \frac{1}{4N \cdot 2^{4N+1}} = \frac{1}{N \cdot 2^{4N+3}}$

נוכל איפוא לקבל דיוק של 10 ספרות אם

$latex \displaystyle N \cdot 2^{4N+3} \gt 10^{10}$

וזה יתקיים, כפי שאפשר לברר בקלות, אם $latex N \gt 7$.

יוצא כי מספיק לקחת 14 אברים מהטור הראשון (ואפילו פחות מהטור השני) להשיג דיוק של 10 ספרות. למעשה ניתן להוכיח בדרך דומה כי, באופן כללי ההפרש בין הסכום של k האברים הראשונים של הטור (1) לבין הערך המדויק של $latex \arctan{x}$, כאשר $latex -1 \lt x \lt 1$, הוא קטן מ-

$latex \displaystyle \frac{x^{2k}}{2k(1-x^2)}$

נסתכל עכשיו בנוסחה (3) ונציב $latex a = b = \frac{1}{5}$. נקבל

$latex \displaystyle 2 \arctan{\frac{1}{5}} = \arctan{\frac{\frac{1}{5}}{1-\frac{1}{25}}} = \arctan{\frac{5}{12}}$

ולכן

$latex \displaystyle 4 \arctan{\frac{1}{5}} = 2 \arctan{\frac{5}{12}} = \arctan{\frac{\frac{5}{6}}{1-\frac{25}{144}}} = \arctan{\frac{120}{119}}$

מאידך, בהסתמך שוב על (3), קיים

$latex \displaystyle \arctan{1} + \arctan{\frac{1}{239}} = \arctan{\frac{1+\frac{1}{239}}{1-\frac{1}{239}}} = \arctan{\frac{120}{119}}$

ומכאן ש-

$latex \displaystyle (5) \quad \frac{1}{4} \pi = \arctan{1} = 4 \arctan{\frac{1}{5}} - \arctan{\frac{1}{239}}$

אם נציב $latex x=\frac{1}{5}$ ב-(1) נראה, לפי האמור לעיל, שנקבל דיוק של 10 ספרות אם ניקח k אברים כך ש-

$latex \displaystyle \frac{(\frac{1}{5})^{2k}}{2k \cdot \frac{24}{25}} \lt 10^{-10}$

ולזה מספיק ש-$latex k \gt 7$. באשר לטור (1) כאשר $latex x = \frac{1}{239}$, קל לראות כי 3 אברים יספיקו. ההצבה (5) מאפשרת איפוא לחשב את $latex \pi$ בדיוק רב בעבודה קלה יחסית. בעזרת הנוסחה (4) הצליח המתמטיקאי האנגלי יוהן מצ׳ין (John Machin) כבר בשנה 1706 לחשב את $latex \pi$ עד לספרה ה-100. קיימות מספר רב של נוסחאות אלטרנטיביות, ביניהם זו של אוילר (L. Euler) משנת 1779, והיא

$latex \displaystyle (6) \quad \frac{1}{4} \pi = 5 \arctan{\frac{1}{7}} + 2 \arctan{\frac{3}{79}}$

המתמטיקאי שנקס (W. Shanks) המשיך במאמצים האלה ובשנת 1873 פרסם רשימה של 707 הספרות הראשונות בפיתוח העשרוני של $latex \pi$. עם פיתוחם של מחשבים אלקטרוניים לבשה בעית החישוב צורה חדשה. עכשיו יכול כל תלמיד תיכון היודע תכנות לחשב את $latex \pi$ עד לדיוק של מליוני ספרות תוך כמה דקות.

בהקשר זה נזכיר מקרה מבדר במקצת. בשנת 1937 התקיימה בפאריז (בירת צרפת) תערוכה גדולה ואחד הביתנים בה היה ״ביתן המדע״. לשם קישוט בבנין זה שמו על ארבעה הקירות מסביב את 707 הספרות של $latex \pi$ שהיו ידועות עד אז. הבנין קיים, על כל קישוטיו, עד ליום הזה ומשמש כ״מוזיאון המדע״. אבל לפני כשלושים שנה, כאשר התחילו להשתמש במחשבים אלקטרוניים חישבו את $latex \pi$ לדיוק של כמה אלפי ספרות ואחת העובדות שהתגלו היתה שבחישוביו של שנקס היתה כנראה טעות והספרות אחרי הספרה ה-135 אינן נכונות!

בסוף נזכיר שתי גישות אחרות לחישוב של $latex \pi$.

א. המתמטיקאי האנגלי ברונקר (Brouncker) הוכיח בשנת 1658 את הנוסחה הבאה:

$latex \displaystyle (7) \quad \frac{4}{\pi} = 1 + \cfrac{1}{2 + \cfrac{9}{2 + \cfrac{25}{2+ \cfrac{49}{2 + \cfrac{81}{2+ \cfrac{121}{2 + \dots}}}}}}$

לא נוכל להוכיח נוסחה זו כאן ואנו מצטטים אותה בעיקר מפני שהיא כל כך שונה מאלה שניתנו למעלה.

ב. הנוסחה השניה הומצאה ע״י המתמטיקאי הצרפתי ויטה (F. Vieta) שחי במאה ה-16. הוא יצא מהעובדה כי

$latex \displaystyle \sin{\alpha} = 2 \cos{\frac{\alpha}{2}} \cdot \sin{\frac{\alpha}{2}}$

$latex \displaystyle \quad = 2 \cos{\frac{\alpha}{2}} (2 \cos{\frac{\alpha}{4}} \sin{\frac{\alpha}{4}})$

$latex \displaystyle \quad = 2^2 \cos{\frac{\alpha}{2}} \cos{\frac{\alpha}{4}} \sin{\frac{\alpha}{4}}$

$latex \displaystyle \quad = 2^2 \cos{\frac{\alpha}{2}} \cos{\frac{\alpha}{4}} (2 \cos{\frac{\alpha}{8}} \sin{\frac{\alpha}{8}})$

$latex \displaystyle \quad = 2^3 \cos{\frac{\alpha}{2}} \cos{\frac{\alpha}{4}} \cos{\frac{\alpha}{8}} \sin{\frac{\alpha}{8}}, \dots$

רואים כי ניתן להמשיך בדרך זו ובאופן כללי,

$latex \displaystyle \sin{\alpha} = 2^n \cos{\frac{\alpha}{2}} \cos{\frac{\alpha}{2^2}} \cos{\frac{\alpha}{2^3}} \cdots \cos{\frac{\alpha}{2^n}} \sin{\frac{\alpha}{2^n}}$

דהיינו:

$latex \displaystyle \cos{\frac{\alpha}{2}} \cos{\frac{\alpha}{2^2}} \cos{\frac{\alpha}{2^3}} \cdots \cos{\frac{\alpha}{2^n}} = \frac{\sin{\alpha}}{2^n \sin{\frac{\alpha}{2^n}}}$

אבל ידוע כי $latex \frac{\sin{\theta}}{\theta}$ שואף לערך הגבולי 1 כאשר $latex \theta$ שואף ל-0. מכאן שכאשר $latex n$ גדל לקראת אינסוף ישאף

$latex \displaystyle 2^n \sin{\frac{\alpha}{2^n}}$

שהוא אינו אלא

$latex \displaystyle \alpha \cdot \frac{\sin{\frac{\alpha}{2^n}}}{\frac{\alpha}{2^n}}$

לערך הגבולי $latex \alpha$. מהשיקולים האלה הסיק ויטה את הנוסחה

$latex \displaystyle (8) \quad \frac{\sin{\alpha}}{\alpha} = \cos{\frac{\alpha}{2}} \cos{\frac{\alpha}{2^2}} \cos{\frac{\alpha}{2^3}} \cos{\frac{\alpha}{2^4}} \dots$

נציב ב-(8) $latex \alpha = \frac{\pi}{2}$ וניזכר כי $latex \sin{\frac{\pi}{2}} = 1$, נקבל

$latex \displaystyle (9) \quad \frac{2}{\pi} = \cos{\frac{\pi}{2^2}} \cos{\frac{\pi}{2^3}} \cos{\frac{\pi}{2^4}} \dots$

אבל, עבור כל זווית $latex \theta$, קיים

$latex \displaystyle \cos{\theta} = 2 \cos^{2}\frac{\theta}{2} - 1$

ולכן

$latex \displaystyle (10) \quad \cos{\frac{\theta}{2}} = \sqrt{\frac{1 + \cos{\theta}}{2}}$

כולנו יודעים כי

$latex \displaystyle \cos{\frac{\pi}{2^2}} = \frac{1}{\sqrt{2}} = \sqrt{\frac{2}{4}}$

ולכן, לפי (10),

$latex \displaystyle \cos{\frac{\pi}{2^3}} = \sqrt{\frac{1 + \frac{1}{\sqrt{2}}}{2}} = \sqrt{\frac{2 + \sqrt{2}}{4}}$

אם נמשיך, נקבל

$latex \displaystyle \cos{\frac{\pi}{2^4}} = \sqrt{\frac{1 + \sqrt{\frac{2+\sqrt{2}}{4}}}{2}} = \sqrt{\frac{2 + \sqrt{2 + \sqrt{2}}}{4}}$

ובאותה דרך

$latex \displaystyle \cos{\frac{\pi}{2^5}} = \sqrt{\frac{2 + \sqrt{2 + \sqrt{2 + \sqrt{2}}}}{4}}$

וכו׳.

נציב את כל אלה ב-(9) ונקבל את נוסחת ויטה

$latex \displaystyle \frac{2}{\pi} = \sqrt{\frac{2}{4} \sqrt{\frac{2 + \sqrt{2}}{4}} \sqrt{\frac{2 + \sqrt{2 + \sqrt{2}}}{4}} \cdots}$

 הוכחת הנוסחה (1)

ההוכחה הפשוטה ביותר מתבססת על חשבון אינטגרלי: נניח כי $latex 0 \lt x \lt 1$. אזי

$latex \displaystyle \arctan{x} = \int_0^x \frac{\text{d}u}{1+u^2} = \int_0^x (1 - u^2 + u^4 - u^6 + \dots) {d}u = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \dots$

ברור שהפיתוח של $latex \frac{1}{1+u^2}$ בטור הנדסי אפשרי אך ורק אם $latex u^2 \lt 1$ ולכן התנאי $latex 0 \leq x \lt 1$ היה דרוש. נוסף על זה הנחנו שהאינטגרל של סכום של טור אינסופי שווה לסכום האינטגרלים של אברי הטור. דבר זה אינו נכון תמיד אבל ניתן לאשר כי הוא קיים במקרה זה. המעבר ל-$latex x$ שלילי הוא מידי מאחר שגם $latex \arctan{x}$ וגם נוסחת ליבניץ מחליפים את סימנם כאשר מציבים $latex -x$ במקום $latex x$.

---

חידות

דניאל לובזנס

כנראה שהתחלת שנת הלימודים והחגים בעקבותיה, לא פינו לקוראי זמן לענות על החידות בגיליון ספטמבר, אשמח לקבל פתרונות, גם אחרי שפורסמו הרמזים.

לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 24.10.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.

חידה 1 –שמיכת טלאים?

שמיכת טלאים ריבועית בנויה מ 169 טלאים שכל אחד מהם ריבוע – כמתואר בציור. רוצים לחלק אותה לשתי שמיכות כל אחת גם היא ריבועית- כל אחד מהטלאים המרכיבים אותה צריך להישאר שלם (מותר לחתוך רק לאורך התפרים שבין הטלאים). איך ניתן לעשות חלוקה כזו כך שהשמיכה המקורית תחולק ל 4 חלקים בלבד?

יש להוכיח כי אי אפשר לעשות זאת בחלוקה של השמיכה המקורית לפחות מ 4 חלקים.

חידה 2–איזו ספרה חסרה?

נתון כי המספר $latex 2^{29}$ בנוי מ 9 ספרות שונות. האם ניתן למצוא איזו ספרה חסרה מבלי לחשב את ערכו של $latex 2^{29}$?

חידה 3– איזה מספרים ניתן לרשום כסכום של רצף של מספרים טבעיים?

יש מספרים שניתן לרשום כסכום של רצף של מספרים טבעיים, למשל: $latex 3+4+5+6+7=25$. לעומת זאת אי אפשר לרשום את המספר 8 כרצף כזה (הדרישה היא שברצף יהיו לפחות 2 מספרים טבעיים).

איזה מספרים ניתן לרשום כרצף של מספרים טבעיים ואיזה לא ניתן?

רמזים לחידות מגיליון ספטמבר 2015

חידה 1 –כמה פירמידות?

יש להיזהר ולא לספור שתי צורות זהות פעמיים, תנו דעתכם גם על צורות שאחת היא דמות ראי של השנייה.

חידה 2–האם ניתן לכסות לוח שחמט פגום ב 31 אבני דומינו?

שימו לב למספר המשבצות השחורות ולמספר הלבנות.

חידה 3 – בפרוס שנת תשע"ו

השתמשו בשוויון $latex a^2 - b^2 = (a+b) \cdot (a-b)$ ובכך שמדובר במספרים טבעיים.

פתרון החידות גיליון יולי 2015

חידה 1 – חלוקת משולש כהה זווית למשולשים חדי זווית?

יש פתרון! מחייב הוספת קדקוד בתוך המשולש ($latex Q$ בשרטוט למטה) שממנו נמתחים 5 קוים (בצבע אדום בשרטוט) המייצרים 5 משולשים כך שהסכום של 5 זוויות הראש שלהם הוא 360 מעלות ולכן כל אחת יכולה להיות חדה. הפתרון המפורט דורש בנייה מדויקת שתבטיח שאכן כל המשולשים יהיו חדי זווית.

אני מביא כאן את פתרונו המבריק של הקורא אלעד צליק שהצליח למצוא בנייה יפה שנותנת פתרון לחלוקת כל המשולשים כהיי הזווית האפשריים.

נתון משולש $latex ABC$ שזווית הראש שלו $latex A$ כהה.

בניה:

נשרטט מ $latex A$ את האנך $latex AJ$ ל $latex BC$ (גובה המשולש).

נעביר קו $latex D’E’$ המקביל ל$latex BC$ ($latex D’$ ו $latex E’$ נמצאות על $latex AB$ ו $latex AC$ בהתאמה) וחותך את $latex AJ$ בנקודה $latex Q$ כך ש $latex D’E’=QJ$. קיים קו כזה כי אם נזיז את $latex Q$ באפן רציף מ $latex J$ ל $latex A$ נתקדם באפן רציף מ $latex D’E’ \gt QJ$  ל $latex D’E’ \lt QJ$ ולכן איפה שהוא בדרך תהיה נקודת השוויון.

נסמן נקודה $latex K$ על $latex AJ$ הנמצאת מרחק קטן מעל לנקודה $latex Q$ (במהלך ההוכחה נמצא חסמים לארכו של הקטע $latex KQ$ שיהיה קצר אבל סופי) ונעביר דרך $latex K$ קו $latex DE$ המקביל ל $latex BC$ חותך את $latex AB$ ו $latex AC$ בנקודות $latex D$ ו $latex E$ בהתאמה.

מהנקודות $latex D$ ו $latex E$ נוריד אנכים ל $latex BC$ שיחתכו אותו בנקודות $latex F$ ו $latex G$ בהתאמה.

נעלה מ $latex D$ אנך ל $latex AB$ שיחתוך את $latex BC$ בנקודה $latex H$.

נעלה מ $latex E$ אנך ל $latex AC$ שיחתוך את $latex BC$ בנקודה $latex I$.

נבחר באפן שרירותי נקודה $latex R$ שתמצא על $latex BC$ בין $latex F$ ל $latex J$ או $latex H$ (כלומר אם $latex HF \gt FJ$ היא תהיה בין $latex F$ ל $latex J$ –כמו המקרה בשרטוט, ואילו אם $latex HF \lt FJ$ היא תהיה בין $latex F$ ל $latex H$ ).

נבחר באפן שרירותי נקודה $latex S$ שתמצא על $latex BC$ בין $latex G$ ל $latex J$ או $latex I$ (כלומר אם $latex GJ \gt GI$ היא תהיה בין $latex G$ ל $latex I$ –כמו המקרה בשרטוט, ואילו אם $latex GJ \lt GI$ היא תהיה בין $latex G$ ל $latex J$)

טענה: המשולשים $latex QAD$ $latex QAE$ $latex QSE$ $latex QRS$ $latex QDR$ $latex BDR$ ו- $latex SEC$ כולם חדי זווית ולכן מהווים פתרון לחידה.

בשרטוט הבא מופיעים 7 המשולשים כל אחד בצבע שונה:

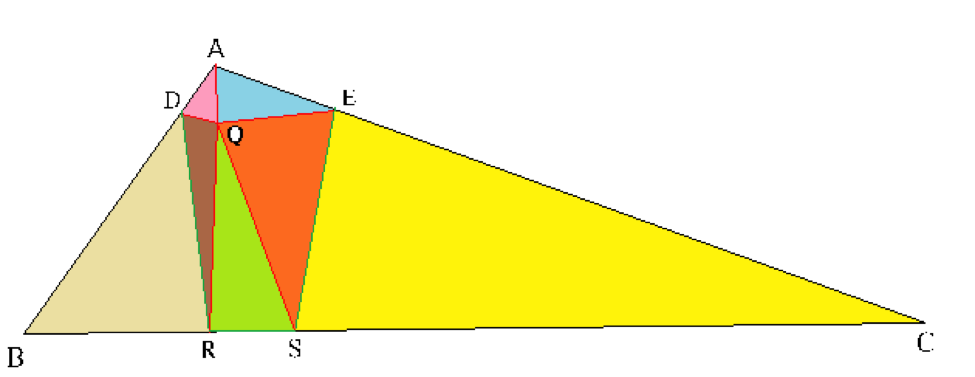
הערה: לחדי הראיה מביניכם ששמו לב לכך שבשרטוט הזווית $latex \sphericalangle DQR$ אינה חדה, זה נובע מכך שבשרטוט הקטע $latex KQ$ אינו קצר מספיק, וזה כדי שהשרטוט יהיה קריא – אם הוא היה קצר יותר, כלומר הקו $latex DE$ היה סמוך יותר ל $latex D’E’$ הזווית הזו הייתה חדה.

הוכחה: נראה לגבי כל אחד מ7 המשולשים כי כל זוויותיו חדות. בשל הסימטריה ניתן להסתפק בהוכחה מפורטת רק ל 4 משולשים.

משולש AQE:

משולש $latex AKE$ ישר זווית ולכן הזויות $latex \sphericalangle KAE$ ו-$latex \sphericalangle KEA$ חדות. כמו כן יש לתת את הדעת ש $latex \theta = \sphericalangle QEK$ היא זווית קטנה כרצוננו אבל גדולה מ-0 .

מכאן נסיק לגבי זוויות המשולש:

$latex \sphericalangle QAE = \sphericalangle KAE \lt 90°$

$latex \sphericalangle AQE = \sphericalangle AKE - \theta = 90° - \theta \lt 90°$

$latex \sphericalangle QEA = \sphericalangle KEA + \theta $ מאחר ו $latex \sphericalangle KAE$ חדה ו $latex \theta$ קטנה כרצוננו גם $latex \sphericalangle QEA$ חדה.

משולש AQD: בגלל הסימטריה הוכחה דומה לזו של משולש $latex AQE$.

משולש ECS:

$latex \sphericalangle SCE$ זווית חדה במשולש ישר זווית $latex EGC$.

$latex \sphericalangle ESC$ זווית חדה במשולש ישר זווית $latex EGS$.

$latex \sphericalangle SEC \lt \sphericalangle IEC = 90°$

משולש BDR: בגלל הסימטריה הוכחה דומה לזו של משולש $latex ECS$.

משולש QES:

$latex \sphericalangle EQS = \sphericalangle E'QS + \theta = \sphericalangle QSJ + \theta$ מאחר ו $latex \sphericalangle QSJ$ חדה (זווית חדה במשולש ישר זווית $latex QSJ$) ו $latex \theta$ קטנה כרצוננו גם $latex \sphericalangle EQS$ חדה.

$latex \sphericalangle QES = 90° - \theta - \sphericalangle SEG \lt 90°$

$latex \sphericalangle ESQ$ נמצאת מול הצלע הקצרה ביותר במשולש $latex QES$ (כי $latex DE \lt QJ$) ולכן היא קטנה משאר הזוויות שהראנו שהן חדות.

משולש DQR: בגלל הסימטריה הוכחה דומה לזו של משולש $latex QES$.

משולש QRS:

$latex \sphericalangle QSR$ זווית חדה במשולש ישר זווית $latex QSJ$.

$latex \sphericalangle QRS$ זווית חדה במשולש ישר זווית $latex QRJ$.

$latex \sphericalangle RQS$ נמצאת מול הצלע הקצרה ביותר במשולש $latex QES$ (כי $latex RS \lt FG = DE \lt D’E’ = QJ$) ולכן היא קטנה משאר הזוויות שהראנו שהן חדות.

 חידה 2 –51 מספרים?

נרשום את כל המספרים מודולו 99 (השארית לאחר חלוקה ב 99). אם שניים זהים אז ההפרש ביניהם מתחלק ב99 ולכן כולם שונים. יתכן ונמצא ביניהם המספר 0 ואז שום מספר שנחבר אליו (ושונה ממנו) לא ייתן מספר המתחלק ב-99 . נותרו 50 מספרים שונים. את 98 המספרים 1-99 נתן לחלק ל 49 קבוצות שונות שבכל אחת מהן זוג מספרים שסכומם 0 (מודולו 99 ):

(1,98)

(2,97)

(3,96)

.

.

(48,51)

(49,50)

מאחר ונותרו לנו 50 מספרים, לפחות שניים מהם יהיו שייכים לאותה קבוצה ולכן סכומם יהיה 0 מודולו 99 – כלומר סכומם יתחלק ב 99.

חידה 3 – האם הנמלים יישארו על המקל?

אם לא נשים לב לזהות הנמלים, במפגש בין שתי נמלים התוצאה זהה אם כל נמלה הופכת את כיוונה כנשאל בחידה או שהן ממשיכות בדרכן במהירות קבועה. כלומר שנמלה הנמצאת בקצה הימני של המקל תוכל ללכת לכל אורכו עד שתיפול כעבור 500 שניות. ולכן 500 שניות הוא הזמן המקסימלי שבו יישארו נמלים על המקל, כמובן שמספרן ההתחלתי של הנמלים אינו משנה…

שמות הפותרים נכונה את החידות מגיליון ספטמבר 2015

משה דוידוביץ – חידה 3.