נטגר גליון 2
דבר העורך
רון אהרוני
בגיליון הקודם הסברתי שהעיתון מיועד ל”מי שאוהב דברים כאלה”. מתברר שהרבה אנשים “אוהבים דברים כאלה” - האתר זכה לכניסות רבות.
הגיליון הנוכחי נשאר פחות או יותר באותה מתכונת:
מדור בעיות (את הבעיות שלא נפתרו מן הגיליון הקודם השארנו על כנן!)
המדור על דמויות במתמטיקה עוסק הפעם במתמטיקאי ההונגרי הגדול פאול טוראן - חברו של המתמטיקאי ההונגרי המפורסם עוד יותר, פאול ארדש.
במדור ההיסטוריה של המתמטיקה כותב פרופ’ ליאו קורי מאוניברסיטת תל אביב על דרכם הפתלתלה של המספרים המרוכבים להתקבלות כאזרחים שווי זכויות בממלכת המספרים.
במדור ההשערות כותב ד”ר יוסי כהן מן הפקולטה למתמטיקה (ואחד העורכים של העיתון הזה) על בעיה פתוחה בתורת המספרים.
שני מאמרים נוספים: מאמר של ד”ר אליהו לוי על הוכחה קצרה ויפה במיוחד לאי האפשרות לחלק זווית לשלושה חלקים בעזרת מחוגה וסרגל בלבד (מלווה בסיפור היסטורי), ומאמר של פרופ’ אורי בדר מן הטכניון על תהליך של מיצוע, שמופיע בהרבה תחומים מתמטיים.
פתחנו גם מדור חדש, שמיועד לצעירים יותר (אבל אולי גם אחרים ימצאו בו עניין). במדור הזה יש הפעם מאמר שלי, על שברים עשרוניים אינסופיים, ומדור חידות אלמנטריות (אין פירושו שהן קלות!)
בנוסף לכותבים, תודה גם לעושים במלאכה: ד”ר יוסי כהן, שבצד תפקידי עריכה הוא גם ממונה על הפקת העיתון; אסף שפירא, שממונה על מדור הבעיות; ד”ר גדי אלכסנדרוביץ’, שנזכיר שוב את האתר המתמטי שלו - $latex {http://www.gadial.net/}$. ולבסוף - תודות כפולות ומכופלות לאחראי הטכני על העיתון, אורי פרץ.
רון אהרוני,
הפקולטה למתמטיקה, הטכניון
פול טוראן
גבור הלס
הדברים שלהלן לקוחים מתוך הרצאה שנתנה ע"י Gábor Halasz במסגרת תחרות המתמטיקה הדו-לאומית ישראל-הונגריה ע"ש פרופ' יוסף גיליס ופרופ' פול טוראן. את המאמר תירגם מר אורי וייס. ערך אותו בעברית: פרופ' רון הולצמן. הכותב מניח ידיעה של מספרים מרוכבים.
פול טוראן (Paul Turán)
פול טוראן (Paul Turán) שעל שמו נקראת התחרות, היה הפרופסור שלי באוניברסיטה וראש המחלקה במכון המתמטי שבו עבדתי לאחר סיום לימודי.
אני יודע שבוודאי שמעתם עליו: נאמר לי שכולם מכירים את המשפט המפורסם שלו בתורת הגרפים (Graph Theorem). למעשה, הוא לא עבד הרבה בתורת הגרפים. פעמים רבות הוא הסתפק בלתת את התוצאה הראשונה, או להוכיח את המשפט הראשון, אשר יסדו תחום מחקר חדש ואז לתת לאחרים להרחיב את המשפטים והרעיונות שלו. בדרך זו הוא השאיר את חותמו בתחומים רבים של המתמטיקה כגון תורת המספרים, אנליזה, קומבינטוריקה, הסתברות, ואלגברה.
יוצא מן הכלל הוא מה שהיום נקרא "שיטת סכומי החזקות של טוראן". זו היא יצירתו הגדולה ביותר ואשר עליה עבד לאורך כל חייו. הוא איגד את כל התוצאות שהשיג בתחום זה בספר שניקרא "על שיטה חדשה באנליזה ושימושיה" (On a New Method of Analysis and its Applications) אשר פורסם לאחר מותו. בחלקו הראשון של הספר ניתנת התיאוריה עצמה אשר כוללת אי-שיוויונות כלליים עבור סכומים של חזקות של מספרים מרוכבים. אני מניח שאתם כבר מסוגלים לעכל את מרביתו של החלק הראשון. אתן דוגמה לסוג האי-שיוויונות שבהן עוסק הספר.
נניח שניתנים לנו מספר סופי של מספרים מרוכבים,
$latex \displaystyle z_1, z_2, \ldots, z_n $
העלו אותם בחזקת $latex {\nu}$ וסכמו אותם. התוצאה שתקבלו נקראת "סכום חזקות מיוחד". אם נרשה בנוסף מקדמים מרוכבים כל שהם, הסכום יקרא "סכום חזקות כללי":
$latex \displaystyle s_\nu \overset{\text{def}}{=} b_1z_1^\nu + \cdots + b_n z_n^\nu \quad (\nu=m+1,\ldots,m+n) $
אשר אותו נבחן עבור $latex {n}$ ערכים עוקבים של $latex {\nu}$, כאשר $latex {m\geq0}$ הוא מספר שלם נתון. טוראן התעניין בלהראות שסכומי החזקות הללו אינם יכולים להיות "קטנים מידי", במילים אחרות הוא התעניין באי-שיוויון מהסוג:
$latex \displaystyle \max_{m+1 \leq \nu \leq m+n} |s_\nu| \geq \ldots $
כאשר הצד הימני יתכן ויהיה תלוי במקדמים $latex {b_j}$, ב - $latex {m}$ וב - $latex {n}$,
אבל אינו תלוי בערכי $latex {z_1,z_2,\ldots,z_n}$ (אך אולי יתכנו אילוצים
כלליים על ערכים אלו). בדוגמא הנוכחית, בצד הימני יופיע הגורם
$latex {|s_0|=|\sum_{j=1}^n b_j|}$ אשר יהיה הגורם היחיד אשר יהיה תלוי
במקדמים ובנוסף, יהיה האילוץ הבא על המספרים המרוכבים:
$latex \displaystyle |z_j| \geq 1 \quad (j=1,\ldots,n) $
אנו מעוניינים באי-השיוויון הטוב ביותר מסוג זה או לפחות משהו קרוב
אליו.
האם מישהו יכול להסביר למה אנו דורשים טווח של $latex {n}$ חזקות או יותר?
כלומר, למה לא יתכן אי שיוויון כזה עבור סדרה של $latex {n-1}$ חזקות עוקבות?
(שהרי ע"י בחירה מתאימה של המקדמים $latex {b_j}$-פה בתפקיד הנעלמים-אנו
יכולים לדאוג שכל $latex {n-1}$ סכומי החזקות יהיו אפס וכן $latex {s_0\neq 0}$).
במקום לחפש ישירות את ה - $latex {s_\nu}$ הגדול ביותר, נשתמש בעיקרון אשר
ניקרא "עיקרון הדואליות" (duality principle). במקרה שלנו
העיקרון מבוסס על אי שיוויון פשוט
$latex \displaystyle \left| \sum_{\nu=m+1}^{m+n} c_\nu s_\nu \right| \leq \max_{m+1 \leq \nu \leq m+n} |s_\nu| \sum_{\nu=m+1}^{m+n} |c_\nu| $
אם, ע"י בחירה מתאימה של המספרים המרוכבים $latex {c_\nu}$, נוכל לגרום לצד
השמאלי להיות "גדול" ותוך כדי כך לדאוג שהצד הימני ישאר "קטן" יחסית,
אז נקבל חסם תחתון טוב למקסימום אותו אנו בוחנים.
נציב את ערכו של $latex {s_\nu}$ ע"פ ההגדרה שלו,
$latex \displaystyle \sum_{\nu=m+1}^{m+n} c_\nu s_\nu = \sum_{\nu=m+1}^{m+n} c_\nu (b_1z_1^\nu + \cdots + b_n z_n^\nu) $
בסכום הכפול (הצד הימני) נסדר מחדש את האיברים ונקבץ יחדיו את אותם
איברים אשר מכילים את אותו $latex {z_j}$:
$latex \displaystyle =\sum_{j=1}^n b_j (c_{m+1} z_j^{m+1} + \cdots + c_{m+n} z_j^{m+n}) $
אם נבחר את המקדמים $latex {c_\nu}$ כך שכל הסכומים בתוך הסוגריים יסתכמו
לאחד,
$latex \displaystyle c_{m+1} z_j^{m+1} + \cdots + c_{m+n} z_j^{m+n} = 1 \quad (j=1,\ldots,n) $
אז הסכום הכפול יסתכם ל - $latex {s_0}$.
השיוויון האחרון הוא משוואה פולינומיאלית ב - $latex {z_j}$: נקח
$latex \displaystyle P_{m+n}(z) = 1 - c_{m+1} z^{m+1} - \cdots - c_{m+n} z^{m+n}; $
פה ובהמשך, הציון התחתי של הפולינום ישמש לציון הדרגה (או חסם עליון
עליה). בסימון זה עלינו אם כך לפתור
$latex \displaystyle P_{m+n}(z_j) = 0 \quad (j=1,\ldots,n) $
אילוץ זה קל לספק: כל ה - $latex {z_j}$ הם שורשיו של פולינום מדרגה $latex {n}$
$latex \displaystyle \omega_n(z) \overset{\text{def}}{=} \left(1-\frac{z}{z_1}\right)\cdots\left(1-\frac{z}{z_n}\right) $
וכל מכפלה
$latex \displaystyle P_{m+n}(z) \overset{\text{def}}{=} \omega_n(z) Q_m(z) $
היא בעלת אותה תכונה; הפולינום $latex {Q_m}$ בעל דרגה לכל היותר $latex {m}$, כפי
שניתן ללמוד מהציון התחתי שלו, ע"מ לדאוג שדרגתו של $latex {P_{m+n}(z)}$ לא
תחרוג מ - $latex {m+n}$.
נניח כעת,
$latex \displaystyle \omega_n(z) = a_0 + \cdots + a_n z^n \; (a_0=1), \quad Q_m(z) = d_0 + \cdots + d_m z^m $
נשאר לנו לבחור את המקדמים $latex {d_0,\ldots, d_m}$. על הפולינום
$latex {P_{m+n}}$ להיות בעל צורה מיוחדת. המקדם החופשי
שלו הוא $latex {1}$:
$latex \displaystyle a_0d_0=1 \quad \rightarrow \quad d_0=1 $
וכן המקדמים עד לדרגה ה - $latex {m}$ מתאפסים:
$latex \displaystyle \begin{array}{c} a_0 d_1 + a_1 d_0 = 0 \quad \rightarrow \quad d_1=\ldots \\ a_0 d_2 + a_1 d_1 + a_2 d_0 = 0 \quad \rightarrow \quad d_2=\ldots \end{array} $
וכך הלאה. בצורה רקוסיבית ניתן לחשב את $latex {d_1,d_2,\ldots,d_m}$, שכן
$latex {a_0=1\neq0}$, על פי הידוע נכון לעכשיו (משפט חביב על
טוראן לציון עיניינים טריוויאליים).
על כן, חישבנו את $latex {c_\nu}$, אבל אנחנו עדיין לא סיימנו שכן הם תלויים
בערכים של המספרים $latex {z_j}$ ולכן עלינו למצא חסם עליון לסכום הערכים
המוחלטים שיהיה בלתי תלוי ב - $latex {z_j}$. הערכה זו היא פחות או יותר
מיידית ואני מתנצל שאינני נותן את כל הפרטים. אני משוכנע שתוכלו למלא
את הטיעונים החסרים.
למשל, תוכלו לראות בקלות שעבור $latex {P_{m+n}(z)}$ כמכפלת שני פולינומים
מתקבל
$latex \displaystyle 1+\sum_{\nu=m+1}^{m+n} |c_\nu| \leq (|a_0|+\cdots+|a_n|) (|d_0|+\cdots+|d_m|) $
עבור שני פולינומים מדרגה כלשהי, ואפילו עבור פולינומים מדרגה "אין
סופית", כלומר מה שנקרא טור חזקות,
$latex \displaystyle A(z) = \sum_{k=0}^\infty \alpha_k z^k, \quad B(z) = \sum_{k=0}^\infty \beta_k z^k $
נשתמש בסימון
$latex \displaystyle A(z) \ll B(z) $
אותו נקרא כ - "$latex {B(z)}$ שולט על $latex {A(z)}$" ומשמעו
$latex \displaystyle |\alpha_k|\leq \beta_k \quad (k=0,1,\ldots) $
בהמשך נעשה שימוש בחשבון של טורי חזקות פורמאליים (ללא צורך
בהתכנסות). אם המושג אינו מוכר לכם, תמיד תוכלו "לחתוך" את הטור
במקום סופי על מנת להצדיק את החישוב. בדרך זו, לדוגמא, קל לראות ש
$latex \displaystyle A_1(z) \ll B_1(z),\; A_2(z) \ll B_2(z) \implies A_1(z)A_2(z) \ll B_1(z)B_2(z) $
ובאינדוקציה ניתן להרחיב זאת למספר גורמים כלשהו במקום רק שניים.
נתחיל בכך שנמצא גורם השולט על $latex {\omega(z)}$. מכיוון ש $latex {|z_j|\geq1}$,
$latex \displaystyle 1-\frac{z}{z_j} \ll 1+z $
ועל פי ההערה האחרונה
$latex \displaystyle \omega_n(z) \ll (1+z)^n, \quad |a_k|\leq \binom{n}{k}, \quad |a_0|+\cdots+|a_n|\leq 2^n $
ובקשר ל - $latex {Q_m(z)}$, הגדרנו את המקדמים שלו בצורה רקורסיבית כאשר
עצרנו בשלב ה - $latex {m}$-י. אם, במקום זאת, נמשיך ברקורסיה עד אינסוף (ad
infinitum), נקבל טור חזקות
$latex \displaystyle Q(z) = \sum_{k=0}^\infty d_k z^k $
עבורו
$latex \displaystyle \omega_n(z) Q(z) = 1 $
כלומר
$latex \displaystyle \begin{array}{ll} Q(z) &= \displaystyle{\frac{1}{\omega_n(z)} = \frac{1}{\left(1-\frac{z}{z_1}\right)\cdots\left(1-\frac{z}{z_n}\right)} =} \\ &\displaystyle{\left(1 + \frac{z}{z_1} + \left(\frac{z}{z_1}\right)^2 + \cdots \right)\cdots \left(1 + \frac{z}{z_n} + \left(\frac{z}{z_n}\right)^2 + \cdots \right) \ll} \\ & \quad \quad \quad \quad \displaystyle{(1+z+z^2+\cdots)^n = \frac{1}{(1-z)^n} = \sum_{k=0}^\infty \binom{n+k-1}{k} z^k} \end{array} $
ע"פ משפט מקדמי הבינום הכללי (General Binomial Theorem). זה
גורר בפרט ש
$latex \displaystyle |d_k|\leq\binom{n+k-1}{k},\quad |d_0|+\cdots+|d_m| \leq \sum_{k=0}^m \binom{n+k-1}{k}=\binom{n+m}{m} $
לסיכום, הוכחנו את אי השיוויון לסכומי חזקות הבא
$latex \displaystyle \max_{m+1 \leq \nu \leq m+n} |s_\nu| \geq \frac{|s_0|}{2^n \sum_{k=0}^m \binom{n+k-1}{k} - 1}=\frac{|s_0|}{2^n \binom{n+m}{m} - 1} $
עם מעט יותר דקדקנות בפרטים היינו יכולים להשיג את החסם האופטימלי
(שהוא מעט יותר טוב).
אני רוצה להציג לכם בעיה מחוץ לתחרות. אני חושש שאתם כבר שבעים
מבעיות מתמטיות, אך לזו אין זמן הגשה.
נתתי את הבעיה הזו בתחרות שוויצר (Schweitzer) ב - $latex {1976}$, השנה
שבה טוראן הלך לעולמו, והיא הוקדשה לזיכרו. טוראן היה אחד מהמארגנים
של התחרות ושוויצר היה סטודנט שלו, אשר נהרג על ידי הנאצים במלחמת
העולם השניה כאשר היה בתחילתה של קריירה מבטיחה. התחרות היא עבור
תלמידי אוניברסיטה בהונגריה, אך אני בטוח שתוכלו לפתור את הבעיה גם
כן; עקבו אחר דרך הפתרון של ההוכחה למעלה.
בעיה: הוכיחו את האי-שיוויון
$latex \displaystyle \max_{1 \leq |\nu| \leq n} |s_\nu| \geq \frac{|s_0|}{n} $
ללא שום תנאים על $latex {z_j}$ ו - $latex {b_j}$ מלבד הדרישה
$latex \displaystyle z_j \neq 0 \quad (j=1,\ldots,n) $
זה נידרש כי אנו מרשים גם חזקות שליליות.
נמשיך. תחום ההתעניינות העיקרי של טוראן היה תורת המספרים האנליטית.
לעיתים רבות במתמטיקה, במקום לתקוף את הבעיה שלך ישירות, ניתן להשיג
פתרון ע"י דרך עקיפה. (דוגמא לכך ראינו כאשר השתמשנו בדואליות בהוכחה
שנתנו קודם). דוגמה טובה לרעיון זה היא השיטה בה נחקרים המספרים
הראשוניים בתורת המספרים האנליטית ע"י שימוש בפונקציה יוצרת.
הפונקציה המתאימה היא פונקצית זטה של רימן (Riemann's zeta
function)
$latex \displaystyle \zeta(s) \overset{\text{def}}{=} \sum_{n=1}^\infty \frac{1}{n^s} $
היא מתקשרת למספרים ראשוניים ע"י הצגת אוילר כמכפלה אינסופית
(Euler's product representation)
$latex \displaystyle \zeta(s) = \frac{1}{1-\frac{1}{2^s}}\frac{1}{1-\frac{1}{3^s}} \cdots = \prod_{p} \frac{1}{1-\frac{1}{p^s}} $
כאשר במכפלה האינסופית המספרים במכנה רצים על כל המספרים הראשוניים.
קל לבדוק את הזהות הזו בצורה פורמלית: כל גורם הוא טור גיאומטרי
$latex \displaystyle \frac{1}{1-\frac{1}{p^s}} = 1 + \frac{1}{p^s} + \frac{1}{p^{2s}} + \cdots $
וכאשר פותחים סוגריים במכפלה האינסופית מתקבלים גורמים כגון
$latex \displaystyle \frac{1}{p_1^{k_1s} \cdots p_r^{k_rs}} = \frac{1}{n^s} $
כאשר
$latex \displaystyle n = p_1^{k_1} \cdots p_r^{k_r} $
כל מספר שלם מופיע בדיוק פעם אחת בצורה זו וכך אנו מקבלים את הצורה
המקורית של פונקצית זטה. הצגת אוילר היא על כן ניסוח אנליטי של המשפט
היסודי של תורת המספרים (Fundamental Theorem of Number Theory).
הרעיון הוא שניתן לחשב או לבחון את $latex {\zeta(s)}$ בהסתמך על הגדרתה ללא
איזכור של הראשוניים ואז להשתמש במידע שהתקבל עבור הראשוניים. למטרה
זו עלינו להיות מסוגלים לחשב גם במספרים מרוכבים: על פי תגליתו פורצת
הדרך של רימן באמצע המאה ה - $latex {19}$, מה שהוביל ללידתה של תורת המספרים
האנליטית, ההתנהגות של פונקצית זטה במישור המרוכב, במיוחד במקומות
שבהם היא מתאפסת, קשורה בקשר עמוק להתפלגותם של המספרים הראשוניים.
הוא שיער השערה לגבי המקומות שבהם פונקצית זטה מתאפסת, אשר נקראת
השערת רימן (Riemann's Hypothesis), ואשר שקולה לכך שהראשוניים
מתנהגים בצורה רגולארית. (זו היא רק אחת מהיוזמות של רימן; ניתן למצא
את שמו כמעט בכל תחום של המתמטיקה. לאור מה שאמרתי לגבי איך שטוראן
ראה את תפקידו הוא במתמטיקה, זה אינו פלא שהוא החשיב את רימן כגדול
המתמטיקאים בעת המודרנית.)
ההצלחה הראשונה של הגישה של רימן היתה ההוכחה של משפט המספרים
הראשוניים (Prime Number Theorem) ע"י הדמרד (Hadamard) ודה
לה וואלה-פוסן (de la Vallée-Poussin). אם נסמן, כפי שנהוג,
את מספר הראשוניים שהם קטנים או שווים ל - $latex {N}$ ע"י $latex {\pi(N)}$,
$latex \displaystyle \pi(N) \approx \frac{N}{\log N} \quad (N \rightarrow \infty) $
ישנם $latex {N}$ מספרים שלמים עד ל - $latex {N}$ ואנו רואים שהראשוניים הם פחות מכך
בגורם $latex {\log N}$; זהו הלוגריתם הטבעי של $latex {N}$ (natural
logarithm). השערת רימן מתקשרת לכמה טובה הערכה זו-או על מנת להיות
מדוייקים יותר, היא קשורה לקירוב טוב יותר ע"י פונקציה אחרת במקום
$latex {N/\log N}$-והיא עדיין פתוחה בימינו אנו. זו הבעיה הבולטת ביותר
בתורת המספרים, אם לא בכל המתמטיקה.
לא אוכל להסביר את הקשר בין $latex {\zeta(s)}$ והמספרים הראשוניים ביתר
פירוט. נסתפק בכך שנאמר כי לפונקציות מרוכבות יש גם נגזרות
ואינטגרלים, השונים בעיקרם מהמקרה הממשי, ותוכלו להבין את הקשר כאשר
תלמדו יותר על נושא זה.
כעת, טוראן רצה להוכיח לא פחות מאשר את השערת רימן. היה לו
רעיון מקורי על איך לתקוף אותה ורעיון זה הוביל אותו לעבר אי-
שיוויונות של סכומי חזקות. לכן, הם היו עבורו לא רק מטרה לשם עצמה.
הוא אף פעם לא התעניין בבעיות כבעיות. במתמטיקה שלו הוא תמיד דורבן
על ידי ישומים ועל ידי חשיבות הבעיה.
למרות שלא הצליח להשלים את מטרתו הסופית, על ידי אי-שיוויונות של
סכומי חזקות מורכבים יותר מזה שהוכחנו פה, הוא הצליח, למרות הכל, להשיג
תוצאות חדשות על ההתפלגות של מספרים ראשוניים והוא מצא מאוחר יותר
שאפילו אי שיוויונות פשוטים (כגון זה שראינו; מה שנקרא על ידו משפטו
הראשון) הם בעלי שימושים מעניינים בתחומים שונים של אנליזה ותורת
המספרים. זהו התוכן של חלקו השני של ספרו.
בהקשר זה אני נזכר במתמטקאי הונגרי בולט אחר בשם פול ארדש
(Paul Erdös). טוראן וארדש היו חברים טובים אך ארדש היה כמעט
ההפך מטוראן. הוא היה פותר בעיות ובאותה נשימה היה מתמטיקאי שהציג
בעיות מתמטיות חדשות והתעניין בבעיה המתמטית עצמה. טוראן פעמים רבות
הסתייג מכך שארדש נהג להתפזר על בעיות רבות כל כך ולא התמקד בבעיות
החשובות.
(טוראן לא לגמרי צדק, והוא ידע זאת. ארדש היה בעל יכולת יוצאת מן
הכלל לשים את האצבע, אולי באופן לא מודע, על הבעיה הנכונה ואכן בעיות
רבות הפכו להיות תחילתו של מחקר חדש וחשוב.)
לפעמים, טוראן גם עשה "שימושים" לא שיגרתיים במתמטיקה. במשך המלחמה
הוא היה עצור במחנה עבודה נאצי. בזמן שהוא תקע יתדות וסחב לבנים הוא
חשב על בעיות שיכול לפתור ללא ניר ועיפרון. זו היתה הדרך שבה הוא גילה
את משפטו המפורסם בתורת הגרפים. זו מתנה בעלת ערך רב להיות מסוגל
לעשות מתמטיקה כאשר חייך בסכנה ואינך יודע אם תחיה גם מחר. זה עזר לו
להחזיק מעמד במשך כמעט שלוש שנים של מאסר. הוא שמר על אהבתו לעשית
מתמטיקה עד ליום מותו והוא לא היה מסוגל להעביר יום מבלי לחשוב על
מתמטיקה, ללא קשר לכמה קשה היה היום ואפילו כשכבר היה מאוד חולה.
סיפור אמיתי נוסף הוא שמייד אחרי המלחמה הוא נעצר על ידי חיילים
רוסיים שביקשו את הניירות שלו. במקום זאת, הוא הראה להם מאמר שלו
שהתפרסם בירחון הרוסי איזבסטיה (Izvestiya) עם שמו שרשום שם
ברוסית. הם נתנו לו ללכת. הוא היה יכול באותה מידה לגמור בגולג אשר
בסיביר; אי אפשר היה לדעת בימים ההם.
לא היו לו חיים קלים גם אחרי המלחמה. הוא קיבל הרבה כבוד על עבודותיו
בצורת פרסים נחשבים, אך זה לא מנע מאנשים לצאת בביקורת פוליטית נגדו
במסווה של קידום מתמטיקה שימושית ודברים דומים וכך שהרבה מזמנו היקר
הוקדש להגנה על עצמו ועל המדע האמיתי שהוא ייצג.
הוא לא היה יכול לחזות זאת, אך לאמיתו של דבר זו היתה בחירתו האישית.
בשנת $latex {1948}$ הוא ביקר במכון ללימודים מתקדמים בפרינסטון ארה"ב
(Institute for Advanced Study at Princeton). זה המכון שבו
אינשטיין עבד לאחר שעזב את גרמניה ובו היו (ועדיין ישנם) רק הגדולים
ביותר בעלי משרה קבועה. לטוראן הוצעה משרה קבועה במכון. הוא היה יכול
לעבוד בתנאים הטובים ביותר שמתמטיקאי יכול לחלום עליהם. אבל, הוא
העדיף לקבל משרה באוניברסיטת בודפשט, שכן הוא ראה את עצמו כמתמטיקאי
הונגרי וחשב שזו היתה חובתו לחזור הביתה וליסד סביבו קבוצת תלמידים.
לסיכום, אני אומר שלא רק שהוא היה מתמטיקאי דגול, הוא גם היווה דוגמא
עבורנו למדען ובן אדם.
פונקציות הרמוניות
אורי בדר
דמייני דיסקת מתכת (נאמר מצילה של מערכת תופים) ששפתה מחוממת - בכל נקודה של השפה נשמרת טמפרטורה קבועה כלשהי (המשתנה מנקודה לנקודה). כיצד יתפשט החום מהשפה אל המרכז? ולאיזה טמפרטורה תגיע כל נקודה של הדיסקה?
פרשנות מתמטית לשאלה הראשונה ניתנה ע"י המתמטיקאי פורייה, אשר ניסח את משוואת החום בראשית המאה ה-$latex {19}$. המתמטיקאי פואסון הראה איך לפתור את השאלה השנייה. שניהם נסמכו על עבודות קודמות של לפלס$latex {^1}$ שחקר מחלקה של פונקציות הנקראות "הרמוניות" - פונקציות שערכן בכל נקודה ונקודה הנו ממוצע הערכים שמסביב. הטמפרטורה, כפונקציה על הדיסקה, לאחר שנסתיים תהליך התפשטות החום מהקצוות למרכז, מהווה פונקציה הרמונית.
על מנת לדון בפונקציות הרמוניות על דיסקה עלינו להשתמש בכלים של משוואות דיפרנציאליות. אנו נמנע מכך וננסה להבין פונקציות הרמוניות על מערכת סופית. בציור הבא $latex {140}$ ערוגות. עבור $latex {40}$ מתוכן - ערוגות השפה - נבחרו ערכים מספריים (הרשומים בתוכן).
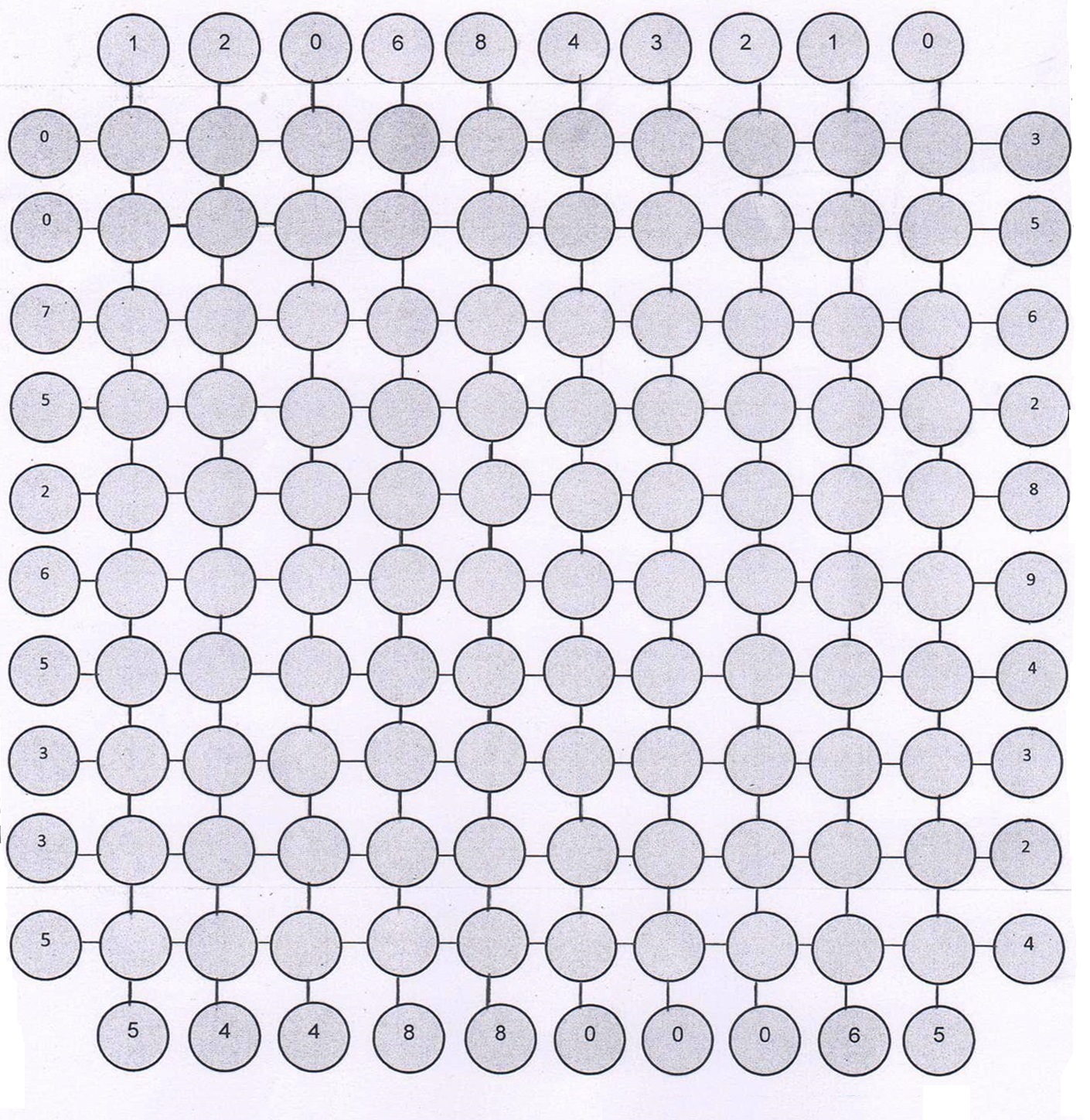
האם תוכלי לרשום מספרים בערוגות הפנימיות כך שהערך בכל ערוגה פנימית ישווה לממוצע הערכים בארבע שכנותיה? אם כן, בכמה דרכים שונות תוכלי לעשות זאת?
מערכת משוואות ליניאריות
אם נגדיר את ערכי הערוגות הריקות כמשתנים
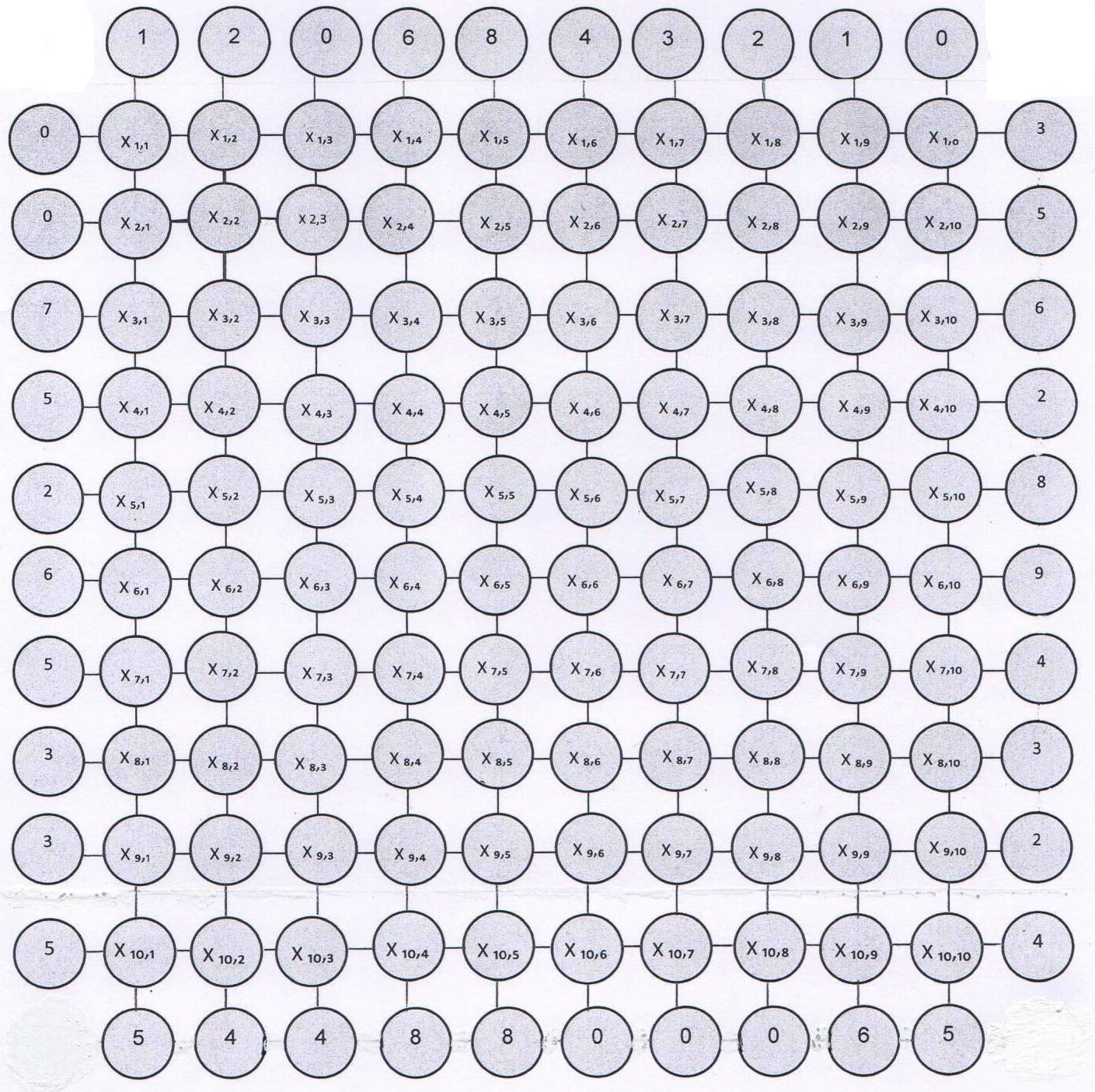
נוכל לרשום $latex {100}$ משוואות ב- $latex {100}$ נעלמים, לדוגמא:
$latex \displaystyle .X_{1,2}=\frac{1}{4}*2+\frac{1}{4}X_{2,2}+\frac{1}{4}X_{1,3}+\frac{1}{4}X_{1,1} \quad ,X_{5,5}=\frac{1}{4}X_{4,5}+\frac{1}{4}X_{5,6}+\frac{1}{4}X_{6,5}+\frac{1}{4}X_{5,4} $
תלמיד חטיבת ביניים חרוץ ובעל זמן פנוי יכול לרשום את כולן ולנסות לפתור אותן. האם יצליח?
מערכת המשוואות שירשום התלמיד נקראת "מערכת משוואות ליניאריות לא הומוגנית". "לא הומוגנית" מפני שישנם "איברים חופשיים" במערכת- ערכי השפה (בדוגמא לעיל, המספר $latex {\frac{1}{2}=\frac{1}{4}*2}$ המופיע במשוואה השנייה). אם נאפס אותם (נחליף את המשוואה השנייה שבדוגמא במשוואה $latex {X_{1,2}=\frac{1}{4}X_{2,2}+\frac{1}{4}X_{1,3}+\frac{1}{4}X_{1,1}}$ וכדומה), נקבל מערכת משוואות "הומוגנית".
המערכת ההומוגנית מתארת את הבעיה הבאה.

בעיה זו קלה לפתרון - אם נרשום $latex {0}$ בכל הערוגות נקבל פתרון כשר. פתרון זה נקרא "טריוויאלי"$latex {^2}$ . נותרה שאלת יחידות הפתרון: האם יתכן פתרון לא טריוויאלי?
טענה: למערכת המשוואות ההומוגנית הנ"ל אין פתרון לא טריוויאלי.
הוכחה: בהינתן פתרון כלשהו, נביט בערוגה המקבלת את הערך הגדול היותר. ערך זה הינו ממוצע הערכים השכנים. נובע שגם הערוגות השכנות מקבלות כולן ערך זה וגם שכנותיהן וגם שכנות שכנותיהן וכך הלאה. בקיצור, נובע שכל הערוגות שוות בערכן וערך זה, חייב להזדהות עם ערך השפה, $latex {0}$.
התחום המתמטי העוסק בפתרון מערכות של משוואות ליניאריות נקרא אלגברה ליניארית והוא נלמד בשנה הראשונה באוניברסיטה. אחד המשפטים הראשונים שנלמדים הוא המשפט הבא:
בהינתן מערכת משוואות לא הומוגנית, אם למערכת ההומוגניות המתאימה$latex {^3}$ אין פתרונות פרט לפתרון הטריוויאלי אז למערכת הלא הומוגנית קיים פתרון והוא יחידי.
קל להשתכנע שפתרון, אם קיים, הוא יחיד: אם קיימים שני פתרונות למערכת הלא-הומוגנית הרי שהפרשם הנו פתרון למערכת ההומוגנית ולפיכך $latex {0}$ בכל מקום.
מדוע אם כן קיים פתרון? לא נוכיח כאן את המשפט במקרה הכללי$latex {^4}$ אבל ננסה להסביר זאת במספר אפנים עבור הבעיה שלנו.
ערסל קפיצים
נדמיין לעצמנו כעת כי הציור מתאר רשת קפיצים - כל מקטע בין שתי ערוגות הנו קפיץ והקפיצים מחוברים לחישוקים - הערוגות. מתקבלת כך סבכה של קפיצים וחישוקים ולה $latex {40}$ חישוקים בקצותיה. זוהי רשת קפיצים אידיאלית: החישוקים חסרי גודל, לקפיצים מימד אורך בלבד והאנרגיה האצורה בכל קפיץ נתונה ע"י הנוסחא $latex {\frac{1}{2}kx^2}$, כאשר $latex {k}$ קבוע כלשהו ו-$latex {x}$ מציין את אורך הקפיץ (על פי חוק הוק (Hooke) הנלמד בשיעורי הפיזיקה). אם לא נתפוס את החישוקים שבקצוות, תתכווץ הרשת לנקודה… נתקע באדמה $latex {40}$ מוטות עץ במבנה רבוע המתאים לשפת סבכת הקפיצים. נשחיל את החישוקים שבקצוות על מוטות העץ ונקבע אותם, כל אחד בגובה המתאים לערך השפה הנתון בערוגה המתאימה. נקבל "ערסל קפיצים משופע" כבציור.
 איור: יואב מורג
איור: יואב מורג
הערסל בוודאי ירטוט קצת לאחר שנחבר אותו למוטות, אך לאחר זמן מה יתייצב. האמנם? למה? ובאיזה גובה יהיה כל חישוק?
"עקרון האנרגיה המינימלית" אומר שמערכת פיזיקלית תתאזן במצב בו האנרגיה הכוללת שבה תהיה מינימלית. עדות ויזואלית יפה לעקרון זה ניתן כאשר טובלים מסגרת מתכת באמבט מי סבון ומרימים אותה (בזהירות).
 צילום: ליהי דהן
צילום: ליהי דהן
תמונה זו מזכירה במעט את הציור לעיל, ולא במקרה. על פי עקרון האנרגיה המינימלית הערסל יתאזן במצב בו סכום האנרגיות האצורות בקפיצים יהיה מינימלי$latex {^5}$ .
כיצד תשתנה האנרגיה הפוטנציאלית הכוללת האצורה בסבכת הקפיצים אם נשנה את גובהו של חישוק פנימי בודד ונקבע את כל שאר החישוקים במקומם? אם נרשום את האנרגיה הכוללת כפונקציה של גובהו של אותו חישוק בודד, מתי היא תהיה מינימלית? (רמז: השתמש בחוק הוק ובמשפט פיתגורס. גזור את הביטוי שקבלת.)
לא קשה לוודא אם כן שקיים מצב יחיד בו האנרגיה הפוטנציאלית של ערסל הקפיצים שלנו תהיה מינימלית, ואם נרשום בכל ערוגה את גובהו של החישוק המתאים כאשר הערסל מאוזן במצב זה, יתקבל פתרון לבעייתנו.
הוכחנו אם כן שקיים פתרון לבעיה, אבל האם פתרנו אותה?
מקצה שיפורים
נחזור כעת בדמיוננו לערסל הרוטט, לפני שהתאזן. ניתן לחשוב על תנודותיו כעל תהליך המתכנס אל הפתרון המבוקש. בתחילת התהליך הערסל מונח ברובו על הארץ ורק קצותיו מחוברים למוטות בגבהים שונים - במצב זה אצורה אנרגיה רבה בקפיצים שבקצוות. אנרגיה זו מומרת לאנרגיה קינטית (הערסל מתרומם ונע למעלה) המומרת שוב לאנרגיה פוטנציאלית (הקפיצים הולכים ונמתחים) וחוזר חלילה. לאט-לאט מאבדת המערכת אנרגיה, עקב חיכוך הערסל עם האוויר, ומתקרבת למצבה המאוזן בו דנו בסעיף הקודם. זהו תהליך מסובך.
נשווה בדמיוננו תהליך פשוט יותר$latex {^6}$ . לשם כך נניח לערסל וננסה לתאר את פתרון הבעיה כגבולו של תהליך אינסופי הניתן ע"י סדרה של ניחושי פתרון ושיפורם ההדרגתי. ראשית נרשום 0 בכל הערוגות הפנימיות. אחרי שנייה נחליף את הרשום בכל ערוגה וערוגה (בו זמנית) בממוצע הערכים שהיו רשומים בשכנותיה. בשנייה הבאה נעשה זאת שוב. ושוב. ושוב…
באופן פורמלי נגדיר לכל $latex {i}$ ולכל $latex {j}$ בין $latex {1}$ ל-$latex {10}$, $latex {X^0_{i,j}=0}$ (האינדקס $latex {0}$ בראש המשתנה רומז שזהו הערך בזמן $latex {0}$), ונגדיר את $latex {X^n_{i,j}}$ כממוצע ערכי השכנים בזמן $latex {n-1}$:
$latex \displaystyle X^n_{1,2}=\frac{1}{4}*2+\frac{1}{4}X^{n-1}_{2,2}+\frac{1}{4}X^{n-1}_{1,3}+\frac{1}{4}X^{n-1}_{1,1} ,$
$latex \displaystyle X^n_{5,5}=\frac{1}{4}X^{n-1}_{4,5}+\frac{1}{4}X^{n-1}_{5,6}+\frac{1}{4}X^{n-1}_{6,5}+\frac{1}{4}X^{n-1}_{5,4} $
לדוגמא (בדוק): $latex {X^0_{5,5}=0}$, $latex {X^1_{5,5}=0}$ ו- $latex {X^2_{5,5}=0}$ בעוד ש- $latex {X^0_{1,2}=0}$, $latex {X^1_{1,2}=\frac{1}{2}}$ ו- $latex {X^2_{1,2}=\frac{9}{16}}$.
נשים לב שבכל רגע נתון ערך הערוגה קטן מממוצע ערכי שכנותיה (התוכל להוכיח זאת? זכור שערכי השפה שלנו אי שליליים). נובע שהערכים בכל ערוגה הולכים ועולים, ולפיכך הולכים ומתכנסים לערך גבולי. ערך גבולי זה חייב להוות פתרון לבעייתנו.
יופי, הבעיה פתורה. כן? לא! באמצעות התהליך שלנו נוכל למצוא קירוב לפתרון, אך לעולם לא נמצא את הפתרון עצמו… איך נוכל לדעת עד כמה אנחנו קרובים לפתרון?
צבא הנמלים
נבצע כעת ניסוי מחשבתי נוסף. נדמיין צבא של נמלים היושב בערוגה $latex {(2,3)}$. כל מהלך הניסוי מלכת הנמלים יושבת במקומה אך שאר הנמלים מטיילות על פני גן השבילים המתפצלים שלנו. בהתחלה יושבות כלן בערוגה $latex {(2,3)}$. בשנייה הראשונה $latex {\frac{1}{4}}$ מהנמלים צועדות למעלה, $latex {\frac{1}{4}}$ ימינה, $latex {\frac{1}{4}}$ למטה ו- $latex {\frac{1}{4}}$ שמאלה. בשנייה השנייה, מתוך הנמלים שפנו למעלה, $latex {\frac{1}{4}}$ שוב פונות למעלה, $latex {\frac{1}{4}}$ ימינה, $latex {\frac{1}{4}}$ למטה ו- $latex {\frac{1}{4}}$ שמאלה, וכך גם יתר הנמלים. וכך בכל שנייה ושנייה. נמלה עוצרת כאשר היא מגיעה לשפה, ומדווחת למלכה מהו ערך השפה אליו הגיעה. המלכה מחשבת בכל שניה ושניה מהו ממוצע ערכי השפה המדווחים. לאיזה ערך תגיע המלכה בסוף היום? נכון מאד, $latex {X^{86,400}_{2,3}}$.
הצבא צועד בסך בשיטה ובמשמעת. להבדיל, אם נבחר בנמלה אחת באקראי ונתמקד רק בה, יראה לנו מסלול צעידתה אקראי לחלוטין. אפשר לדמיין כאילו בכל שנייה היא מפילה גורל על מנת להחליט מה יהיה צעדה הבא$latex {^7}$ . אם נמלה ממשיכה לשוטט בין הערוגות הפנימיות לאחר $latex {86,400}$ שניות הרי שהיא חסרת מזל באופן קיצוני. לפיכך, בסוף היום תדווחנה כבר כמעט כל הנמלים על ערכים למלכה.
ואם תעצור המלכה את הניסוי אחרי יומיים, או אחרי שנה, האם תקבל ממוצעים שונים בהרבה מזה שתקבל בסופו של יום אחד? נקודת המבט ההסתברותית מאפשרת לנו לענות על שאלה זו: הפרש הממוצעים לא יעלה על התרומה המקסימלית לממוצע אשר עשויות להרים הנמלים שעדיין לא הגיעו לשפה בסוף היום, דהיינו ערך השפה המקסימלי ($latex {9}$) כפול ההסתברות לכך שנמלה תהיה חסרת מזל באופן קיצוני. זהו גודל קטן ביותר, כפי שהקורא יכול בקלות להעריך.
כעת בידינו גם דרך נוספת לראות שהגודל $latex {X^{86,400}_{2,3}}$ מקרב את פתרון הבעיה: אם תעצור המלכה את הניסוי אחרי יום ושנייה תקבל ערך ממוצע הקרוב מאד לערך שתקבל אם תעצרו אחרי יום בלבד; מצד שני, ערך זה ישווה לממוצע הערכים אותם תקבלנה בניסויים דומים מלכות השוכנות בערוגות השכנות - אפשר לחשוב על הניסוי הנערך ע"י מלכת $latex {(2,3)}$ כעל ארבעה ניסויים הנערכים שנייה מאוחר יותר ע"י מלכות $latex {(1,3)}$, $latex {(2,2)}$, $latex {(3,3)}$ ו- $latex {(2,4)}$.
אחרי ניסוי מוצלח שכזה אנחנו יכולים לנוח בסיפוק ולהיות מרוצים מעצמנו – מצאנו קירוב טוב מאד לפתרון הבעיה. למעשה עיון נוסף יאפשר לנו לראות שאם נעצור את הניסוי אחרי יומיים הקירוב שלנו יהיה טוב עד כדי כך שנוכל באמצעותו לדעת מהו פתרון הבעיה בודאות מלאה! איך? למה? זאת נשאיר לקורא. לפני שנפרד נסב רק את תשומת ליבו לכך שערכי השפה שבחרנו הנם מספרים שלמים - נובע שהערכים הפנימיים יהיו בהכרח מספרים רציונליים. מה אפשר לאמר על המכנה המשותף שלהם?
$latex {^1}$ מתמטיקאי ואסטרונום צרפתי. מסופר שלפלס נשאל ע"י נפוליאון הכיצד בעבודתו על יציבותה של מערכת השמש אין כל איזכור לאלוהים. "אין לי שום צורך בהנחה הזאת" ענה לפלס ביובש.
$latex {^2}$ בשפת המתמטיקאים "טריוויאלי" = "מובן מאליו".
$latex {^3}$ מערכת המשוואות המתקבלת כאשר מאפסים את האיברים החופשיים במערכת הנתונה.
$latex {^4}$ על מנת להוכיח את המשפט יש לחשוב על ה"איברים החופשיים" כפונקציה של הצבות ערכים במשתנים. לכל הצבה(של $latex {100}$ ערכים) תתאים רשימה(וקטור) של $latex {100}$ מספרים שאם הם יהיו האיברים החופשיים המשוואות תסופקנה. תמונתה של הפונקציה הנה תת מרחב $latex {100}$-מימדי של מרחב $latex {100}$ מימדי…
$latex {^5}$ בדיוננו אנו מתעלמים מהכבידה. למעשה, לערסל הקפיצים משקל, ומשקלו משפיע על שיווי המשקל אליו יגיע. על מנת לקבל מושג לגבי הבעיה אותה עלינו לפתור אם ניקח בחשבון את אפקט הכבידה, נסי למצוא מה הפונקציה שאת הגרף שלה מתאר חוט חשמל המתוח (לא מאוד) בין שני עמודי חשמל.
$latex {^6}$ בתהליך הפשוט המבוקש הערסל לא רוטט - הוא פשוט מתמתח ונפרש אט אט מגובה הקרקע ועד למצבו המאוזן. מבחינה פיזיקלית אפשר לקרב תהליך זה ע"י הגדלת החיכוך - אפשר להשקיע את הערסל בבריכת מים. או בבריכת דבש… ברשות הקורא אנו מעדיפים בשלב זה לזנוח את דימוי הערסל ולשוב לחיקה החמים של האלגברה.
$latex {^7}$ המתמטיקאים מכנים התנהגות שכזו "הילוך שיכור".
מציאות או דמיון - על ההתאזרחות של המספרים המרוכבים
ליאו קורי
אחד הרעיונות המתטיים שמעוררים באופן קבוע סקרנות והשתאות אצל כל מי שמתוודע אליו בפעם הראושנה הוא הרעיון של המספרים המרוכבים, ובפרט המספר ה"דמיוני" $latex i$, המסמל, כידוע, את הרעיון של $latex \sqrt{-1}$. לאחר שאנו לומדים שכל מספר המוכפל בעצמו הוא מספר חיובי, ולאחר שאנו מפנימים את הכלל הלא-טבעי כלל וכלל, "מינוס כפול מינוס שווה פלוס", אנו נדרשים להתמודד עם ייצור מזן חדש שעל ידי הכפלה בעצמו מניב מספר שלילי. כמו במקרים אחרים אפשר תמיד להתנחם במחשבה שגם לאורך ההיסטוריה מתמטיקאים מוכשרים ומתוחכמים ביותר התקשו להתמודד עם הרעיון הזה. דורות רבים של מתמטיקאים העדיפו להעמיד את השורשים של המספרים השליליים (ובעצם את המספרים השלילם בכלל) מחוץ לגבולות של הדיון המתמטי הלגיטימי. במחשבה ראשונית, התגובה הזאת טבעית ומתאימה. אם אנו מתבקשים לפתור את המשוואה $latex x^2 + 1 = 0$, נשמע הרבה יותר טבעי ושפוי לומר "זו משוואה שאין לה פתרון," מאשר לומר "התפרון למשוואה הוא $latex \pm\sqrt{-1}$". אבל עדיין במחשבה ראשונית, מה נומר ביחס למשוואה$latex x+3=0$? האם לגיטימי לקבוע שהפתרון למשוואה הוא $latex -3$? אולי עדיף להגיד גם כאן שאין פתרון? האם פתרון כמו $latex -3$ הוא יותר או פחות לגיטימי מאשר מ-$latex \pm\sqrt{-1}$ כפתרון למשוואה פשוטה למראה? או שאולי שניהם לא לגיטימיים?
דיונים מהסוג הזה התנהלו בין טובי המתמטיקאים לאורך ההיסטוריה ואפשר לומר שהם לא יושבו עד השליש האחרון של המאה ה-$latex 19$! אבל כאשר ניסו לסלק את $latex \sqrt{-1}$ מהדלת הראשית כייצור לא לגיטימי, הוא נכנס בחזרה ובכוח "דרך החלון", מה שלא הותיר ברירה למתמטיקאים אלא להמשיך לתהות ולדון במהותו ובמקומו הראוי במערכת. אחת הדוגמאות היפות לכך ניתן למצוא בעבודות של שני מתמטיקאים בני המאה ה-$latex 16$, ג'ירולמו קרדנו ($latex Girolamo~Cardano~1501-1576$) ורפאל בומבלי ($latex Rafael~Bombelli~1526-1572$) אשר עסקו, בין היתר, בפיתוח שיטות לפתרון משוואות בדרגה שלישית ורביעית. בספר של בומבלי, אשר בו הוא הציג את שיטותיו של קרדנו, אנו מוצאים את השאלה הבאה: "הקוביה שווה לחמישה עשר שורשים וארבעה מספרים." במונחים מודרניים מדובר בפתרון המשוואה $latex x^3=15x+4$. קל לראות שאחד הפתרונות למשוואה הוא $latex 4$ (ובדרך כלל הם התספקו במציאת פתרון אחד). אבל, כאשר פותרים על פי שיטתו של קרדנו מקבלים את התוצאה הבאה:
$latex x= \sqrt[3]{2+\sqrt{-121}} - \sqrt[3]{2-\sqrt{-121}}$
תוצאה מהסוג הזה (ואחרות שהופיעו בספרו של קרדנו) יצרו מצב מביך. קרדנו לא קיבל, באופן כללי, את מספרים שליליים (או שורשים שלהם) כמקדמים או כפתרונות לגיטימיים למשוואות שבהן עסק. אילו נשאל, הוא היה אומר שלמשוואה $latex x^2 + 1 = 0$ פשוט אין פתרון, וכך גם לגבי$latex x + 3 = 0$. אצלו לא הייתה משוואה מהסוג $latex x^2 - 4 = 0$, אלא רק $latex x^2 = 4$ (בעצם המשוואות שלו מנוסחות תמיד באופן מילולי בלבד, וללא סימנים אלגבריים). מצד שני, הוא בוודאי ראה את השיטות שלו לפתרון משוואות כלגיטימיות ונכונות. אז מה לעשות מול פתרון לגיטימי למשוואה (כלומר $latex 4$), אשר מתקבל תוך שימוש (בלתי נמנע) ביישות מתמטית לא לגיטימית (כלומר הבינום $latex 2+\sqrt{-21}$)? במקרים מהסוג הזה קרדנו הציע "שנעמיד בצד את העינויים השכליים הקשורים בכך", ופשוט נכפיל לפי הכללים לחישוב עם בינום שהיו ידועים בתקופה. קרדנו לא הסתיר את מבוכתו. הוא הצהיר שמדובר בפתרון "סופיסטי", שאותו כינה "חמקמק וגם חסר-תכלית". כלומר: קרדנו הסיק שאין לו ברירה אלא לקבל את השורשים של מספרים שליליים כלגיטימיים (ולו בהקשר מוגבל), על אף שהוא לא הבין כלל את "מהותם" של ייצורים מהסוג הזה.
לאחר תקופתם של קרדנו ובומבלי, שיטות החישוב עם שורשים של מספרים שליליים הלכו והשתכללו ללא הרף, אך בו בזמן גדלה המבוכה הכרוכה בנסיון להסביר את משמעותם המתמטית. שניוּת זו נמצאה לעיתים אצל אותו מתמטיקאי עצמו, והיא באה לידי ביטוי בולט במיוחד אצל הדמות המרכזית והמשפיעה ביותר של המתמטיקה והפיזיקה במאה ה-$latex 18$, הלוא הוא ליאונהרד אוילר ($latex Leonhard~Euler~1707-1783$). בין יתר הישגיו, אוילר הצליח להגדיר מחדש מושגים מרכזיים של החדו"א, בדרך שתתאים גם לשימוש מעשי ועקבי עם המספרים המרוכבים. כך היה, למשל, בנוגע להגדרת פונקציה מעריכית ולוגריתמית עבור מספרים שליליים או מרוכבים. הדוגמה הקלאסית שהדגימה את כוחם של רעיונותיו מופיעה במה שמכונה מאז "נוסחת אוילר":
$latex e^{i\pi}+1=0$
נוסחת אוילר מעוררת תמיד עניין רב ופליאה בגלל השילוב הנדיר בתוך תבנית אחת של חמישה מספרים "חשובים" $latex (e, i, \pi, 1, 0)$ ושני סימנים בסיסיים $latex (+,=) $. עצם הופעתו של אותו מספר "דמיוני", $latex \sqrt{-1}$, בכפיפה אחת עם כל האחרים, בשילוב כה יפה מבחינה מתמטית היה בו מעין מתן חותמת של לגיטימציה סופית ושל מעמד מתמטי זהה לזה של המספרים האחרים שבנוסחה. חותמת נוספת ניתנה בעבודותיו של אוילר בתחום אחר, תורת המספרים. גם כאן אוילר פתר מספר בעיות ע"י שימוש בטכניקה מפתיעה ומקורית שבה מספרים שלמים מפורקים לגורמים המכילים מספרים מרוכבים, כמו למשל במקרה
$latex 5=(1+2i)(1-2i)$
אבל אותו אוילר עצמו, האשף הגדול של השימוש במספרים המרוכבים בהקשרים חדשניים ובלתי צפויים, המשיך לנסח את ההגדרות הבסיסיות של מערכות המספרים בדרך לא מאוד שונה מזו של כל קודמיו, ולא בהצלחה רבה במיוחד. כך למשל באחד הספרים החשובים שלו מ-$latex 1770$ , $latex Vollst\ddot{a}dige~Anleitung~zur~Algebra$, שבו אנו קוראים את הדברים הבאים:
מכיוון שכל מספר שניתן להעלות בדעתנו הוא גדול מ$latex -0$ או קטן מ$latex -0$, או שהוא בעצמו $latex 0$, הרי שברור כי לא ניתן לדבר על שורשים של מספרים שליליים כעל מספרים אפשריים. עלינו לומר, על כן, שאלה מספרים בלתי-אפשריים. זה מוביל אותנו לרעיון של מספרים שמעצם טבעם הם בלתי-אפשריים. אלה מכונים בדרך כלל מספרים דמיוניים או מדומיינים מכיוון שהם קיימים אך ורק בדמיון . … אף על פי שהמספרים האלה, למשל $latex \sqrt{-4}$, הם מעצם טבעם לחלוטין בלתי אפשריים, יש לנו בכל זאת ידיעה מספקת אודותם, מכיוון שאנחנו יודעים שכאשר $latex \sqrt{-4}$ מוכפל בעצמו מקבלים את התוצאה $latex -4$. והידיעה הזו מספיקה כדי שנוכל לחשב בצורה נאותה עמם.
הניסוח של אוילר מעלה יותר שאלות משהוא משיב עליהן: למשל, אם המספרים האלה מתקיימים רק בדמיוננו, איפה בעצם מתקיימים כל יתר המספרים? בעולם האמפירי? בדמיון של אחרים? הציטוט הזה מפי אוילר מדגיש את הפער שנוצר בין היכולת המזהירה לטפל במרוכבים ולמצות את הפוטנציאל שלהם ככלי מחקרי מהמדרגה הראשונה, לבין ההתקדמות שהושגה בהבנת טבעם ובמתן הגדרה מספקת. הציטוט גם מדגיש שעבור אוילר הגדרה מדויקת בנוגע למהות מספרים מסוגים הייתה הרבה פחות חשובה מאשר הידיעה על חוקי הפעולה שלהם, והיכולת לעשות בהם שימוש פורה.
ואף על פי כן, מאמצים להבנה מעמיקה יותר של המספרים המרוכבים נמשכו כל העת. כיוון חשוב אחד התפתח בעקבות תובנה הנוגעת להבנת המספרים השליליים, שגם היא הושגה בקשיים מרובים ורק במאה ה-$latex 17$. לפי התובנה הזאת, הסימנים $latex +/-$ מסמנים לא יותר מאשר "כיוונים גיאומטריים" מנוגדים. המספרים הטבעיים, אם כן, אינם "טעביים" יותר מהשליליים. בתחילת המאה ה-$latex 19$ תובנה דומה פותחה עבור המספרים המרוכבים בעבודות נפרדות של מספר מתמטיקאים. ניסוח יפה אחד של הרעיון הבסיסי באינטרפרטציה הזו מופיע בטקסט מ-$latex 1806$ מאת הכומר אדריאן בוּאֶא ($latex Abbé~Adrien-Quentin~Buée~1748-1826$), אשר קשר ישירות את משמעות $latex \sqrt{-1}$ עם זו של הסימנים $latex +/-$, במילים הבאות:
אני מדבר על הסימן $latex \sqrt{-1}$ ולא על הכמות או על היחידה הדמיונית $latex \sqrt{-1}$. כי $latex \sqrt{-1}$ הוא סימן מסויים שאנו מצמידים ליחידה האמיתית 1, ולא כמות מסויימת בפני עצמה. מדובר בשם תואר חדש שמוצמד לשם עצם רגיל ומוכר, ולא בשם עצם חדש. הסימן הזה אינו מציין חיבור או חיסור. … כמות שמלוּוָה בסימן $latex \sqrt{r-1}$ איננה מתווספת, איננה נגרעת, ואינה שווה לאפס. התכונה המתוארת ע"י $latex \sqrt{-1}$ איננה מנוגדת לזו שמתוארת ע"י $latex +$ ואף לא לזו שמתוארת ע"י $latex -$. … $latex \sqrt{-1}$ פשוט מסמן כיוון ניצב [לכיוונים המסומנים ע"י $latex +$ וע"י $latex -$].
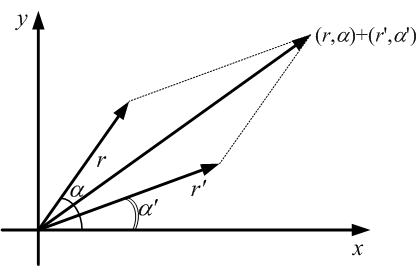
ז'אן ארגנד ($latex Jean-Robert~Argand~1768-1822$) הסביר ביתר פירוט איך לפרש את המספרים המרוכבים והפעולות בינהם בדרך גיאומטרית. מספר מרוכב $latex a+ib$ מתפרש כזוג $latex (r,\alpha)$, של קטע ישר בעל אורך $latex r $ וזווית $latex \alpha $ המייצגת כיוון על פני המישור. קל לראות בתרשים הבא, את הקשר בין שתי הדרכים לכתוב את המספר המרוכב: $latex r(\cos\alpha + i\sin\alpha) = a+ib$, כאשר $latex r^2=a^2+b^2$.
(תרשים 1):
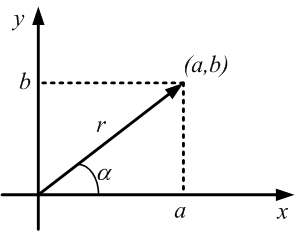
תרשים 1: ייצוג גיאומטרי של מספר מרוכב, על פי ארגנד: $latex a + ib = r(\cos \alpha + i\sin \alpha)$
ארגנד הגדיר גם את הפעולות הבסיסיות שניתן לבצע על המספרים המרוכבים: סכום של מרוכבים מתבצע דרך "חוק המקבילית", מכפלה דרך המשך הסיבוב והארכת האורך $latex r$
(תרשים 2):
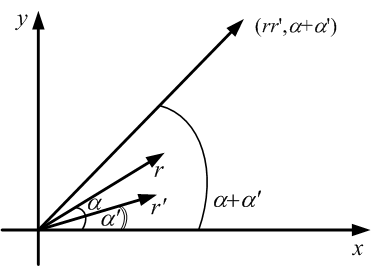
תרשים 2: סכום ומכפלה שלמספרים מרוכבים
חילוק והוצאת שורש מוגדרים באופנים דומים לאלה. במונחים אלה, המספר $latex \alpha \sqrt{-1}$ מתפרש, אם כן, כקטע ישר באורך $latex \alpha$ שמסובב $latex 90^\circ$ נגד כיוון השעון, בדיוק כפי ש בוּאֶא הגדיר בעבודתו.
מתן פירוש גיאומטרי למספרים המרוכבים היה דבר חשוב מכיוון שמאז תקופת יוון העתיקה הגיאומטריה נחשבה לענף המתמטי שהוודאות שלו לא הייתה מוטלת בספק. האירתמקטיה על ענפיה השונים, ומאוחר יותר גם האלגברה, נחשבו מאז תקופת אאוקליד לענפי ידע הנזקקים לתמיכה מן הגיאומטריה כדי לבסס את הלגיטימיות שלהם. דווקא בתחילת המאה ה- $latex 19$ המצב הזה התחיל להתהפך. תהליכים חשובים שהתרחשו בענפים מרכזיים של המתמטיקה (במיוחד עלייתן של הגיאומטריות הלא-אאוקלדיות, והעיסוק בשאלות הנוגעות למושגי היסוד של החדו"א) המשיכו לערער בהדרגה את מעמד הבכורה של הגיאומטריה כמקור עליון לוודאות המתמטית. באופן אירוני, אם כן, האינטרפרטציה הגיאומטרית של המרוכבים התגבשה בתקופה שבה היא יכלה להיתפש יותר כאילוסטרציה טובה לאופן התנהגותם המתמטית של המרוכבים, ופחות כביסוס איתן המסיר ספקות באשר ללגיטימיות שלהם. באותה תקופה התפתחה באיים הבריטיים מסורת מתמטית חדשה, מסורת "האלגברה הסימבולית", אשר חיפשה את יסודות האלגברה בניסוח חוקי פעולה מופשטים, בלא תלות במגבלות הנובעות מטבעם של הגדלים המעורבים בפעולות הללו. על פי היגשה הזו, לא נחוצים הסברים אודות מהותם של המספרים כדי להבין את תכונותיהם ואת חוקי הפעולה בהם, אלא ההיפך המוחלט: היא מכתיבה מראש את כללי ההתנהגות הרצויים של המערכות בהן היא דנה ובונה אותן בהתאם. על רקע הגישה הזו צמחה הגדרה חדשה ופורצת דרך להבנת המספרים המרוכבים והיא הופיעה ב- $latex 1837$ בעבודתו של המתמטיקאי האירי המפורסם סר וויליאם רוואן המילטון ($latex William~Rowan~Hamilton~1805-1865$).
נקודת המוצא של המילטון לתהליך בניית המרוכבים הייתה במערכת המספרים הממשיים וכללי האריתמטיקה שלהם. המילטון הניח את אלה כידועים וכלא טעונים שום הסבר או צידוק נוספים. על בסיס האריתמטיקה הידועה של הממשיים, אפשר להתקדם ולהגדיר מערכת של זוגות סדורים של מספרים מששיים$latex (a,b)$. בהגדרה כזו אין נסיון להסביר או להנהיר מערכת פחות או יותר מוכרת, אלא לבנות אותה מן היסוד, באופן פורמלי ולפי כללים מוכתבים, ללא שום הסבר נוסף. כך, על הזוגות הללו ניתן להגדיר פעולות אריתמטיות שמקיימות תכונות דומות לאלה של הממשיים, אבל שמחקים גם את התכונות הרצויות למרוכבים. פעולות אלה, כזכור, נגזרות מהפעלת כללי פעולה אלגבריים פשוטים על ביטויים מהסוג $latex a+ib$, עם תוספת אחד חשובה, דהיינו, התכונה הבסיסית של מה שמסומן באות $latex i$, דהיינו: $latex i^2 =-1$.
הסכום והמכפלה של מרוכבים, אם כן, מוגדרים כך:
(*) $latex (a_1+ib_1)+(a_2+ib_2)=(a_1+a_2)+i(b_1+b_2)$
(**) $latex (a_1+ib_1)(a_2+ib_2)=(a_1+a_2-a_2+ib_2)+ia_1(b_2+a_2b_1)$
פעולת החילוק מתבצעת מתוך עקרון דומה לזה הנהוג בחילוק של מספרים שלמים. כך, כדי לחלק מספר שלם $latex p$ במספר שלם אחר,$latex q$, מה שנדרש הוא להכפיל את $latex p$ ב"הופכי" של $latex q$. וההופכי של $latex q$ (ביחס למכפלה של שלמים) הוא, כמובן$latex \frac{1}{q}$ , כי $latex p*\frac{1}{q}=1$. ולכן, אם מחלקים את $latex p$ ב- $latex q$מקבלים $latex \frac{p}{q}$. כך גם במקרה של המרוכבים: חילוק במספר $latex a+ib$ שקול להכפלה במספר "ההופכי" שלו (ביחס למכפלת מרוכבים). אנחנו נדרשים למצוא מספר מרוכב אחר, $latex a'+ib'$, המקיים את התנאי הבא: $latex (a' +ib')*(a+ib)=1$. עם מעט עבודה אלגברית קל לראות שהערך של $latex a'+ib'$ חייב להיות
(***) $latex \left(\frac{-b}{a^2+b^2}\right)+\left(\frac{a}{a^2+b^2}\right)=a'+ib'$
כל זה היה ידוע היטב בעת שהמליטון ניגש להציע את גישתו החדשה להגדרת המרוכבים, אבל דיונים רבים התקיימו בשאלת "מהותו" של המספר $latex i$, ושל כל המרוכבים בכלל, ומה הצידוק לשימוש בפעולות הללו. המילטון ביקש בכלל לעקוף את כל הדיון הזה ולא לשאול על ציקוד, אלא לקבוע ע"י הגדרה של פעולות על זוגות סדורים של ממשיים $latex (a,b)$, באופן פורמלי לחלוטין. וכך הוא הגדיר את הפעולות:
(§) $latex (a_1,b_1)+(a_2,b_2)=(a_1+a_2,b_1+b_2)$
(§§) $latex (a_1,b_1)*(a_2,b_2)=(a_1b_2-a_2b_2,a_1b_2+a_2b_1)$
(§§§) $latex (a_1,b_1):(a_2,b_2)=(a_1,b_1)\left(\frac{-a_2}{a_2^2+b_2^2},\frac{-b_2}{a_2^2+b_2^2}\right)$
ברור מראש ששלוש הפעולות (§)-(§§§), מניבות תוצאות זהות לאלה של (*)-(***). אלא שכאן הייצור המסתורי $latex i$ פשוט נעלם כלא היה. במערכת הזוגות הסדורים של המילטון, המספרים הממשיים מיוצגים ע"י זוגות מהסוג $latex (a,0)$, בעוד שהמספרים ה"דימיוניים" מיוצגים ע"י זוגות $latex (0,b)$. אפשר בכלל להשתמש בשמות אחרים, פחות טעונים מאלה כדגון "שליליים, דימיוניים" וכו', אבל אלה נאשרו בשימוש רק מכח ההרגל. בפרט, אם מבצעים לפי הכללים של המילטון את המכפלה $latex (0,1)*(0,1)$ הרי שמקבלים את התוצאה $latex (-1,0)$. במילים אחרות, הזוג $latex (0,1)$ מייצג בפועל את $latex \sqrt{-1}$ (או את i), כי אם מכפילים $latex (0,1)$ בעצמו מקבלים $latex -1$ , כפי שכל קורא יכול לבדוק בעצמו, דרך הכללים (§)-(§§§). קיומו של $latex i$ מתגלה בשיטה של המילטון מתוקף הפעלה פורמלית של פעולות, והבנת "תכונותיו", כביכול, לא נדרשת כתנאי לבניית המערכת כולה. "תכונותיו" הן, בעצם, מה שמערכת הפעולות המוגדרות באופן פורמלי מגות לנו.
אבל למרות הדגש הפורמלי שמאחורי התיאור הזה, אחד ההיבטים מעניינים ביותר בהגדרה של המילטון הוא שהיא השתלבה בצורה טבעית במיוחד עם עיסוקיו העיקריים האחרים בתחום האסטרונומיה והפיזיקה המתמטית (בעיקר אופטיקה ומכניקה)! המילטון היה כמובן בקיא בשימוש הפורה של אוליר במרוכבים במסגרת בחדו"א, אבל ההגדרות שהוא הכיר בתחילת דרכו המדעית למערכות המספרים השונות לגמרי לא הניחו את דעתו. סביב $latex 1828$ הוא התוודע לאינטרפרטציה הגיאומטרית של ארגנד. מיד עלה בדעתו הרעיון, כמה מועיל לצרכי מחקריו בפיזיקה מתמטית יכול היה להיות, אילו הצליח להרחיב את השיטה של ארגנד למצב של שלושה מימדים, כך שיתאפשר להגדיר את כל הפעולות האלגבריות על קטעי ישר בעלי אורך וכיוון במרחב (לעומת המישור, כמו במקרה של ארגנד). מתוך מוטיבציה זו, לניסוח משוכלל של חוקי יסוד בפיזיקה ותיאור תנועות של גופים צפידים במרחב, המילטון חיפש לפתח מקבילה לרעיון המרוכבים, אבל בשלושה מימדים. כלומר, כשם שבמסגרת המרוכבים הוגדרו פעולות של סכום, כפל, וחילוק, על מספרים $latex (a,b)=a+ib$, כך חיפש המילטון את הגדרתן עבור השלשות $latex (a,b,c)$. דרך אחת לעשות זאת, שעולה מיד על הדעת, היא להוסיף אלמנט דמיוני חדש, $latex j$, המשחק תפקיד דומה לזה של $latex i$, והמאפשר לסמן את המקום השלישי בשלשה באופן הבא: $latex a+ib+jc$. קל להגדיר את סכום של שתי שלשות כאלה, בדומה להגדרה שנהוגה במרוכבים לצורך זה:
$latex (a_1+ib_1+ic_1)+(a_2+ib_2+ic_2)=(a_1+a_2)+i(b_1+b_2)+j(c_1+c_2)$
אבל הבעיה עליה שקד המילטון לאורך זמן רב הייתה איך ניתן להגדיר מכפלה וחילוק באופן מלא עבור השלשות הללו. נדרשת כאן פעולת כפל שבה לכל שלשה $latex a+ib+jc$ קיימת שלשה אחרת, $latex a'+ib'+jc'$, וכך שאם מכפילים את השתיים מקבלים את התוצאה, $latex 1+i0+j0$ , כלומר$latex 1$ . (בדיוק כפי שתוצאת המכפלה של מספר ממשי $latex a$ במספר $latex a/1$ היא $latex 1$, ותוצאת המכפלה של המספר המרוכב $latex a+ib$ במספר $latex \left(\frac{-b}{a^2+b^2}\right)+i\left(\frac{a}{a^2+b^2}\right)$ היא $latex 1+i0$). לאחר ההצלחה בהגדרת הפעולות עם המרוכבים, לא נראה על פניו שצריכה הייתה להיות בעיה מהותית במציאת ההגדרה הנכונה לפעולות אם השלשות, אך על אף מאמציו הרבים, המילטון לא הצליח במשימה, ובדיעבד התברר שלא בכדי, כפי שאסביר בהמשך. אולם, חיפושיו של המילטון הובילו אותו לפריצת דרך מפתיע נוספת, הלוא היא מערכת הקווטרניונים (Quaternions). זו מערכת מהסוג שאותו חיפש המילטון, ובה הרחבה של רעיון המרוכבים, אלא שהיא לא הרחבה לשלשות, כי אם לרביעיות של מספרים ממשיים. גם המחיר שנאלץ לשלם לצורך בניית המערכת הזו היה מפתיע וחדשני.
המילטון כתב רביעייות של מספרים ממשיים, $latex (a,b,c,d) $ , בעזרת שלושה סימנים מיוחדים, $latex i,j,k$, כהרחבה לרעיון של$latex i$ המוכר מן המרוכבים. הרביעייה נכתבת באופן הבא: $latex a+ib+jc+kd $. הוא הגדיר באופן פורמלי פעולה בין הסימנים, על פי הכלל היחיד הבא: $latex i^2=j^2=k^2=ijk=-1 $. על בסיס הכלל הזה ניתן להכפיל שתי רביעיות באופן הבא:
$latex (a_1+ib_1+jc_1+kd_1)(a_2+ib_2+jc_2+kd_2) = A+iB+jC+kD $
כאשר:
$latex A=a_1a_2 - b_1b_2 - c_1c_2 - d_1d_2; B= a_1b_2 + b_1a_2 + c_1d_2 - c_2d_1; $
$latex C=a_1c_2 + c_1a_2 + d_1b_2 - d_2b_1; D= a_1d_2 + d_1a_2 + b_1c_2 - b_2c_1; $
ההגדרה נראית אולי מסורבלת במבט ראשון, אבל יש במבנה ארבעת הביטויים $latex A,B,C,D $ , סימטריה די ברורה ואפילו פשוטה. מה שחשוב באמת הוא שתחת ההגדרה הזו של מכפלה ניתן בהחלט למצוא פעולה הפוכה של חילוק, כפי שהמילטון חיפש. אבל מה שהתברר מיד להמילטון, וזה דבר מאוד מפתיע, הוא שהמכפלה הזו איננה קומוטטיבית! את זאת ניתן לראות בדוגמה פשוטה הבא:
$latex (1-i+j+k)(1+i+j+k) = 4j$ ואילו $latex (1+i+j+k)(1-i+j+k) = 4k$
ובמבט בסיסי עוד יותר, בהכפלת זוגות מתוך $latex i,j,k$, שינוי הסדר מניב שינוי בסימן התוצאה:
$latex ij=k=-ji~~~~~ jk=i=-kj~~~~~ ki=j=-ik $
מכפלת הקווטרניונים, אם כן, מספקת הפתעה מרעננת וחשובה: על אף שהיא מוגדרת היטב, על אף שהיא מקיימת תכונות אלגבריות בסיסיות, כמו הכלל האסוציאטיבי $latex [X*(Y*Z)=(X*Y)*Z] $; ועל אף שניתן להגדיר עליה פעולה הפוכה (כלומר חילוק), היא איננה מקיימת את כלל הקומוטטיביוּת $latex [X*Y=X*Y]$. וזה חידוש מרחיק לכת בהחלט! כלומר, המילטון הבין שניתן אמנם לבנות את המערכת המבוקשת של רביעיות עם פעולות של סכום, כפל וחילוק, אבל בתנאי שמוותרים על דרישת החילופיות, דרישה שהייתה מובנת מאליה כחלק מכל מערכת מספרית שניתן להעלות על הדעת. האלגברה החדשה שבנה המילטון, אלגברת הקווטרניונים, הייתה יצירה מהפכנית שהרחיבה את מושג המספר בכיוון בלתי צפוי, ובעצם פתחה את הדלת לחשיבה הרבה יותר רחבה על מערכות מופשטות, מוכללות והולכות. אי-אפשר, אגב, שלא להזכיר כאן את אחד הסיפורים הידועים בתולדות המתמטיקה, שהובא מפי המילטון עצמו, על רגע הגילוי של הקווטרניונים, שפרץ בתודעתו "כרעם ביום בהיר", כאשר צעד עם ליידי המילטון לאורך התעלה המלכותית בדבלין. מרוב התלהבות על סגירת מעגל של חמש-עשרה שנות מאמץ, לא התאפק המילטון, ובמעשה "מאוד לא פילוסופי" חרט את הנוסחה היסודית על אחת מאבני הגשר: $latex i^2 = j^2 = k^2 = ijk = -1 $.
המצאת הקווטרניונים כמושג מורחב ומוכלל של מערכת מספרים לא היה אירוע בודד בתקופתו. המתמטיקאי הגרמני הרמן גינטר גראסמן $latex (Hermann~G\ddot{u}nther~Grassmann~1809-1877)$, למשל, עסק במערכות מספרים מורחבות ומופשטות תוך פיתוח רעיונות מתמטיים מקוריים למדי. אולם, בשל כתיבתו המסורבלת הם לא זכו להתעניינות כלל בתקופתו, ורק מאוחר יותר הם שימשו להשראה ולנקודת מוצא לעבודות רבות וחשובות בתחום האלגברה. גם מספר מתמטיקאים בריטים מובילים פיתחו וחקרו באותה תקופה סוגים אחרים של מערכות מספרים מוכללים בעלי תכונות מסוגים ושמות שונים ומשונים, שבראייה לאחור ניתן לזהות את כולם תחת השם הכוללני-משהו, המקובל גם היום, "מספרים היפר-מרוכבים" $latex (Hypercomplex) $. אלה הופיעו בעבודות של ארתור קיילי $latex (Arthur~Cayley~1821-1895) $, ג'יימס ג'וזף סילבסטר $latex (James~Joseph~Sylvester~1814-1897)$, וויליאם קליפורד $latex (William~Kingdon~Clifford~1845-1879)$, ורבים אחרים. אבל, בטווח הקצר, היו אלה הקווטרניונים של המילטון שזכו להתעניינות הרבה ביותר וזאת מסיבה לגמרי בלתי צפויה, אם כי מבורכת מאוד מבחינת המילטון: הקווטרניונים התבררו ככלי יעיל במיוחד לניסוח חסכוני ומדוייק של תורות פיזיקליות רבות שהתפתחו בעת ההיא. המילטון פרסם ב-$latex 1853$ ספר מקיף, $latex Lecture on Quaternions$, שבו הציג בפירוט את הגדרת המרוכבים כזוגות של ממשיים, יחד עם תורתו החדשה. אולם, היה זה דווקא דרך ספריו של ידידו הסקוטי, פטר גותרי טייט$latex (Peter~Gurthrie~Tait~1831-1901) $, שהקוורטניונים זכו לתפוצתם הרבה ולהכרה ככלי יסוד לפיזיקה המתמטית המשגשגת של התקופה. זמן לא רב לאחר מכן, הקוורטניונים אבדו מחשיבותם ככלי לניסוח תורות פיזקליות כאשר, בתחילת המאה העשרים, שיטות אחרות, ובראשם החשבון הווקטוֹרים (vectors) החדש, הוכיחו את עצמם כיעילים וכעדיפים לאותם משימות שהקווטרניונים שימשו נאמנה בתקופה שמעל לשלושה עשורים.
השערת להמר
יוסי כהן
חרגול עומד על שעון בשעה $latex {12}$, ומתחיל לקפוץ, בדילוגים של מספרים שלמים. אם יקפוץ כל פעם שעה אחת, הוא יגיע כמובן לכל השעות השלמות. אם יקפוץ בדילוגים של $latex {2}$, הוא יגיע רק לשעות הזוגיות. שאלה: אילו דילוגים יבטיחו שיגיע לכל סימוני השעות השלמות?
ניקח לדוגמה דילוג של 5. עקבו ובדקו אם אני צודק: הוא יגיע על פי סדר לשעות $latex {5, 10, 3, 8, 1, 6, 11, 4, 9, 2, 7}$ ואז יחזור לשעה $latex {12}$ (שהיא בעצם $latex {0}$). כלומר - בדילוגים של 5 אכן יעבור על פני כל השעות השלמות.
גם דילוגים של 7 טובים (זה בעצם לדלג 5, רק בכיוון ההפוך), וגם $latex {11}$ (שזה לדלג 1, נגד כיוון השעון). אלו המספרים היחידים - $latex {1, 5, 7, 11}$. מה משותף להם? אלה הם המספרים הקטנים מ-$latex {12}$ וזרים ל-$latex {12}$, שפירושו שאין להם ול-$latex {12}$ מחלק משותף גדול מ-$latex {1}$. מתברר שלמספרים הקטנים ממספר נתון וזרים לו יש תפקיד מיוחד. הם מעניינים. כדי לדבר עליהם, נצטרך כמה הגדרות.
הגדרה. נאמר שמספר טבעי (כלומר מספר שלם לא שלילי) $latex {d}$ מחלק את המספר הטבעי $latex {n}$ אם קיים מספר $latex {m}$ כך ש-$latex {n=md}$. אם $latex {d}$ מחלק את $latex {n}$ נרשום $latex {d|n}$. אם לא, נסמן $latex {d\not | \ n}$.
למשל, $latex {5|15}$ אבל $latex {5\not | \ 13}$ . נזכיר שמספר ראשוני הוא מספר טבעי הגדול מ-$latex {1}$ שמחלקיו היחידים הם $latex {1}$ והוא עצמו. שישה המספרים הראשוניים הראשונים הם $latex {2, 3, 5, 7, 11, 13}$. מספר שאיננו ראשוני נקרא פריק.
הגדרה. נאמר כי לשני מספרים טבעיים $latex {m}$ ו- $latex {n}$ יש מחלק משותף גדול מ-$latex {1}$ אם קיים $latex {d\neq1}$ כך ש-$latex {d|n}$ ו-$latex {d|m}$ . אם אין $latex {d}$ כזה אומרים ש-$latex {m}$ ו-$latex {n}$ זרים.
המתמטיקאי הגדול של המאה ה-$latex {18}$, לאונרד אוילר $latex {(1707 - 1783)}$ גילה שיש משמעות מיוחדת למספר המספרים הטבעיים הזרים ל-$latex {n}$ וקטנים ממנו. הוא סימן את המספר הזה ב-$latex {\varphi(n)}$. כיום קוראים למספר הזה "פונקציית אוילר", למשל, ראינו ש-$latex {\varphi(12)=4}$ , משום שהמספרים הקטנים מ-$latex {12}$ וזרים לו הם $latex {1, 5, 7}$ ו-$latex {11}$. הנה כמה ערכים נוספים: $latex {\varphi(2)=1}$, $latex {\varphi(3)=2}$, $latex {\varphi(4)=2}$ (כי המספרים הקטנים מ-4 וזרים לו הם 1 ו-3) $latex {\varphi(5)=4}$ , $latex {\varphi(6)=2}$, $latex {\varphi(7)=6}$. (שימו לב כי $latex {\varphi(5)=\varphi(12)=4}$ האם יש לכם עוד דוגמאות כאלה?)
עובדה פשוטה אם $latex {p}$ הוא מספר ראשוני, אז כל המספרים הקטנים ממנו זרים לו, ולכן $latex {\varphi(p)=p-1}$ . ומה בדבר פונקציית אוילר של מכפלת שני ראשוניים? נסו דוגמאות והיווכחו: לכל שני מספרים ראשוניים $latex {p}$ ו - $latex {q}$ מתקיים $latex {\varphi(pq)=(p-1)(q-1)}$ (האם תוכלו למצוא את $latex {\varphi(33)}$? $latex {\varphi(35)}$?) האם תוכלו למצוא שני מספרים $latex {m}$ ו-$latex {n}$ שעבורם $latex {\varphi(mn)\neq \varphi(m)\varphi(n)}$ האם תוכלו לנחש לאילו מספרים $latex {m}$ ו-$latex {n}$ כן מתקיים שוויון?
קל לראות שאם $latex {n}$ איננו מספר שאיננו ראשוני אז $latex {\varphi(n)\neq n-1}$. המתמטיקאי האמריקני דיק להמר ($latex {1905 - 1991}$ - להמר היה גם מחלוצי מדעי המחשב) שיער משהו חזק יותר.
השערת להמר $latex {(1932)}$ אם $latex {n}$ אינו ראשוני אז $latex {\varphi(n) \not | \ n-1}$.
שמונים שנים עברו מאז פרסם להמר את השערתו, וההתקדמות בהשערה מעטה. במאמר שבו הציג להמר את השערתו הוא ציין גם שקיימים שמונה מספרים טבעיים פריקים $latex {n}$ כך ש- $latex {\varphi(n)| n+1}$ .(האם תוכלו למצוא כמה כאלה? שימו לב למשל ש-$latex {15}$ הוא כזה). ההשערה כיום גורסת שאין יותר כאלה.
להוכחת השערת למר נוקטים כיום בשני כיוונים עיקריים:
1. רעיון שהתחיל איתו כבר להמר(באותו מאמר ששיער את ההשערה, ראה[1]): ניסיון להראות שאם קיימים $latex {n}$-ים כאלה אזי מספר הגורמים הראשוניים שלהם הוא גדול יחסית (התוצאה האחרונה מדברת על $latex {14}$ גורמים ראשוניים לפחות) .
2. רעיון של קרל פומרנץ([2]) מעין הכללה: מציאת חסם עליון למספר ה- $latex {n}$ ים הקטנים מ-$latex {x}$ כך ש-$latex {\varphi(n)|n-a}$ ל- $latex {a}$ כלשהו (בהשערה המקורית $latex {a=1}$) התוצאה העדכנית מדברת על כך שיש לכל היותר $latex {\sqrt(x)}$ (בערך) כאלה.
1. D. H. Lehmer, On Euler's totient function, Bull. Amer. Math. Soc., 38 (1932), 745-751.
2. C. Pomerance, On the congruences $latex {\sigma(n)\equiv a (mod n)}$ and $latex {n\equiv a (mod \varphi(n))}$, Acta Arith. 26 (1975), 265–272.
3. Richard K. Guy, Unsolved Problems in Number Theory, 3rd ed. springer, New York 2004.
אדמונד לנדאו: סיפור עם הוכחה
אליהו לוי
לנדאו וביברבך - הוכחה שאי אפשר לחלק זוית כללית לשלושה ע"י סרגל ומחוגה, ופרשה עצובה בצידה
אליהו לוי (לפי הצעת פרופ' בנימין וייס מהאוניברסיטה העברית)
תקופת הנאצים הביאה סבל רב למתמטיקאים יהודים, גם כאשר לא הגיע הדבר לרצח ממש.
בין המתמטיקאים הגרמנים שלא סומנו ע"י המשטר הנאצי כיהודים או יהודים למחצה או לרבע או כבעלי פוליטיקה לא רצויה, היו כאלה ששיתפו פעולה עם המשטר ואף תמכו במשטר הנאצי בהתלהבות. אחד המתמטיקאים הגרמנים הגדולים שהביע תמיכה במשטר הנאצי ובעמדותיו היה לודביג ביברבך ($latex Ludwig~Bieberbach~1886-1982$) שכתב מאמרים המקשרים גזע ומתמטיקה ברוח המשטר.
ידועה פרשת הצקותיהם של פעילים נאצים מבין הסטודנטים בגטינגן (שהיתה המרכז המתמטי העולמי עד שעליית הנאצים מחקה אותו) בתחילת שנות ה-1930 למתמטיקאי היהודי-גרמני הגדול אדמונד לנדאו ($latex Edmund~Landau~1877-1938$), מכוכבי המכון בגטינגן, עד שהטרדות אלה אילצו אותו לפרוש ב-1933, דבר שכאב לו מאוד.
כדאי להתעכב קצת על אדמונד לנדאו, מגדולי תורת המספרים האנליטית ותורת הפונקציות המרוכבות בדורו, שבהן היו לו תוצאות רבות והספרים שכתב נחשבו למופת, ומאידך בעל תפקיד מיוחד בהיסטוריה של המתמטיקה הישראלית. הוא פתח את מכון איינשטיין למתמטיקה באוניברסיטה העברית בכך ששימש שם פרופסור בסמסטר חורף 1927-28. העובדה שמתמטיקאי "טהור" כה גדול היה מעורב בכך, היתה גורם משמעותי הן בכך שמייד עם הקמת האוניברסיטה הוקם בה מכון למתמטיקה, והן בכך שהיתה זו מתמטיקה "טהורה". חוט משוך מכאן למסורת של הצטיינות במתמטיקה "טהורה" באוניברסיטה העברית ואח"כ באוניברסיטאות אחרות בארץ. (מסורת שניזונה ברובה מדורות של סטודנטים מצטיינים.)
לנדאו היה בן למשפחה יהודית אמידה ומכובדת מאוד בברלין. הוא התייחס על ר' יחזקאל הלוי לנדא מפראג, מראשי מנהיגי היהדות במאה ה-18, הידוע בכינוי "נודע ביהודה" על שם ספר השו"ת שחיבר. (וגם שמו העברי של אדמונד לנדאו היה יחזקאל.) מאידך, אשתו של אדמונד לנדאו היתה בתו של הביולוג המפורסם פאול אהרליך, שנחשב בדורו לראש המדענים הגרמנים-יהודים.
משנות ה-1920 הזדהה לנדאו יותר ויותר עם המסורת היהודית והציונות. הוא למד עברית. כאשר, בהשפעת חיים וייצמן, דובר על הקמת האוניברסיטה העברית בירושלים, היה לנדאו בין המדענים היהודים שתמכו בכך בהתלהבות (בין המתמטיקאים והפיסיקאים האחרים היו אלברט איינשטיין, ז'אק אדמר וטוליו לוי-צ'יויטה). אבל לנדאו הגדיל לעשות: הוא לא רק השתתף בטכס הפתיחה של האוניברסיטה ב-1925 ונשא שם הרצאה בעברית על "שאלות פתוחות וסתומות בתורת המספרים האלמנטרית" (אולי ההרצאה העברית הראשונה בכלל במתמטיקה "גבוהה"), אלא שמייד כאשר החלה האוניברסיטה לקבל סטודנטים, בסמסטר חורף 1927-28, בא לנדאו עם משפחתו לירושלים כפרופסור הבכיר שם למתמטיקה. על הלך רוחו של לנדאו בחצי-שנה זו תעיד העובדה שרבים ממכתביו מירושלים כתובים בעברית, מתוארכים בתאריך העברי וחתומים: "יחזקאל הלוי, ירושלים עיה"ק". למרות שבסוף סמסטר זה חזר לנדאו עם משפחתו לגטינגן, הוא המשיך להיות מעורב בתוכנית הלימודים והוא שקבע מי יהיו יורשיו: אברהם הלוי פרנקל ומיכאל פקטה, ש"מלכו" במכון שנים רבות.
באתר של האיגוד למתמטיקה בישראל $latex www.imu.org.il$ ניתן למצוא את ההרצאה של לנדאו בעברית שהוזכרה לעיל, וגם מאמר מתמטי שלו בעברית. יש שם גם מאמר באנגלית של שאול כץ הדן בהרחבה בהיסטוריה של לנדאו ותחילת מכון איינשטיין למתמטיקה באוניברסיטה העברית.
והנה, בספר שכתב ביברבך אחרי המלחמה, "תורת הבניות הגיאומטריות", שיצא לאור בבאזל ב-1925, הוא מסב את תשומת לב הקוראים להוכחה לכך שאי אפשר לחלק זווית כללית לשלושה ע"י סרגל ומחוגה, שגילה לנדאו כשהיה סטודנט בן 20 (ב-1897) ושלא היתה ידועה קודם לכן. היא נמצאה על דף נייר שכתב לנדאו ושנמצא בעזבונו של המתמטיקאי $latex H.~A.~Schwarz$. ביברבך משבח את לנדאו הצעיר על "יצירה עצמאית ראשונה של מתמטיקאי גדול".
האם ביברבך רצה לנסות להתנער (לפחות בעיני הציבור) מעברו הנאצי? נביא תרגום חפשי של מה שכתב לנדאו בדף הנייר:
"כדי להוכיח, שחלוקת זווית כללית לשלושה ע"י מספר סופי של בניות עם סרגל ומחוגה אינה אפשרית, צריך להראות, שאי אפשר, ע"י מספר סופי של פעולות רציונליות ( כלומר ארבע פעולות החשבון) והוצאות שורשים ריבועיים, לקבל מ $latex {a}$ ביטוי $latex {u}$ שיקיים את המשוואה
$latex \displaystyle f(u)\equiv 4u^3-3u+a=0 \ \ \ \ \ (1)$
שכן עבור $latex {x=\sin(\phi/3)}$ מתקיים $latex {\sin\phi=3x-4x^3}$, כלומר $latex {4x^3-3x+\sin\phi=0}$. [ראו מאמרו של גדי אלכסנדרוביץ' שהופיע בגיליון הקודם: בניות בסרגל ומחוגה. אילו הייתה לנו שיטה לחלק זווית כללית $latex {\phi}$ לשלושה בעזרת סרגל ומחוגה, היינו יכולים לצאת מקטע באורך $latex {\sin\phi}$ ולבנות קטע באורך $latex {\sin(\phi/3)}$].
נניח, איפוא, שקיים ביטוי כזה ב $latex {a}$. כדי ליצור אותו [נתמקד בשלבים בהם הוצאנו שורש ריבועי] יש לבנות סידרת ביטויים $latex {y_1,\ldots,y_s}$ , כאשר את $latex {y_i}$ קיבלנו מהוצאת שורש ריבועי, כלומר $latex {y_i^2}$ הוא ביטוי רציונלי ב $latex {a,y_1,\ldots,y_{i-1}}$ ו $latex {y_i}$ עצמו אינו כזה, בעוד ש $latex {x}$ הוא ביטוי רציונלי ב $latex {a,y_1,\ldots,y_s}$ ולא ב $latex {a,y_1,\ldots,y_{s-1}}$. נניח שלקחנו את מספר השלבים $latex {s}$ הקטן ביותר שנותן שורש כזה, ונניח ש $latex {s\ge1}$, כלומר שאין שורש למשוואה (1) שהוא ביטוי רציונלי ב $latex {a}$.
נזכיר ש $latex {y_s}$ הוא שורש ריבועי של ביטוי רציונלי ב $latex {a,y_1,\ldots,y_{s-1}}$. אז קל להיווכח ש $latex {x}$ ניתן לכתיבה בצורה $latex {x=\alpha+\beta y_s}$ כאשר $latex {\alpha}$ ו $latex {\beta}$ הם ביטויים רציונליים ב $latex {a,y_1,\dots,y_{s-1}}$. [ כי $latex {x}$ הוא ביטוי רציונלי ב $latex {a,y_1,\ldots,y_s}$, כלומר מנה של שני פולינומים ב $latex {y_s}$ עם מקדמים שהם ביטויים רציונליים ב $latex {a,y_1,\ldots,y_{s-1}}$, ו $latex {y_s}$ הוא שורש ריבועי של ביטוי כזה. לכן $latex {x}$ הוא מנה $latex {\dfrac{\alpha"+\beta"y_s}{\alpha'+\beta'y_s}}$ ומהמכנה ניפטר ע"י הכפלת מונה ומכנה בביטוי הצמוד $latex {\alpha'-\beta'y_s}$].
כאן $latex {\beta\ne0}$, אחרת היה $latex {x=\alpha}$ שהוא ביטוי רציונלי ב $latex {a,y_1,\ldots,y_{s-1}}$.
אבל אז גם $latex {\alpha-\beta y_s}$ חייב להיות שורש של $latex {f(u)=0}$. אכן, את
$latex \displaystyle f(\alpha+\beta y_s)=4(\alpha+\beta y_s)^3-3(\alpha+\beta y_s)+a$
אפשר לכתוב כ $latex {A+By_s}$, כאשר $latex {A}$ ו $latex {B}$ ביטויים רציונליים ב $latex {a,y_1,\ldots,y_{s-1}}$, ואז $latex {f(\alpha-\beta y_s)=A-By_s}$. הינחנו ש $latex {\alpha+\beta y_s}$ הוא שורש, כלומר $latex {A+By_s=0}$. אבל אז חייב להיות $latex {B=0}$, אחרת היינו מקבלים $latex {y_s=-A/B}$ , ביטוי רציונלי ב $latex {a,y_1,\ldots y_{s-1}}$. מכאן שגם $latex {f(\alpha-\beta y_s)=A-By_s=0}$.
מאחר ש $latex {\beta\ne0}$, השורשים $latex {\alpha+\beta y_s}$ ו $latex {\alpha-\beta y_s}$ שונים, וכיוון שמקדם $latex {u^2}$ ב $latex {f(u)}$ הוא $latex {0}$, סכום שלושת שורשי הפולינום הוא $latex {0}$ [ זיכרו שמקדמי פולינום (עם מקדם ראשי $latex {1}$) הם הפולינומים הסימטריים היסודיים בשורשיו] ומכאן שהשורש השלישי הוא $latex {-(\alpha+\beta y_s+\alpha-\beta y_s)=-2\alpha}$, שהוא ביטוי רציונלי ב $latex {a,y_1,\ldots y_{s-1}}$, בניגוד למינימליות של $latex {s}$.
הוכחנו, איפוא, שאם יש למשוואה שורש שהוא ביטוי ב $latex {a}$ שמתקבל ע"י פעולות רציונליות והוצאת שורשים ריבועיים, אזי יש לה שורש שמתקבל רק ע"י פעולות רציונליות, וידוע איך להוכיח שזה בלתי אפשרי" (את זה נשאיר כתרגיל).
[פיתרון: נוכיח שעבור $latex {a=1/2}$ (כלומר $latex {\phi=30^\circ}$) אין ביטוי כזה. אכן, אילו היה אפשר למצוא פיתרון $latex {u}$ למשוואה (1) ע"י פעולות רציונליות, היה זה שורש רציונלי $latex {u=p/q}$ בו $latex {p}$ ו $latex {q}$ שלמים וזרים. כלומר
$latex \displaystyle 0=f(u)=f\left(\frac{p}{q}\right)=4\frac{p^3}{q^3}-3\frac{p}{q}+a= 4\frac{p^3}{q^3}-3\frac{p}{q}+\frac12.$
נכפיל ב $latex {2q}$. נקבל $latex {8\frac{p^3}{q^2}=6p-q}$ ומכאן $latex {q^2|8p^3}$ ומאחר ש $latex {q}$ זר ל $latex {p}$, $latex {q^2|8}$ כלומר $latex {q=\pm1,\pm2}$ ואז $latex {u}$ שלם או חצי שלם. אבל אף $latex {u}$ כזה לא יכול לקיים $latex {f(u)=4u^3-3u+\frac12=0}$].
קו-אופי מיוחד של הוכחה זו (כפי שמציין ביברבך בספרו) הוא שהיא משתמשת בכך שלמשוואה ממעלה שלישית לא יכולים להיות יותר משלושה שורשים.

עמוד מתוך: $latex {L.~Bieberbach, Theorie~der~Geometrischen~Konstruktionen,Basel~1952}$
מה זה …0.999?
רון אהרוני
מה זה $latex {0.999\ldots}$
1. שווה, או שואף?
רבים מכם נתקלו בוודאי במספר $latex {0.999\ldots}$. אבל מה זה? יש כאלה שסבורים שזה פשוט $latex {1}$. יש כאלה שמוכנים להסכים לזה, ובכל זאת קצת מפקפקים, או אפילו מתרגזים על הרעיון שאותו מספר נכתב בשתי צורות. ויש כאלו שטוענים שזה לא $latex {1}$, אלא שזה שואף ל-$latex {1}$.
לפני שאמשיך, אנא בררו לעצמכם - מה דעתכם? שווה ל-$latex {1}$, או שואף ל-$latex {1}$?
כדי לא להשאיר אתכם במתח, אומר לכם כבר עתה - המספר הזה שווה ל-1. $latex {0.999\ldots=1}$. אבל צריך להסביר למ הכוונה. מי שמתרגז על זה שאותו מספר נכתב בשתי צורות - אנא התאזרו בסבלנות.
2. מהו פיתוח מספר עשרוני אינסופי?
מדי שנה, ב-$latex {14}$ במרץ, חוגג עולם המתמטיקה את יום ה-$latex {\pi}$. באמריקה כותבים את התאריך $latex {3.14}$ - ההתחלה המפורסמת של הפיתוח העשרוני של $latex {\pi}$. הנה ההמשך, $latex {100}$ הספרות הראשונות:
$latex \displaystyle \pi = 3.141592653589793238462643383279502884197169399375105820974944592307816406286\ldots$
שלוש הנקודות משמען שצריך להמשיך. אבל מה פירוש שצריך להמשיך? הפירוש הוא זה: המספרים
$latex \displaystyle 3, 3.1,~ 3.14,~ 3.141,~ 3.1415,~ 3.14159,~ 3.141592, \ldots,$
הולכים ומתקרבים לערך האמיתי של $latex {\pi}$, כלומר ליחס בין היקף מעגל לקוטר שלו. כל איבר בסדרה הוא קירוב יותר טוב לערך האמיתי. וכמובן - כל איבר בסדר קטן מן הערך האמיתי של $latex {\pi}$. הרי כדי להתקרב ל-$latex {\pi}$ מוסיפים עוד ועוד. אלו הם קירובים מלמטה.
בלשון מדויקת אומרים שסדרת המספרים האלה שואפת ל-$latex {\pi}$. במינוח אחר, הגבול שלה הוא $latex {\pi}$.
זהו המובן של פיתוח עשרוני אינסופי של מספר: סדרת המספרים המתקבלת מכך שעוצרים במקום סופי אחרי הנקודה שואפת למספר.
אם כן, העובדה ש-$latex {0.999\ldots=1}$ משמעה הוא שסדרת המספרים $latex {0,~0.9, ~0.99,~0.999, \ldots}$ שואפת ל-$latex {1}$. הגבול שלה הוא $latex {1}$. ואכן, הסתכלו על המרחק של המספרים האלה מ-$latex {1}$: המרחק של $latex {0}$ מ-$latex {1}$ הוא $latex {1}$; המרחק של $latex {0.9}$ מ-$latex {1}$ הוא $latex {0.1}$; המרחק של $latex {0.9}$ מ-$latex {1}$ הוא $latex {0.1}$; המרחק של $latex {0.99}$ מ-$latex {1}$ הוא $latex {0.01}$; המרחק של $latex {0.999}$ מ-$latex {1}$ הוא $latex {0.001}$. המרחקים הולכים וקטנים, והם שואפים ל-$latex {0}$. זהו משמעו שסדרת המספרים שואפת ל-$latex {1}$.
מי שמרגיש נוח עם ביטויים אלגבריים, יכול לכתוב זאת כך: מרחקו של האיבר ה-$latex {n}$ בסדרה מ-$latex {1}$ הוא $latex {\frac{1}{10^n}}$ (ההנחה היא שמתחילים לספור מ-$latex {0}$! האיבר מספר $latex {0}$ בסדרה הוא $latex {0}$, האיבר מספר $latex {1}$ הוא $latex {0.9}$, האיבר מספר 2 הוא $latex {0.99}$ וכו'). והמספרים $latex {\frac{1}{10^n}}$ שואפים ל-$latex {0}$.
כאשר תלמדו "לראשונה" על גבול של סדרות של מספרים תוכלו לומר לעצמכם - אנחנו כבר מכירים את המושג הזה, מפיתוח עשרוני אינסופי של מספרים עשרוניים!
אם כן, מדוע אי אפשר לומר ש-$latex {0.999\ldots}$ שואף ל-$latex {1}$? משום שהמספר $latex {0.999\ldots}$ כבר משמעו "גבול". לומר ש- "$latex {0.999\ldots}$ שואף ל-$latex {1}$" זה כמו להגיד "הגבול של הסדרה שואף ל-$latex {1}$", כאשר המינוח המדויק הוא "הגבול שווה ל-1". לומר "הגבול שואף" הוא לומר פעמיים אותו דבר - הגבול הוא מספר ששואפים אליו.
3. שברים עשרוניים מחזוריים
מכך ש-$latex {0.999\ldots=1}$ קל לדעת מהו $latex {0.333\ldots}$. בכל מקום שבו יש $latex {9}$ מופיע עכשיו $latex {3}$. במספר $latex {0.999\ldots}$ יש $latex {9}$ עשיריות )במקום של העשירות, הכוונה(; במספר $latex {0.333\ldots}$ יש $latex {3}$ עשיריות. במספר $latex {0.999\ldots}$ יש $latex {9}$ מאיות; במספר $latex {0.333\ldots}$ יש $latex {3}$ מאיות, וכו'. כל פעם ש-$latex {0.999\ldots}$ "אוסף" משהו, $latex {0.333\ldots}$ אוסף פי 3 פחות. אם כן $latex {0.333\ldots}$ קטן פי $latex {3}$ מ-$latex {0.999\ldots}$, כלומר מ-$latex {1}$, ולכן הוא שווה ל-$latex {\frac{1}{3}}$.
אני משער שלא חידשתי לכם כלום: $latex {0.333\ldots}$ הוא שבר מפורסם!
באותה צורה אפשר לראות ש-$latex {0.111\ldots}$ קטן פי $latex {9}$ מ-$latex {0.999\ldots}$, ולכן
$latex {0.111\ldots=\frac{1}{9}}$, ו-$latex {0.222\ldots=\frac{2}{9}}$.
למעשה, כל מספר עשרוני מחזורי אפשר להפוך כך לשבר. נתבונן למשל במספר $latex {0.121212…}$ הוא נקרא מחזורי משום שממקום מסוים ואילך הוא חוזר על עצמו. השוו אותו עם המספר $latex {0.999\ldots}$.
שתי הספרות הראשונות ב-$latex {0.121212…}$ מציינות $latex {12}$ מאיות. שתי הספרות הראשונות ב- $latex {0.999\ldots}$, לעומת זאת, הן $latex {99}$ מאיות, פי ב-$latex {0.121212…}$ מציינות $latex {12}$ מאיות, פי $latex {\frac{99}{12}}$ יותר.
שתי הספרות הבאות ב-$latex {0.121212…}$ מציינות $latex {12}$ חלקי עשרת אלפים. שתי הספרות הראשונות ב- $latex {0.999\ldots}$, לעומת זאת, הן $latex {99}$ חלקי עשרת אלפים, פי ב-$latex {0.121212…}$ מציינות $latex {12}$ מאיות, פי $latex {\frac{99}{12}}$ יותר.
כך זה ממשיך. כל פעם שהמספר $latex {0.121212…}$ "מקבל" משהו, המספר $latex {0.999\ldots}$ מקבל פי $latex {\frac{99}{12}}$ יותר. אם שני אנשים צוברים רכוש, וכל פעם שהראשון מקבל סכום השני מקבל סכום גדול פי $latex {\frac{99}{12}}$, השני יצבור בסופו של דבר פי $latex {\frac{99}{12}}$ יותר מן הראשון. כלומר $latex {0.999\ldots}$ גדול פי $latex {\frac{99}{12}}$ מ-$latex {0.121212…}$. במילים אחרות, $latex {0.121212…}$ קטן פי $latex {\frac{99}{12}}$ מ-$latex {0.999\ldots}$, כלומר מ-$latex {1}$. אם כן, $latex {0.121212…= \frac{12}{99}}$.
בדומה, $latex {0.127127127…= \frac{127}{999}}$. האם תוכלו להסביר מדוע?
4. גם ההפך נכון - הייצוג העשרוני של כל שבר הוא מחזורי
ראינו שכל שבר עשרוני מחזורי ניתן לביטוי כשבר. האם גם ההפך נכון? האם הייצוג העשרוני של כל שבר הוא מחזורי? התשובה היא "כן". הדבר נובע מן הצורה שבה הופכים שבר לשבר עשרוני. יודעים איך עושים זאת? פשוט מחלקים חילוק ארוך. וכשבחילוק הארוך חוזרים לאותה שארית, הפיתוח מתחיל לחזור על עצמו.
למשל, כדי לחשב מהו $latex {\frac{1}{7}}$ מחלקים $latex {1}$ ב-$latex {7}$. כמובן, יוצא $latex {0}$, עם שארית $latex {1}$, כלומר $latex {10}$ עשיריות. $latex {10}$ עשיריות לחלק ל-$latex {7}$ הן $latex {1}$, עם שארית $latex {3}$, שהן $latex {30}$ מאיות. $latex {30}$ מאיות לחלק ל-$latex {7}$ הן $latex {4}$ עם שארית $latex {2}$, שהן $latex {20}$ אלפיות. $latex {20}$ אלפיות לחלק ל-$latex {7}$ הן $latex {2}$ עם שארית של $latex {6}$, שהן $latex {60}$ חלקי עשרת אלפים. $latex {60}$ חלקי עשרת אלפים לחלק ל-$latex {7}$ הן $latex {8}$ עם שארית של $latex {4}$, שהן $latex {40}$ חלקי מאה אלף; $latex {40:7=5(5)}$ כלומר שארית של $latex {50}$ חלקי מיליון, $latex {50:7=7(1)}$ ומן הרגע שחזרנו לשארית $latex {1}$ אנחנו מתחילים לחזור על עצמנו. אם כן $latex {\frac{1}{7}=0.142857142857142857\ldots}$.
שימו לב - אחרי $latex {6}$ ספרות התחלנו לחזור על עצמנו. אחד פחות מ-$latex {7}$. האם זה מקרה? לא ממש. המחזור לא יכול להיות ארוך מ-$latex {6}$, כי יש רק $latex {6}$ שאריות אפשריות מ-$latex {7}$ - $latex {1,~2,~3,~4,~5,~6}$ (כל המספרים הקטנים מ-$latex {7}$. מדוע לא תיתכן שארית $latex {0}$? בסוף המאמר יש שאלה שמדריכה לכך.) מדוע בדיוק $latex {6}$? זוהי כבר שאלה יותר קשה, שאולי נחזור אליה באחד המאמרים הבאים. נסו: מהו אורך המחזור בפיתוח של $latex {\frac{1}{11}}$? בפיתוח של $latex {\frac{1}{13}}$?
5. האם כל שבר אפשר לכתוב עם מכנה שכולו תשיעיות?
בואו נחזור ל-$latex {\frac{1}{7}}$. ראינו שהוא שווה ל-$latex {0.142857142857142857\ldots}$ לפי הסעיף הקודם, יוצא ש-$latex {\frac{1}{7}=\frac{142857}{999999}}$.
האם זה נכון לכל שבר? לאו דווקא. הסתכלו המחזורי $latex {0.7121212\ldots}$. גם הוא נחשב למחזורי. הוא שווה ל-$latex {\frac{7}{10}+\frac{12}{990}}$ (מדוע?), שהוא $latex {\frac{7\times 99+12}{90}}$.
בעיה מספר 1- הוכיחו שכל שבר אפשר לכתוב עם מכנה מן הצורה $latex {999\ldots900\ldots0}$ - מספר שיש בו רק תשיעיות ולאחריהן אפסים.
מוזר, לא?
בעיה מספר 2- האם תוכלו להוכיח את העובדה שמופיעה בבעיה הקודמת גם ישירות?
שימו לב: משמעות הדבר היא שלכל מספר יש כפולה מן הצורה $latex {999\dots900\ldots0}$ - מספר שיש בו רק תשיעיות ואחריהן אפסים. מוזר, לא? בבעיה אתם מתבקשים לתת לעובדה הזאת הוכחה ישירה.
6. עוד שתי שאלות
בעיה מספר 3- מה מאפיין שברים שיש להם ייצוג עשרוני סופי? איזה סוג של מכנה צריך להיות לשבר כזה?
בעיה מספר 4- שאלה למחשבה: מה לדעתכם יש יותר - מספרים שבהם יש מחזוריות, או מספרים שאין בהם מחזוריות? כלומר מה יש יותר - מספרים שהם שברים אומספרים שאינם שברים?
אני חושב שאתם יכולים לנחש את השתובה. באחד הגיליונות הבאים נסביר מדוע הניחוש הזה (אני מקווה שניחשתם נכון) הוא מוצדק.
7. ומה הלאה?
בגיליון הבא נקשר את כל מה שלמדנו למושג שנקרא "סדרות גיאומטריות". ליתר דיוק, סדרות גיאומטריות אינסופיות.
חידות - גיליון 2
אסף שפירא
חידות מגיליון פברואר שעדיין לא נפתרו (1,2,4,6,9,10) בהתאמה:
- אדם בגובה נתון עומד זקוף מול מראה במימדים נתונים. באיזה מרחק עליו לעמוד, על מנת שיוכל לראות במראה את כפות הרגליים?
- רון משחק בשלושה מטבעות שמונחים על השולחן. בכל שלב הוא מותח שער דמיוני בין שניים מהמטבעות, ומעביר דרכו את המטבע השלישי. האם יוכל בשבעה צעדים בדיוק להחזיר כל מטבע למקומו המקורי?
- כעת משחקים שני השחקנים במשחק אחר — בתחילה אין על לוח השחמט אבני דומינו, והשחקן הראשון בוחר במשבצת. על השחקן השני לכסות את המשבצת שאותה בחר השחקן הראשון באבן דומינו, יחד עם אחת מהמשבצות הסמוכות לה. בשלב הבא על השחקן הראשון לבחור משבצת נוספת שעוד לא כוסתה באבן דומינו, ועל השחקן השני לכסות גם אותה. כך ממשיך המשחק, עד שלאחד השחקנים אין מהלך חוקי — או שמגיע תור השחקן הראשון והלוח מלא, או שהגיע תורו של השחקן השני, וכל המשבצות שסמוכות לזו שבחר הראשון כבר מכוסות. השחקן שלא יכול לשחק הוא המפסיד. איזה מבין שני השחקנים יכול להבטיח את נצחונו במשחק זה?
- נסתכל על קבוצות של מספרים בין $latex {1}$ ל-$latex {n}$ בעלות ממוצע שלם. עבור $latex {n}$ זוגי, האם מספר הקבוצות האלה זוגי או אי-זוגי?
- נתון משולש $latex {ABC}$, ושלוש נקודות על צלעותיו — $latex {D}$ על הצלע $latex {AB}$, $latex {E}$ על הצלע $latex {BC}$ ו$latex {F}$ על הצלע $latex {AC}$. המשולש $latex {DEF}$ הוא משולש שווה צלעות, ואורכי הקטעים $latex {AD}$, $latex {BE}$ ו$latex {CF}$ שווים זה לזה. הוכיחו ש$latex {ABC}$ גם הוא משולש שווה צלעות.
- ניב ואורה משחקים במשחק. בכל סיבוב על שניהם לנחש תוצאת הטלה של מטבע הוגן, אחרי כן מטילים את המטבע, וניב ואורה מקבלים נקודה אם שני הניחושים היו נכונים. כך המשחק נמשך, כאשר ניב ואורה יודעים בסוף כל סיבוב מה כל אחד ניחש ומה היתה תוצאת ההטלה, אך אין להם יכולת לתקשר זה עם זה מרגע שהמשחק החל. ניב יכול להסתמך בניחושים שלו רק על מה שלמד בסיבובים הקודמים, בהתאם לסיכום שעשה עם אורה לפני תחילת המשחק. לאורה, לעומת זאת, יש יכולת ניבואית — רגע לפני שהמשחק מתחיל היא יכולה לגלות את כל תוצאות ההטלות שיתקבלו. לפני המשחק, כאשר אורה וניב מתאמים כיצד לפעול, הם יודעים על יכולתה הניבואית של אורה, אבל היא עוד לא יכולה לגלות את תוצאות ההטלות העתידיות. נסו להציע אסטרטגיה, שבה מספר הנקודות הממוצע שיקבלו ניב ואורה אחרי מספר רב של מהלכים יהיה כמה שיותר גדול.
חידות נוספות לגליון מרץ:
- כדי להרכיב שרשרת, ניתן להשתמש בחרוזים אדומים, ירוקים ולבנים שמסודרים במעגל. כמה שרשראות באורך של שבעה חרוזים ניתן להרכיב? שימו לב לא לספור פעמיים שרשראות שנבדלות זו מזו רק בסיבוב.
- לשלושה מספרים $latex {a,b,c}$, הראו שאם $latex {a+b+c}$ מתחלק ב $latex {6}$ גם $latex {a^{3}+b^{3}+c^{3}}$ מתחלק ב $latex {6}$.
- מטילים קוביה הוגנת עד שסכום תוצאות ההטלה גדול או שווה $latex {n}$ . מה הסיכוי שסכום ההטלות בסוף שווה בדיוק ל $latex {n}$ , בגבול שבו $latex {n}$ מאוד גדול?
- נתונים שני מספרים אי רציונלים חיוביים $latex {\alpha}$ ו $latex {\beta}$ , כך ש $latex {\frac{1}{\alpha}+\frac{1}{\beta}=1}$ . נסתכל על הערך השלם התחתון של הכפולות הטבעיות של $latex {\alpha}$ ושל $latex {\beta}$ , כלומר המספרים מהצורה $latex {\left\lfloor n\cdot\alpha\right\rfloor }$ ו $latex {\left\lfloor n\cdot\beta\right\rfloor }$ , ל $latex {n}$ טבעי. הראו כי בצורה זו מתקבלים כל המספרים הטבעיים, וכל אחד מהם מתקבל פעם אחת בלבד.
פתרונות לגיליון פברואר, ברכות לעמרי שמחי שפתר נכון את שאלה 5:
- השחקן השני יכול להבטיח את נצחונו. לכל מהלך של השחקן הראשון, השחקן השני יגיב במהלך סימטרי — הוא יסתכל על שתי המשבצות שמילא השחקן הראשון, וימלא את שתי המשבצות שנמצאות במרחק שווה ממרכז הלוח ובכיוון ההפוך. היות שאין חפיפה בין שתי משבצות סמוכות לשתי המשבצות הסימטריות, והלוח נשאר סימטרי אחרי כל מהלך של השחקן השני, תמיד השחקן השני יוכל להניח אבן דומינו, וכך מובטח שינצח.
- קודם כל, נשים לב שמתקיים $latex {x\left(1-x\right)\le\frac{1}{4}}$ : הפונקציה $latex {f\left(x\right)=x\left(1-x\right)}$ היא פרבולה עם נקודת מקסימום ב $latex {\frac{1}{2}}$ שבה מתקבל הערך $latex {\frac{1}{4}}$ . לכן גם $latex {y\left(1-y\right)}$ ו $latex {z\left(1-z\right)}$ קטנים או שווים $latex {\frac{1}{4}}$ . אם כך, מכפלת שלושת המספרים:
$latex \displaystyle x\left(1-y\right)\cdot y\left(1-z\right)\cdot z\left(1-x\right)=x\left(1-x\right)\cdot y\left(1-y\right)\cdot z\left(1-z\right)\le\frac{1}{4}\cdot\frac{1}{4}\cdot\frac{1}{4}, $
לכן הממוצע ההנדסי שלהם קטן או שווה $latex {\frac{1}{4}}$ , ואם כך לפחות אחד מהם קטן או שווה $latex {\frac{1}{4}}$.
-
התשובה היא $latex {33}$. נסתכל על $latex {m}$ מספרים בין $latex {1}$ ל $latex {2013}$ , ונסדר אותם בסדר עולה $latex {x_{1}\le x_{2}\le\dots\le x_{m}}$ . אם שלושה מספרים הם צלעות של משולש חד זווית, יהיו שלושה מספרים כאלה עם אינדקסים עוקבים — אם מקטינים במשולש ישר זווית את הצלע הגדולה )כך שתישאר הצלע הגדולה( ומגדילים את הצלע הקטנה )כך שתישאר הצלע הקטנה( הוא נשאר משולש חד זווית. התנאי על המספרים $latex {x_{i},x_{i+1},x_{i+2}}$ שיהיו צלעות של משולש שאינו חד זווית הוא $latex {x_{i}^{2}+x_{i+1}^{2}\le x_{i+2}^{2}}$ — הצלע הגדולה גדולה לפחות כמו יתר של משולש ישר זווית מתאים. לכן כדי שלא יהיו שלושה מספרים שהם צלעות של משולש חד זווית, הסדרה $latex {x_{1}^{2},x_{2}^{2},\dots,x_{m}^{2}}$ צריכה להיות גדולה מסדרת פיבונאצ’י $latex {F_{n}}$ . אבל המספר האחרון $latex {x_{m}^{2}\le2013^{2}}$ , והיות ש $latex {F_{33}<2013^{2}}$ ו $latex {F_{34}>2013^{2}}$ , אם $latex {m>33}$ הסדרה לא יכולה להיות גדולה מסדרת פיבונאצ’י, וחייבים להיות שלושה מספרים שהם צלעותיו של משולש חד זווית.
-
נראה שקיים $latex {\alpha}$ , כך שלכל פולינום $latex {p\left(x\right)=a_{0}+a_{1}x+\dots+a_{100}x^{100}}$ מתקיים $latex {|a_{0}|+|a_{1}|+\dots+|a_{100}|\le\alpha\int_{0}^{1}|p\left(x\right)|\mbox{d}x}$ . היות ש $latex {p\left(0\right)=a_{0}}$ , ודאי יתקיים גם $latex {|p\left(0\right)|\le\alpha\int_{0}^{1}|p\left(x\right)|\mbox{d}x}$ . בגלל הערך המוחלט, ניתן להניח בלי הגבלת הכלליות ש $latex {a_{0}\ge0}$ )אחרת, נהפוך את כל המקדמים ונקבל אותה תוצאה(. אם כך, נסתכל על הפולינומים שעבורם $latex {|a_{0}|+|a_{1}|+\dots+|a_{100}|=1}$ , ונמצא את הפולימום שעבורו $latex {\int_{0}^{1}|p\left(x\right)|\mbox{d}x}$ מינימלי. ניתן למצוא את מקדמיו כמינימום של הפונקציה:
$latex \displaystyle g\left(a_{1},\dots,a_{100}\right)=\int_{0}^{1}|\left(1-|a_{1}|-\dots-|a_{100}|\right)+a_{1}x+\dots+a_{100}x^{100}|\mbox{d}x, $
כשכל המשתנים חסומים בין $latex {-1}$ ל $latex {1}$ . נסמן אותו ב $latex {q\left(x\right)=b_{0}+b_{1}x+\dots+b_{100}x^{100}}$ , ונבחר $latex {\alpha=\frac{1}{\int_{0}^{1}|q\left(x\right)|\mbox{d}x}}$ . אז לכל פולימום $latex {p\left(x\right)=a_{0}+a_{1}x+\dots+a_{100}x^{100}}$ )בלי הגבלה על המקדמים(, לפולינום $latex {\frac{p\left(x\right)}{|a_{0}|+|a_{1}|+\dots+|a_{100}|}}$ מקדמים שסכום הערכים המוחלטים שלהם הוא $latex {1}$ , לכן:
$latex \displaystyle \int_{0}^{1}|\frac{p\left(x\right)}{|a_{0}|+|a_{1}|+\dots+|a_{100}|}|\mbox{d}x\ge\int_{0}^{1}|q\left(x\right)|\mbox{d}x=\frac{1}{\alpha}, $
וזה אומר ש $latex {|a_{0}|+|a_{1}|+\dots+|a_{100}|\le\alpha\int_{0}^{1}|p\left(x\right)|\mbox{d}x}$ , כמו שרצינו.
חידות לילדים
קוונט - תרגום : אלכס קמרסקי
- במשחקים האולימפיים הספורטאים מהנבחרת הלאומית זכו ב-96 מדליות בסה”כ, מתוכם 65 מדליות זהב וארד, ו-61 מדליות זהב וכסף. בכמה מדליות זהב, בכמה מדליות כסף ובכמה מדליות ארד הם זכו?
- האם אפשר למצוא שני אבות ושני בנים שאפשר לחלק ביניהם 3 תפוחי-עץ כך שכל אחד יקבל בדיוק תפוח אחד?
- ביום הולדת שלו אלכס הביא לכיתה חבילת סוכריות. כמה סוכריות יש לך? – שאלו אותו הילדים בכיתה. אני זוכר – ענה להם אלכס – שכשסידרתי אותם בזוגות, בשלשות, וברביעיות, כל פעם נשארה לי סוכריה אחת, וכשסידרתי אותם בחמישיות, לא נשארה לי אף סוכריה. כמה סוכריות הביא אלכס?
- בחדר שלושה כדורים בשלושה צבעים שונים: לבן, שחור וירוק. את הכדורים הניחו בשלוש קופסאות – כדור אחד בכל קופסא. על כל אחת מהקופסאות הדביקו מדבקה. על הראשונה רשמו: “לבן”, על השניה רשמו: “שחור” ועל השלישית רשמו: “לבן או ירוק”. אף מדבקה לא תואמת באמת את מה שהיא מכילה. מהם הצבעים של הכדורים בכל אחת מהקופסאות?
- סוהר מודיע למאה אסירים שלמחרת ישים לכל אחד מהם כובע על ראשו, בצבע שחור או לבן. כל אחד מהם יכול לראות את הכובע של חבריו, אבל לא את שלו. כל אחד מהם צריך לנחש את הצבע של כובעו. אם לפחות 50 מהם יצדקו, ישתחררו כולם. אם פחות מ-50 יצדקו, יישארו כולם לנצח בבית הסוהר. האסירים רשאים לקבוע אסטרטגיה לניחוש, לפני שהם מנחשים. כיצד יצליחו להשיג את מטרתם?
[*] שאלות 1-4 מתוך העיתון ברוסית "קוונט" , תרגום: אלכס קמרסקי. עריכה: מיכאל אנטוב. שאלה 5 - רון אהרוני