נטגר גליון 20
דבר העורך
רון אהרוני
אחד הדברים היפים במתמטיקה הוא חיבור של תחומים שונים. בגיליון הנוכחי יש לנו דוגמה יפה לכך - פתרון בעיה קומבינטורית בעזרת טורי חזקות. הרעיון המקורי היה של אוילר, והוא נקרא "פונקציות יוצרות". פרופ' רוס פינסקי מן הטכניון הסכים לכתוב מאמר על הנושא - אנחנו מקווים שתיהנו, וכמו כן אנחנו מקווים להוסיף מאמרי המשך בנושא בעתיד.
אנה ליזהטוב תרמה גם היא מאמר, על אחד מתחומי המתמטיקה החידתיים ביותר, הלוגיקה המתמטית. זוהי המתמטיקה של המתמטיקה, כלומר חקר מתמטי של החקירה המתמטית. מעניין, לא? ובמיוחד מעניין מה כבר אפשר לומר בנושא. מתברר שיש הרבה מאוד מה לומר.
ויש לנו גם ראיון עם מתמטיקאי - מן הדמויות המוכרות והצבעוניות ביותר בעולם המתמטי של ימינו - מתמטיקאי ישראלי המתגורר בארצות הברית, דורון ציילברגר. לדורון יש דעות נחרצות ומקוריות על "מה זו מתמטיקה", ולאן מועדות פניה של
המתמטיקה.
בברכת הנאה,
העורך.
חישוב מספרי Fibonacci בעזרת פונקציות יוצרות
רוס פינסקי
1 ההגדרה של סדרת פיבונצ׳י
סדרת פיבונצ'י $latex \{f_n\}_{n=0}^\infty$ היא אחת הסדרות המפורסמות ביותר במתמטיקה. מגדירים $latex f_0=0$ ו-$latex f_1=1$, ואז עבור $latex n\ge2$, מגדירים את הסדרה לפי נוסחת נסיגה:
$latex \displaystyle (1) \quad f_n=f_{n-1}+f_{n-2}$
במילים, כל איבר מתקבל כסכום שני קודמיו. לכן, למשל, $latex f_2=f_1+f_0=1+0=1$, $latex f_3=f_2+f_1=1+1=2$.
שלושה עשר המספרים הראשונים בסדרת פיבונצ'י הם:
$latex \displaystyle 0,1,1,2,3,5,8,13,21,34,55,89,144$
2 פונקציות יוצרות
במאמר הזה נמצא נוסחה מפורשת לאיבר הכללי $latex f_n$ בסדרת פיבונצ'י. למטרה זו ננצל כלי הנקרא פונקציות יוצרות. אבל תחילה, עלינו להזכיר מספר עובדות בנוגע לטור גיאומטרי.
נתבונן בטור
$latex \displaystyle \sum_{n=0}^\infty y^n=1+y+y^2+\cdots$
כאשר $latex y$ הוא מספר ממשי. טור נקרא גיאומטרי כאשר היחס בין כל איבר לקודמו הוא קבוע, ואכן כך אצלנו: $latex \frac{y^{n+1}}{y^n}=y$ לכל $latex n$. נסמן
$latex \displaystyle S_n=\sum_{i=0}^ny^i=1+y+y^2+\cdots +y^n$
מתקיים $latex yS_n=y(1+y+\cdots+y^n)=y+y^2+\cdots+y^{n+1}$. לכן,
$latex \displaystyle (1-y)S_n=S_n-yS_n=1-y^{n+1}$
אם $latex y\neq1$, נוכל לחלק ומתקבל $latex S_n=\frac{1-y^{n+1}}{1-y}$. אם $latex |y| \lt 1$, אז כש- $latex n$ שואף ל-$latex \infty$, $latex y^{n+1}$ שואף ל-0, ואנו מגיעים למסקנה כי אם $latex |y| \lt 1$ אז
$latex \displaystyle (2) \quad \sum_{n=0}^\infty y^n=\lim_{n\to\infty} S_n=\lim_{n\to\infty}\frac{1-y^{n+1}}{1-y}=\frac1{1-y}$
אבל אם $latex y>1$, אז כש- $latex n$ שואף ל-$latex \infty$, $latex y^{n+1}$ שואף ל-$latex \infty$, ואנו מגיעים למסקנה כי
$latex \displaystyle \sum_{n=0}^\infty y^n=\lim_{n\to\infty} S_n=\lim_{n\to\infty}\frac{y^{n+1}-1}{y-1}=\infty$
אם $latex y=1$, ברור ש- $latex \sum_{n=0}^\infty y^n=\infty$. הקורא יכול לחקור את המקרה ש- $latex y \lt -1$; לא נצטרך את המקרה הזה כאן. כעת נציג את הכלי של פונקציות יוצרות. אנו בונים פונקציה $latex F(x)$ לפי הנוסחה
$latex \displaystyle (3) \quad F(x)=\sum_{n=0}^\infty f_nx^n$
כאשר $latex \{f_n\}_{n=0}^\infty$ היא סדרת פיבונצ'י. טור כזה נקרא טור חזקות. מכיוון ש- $latex f_0=0$, מתקיים $latex F(x)=\sum_{n=0}^\infty f_nx^n=\sum_{n=1}^\infty f_nx^n$. שימו לב כי הטור שמגדיר את $latex F(x)$ אינו טור גיאומטרי; אכן היחס בין האיבר ה- $latex n$-י לאיבר ה-$latex (n+1)$-י בו הוא $latex \frac{f_{n+1}}{f_n}x=\frac{f_{n+1}x^{n+1}}{f_n x^n}$, וזה תלוי ב- $latex n$, כלומר אינו מספר קבוע.
3 פרק לפדנטים שבינינו - מדוע טור החזקות מתכנס
אנחנו נרצה לפעול על טור החזקות שבנוסחה (3), ואת הפעולות האלה צריך להצדיק. מתמטיקה, אחרי הכל, היא מקצוע מדויק!
ברור שהפונקציה $latex x^n$ עולה עבור $latex x\ge0$; כלומר אם $latex x_2\gt x_1 \ge 0$,אז מתקיים $latex x_2^n>x_1^n$. לכן גם $latex F(x)$ היא פונקציה עולה עבור $latex x\ge0$ (כיוון ש- $latex f_n>0$ לכל $latex n$.) בפרט, אם $latex F(x_0)=\infty$, עבור איזה $latex x_0>0$, אז בהכרח $latex F(x)=\infty$ עבור כל $latex x \gt x_0$. או באופן שקול, אם $latex F(x_1) \lt \infty$, עבור איזה $latex x_1 \gt 0$, אז בהכרח $latex F(x) \lt \infty$, עבור כל $latex x$ המקיים $latex 0 \le x \lt x_1$. מזה נובע שאחת משלוש האפשריות הבאות בתוקף:
(1) קיים $latex R\ge0$ כך ש- $latex F(x) \lt \infty$, עבור $latex 0 \le x \lt R$, ו- $latex F(x)=\infty$, עבור $latex x \gt R$ (לא נדבר כאן מה קורה עבור $latex x=R$);
(2) $latex F(x)=\infty$ עבור כל $latex x \gt 0$;
(3) $latex F(x) \lt \infty$ עבור כל $latex x\ge0$.
במקרה הראשון אנו מגדירים $latex R=0$ ובמקרה השלישי $latex R=\infty$. המספר $latex R$ נקרא רדיוס ההתכנסות של טור החזקות. (אם $latex F(x) \lt \infty$, אנו אומרים שהטור מתכנס עבור ה- $latex x$ הזה, ואם $latex F(x)=\infty$, אומרים שהטור מתבדר עבור ה- $latex x$ הזה.) חשוב לציין שכל הנ"ל נוגע למקרה שבו איברי הטור חיוביים; אחרת הסיפור יותר מסובך.
תפקידנו הראשון הוא להראות ש- $latex R \gt 0$; אחרת כל הפעולות האלגבריות שנפעיל בהמשך תהיינה חסרות משמעות. (יש טורים עם $latex R=0$; כלומר טורים שאינם מתכנסים עבור אף $latex x \gt 0$; למשל $latex \sum_{n=1}^\infty n!x^n$.) בשלב הזה, נעשה חישוב גס כדי להראות ש- $latex R \gt 0$. (עד תום המאמר נקבל את $latex R$ במדויק.) הסדרה $latex \{f_n\}_{n=0}^\infty$ עולה; כלומר $latex f_{n+1} \gt f_n$ לכל $latex n$. (זה נראה מובן מאליו ואפשר להוכיח אותו באינדוקציה). אז $latex f_n=f_{n-1}+f_{n-2} \lt 2f_{n-1}$. לאור זה, איברי הסדרה $latex \{g_n\}_{n=0}^\infty$, המקיימת $latex g_0=0$, $latex g_1=1$, ו- $latex g_n=2g_{n-1}$, עבור $latex n\ge2$, הם גדולים מאיברי הסדרה המקורית $latex \{f_n\}_{n=0}^\infty$; כלומר, $latex g_n\ge f_n$, לכל $latex n\ge0$. (נסו להוכיח את זה באינדוקציה: מתקיים $latex g_0\ge f_0$ ו- $latex g_1\ge f_1$; כעת נניח ש- $latex g_n\ge f_n$ ובעזרת הנחה זו וההגדרות של הטורים ($latex f_n=f_{n-1}+f_{n-2},\ g_n=2g_{n-1}$), הוכיחו כי $latex g_{n+1}\ge f_{n+1}$.)
מכיוון ש- $latex g_n\ge f_n\ge0$, על פי השוואה נובע שאם $latex \sum_{n=1}^\infty g_nx^n \lt \infty$, עבור איזה $latex x \gt 0$, אז בהכרח $latex \sum_{n=0}^\infty f_nx^n \lt \infty$ עבור אותו $latex x$. הסדרה $latex \{g_n\}_{n=1}^\infty$ פשוטה לחישוב: $latex \ g_3=2g_2=2^2\ ,g_2=2g_1=2 $ ובאופן כללי $latex g_n=2^{n-1}=\frac12 2^n$, עבור $latex n\ge1$. לכן מתקיים
$latex \displaystyle \sum_{n=0}^\infty g_nx^n=\sum_{n=1}^\infty g_nx^n=\sum_{n=1}^\infty \frac122^nx^n=\frac12\sum_{n=1}^\infty (2x)^n$
אבל זה טור גיאומטרי! לכן הטור מתכנס אם $latex |2x| \lt 1$, ואז בפרט עבור $latex 0 \le x \lt \frac12$. לכן, על פי השוואה, הטור שלנו גם הוא מתכנס עבור $latex 0 \le x \lt \frac12$. אז הוכחנו ש- $latex R\ge\frac12$; כלומר ש- $latex F(x) \lt \infty$ לפחות עבור $latex 0\le x \lt \frac12$.
4 ועכשיו לעיקר - איך מקבלים נוסחה למספרי פיבונצ'י מן הפונקציה היוצרת שלהם?
כעת נבצע כמה פעולות אלגבריות פשוטות שתובלנה לנוסחה מפורשת ל- $latex F$ (במקום במונחים של טור אינסופי). נכפול ב- $latex x^n$ בשני צדדי (1):
$latex \displaystyle (4) \quad f_nx^n=f_{n-1}x^n+f_{n-2}x^n$
עכשיו נסכם את שני צדדי (4) על $latex n$ מ- 2 ל- $latex \infty$:
$latex \displaystyle (5) \quad \sum_{n=2}^\infty f_nx^n=\sum_{n=2}^\infty f_{n-1}x^n+\sum_{n=2}^\infty f_{n-2}x^n$
מתקיים
$latex \displaystyle (6) \quad \sum_{n=2}^\infty f_nx^n=\sum_{n=1}^\infty f_nx^n-f_1x=F(x)-f_1x=F(x)-x$
$latex \displaystyle (7) \quad \sum_{n=2}^\infty f_{n-1}x^n=x\sum_{n=2}^\infty f_{n-1}x^{n-1}=x\sum_{n=1}^\infty f_nx^n=xF(x)$
$latex \displaystyle (8) \quad \sum_{n=2}^\infty f_{n-2}x^n=x^2\sum_{n=2}^\infty f_{n-2}x^{n-2}=x^2\sum_{n=0}^\infty f_nx^n=x^2F(x)$
מ- (5)-(8) נובע כי $latex F(x)-x=xF(x)+x^2F(x)$; או
$latex \displaystyle (9) \quad (1-x-x^2)F(x)=x$
כאן המקום להזכיר כי אנו יודעים ש- $latex F(x) \lt \infty$ עבור $latex 0\le x \lt \frac12$.משום כך כל האלגברה הנ"ל היא "כשרה" עבור $latex 0\le x \lt \frac12$. וכך קיבלנו נוסחה ל-$latex F(x)$:
$latex \displaystyle (10) \quad sum_{n=0}^\infty f_nx^n=F(x)=\frac x{1-x-x^2}, \ 0\le x<\frac12$
אם נדע לפתח את הפונקציה $latex \frac{x}{1-x-x^2}$ לטור חזקות, כלומר נדע את המקדמים, נדע את מספרי פיבונצ'י. מתברר שלא כל כך קשה לפתח את הפונקציה הזאת לטור חזקות. עושים זאת בעזרת שיטה שנקראת שברים חלקיים.
הצעד הראשון בשיטה הזאת הוא לפרק את המכנה לגורמים ליניאריים. את זה אתם בוודאי יודעים לעשות - זה מצריך פתרון של המשוואה הריבועית $latex x^2+x-1=0$. לפי הנוסחה לפתרון משוואה ריבועית, השורשים של $latex x^2+x-1$ הם $latex \frac{-1 \pm\sqrt5}2$; נסמן
$latex \displaystyle r^+=\frac{-1+\sqrt5}2\approx.618,\ \ r^-=\frac{-1-\sqrt5}2$
קל לחשב:
$latex \displaystyle r^-r^+=(\frac{-1-\sqrt5}2)(\frac{-1+\sqrt5}2)=-1$
(הדבר נובע גם מנוסחת ויאטה — מכפלת השורשים היא האיבר החופשי.)
מכאן נובע ש: $latex (x-r^+)(x-r^-)=-r^-r^+(x-r^+)(x-r^-)=-(xr^-+1)(xr^++1)$.
כעת נשתמש בשיטת השברים החלקיים כדי להציג את הפונקציה $latex \frac x{1-x-x^2}$ כטור חזקות עם מקדמים מפורשים. מתקיים
$latex \displaystyle x^2+x-1=(x-r^+)(x-r^-)=-(xr^-+1)(xr^++1)$
לכן מתקיים
$latex \displaystyle (11) \quad \frac x{1-x-x^2}=\frac x{(xr^-+1)(xr^++1)}$
נרשום
$latex \displaystyle (12) \quad \frac x{(xr^-+1)(xr^++1)}=\frac \alpha{xr^-+1}+\frac \beta{xr^++1}$
שיטת השברים החלקיים אומרת שבהכרח קיימים $latex \alpha$ ו-$latex \beta$ שמקיימים את השוויון הזה. ואמנם, אנחנו נמצא אותם. מתקיים
$latex \displaystyle \frac \alpha{xr^-+1}+\frac \beta{xr^++1}=\frac{x(\alpha r^++\beta r^-)+(\alpha+\beta)}{(xr^-+1)(xr^++1)}$
לכן
$latex \displaystyle \frac x{(xr^-+1)(xr^++1)}=\frac{x(\alpha r^++\beta r^-)+(\alpha+\beta)}{(xr^-+1)(xr^++1)}$
על פי השוואת מקדמים, אפשר להסיק כי $latex \alpha r^++\beta r^-=1$ ו- $latex \alpha+\beta=0$. פותרים את שתי המשוואות האלה ומקבלים $latex \alpha=\frac1{r^+-r^-}=\frac1{\sqrt5}$ ו- $latex \beta=\frac1{r^-r^+}=-\frac1{\sqrt5}$. אנו מציבים עבור $latex \alpha$ ו- $latex \beta$ ב- (12) ומשתמשים ב- (11) כדי לקבל
$latex \displaystyle (13) \quad \frac x{1-x-x^2}=\frac1{\sqrt5}\Big(\frac1{1+xr^-}-\frac1{1+xr^+}\Big)$
נתבונן ב- $latex \frac1{1+xr^-} = \frac1{1-(-xr^-)}$. אם נסמן $latex y=-xr^-$, נוכל ליישם את (2) ל- $latex \frac1{1+xr^-}$ אם $latex x$ מקיים $latex |-xr^-|<1$; כלומר, אם
$latex \displaystyle |x| \lt \frac1{|r^-|}=\frac2{1+\sqrt{5}}=\frac{\sqrt{5}-1}2$
באופן דומה, אם נסמן $latex y=-xr^+$, נוכל ליישם את (2) ל- $latex \frac1{1+xr^+}$ אם $latex x$ מקיים $latex |-xr^+| \lt 1$; כלומר, אם
$latex \displaystyle |x| \lt \frac1{|r^+|}=\frac2{-1+\sqrt{5}}=\frac{\sqrt{5}+1}2$
מכיוון ש-$latex \frac{\sqrt{5}+1}2 \gt \frac{\sqrt{5}-1}2$, נוכל ליישם את (2) גם ל- $latex \frac1{1+xr^-}$ וגם ל- $latex \frac1{1+xr^+}$ עבור $latex x$ שמקיים $latex |x| \lt \frac{\sqrt{5}-1}2$. אז מתקיים
$latex \displaystyle (14) \quad \frac1{1+xr^-}=\sum_{n=0}^\infty(-xr^-)^n=\sum_{n=0}^\infty(\frac{1+\sqrt5}2)^nx^n$
ו-
$latex \displaystyle (15) \quad \frac1{1+xr^+}=\sum_{n=0}^\infty(-xr^+)^n=\sum_{n=0}^\infty(\frac{1-\sqrt5}2)^nx^n$
מ- (13)-(15) אנו מגיעים למסקנה כי
$latex \displaystyle (16) \quad \frac x{1-x-x^2}=\sum_{n=0}^\infty\frac1{\sqrt5}\Big((\frac{1+\sqrt5}2)^n-(\frac{1-\sqrt5}2)^n \Big)x^n, \ 0\le x \lt \frac{\sqrt{5}-1}2$
אם נשווה את (10) ו- (16), נוכל להסיק ש:
$latex \displaystyle (17) \quad \sum_{n=0}^\infty f_nx^n=\sum_{n=0}^\infty\frac1{\sqrt5}\Big((\frac{1+\sqrt5}2)^n-(\frac{1-\sqrt5}2)\Big)x^n,\ 0\le x \lt \frac12$
עכשיו אנו מזכירים משפט יסודי מחדו"א.
תהיינה $latex \{a_n\}_{n=0}^\infty$ ו- $latex \{b_n\}_{n=0}^\infty$ סדרות ויהא $latex C \gt 0$. נניח שטור החזקות $latex \sum_{n=0}^\infty a_nx^n$ מתכנס עבור $latex 0\le x \lt C$, ושמתקיים $latex \sum_{n=0}^\infty a_nx^n=\sum_{n=0}^\infty b_nx^n$, עבור $latex 0\le x \lt C$. אזי $latex a_n=b_n$ לכל $latex n$.
מיישמים את המשפט הנ"ל ל- (17), כאשר $latex a_n=f_n$, $latex b_n=\frac1{\sqrt5}\Big((\frac{1+\sqrt5}2)^n-(\frac{1-\sqrt5}2)\Big)$ ו-$latex C=\frac12$; המסקנה היא שהנוסחה המפורשת עבור האיבר ה- $latex n$-י בסדרת פיבונצ'י היא
$latex \displaystyle f_n=\frac1{\sqrt5}\Big((\frac{1+\sqrt5}2)^n-(\frac{1-\sqrt5}2)^n\Big)$
עכשיו שיש בידינו נוסחה מפורשת ל- $latex f_n$, נוכל להראות בקלות שרדיוס ההתכנסות האמיתי של $latex \sum_{n=0}^\infty f_nx^n$ הוא $latex \frac2{1+\sqrt{5}}\approx.618$. אנו משאירים את זה לקורא - הטור $latex \sum_{n=0}^\infty f_nx^n$ הוא הפרש של שני טורים גיאומטריים. רצוי להדגיש כמה חשוב היה הצד הראשון בהוכחתנו - חישוב גס המראה שרדיוס ההתכנסות הוא חיובי אפשר לנו להפעיל את המשפט הנ"ל עם $latex C=\frac12$.
שימו לב כי $latex \frac{1+\sqrt5}2\approx1.618$ ו- $latex \frac{1-\sqrt5}2\approx-.618$.מכיוון ש- $latex \frac{1-\sqrt5}2 \lt 0$, הסימן של $latex (\frac{1-\sqrt5}2)^n$ מתחלף - שלילי עבור $latex n$ אי-זוגי וחיובי עבור $latex n$ זוגי. הרבה יותר חשוב, שימו לב כי לכל $latex n\ge0$ מתקיים
$latex \displaystyle |\frac1{\sqrt{5}}(\frac{1-\sqrt5}2)^n|\le \frac1{\sqrt{5}} \lt \frac12$
לכן, מכיוון ש- $latex f_n$ הוא מספר שלם, נובע כי $latex f_n$ הוא המספר השלם הקרוב ביותר ל- $latex \frac1{\sqrt5}(\frac{1+\sqrt5}2)^n$. למשל, חישוב במחשבון מגלה כי $latex \frac1{\sqrt5}(\frac{1+\sqrt5}2)^{50}\approx12586269024.99998$; לכן $latex f_{50}=12,586,269,025$.
אכן הפונקציה $latex F(x)=\frac x{1-x-x^2}$ "יצרה" לנו את מספרי פיבונצ'י!
מה זו לוגיקה מתמטית
אנה ליזהטוב
מהי המתמטיקה?
"המדע של הצורה והמספר", אומרת אחת ההגדרות המפורסמות ביותר. כלומר - גיאומטריה ומספרים. האמנם? לא אנסה במאמר הזה להגדיר מהי המתמטיקה (כדאי שתנסו בעצמכם!) אבל אראה לכם בו שהטענה הזאת אינה נכונה. המאמר הזה הוא ראשון בסדרת מאמרים על תחום מתמטי שמפריך בקיומו את ההגדרה הזאת: הוא אינו עוסק לא בצורות ולא במספרים. זוהי הלוגיקה המתמטית - אחד החידתיים ביותר בין תחומי המתמטיקה. תחום שלא ברור איך יכולים בכלל להיאמר בו דברי טעם. אבל נאמרים, ועוד איך.
הלוגיקה המתמטית היא המתמטיקה של המתמטיקה. כפי שאיש משוואות דיפרנציאליות מסתכל בזרימה בצינורות, מוצא את המשוואות הדיפרנציאליות שעל פיהן הנוזלים בצינור מתנהגים ואחר כך חוקר את המשוואות האלה, כך הלוגיקאי מסתכל במתמטיקאים, כיצד הם יושבים במשרדיהם, מחדדים את עפרונותיהם, בוהים בלוח שלפניהם, מתגרדים בראשם - ועושים מתמטיקה. אכן, כפי שאתם יכולים לנחש, על החלק של הגירוד בפדחת הלוגיקאי מדלג. במקום זאת הוא מסתכל במה שהמתמטיקאי כותב במחברתו.
במשך כאלפיים שנים אכן הייתה הלוגיקה המתמטית מקצוע דל ביותר. היחיד שהתייחס אליה ממש היה אריסטו, שקבע כמה כללי היסק. כלומר, כללים שבעזרתם אפשר להסיק ממשפטים מסוימים משפטים אחרים. המפורסם ביניהם היה "ניתוק הרישא", או ביוונית "מודוס פוננס" ("MODUS PONENS"). הכלל הזה אומר שאם הצלחתם להוכיח ש"אם היום יום שלישי אז חייב לרדת גשם", ובמקביל הצלחתם להוכיח גם ש"היום יום שלישי", אתם יכולים להסיק ש"היום יורד גשם". את המשפט "אם $latex \ldots$ אז" מסמנים בלוגיקה על ידי חץ:
$latex \alpha \to \beta$ פירושו "אם $latex \alpha$ אז $latex \beta$". מיהם $latex \alpha$ ו-$latex \beta$? ובכן, כל שתי טענות. אפשר להציב במקומם כל טענות שתרצו. ניתוק הרישא אומר אם כן: אם הצלחתם להוכיח ש-$latex \alpha \to \beta$ וגם $latex \alpha$, הרי הוכחתם בזאת $latex \beta$.
חוכמה גדולה? לא נראה כך, לפחות ממבט ראשון. אבל כאן טמונים כבר הזרעים של מקצוע הלוגיקה. הרעיון הבסיסי, של להסתכל על המשפטים שהמתמטיקאים אומרים כעל מחרוזות של תווים (אותיות) ולשחק עם המחרוזות האלה על פי כללים קבועים וידועים, נמצא כבר כאן. הכללים האלה הם פורמליים, כלומר נוגעים למבנה המשפט (מה שנקרא בלוגיקה "תחביר") ולא למשמעות המשפט.
ובכל זאת, איך ממשיכים? "אי אפשר להמשיך", אמר הפילוסוף עמנואל קאנט בסביבות שנת 1800. "על מה שאמר אריסטו על הלוגיקה אין להוסיף אפילו מילה אחת". קאנט הקדיש את כל הקריירה הפילוסופית שלו לעשות דבר אחד - להוכיח שמה שיש הוא בדיוק מה שצריך להיות. חוקי הגיאומטריה, כך אמר, אינם יכולים להיות שונים מאלה של הגיאומטריה האוקלידית: כחמישים שנים אחר כך יבהירו גאוס ובויוי שהגיאומטריה יכולה להיות שונה מאוד, וכעבור חמישים שנים נוספות יראה איינשטיין שהעולם מציית דווקא לחוקיה של גיאומטריה לא אוקלידית. קאנט ניסה להראות שחייבת להיות סיבתיות בעולם (אחרת לא נוכל בכלל לחשוב - והרי אנחנו חושבים), ושאת חוקי המוסר אפשר להסיק מכלל אוניברסלי (הוא התעלם מכך שחוקי המוסר של חברות שונות הם שונים מאוד). כך הוא גם טען שהלוגיקה של אריסטו היא בדיוק מה שצריך להיות - המילה האחרונה. אבל לא כדאי לקחת פילוסופים יותר מדי ברצינות כשהם מדברים על מתמטיקה. לא עברו חמישים שנים מאז שאמר קאנט את מה שאמר על הלוגיקה, וגלגליה של מהפכה לוגית החלו לנוע.
הצעד הראשון נעשה בידי לוגיקאי אנגלי בשם ג'ורג' בול. לבול לא היו חיים קלים. כנער נאלץ לפרנס את משפחתו בשיעורים פרטיים, וכך לא למד בצורה מסודרת בעצמו: הוא היה אוטודידקט. לאחר קריירה לא ארוכה מת בגיל כחמישים מדלקת ריאות, שהוחמרה בטיפולים של אמבטיות קרות בהמלצת אשתו שהאמינה ש"התרופה צריכה להיות דומה לגורם למחלה".

ג׳ורג׳ בול, 1815 - 1864
על כל זאת פיצתה אותו אלת המתמטיקה במתנה גדולה: ייסוד תחום חדש. בול הבין שאפשר לחקור את הדרך בה מצרפים משפטים מתמטיים זה לזה, על ידי פעולות פשוטות. הפעולות הפשוטות ביותר הן "או" ו-"ו", שמסומנות ב-$latex \vee$ ו-$latex \wedge$, בהתאמה. כך, $latex \alpha \vee \beta$ משמעה $latex \alpha$ או $latex \beta$, שהיא טענה נכונה (כך מגדירים) בתנאי שלפחות אחת משתי הטענות נכונות. הטענה $latex \alpha \wedge \beta$, לעומת זאת, נכונה (ושוב זה עניין של הגדרה) אם שתי הטענות נכונות. הסימן "$latex \to$" מסמן כאמור, גרירה, והטענה $latex \alpha \to \beta$ נכונה (כך מגדירים) אם $latex \beta$ נכונה, או $latex \alpha$ לא נכונה. במילים אחרות, הטענה $latex \alpha \to \beta$ אינה נכונה רק במקרה אחד: כאשר $latex \alpha$ נכונה ו-$latex \beta$ אינה נכונה. לשלילה מותאם הסימן $latex \sim$. $latex \sim \alpha$ משמעו "לא נכון ש- $latex \alpha$".
עתה אפשר לומר דברים מעניינים על הנוסחאות. למשל, שקילות בין נוסחאות. מה פירוש "שקילות"? שתי נוסחאות שמכילות משתנים לוגיים נקראות שקולות אם הן מקבלות אותו ערך אמת לכל הצבה של ערכים למשתנים. הנה שתי דוגמאות:
2. $latex \sim (p \vee q)$ שקולה ל-$latex \sim p \wedge \sim q$. יש ארבע אפשרויות לבחירת ערכי אמת לשני המשתנים. בדקו שבכל אחת מהן שתי הנוסחאות מקבלות אותו ערך אמת. או, פשוט חישבו על המשמעות של "לא נכון ש-א' או ב' " ותיווכחו שפירושו שגם א' לא נכון, וגם ב' לא נכון. החוק הזה נקרא "חוק דה מורגן".
יש עוד חוק של דה מורגן - $latex \sim (p \wedge q)$ שקולה ל - למה? השלימו את החסר, ונסו גם להסיק את החוק השני מן הראשון, בעזרת החוק על $latex \sim \sim \alpha$.
זו הייתה התקדמות גדולה - אמנם זה לא מורכב במיוחד, אבל יש כאן מהפכה מושגית. הסתכלות חדשה על המשחק המתמטי. המתמטיקאים, כך אמר בול, הם שחקנים שלוח המשחק שלהם הוא שרשראות של נוסחאות. והנכונות של נוסחה מורכבת מוגדרת על פי הנכונות של המרכיבים האטומיים שלה (אלה שאינם ניתנים לחלוקה) שלה - בדוגמאות שלעיל המרכיבים האטומיים היו $latex p$ ו-$latex q$.
ועדיין, רוב המתמטיקאים לא התרגשו. הם חיכו שדבר מה עמוק ייאמר על התורה החדשה. היו נחוצות עוד התפתחויות כדי שהתחום יגיע לבשלות. הראשונה בהן נעשתה ברבע האחרון של המאה התשע עשרה, בידי לוגיקאי בשם פרגה ($latex Gottlob~~Frege$). הוא עשה שני דברים מהותיים. האחד - הוא הוסיף ממד לנוסחאות, בדמות סימן חדש, שהוחלף מאז ב: $latex \forall$. הסימן הזה אומר "לכל", והוא דורש משתנה: $latex \forall x$ משמעו לכל ערך של המשתנה $latex x$. למשל, בתורת המספרים אפשר לכתוב את הנוסחה $latex \forall x (x \ge 0)$ - שבאינטרפרטציה הרגילה של הסימן $latex \ge$ ושל הסימן $latex 0$ זוהי טענה נכונה (באינטרפרטציה הרגילה הסימן $latex 0$ מותאם למספר $latex 0$).
מאוחר יותר הוסיף מתמטיקאי בשם פאנו סימן נוסף - $latex \exists$, שמשמעו "קיים". פרגה הסתדר בלעדיו - כיצד? הוא שם לב לכך שאת הטענה "קיים משהו" אפשר לבטא בעזרת "לכל". "קיים בארץ אדם שאוהב לשים חרדל על העוגה שלו" שקול ל-"לא כל אדם בארץ לא אוהב לשים חרדל על העוגה שלו". ובאופן כללי -
הנוסחה $latex \exists x (P(x))$ שקולה לנוסחה $latex \sim(\forall x \sim P(x))$. כאן $latex P(x)$ היא תכונה כלשהי של המשתנה $latex x$ - למשל לאהוב עוגה עם חרדל.
אבל זה היה רק צעד ראשון של פרגה. היה לו צעד חשוב הרבה יותר - הוא הגדיר בצורה מדויקת מהי "הוכחה מתמטית". וזה היה כבר באמת הישג גדול. אספר עליו במאמר הבא בסדרה.
ראיון עם דורון ציילברגר מאוניברסיטת רטגרס, ניו ג'רזי
רון אהרוני
פרופ' ציילברגר הוא מתמטיקאי ידוע ומוכר בשל הישגיו בתחום המנייה הקומבינטורית. אבל לא פחות מכך הוא מפורסם בשל פריצת הדרך שלו בכתיבת תוכניות מחשב שמגלות בעצמן משפטים מתמטיים, במיוחד זהויות קומבינטוריות. את דעתו, שבסופו של דבר המחשבים יוכלו למלא לא רק את מקומם של מחשבי חשבונות אלא גם של מתמטיקאים, הוא מפיץ בדרכים שונות. בראיון הזה ניסינו להתחקות אחרי התפתחותו כמתמטיקאי ולשמוע מעט מדעותיו.
מתי נוכחת לדעת שאתה רוצה להיות מתמטיקאי?
נולדתי בחיפה ב-1950, אך מייד עם היוולדי עברה המשפחה לקריית מוצקין. שם גרתי, עם הורי ועם אחי הצעיר, עד גיל 14, ואז עברנו לחולון. עד לכיתה ו' לא הייתי טוב במיוחד במתמטיקה, וגם לא אהבתי אותה במיוחד. הדברים השתנו בכיתה ז', שבה פגשתי במורה כריזמטית ומעוררת השראה בשם דבורה שגב, שעשתה את המתמטיקה לכיף.
כל קיץ נסעתי עם אחי הקטן (לבדנו!) לירושלים לבקר את "דודה גיטי" ובעלה, "דוד הנס". דודי הנס, שהיה עורך דין, היה גם אסטרונום חובב, ובזכותו התחלתי לקרוא את עיתון האגודה הישראלית לחובבי אסטרונומיה. הייתי משוכנע שכאשר אגדל אהיה אסטרונום.
הדודים מירושלים היו "יקים", וחתמו על עיתון גרמני בשם "שטרן". אני הייתי מנסה את החידות המתמטיות שם, של השלמת ספרות בתרגילי חשבון. נעשיתי טוב מאוד בזה.
בכיתה ח' היו שתי נקודות מפנה. האחת – קראתי את הספר "מתמטיקה למיליון" של הוגבן, מכריכה לכריכה, ולימדתי את עצמי את כל המתמטיקה שהייתה שם, כולל החשבון הדיפרנציאלי, גיאומטריית המישור והמרחב, וסטטיסטיקה.
עוד יותר חשוב מכך, בנו של הנס היה חתום על הסב-סבא של "נטגר", "גיליונות מתמטיקה", בעריכתו של פרופ' גיליס המנוח. היו שם הרבה מאמרים מרתקים, בחלקם הגדול כתובים בידי גיליס עצמו, ובמיוחד היו שם בעיות, שאותן ניסיתי לפתור, די בהצלחה. זו הייתה הנקודה שבה באמת התאהבתי במתמטיקה.
בתיכון אהבתי מתמטיקה כל כך שהתעלמתי מכל שאר המקצועות. התמכרתי ל"גיליונות מתמטיקה", וקראתי מאמרים מתקדמים במתמטיקה. כתוצאה מהזנחת המקצועות האחרים נזרקתי מבית הספר בכיתה י'. למגינת ליבם של הורי החלטתי לפתוח בקריירה של נער שליחויות. עשיתי זאת כשנה.
אחרי השנה הזאת אבי, שהיה מורה לאנגלית, עשה שנת שבתון באוניברסיטת קיימברידג'. שם למדתי לבגרות אנגלית – למזלי באנגליה מותר היה להתמחות, ואני עשיתי בחינות רק במתמטיקה עיונית, מתמטיקה שימושית (בשתיהן הצלחתי) ובפיזיקה (שם עברתי בקושי).
כשחזרתי לארץ הייתה לי חצי שנת חופש לפני הגיוס, ואני ביקשתי מפרופ' גיליס שיקבלני לעבודת קיץ. למזלי הוא קיבל אותי, ואני הייתי אמור לעזור לתלמיד דוקטורט שלו בתכנות. לשם כך (למזלי, כפי שיתברר) למדתי את שפת התכנות פורטרן, אלא שמכיוון שעשיתי גם דברים מעבר למה שתלמיד הדוקטורט דרש הוא פיטר אותי. עברתי אז לעבוד עם נירה דין, לימים פרופסורית באוניברסיטת תל אביב, ויחד איתה ועם תלמיד מחקר אחר כתבנו מאמר שעבורי היה הראשון בקריירה.
בפברואר 1969 התגייסתי לחיל התותחנים. שם השתמשתי בידע המתמטי שלי לחישוב מסלולי פגזים – בכך נכנסתי קצת לצרות, משום שחברי דבקו בשיטות גרפיות. בעת שירותי בסיני נרשמתי ללימודים בהתכתבות באוניברסיטת לונדון, וסיימתי את התואר שם, בהצטיינות, תוך כדי שירותי.
החלטתי לחזור למכון וייצמן, לעשות דוקטורט. בחרתי כמנחה בהרי דים, חבר סגל צעיר בפקולטה. סיימתי את הדוקטורט ארבע שנים אחר כך, בגיל 26, שהוא גיל צעיר לישראלי ששירת בצבא.

מהם הסיפוקים בחייו של מתמטיקאי? האם יש גם נקודות צל?
חברי סגל של אוניברסיטאות הם בעלי מזל: הם מקבלים משכורת לעשות מה שהם אוהבים. למי שאינו אוהב ללמד יש קצת בעיה, אבל אני, ואינני היחיד בכך, אוהב ללמד. נקודה בעייתית אחרת היא התחרות האקדמית, והלחץ על אקדמאים בשלבים המוקדמים, לפני שהם מקבלים קביעות. אבל מן הרגע שאתה מקבל קביעות, אתה חופשי. לפעמים יש גם בעיה של שיפוט מאמרים – לא אחת קורה שהשופט של מאמר בכלל לא מבין במה מדובר.
אבל במקרה שלי, לפחות, הבנתי בשלב כלשהו שאינני חייב להשתתף במשחק. כיום אפשר לפרסם את המאמרים באינטרנט, במיוחד ב"ארכיב" (arXiv), שבו אפשר לשים את המאמרים שלך והם נקראים על ידי הקהילה.
אילו מתמטיקאים השפיעו עליך במיוחד?
רבים! כבר הזכרתי את יוסף גיליס. גם הרי דים, המנחה שלי, שהיה איש אנליזה יוצא דופן, השפיע עלי, אף על פי שערקתי מן האנליזה למתמטיקה דיסקרטית (שם נרדף ל"קומבינטוריקה"). מתמטיקאי אחר שהשפיע עלי היה יקר קנאי, שלימד אותי את תאוריית ה-D-מודולים של ברנשטיין (עובד כיום באוניברסיטת תל אביב), שהייתה בסופו של דבר אבן הפינה של מה שקרוי כיום "תורת ההוכחה האלגוריתמית של וילף-ציילברגר". וילף היה המורה שלי בקומבינטוריקה, ולמדתי גם מן המתמטיקאים הצרפתיים פואטה וויינו (Foata, Vienot).
מה המקום של היופי בעבודתך?
יופי הוא רק בעומקים הרדודים. המתמטיקה היפה ביותר היא כזו בגלל פשטותה. כשם שאדם יפה הוא הנאה לעין, גם מתמטיקה יפה היא הנאה לשכל, אבל אסור לתת לה משקל מעבר למה שיש לה. מטרתה של המתמטיקה היא לגלות ידע שהוא עמוק, משמעותי ושימושי. המתמטיקה שמייצר המחשב, כזו שאני והמחשבים שלי עושים, היא לעתים קרובות מכוערת לשכל האנושי, אבל בעיני זה דווקא הופך אותה ליפה עוד יותר – יופי שמעבר ליופי הרגיל.
דף הויקיפדיה שלך אומר שאתה "אולטרא-פיניטיסט" – מה זה אומר?
כשם שאתה (רון אהרוני) טוען שהבעיות הפילוסופיות כולן מקורן בטעות של בניית מושגים על דרך ההתייחסות העצמית, כך גם לי יש מריבה עם מושג האינסוף. מושג האינסוף הביא תועלת, אבל עוד יותר מכך גרם לנזק. אני סבור שאם מושג האינסוף יוחלף במושג "אינסוף" (עם מרכאות כפולות), שפירושו שזהו מושג שנדון בתוך תורות שמדברות רק על אובייקטים סופיים, אפשר לשכתב את כל המתמטיקה במונחים סופיים, והשאר אינו ראוי שייעשה!
לבסוף, אנא ספר לנו על דעותיך השנויות במחלוקת על עתיד המתמטיקה, ואיך היא צריכה להיעשות.
המתמטיקה המוכרת לנו היא כזו משום שהיא נעשית על ידי בני אנוש, עם נייר ועיפרון. משהו נוסף שמעכב את התפתחותה הוא הדעה הדתית-פנאטית, שכל ידע מתמטי צריך להיות מוכח בצורה מדויקת. כל זה ייעלם בקרוב. השימוש במחשבים ירחיב את האופקים המתמטיים שלנו כמעט עד אינסוף. כשזה יקרה, נזנח את רעיון ה"ביטחון המלא", ונלמד לחיות עם עובדות שהן רק 99.99999999999999999999999999% בטוחות.
האם יש לך עצה למתמטיקאי מתחיל, או גם לא כל כך מתחיל?
למד או למדי איך לתכנת מחשב, היטב! הטוב ביותר הוא להכיר תוכנות על, כמו Maple , או Mathematica, או התוכנה החדשה והחינמית Sage. כשאתה מנסה לפתור בעיה, היפטר מן הגישה הילדותית שעליך לפתור אותה בעצמך. מוטב שתחשוב איך תלמד מחשב לפתור אותה. בסופו של דבר, התוכנית תצליח לפתור גם בעיות קשות הרבה יותר, ששום בן אנוש לא יצליח לפתור.
כמובן, בזמנך הפנוי אתה יכול להשתעשע גם בפתרון הבעיה בדרך הישנה, בעצמך. אבל זה צריך להיות שעשוע, כמו סודוקו. ועל זה אינך אמור לקבל משכורת.
חידות
דניאל לובזנס
לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 24.11.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1–איך לחלק את המחרוזת?

שני גנבים רוצים להתחלק בשללם, מחרוזת שבה מושחלים בזה אחר זה $latex 2n$ ספירים ו $latex 2m$ אזמרגדים (באיור $latex n=1, m=3$). אבני החן מסודרות באפן שרירותי על המחרוזת, יש להראות כי לכל סידור נתן לחתוך את המחרוזת ל3 חלקים כך שגנב אחד יקבל את החלק המרכזי עם $latex n$ ספירים ו $latex m$ אזמרגדים, ובחלקו של השני יהיו 2 החלקים הקיצוניים, גם הם עם $latex n$ ספירים ו $latex m$ אזמרגדים.
זה מקרה פרטי של הבעיה המוצגת בגיליון הקודם של "נטגר" במאמרו של רון אהרוני על טופולוגיה, הבעיה הכללית דורשת שימוש במשפט בורסוק-אולם. לעומת זאת החידה שבה יש רק שני סוגי חרוזים, המופיעה במדור זה ניתנת לפתרון פשוט, שגם נותן לגנבים אלגוריתם למציאת נקודות החיתוך.
חידה 2–איך למצוא את הדרך הנכונה?
חידה זו הוצעה בשעתו ע"י מרטין גרדנר. לאלו שאינם מכירים, מצפה אתגר.
תייר מגיע לאי שבו יש שני שבטים: האחד של דוברי אמת – על כל שאלה עונים את התשובה הנכונה. ואחד של דוברי שקר – על כל שאלה נותנים תשובה שקרית, במיוחד אם התשובה הנכונה היא "כן" הם אומרים "לא", ולהפך אם התשובה הנכונה היא "לא" הם אומרים "כן". אנשי אחד מהשבטים חובשים כובעים ואנשי השבט השני מסתובבים גלויי ראש.
התייר מגיע לצומת ממנו מתפצלות שתי דרכים האחת ימינה והשנייה שמאלה, ידוע לו שרק אחת הדרכים מובילה לארמון המלך. בצומת נצבים שני תושבי האי, האחד עם כובע על ראשו והשני גלוי ראש.
מותר לתייר לשאול שאלה אחת בלבד, שהתשובה עליה היא כן או לא, השאלה יכולה להיות מופנית לאחד מתושבי האי בלבד. מה ישאל התייר כדי למצוא את דרכו לארמון?
חידה 3– סידור אבני דומינו?

משחק דומינו רגיל מורכב מ 28 אבני משחק על כל אחת מהן זוג מספרים שכל אחד מהם בין 0 ל 6 . מופיעים כל זוגות המספרים האפשריים וכל אבני הדומינו שונות זו מזו . בוודאי ידוע לכם שאפשר לסדר את כל אבני הדומינו בשרשרת אחת שבה המספרים הנושקים זה לזה זהים. הציור מראה קטע של שרשרת כזו (עם האבנים: $latex \dots$ 5:6,6:4,4:3,3:5)
האם במשחק דומינו מורחב שבו המספרים על האבנים הם בין 0 ל 9 (סה"כ 55 אבני משחק) גם כן ניתן לסדר את האבנים בשרשרת אחת שבה המספרים הנושקים זה לזה זהים?
רמזים לחידות מגיליון אוקטובר 2015
חידה 1–שמיכת טלאים
נסו לפתור חידה פשוטה יותר שמיכה מרובעת של 25 ריבועים לחלק ל 2 שמיכות 3X3 ו 4X4, בחלוקה של השמיכה הגדולה ל 4 חלקים – הכלילו את התוצאה.
חידה 2–איזו ספרה חסרה?
חשבו את המספר מודולו 9.
חידה 3– איזה מספרים ניתן לרשום כסכום של רצף של מספרים טבעיים?
הראו כי אי אפשר לרשום מספרים שהם חזקות של 2 כסכום של רצף.
פתרון החידות גיליון ספטמבר 2015
חידה 1 –כמה פירמידות?
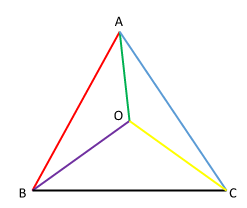
כמובן שכל התמורות של 6 המקצועות, $latex 6!$ , ייצרו הרבה מאד עותקים של אותה פירמידה כשהיא מסובבת. אחת הדרכים לספור נכון את הפירמידות השונות זה להסתכל על צבעי המקצועות המנוגדים (למשל $latex OC$ ו $latex AB$ ) ברור שכל צביעה שבה למקצוע הצהוב יהיה קדקוד משותף עם המקצוע האדום אי אפשר יהיה להתאים ע"י סבוב לפירמידה המצוירת למעלה.
בשלב ראשון נבדוק כמה זוגות שונים מהצורה $latex \left\{a,b\right\},\left\{c,d\right\},\left\{e,f\right\}$ נתן ליצר מ 6 הצבעים $latex (a,b,c,d,e,f)$. קל לראות כי מספר זה שווה ל: $latex \frac{C_2^6 \cdot C_2^4 \cdot C_2^2}{3!} = \frac{\frac{6 \cdot 5}{2} \cdot \frac{4 \cdot 3}{2} \cdot 1}{6} = 15$ המכנה נובע מכך שסדר הזוגות לא משנה.
כל שלשה של זוגות צבעים (של מקצועות מנוגדים) יכולה לכאורה לצבוע את הפירמידה ב 8 דרכים, אך בדיקה פשוטה מראה כי מדובר רק בשתי אפשרויות. האיור הבא מתאר את 8 האפשרויות לשלשה (צהוב-סגול, שחור-כחול, אדום-ירוק)
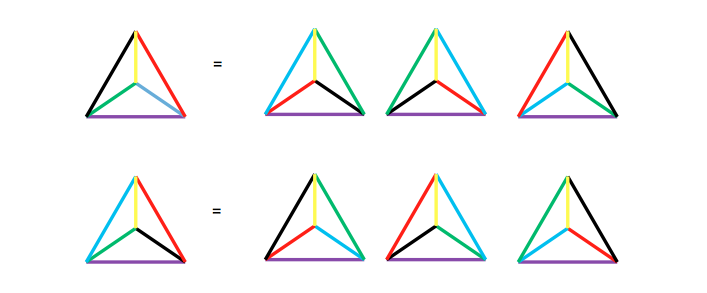
זה נותן לנו 30 אפשריות. מאידך השרטוט בראש החידה מייצג למעשה שני שיקופים של פירמידה, אם נחשוב שהמשולש $latex ABC$ נמצא במישור, הנקודה $latex O$ יכולה להימצא מעליו או מתחתיו וליצור בצורה כזו שתי פירמידות שונות (שאי אפשר לעבור מאחת לשנייה ע"י סבוב כלשהוא). כלומר סה"כ יש 60 אפשרויות.
לגבי בניית פירמידה מ6 מקצועות באורכים שונים $latex a_1 \lt a_2 \lt a_3 \lt a_4 \lt a_5 \lt a_6$. לכאורה צריך לבדוק את אי שוויון המשולש לגבי כל 3 אורכים. כלומר לכל $latex i,j,k$ צריך להתקיים $latex a_i + a_j \gt a_k$. אבל מאחר והקטעים מסודרים לפי אורכם מספיק לבדוק אי שוויון אחד בלבד: $latex a_1 + a_2 \gt a_6$ !
חידה 2–האם ניתן לכסות לוח שחמט פגום ב 31 אבני דומינו?
אבן דומינו תמיד מכסה משבצת אחת שחורה ומשבצת אחת לבנה, לכן 31 אבני דומינו יכסו 31 משבצות שחורות ו 31 משבצות לבנות. בלוח השח הפגום יש 30 משבצות לבנות ו 32 שחורות, לכן זה בלתי אפשרי.
חידה 3 – בפרוס שנת תשע"ו
קודם כל יש לתת את הדעת שההפרש בין השנה בלוח העברי לשנה בלוח הגרגוריאני יכול להיות 3760 (בין 1 ינואר ל כ"ט באלול) או 3761 (בין א' תשרי ל 31 דצמבר).
אם נסמן ב $latex a^2$ את השנה לפי הלוח העברי, וב $latex b^2$ את השנה לפי הלוח הגרגוריאני.
נשתמש בשוויון $latex a^2-b^2 = (a+b) \cdot (a-b)$ ונקבל שהמכפלה בצד ימין של המשוואה היא הגורמים של ההפרש בין ערכי השנים בלוחות השונים. מפרוק לגורמים נקבל:
$latex 3761 = 1 \cdot 3761$
$latex 3760 = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 5 \cdot 47$
ומכאן קל למצוא שאם נדרוש שההפרש בין השנים יהיה 3761 יהיה פתרון אחד בלבד (שנצטרך לחכות לו מיליוני שנים): השנה לפי הלוח העברי תהיה 3,538,161 –ואז השנה לפי הלוח הגרגוריאני תהיה 3,534,400.
במקרה השני, יש לתת את הדעת שלפתרונות שלמים שני הגורמים חייבים להיות זוגיים, קיימים 6 פתרונות אפשריים.
| מחלקים | שנה עברית | שנה גרגוריאנית | |
|---|---|---|---|
| 40 | 94 | 4489 | 729 |
| 20 | 188 | 10816 | 7056 |
| 10 | 376 | 37249 | 33489 |
| 8 | 470 | 57121 | 53361 |
| 4 | 940 | 222784 | 219024 |
| 2 | 1880 | 885481 | 881721 |
המצב שבו השנים לפי שני הלוחות היו רבועים שלמים קרה לפני למעלה מאלף שנה בשנת ד'תפ"ט שהיא שנת 729.
ואילו לאירוע הקרוב ביותר בעתיד נצטרך להמתין יותר מחמשת אלפים שנים לשנת י'תתט"ז שהיא שנת 7056.
שמות הפותרים נכונה את החידות מגיליון אוקטובר 2015
אלעד צליק – כל החידות!
עומר שמחי, מסיים י"ב, קריית טבעון - חידות מספר 2 ו-3.