נטגר גליון 21
דבר העורך
רון אהרוני
בגיליון זה יש שני מאמרים. האחד, של דויד בלנק מאוניברסיטת חיפה, על איך מחשבים שורש ריבועי. פעם היו מלמדים זאת בבית ספר תיכון - האם אתם מאמינים? השני הוא תרומה של אנה ליזהטוב (כבר אמרנו: אם היא לא הייתה קיימת היה צריך להמציא אותה), על הלוגיקה המתמטית, מן המוזרים בתחומי המתמטיקה. זהו תחום שנדמה שיש בו ניחוח פילוסופי אבל מי שמבין אותו באמת יודע שבדיוק ההפך, הוא מראה שהחשיבה האנושית היא חלק מן העולם הפיזיקלי.
ועכשיו אני רוצה לשתף אתכם במחשבותי. אנחנו רוצים לעשות פסק זמן, כדי לחשוב לאן הוליך את העיתון. חברי המערכת מרגישים לפעמים כקול קורא במדבר. לפי כמות התגובות שמגיעות (כלומר, לא מגיעות), ולפי כמות החידות שנפתרות (כלומר, לא נפתרות, לפחות לא שולחים לנו הרבה פתרונות) נראה שאין עניין רב. האם זוהי תוצאה של שינוי תרבותי כללי? או שמא אופי העיתון אינו מושך קוראים? האם תוכלו, הקוראים, לשלוח לנו את דעותיכם? לאן יש לקחת את העיתון? האם התדירות גבוהה מדי? האם נחוצים מאמרים יותר פופולריים, או להפך - יותר ספציפיים?
בכל מקרה, זמנית אנחנו מפסיקים את הוצאת העיתון, עד שנגיע להחלטה בכיוון כלשהו. אנחנו נעדכן את הגיליון הזה בתגובותיכם. אנא עקבו לראות אם תגובותיכם התפרסמו.
ובינתיים - תודה לכל העושים במלאכה. אורי פרץ ומיכאל ליטבק, שהיו ממונים על הצדדים המחשוביים של הפרויקט. לדני לובזנס שערך את מדור החידות. יוסי כהן, שהיה האחראי והדוחף, אליהו לוי ואנה ליזהטוב שהתמידו כתורמי מאמרים, ולשאר המתמטיקאים שתרמו מזמנם ומן הידע שלהם.
חישוב 2√
דוד בלנק
כולנו מכירים את משפט פיתאגוראס, האומר שריבוע היתר במשולש ישר זווית שווה לסכום ריבועי הצלעות האחרות. המשפט הזה היה ידוע (כעובדה אמפירית לפחות) מאות שנים לפני פיתאגוראס, אך הוא היה הראשון שגילה את העובדה המפתיעה שבכל יחידות אורך שנקבע, אורך הצלע $latex A$ של ריבוע כלשהו ואורך האלכסון שלו $latex B$ אינם בני השוואה - כלומר, אין מספרים שלמים חיוביים $latex m$ ו-$latex n$ כך ש-$latex n\cdot A=m\cdot B$.
אם נקבע את יחידת האורך שלנו להיות יחידה אחת, ממשפט פיתאגוראס נמצא שריבוע אורך האלכסון בריבוע זה שווה ל-$latex 2$, ומכאן נקבל את הניסוח המודרני לתגלית של פיתאגוראס:
משפט: אין $latex p$ ו-$latex q$ שלמים חיוביים כך ש-$latex \sqrt{2}=p/q$ - כלומר, $latex \sqrt{2}$ אינו מספר רציונאלי.
הוכחה: נניח בדרך השלילה שיש מספרים שלמים $latex p,q$ כאלה, ולכן מתקיים:
$latex \displaystyle (1) \quad ~2q^{2}~=~p^{2}$
אם יש ל-$latex p$ ו-$latex q$ גורם משותף $latex 1 \lt d$, אפשר לצמצמו, ולכן מותר להניח ש-$latex p$ ו-$latex q$ זרים. אך מ-(1) אנו רואים ש-$latex p^{2}$ זוגי, ולכן $latex p$ זוגי (מדוע?). נאמר ש-$latex p=2k$ עבור $latex k$ טבעי: אז
$latex ,~2q^{2}~=~p^{2}~=~(2k)^{2}~=~4k^{2}$
כלומר $latex q^{2}=2k^{2}$, ולכן $latex q$ עצמו זוגי - בסתירה לכך ש-$latex p$ ו-$latex q$ זרים. ∎
למרות שאי-אפשר לבטא את $latex \sqrt{2}$ במדוייק באמצעות מספרים רציונאליים, אפשר לקרב אותו - או כל שורש ריבועי אחר - על-ידי מספרים רציונאליים בכל מידת דיוק שנרצה, בדרך שהייתה ידועה כבר לבבלים לפני כמעט 4000 שנה:
השיטה: יהי $latex x$ מספר רציונאלי חיובי כלשהו, ונניח למען הפשטות ש-$latex 1 \lt x$. אנו נבנה שתי סדרות $latex (a_{n})_{n=0}^{\infty}$ ו-$latex (b_{n})_{n=0}^{\infty}$ של קירובים רציונאליים חיוביים ל-$latex \sqrt{x}$, באופן שיתקיים:
(א) $latex a_{n}^{2} \lt x \lt b_{n}^{2}$ (כלומר, $latex a_{n} \lt \sqrt{x} \lt b_{n}$) לכל $latex n$ טבעי.
(ב) $latex a_{n} \lt a_{n+1}$ ו-$latex b_{n} \gt b_{n+1}$ לכל $latex n$ טבעי (כלומר, כל סדרה מונוטונית).
(ג) $latex b_{n}-\sqrt{x} \lt \epsilon$, אז $latex \sqrt{x}-a_{n} \lt \epsilon$ ו-$latex b_{n+1}-\sqrt{x} \lt \epsilon/2$.
שימו לב: שתי הדרישות הראשונות ביחד אומרות שהסדרה $latex a_{1},a_{2},a_{3},\dotsc$ מקרבת את $latex \sqrt{x}$ מלמטה, ואילו הסדרה $latex b_{1},b_{2},b_{3},\dotsc$ מקרבת את $latex \sqrt{x}$ מלמעלה. יתר על כן, שתי הסדרות האלה מונוטוניות - כלומר, בכל פעם הזוג $latex (a_{n+1},b_{n+1})$ הוא קירוב טוב יותר ל-$latex \sqrt{x}$ מאשר הזוג $latex (a_{n},b_{n})$.
אולם אפשר למצוא שתי סדרות כאלה בלי להתאמץ הרבה: למשל, יכולנו לבחור בתור הקירובים ל-$latex \sqrt{2}$ מלמטה את $latex 1, \ 1.1,\ 1.11,\ 1.111$, וכן הלאה, ובתור הקירובים ל-$latex \sqrt{2}$ מלמעלה את $latex 2, \ 1.9,\ 1.89,\ 1.889$, וכן הלאה,
מה שחסר בבחירות אלה הוא מה שנותנת דרישה (ג): שהסדרות אכן מתקרבות כרצוננו ל-$latex \sqrt{x}$. זאת נקודה קצת עדינה, משום שאין לנו דרך לחשב את $latex \sqrt{x}$ עצמו ולהשוות אליו את הקירובים שלנו. אנו משתמשים איפוא במה שהיוונים כינו שיטת המיצוי: אנו מייצרים שתי סדרות של קירובים, ודואגים לכך שסדרה אחת תמיד קטנה מ-$latex \sqrt{x}$, והשניה תמיד גדולה מ-$latex \sqrt{x}$. זה מה שאומרת דרישה (א): שימו לב שהיא מנוסחת באמצעות $latex x$ (שהוא מספר רציונאלי, לפי ההנחה), ואינה מזכירה את $latex \sqrt{x}$. בעצם אנו מנצלים כאן רק את העובדה שפונקציית ההעלאה הריבוע היא מונוטונית עבור מספרים אי-שליליים.
אם בנוסף לכך נבטיח שהקירובים מלמטה ומלמעלה מתקרבים זה לזה כרצוננו - כפי שקורה בדרישה (ג) - הרי שמרחק כל אחד מהם מהמספר המבוקש $latex \sqrt{x}$ אינו יכול להיות גדול מההפרש בינהם.
אפשר לנסח זאת כך: אם אתה הולך ברחובות מוסקבה, מסתכל מלפניך ורואה קצין של הק.ג.ב, מסתכל מאחוריך ורואה קצין של הק.ג.ב. - אז לאן שהם הולכים, לך גם אתה.
יישום השיטה: הבנייה נעשית באינדוקציה, החל מ-$latex a_{0}=1$ ו-$latex b_{0}=x$. בשלב ה-$latex n$ נגדיר
$latex \displaystyle (2) \quad ~b_{n+1}:=\frac{a_{n}+b_{n}}{2}\ \ \ \text{-ו} \ \ a_{n+1}:=\frac{x}{b_{n+1}}$
שימו לב ש-$latex b_{n+1}$ הוא הממוצע החשבוני של שני הקירובים הקודמים $latex a_{n}$ ו-$latex b_{n}$, ואילו הממוצע ההנדסי שלהם הוא $latex \sqrt{a_{n}\cdot b_{n}}=\sqrt{x}$ לכל $latex n$.
מכיוון שלכל שני מספרים ממשיים חיוביים $latex a$ ו-$latex b$ מתקיים
$latex \displaystyle ,~a^{2}-2ab+b^{2}~=~(a-b)^{2}~\geq~0$
הרי ש-
$latex \displaystyle ,~(a+b)^{2}~=~a^{2}+2ab+b^{2}~\geq~4ab$
לכן אם נחלק ב-$latex 4$ ונוציא שורש ריבועי נמצא ש-
$latex \displaystyle (3) \quad ,~\frac{a+b}{2}~\geq~\sqrt{ab}$
כלומר, הוכחנו את העובדה הבאה המעניינת כשלעצמה:
משפט: הממוצע החשבוני תמיד גדול או שווה לממוצע ההנדסי (ויש שוויון רק כאשר $latex a=b$).
מכאן נובע (א), כי $latex b_{n+1}:=\frac{a_{n}+b_{n}}{2} \gt \sqrt{a_{n}b_{n}}=\sqrt{x}$, ולכן $latex a_{n+1}:=\frac{x}{b_{n+1}} \lt \sqrt{x}$ לכל $latex n$. אבל אז בוודאי $latex b_{n+1} \lt b_{n}$, כי הממוצע של שני מספרים קטן מהגדול מבינהם; ולכן $latex a_{n+1} \gt a_{n}$ (על-ידי חלוקת $latex x$ באי-השוויון הקודם).
לבסוף, אם $latex b_{n}-\sqrt{x} \lt \varepsilon$, אז
$latex \displaystyle ,~\sqrt{x}-a_{n}=\frac{\sqrt{x}}{b_{n}}(b_{n}-\sqrt{x}) \lt \frac{\sqrt{x}}{b_{n}}\cdot\varepsilon \lt \varepsilon$
ולכן
$latex \displaystyle .~b_{n+1}-\sqrt{x}:=\frac{a_{n}+b_{n}-2\sqrt{x}}{2} \lt \frac{b_{n}-\sqrt{x}}{2} \lt \frac{\varepsilon}{2}$
דוגמא: עבור $latex x=2$ נקבל את הקירובים הבאים ל-$latex \sqrt{2}$:
| $latex b_{0}=$ | $latex 2$ | $latex a_{0}=$ | $latex 1$ |
| $latex b_{1}=\frac{1+2}{2}=\frac{3}{2}=$ | $latex 1.5$ | $latex a_{1}=\frac{2}{b_{1}}=\frac{4}{3}=$ | $latex 1.3333\dotsc$ |
| $latex b_{2}=\frac{3}{4}+\frac{2}{3}=\frac{17}{12}=$ | $latex 1.41666\dotsc$ | $latex a_{2}=\frac{2}{b_{2}}=\frac{24}{17}=$ | $latex 1.4117647\dotsc$ |
| $latex b_{3}=\frac{17}{24}+\frac{24}{34}=\frac{577}{408}=$ | $latex 1.414215686\dotsc$ | $latex a_{3}=\frac{2}{b_{3}}=\frac{816}{577}=$ | $latex 1.414211438\dotsc$ |
| $latex b_{4}=\frac{577}{816}+\frac{816}{1154}=\frac{665857}{470832}=$ | $latex 1.4142135623747\dotsc$ | $latex a_{4}=\frac{2}{b_{4}}=\frac{941664}{665857}=$ | $latex 1.414213562372\dotsc$ |
בקירוב האחרון אנו רואים ש-$latex a_{4}$ ו-$latex b_{4}$ מסכימות עד לספרה ה-$latex 11$ אחרי הנקודה העשרונית - כלומר, ההפרש בינהם קטן מ-$latex 10^{-11}=0.00000000001$. בפרט זה אומר ששתים-עשרה הספרות הראשונות בפיתוח העשרוני של $latex \sqrt{2}$ הן
$latex \displaystyle 1.41421356237$
לוגיקה - לחשוב על החשיבה המתמטית
אנה ליזהטוב
בגיליון נטגר הקודם סיפרנו לכם איך הלוגיקה המתמטית, ענף מתמטי שהיה רדום כאלפיים וארבע מאות שנים, התעורר באמצע המאה התשע עשרה בעבודתו של האנגלי ג'ורג' בול. הלוגיקה המתמטית עושה דבר מוזר ביותר: היא חוקרת את הפעילות המתמטית. כלומר מתארת בצורה פורמלית איך מתמטיקאים חושבים.
"איך חושבים", אתם בוודאי חושבים לעצמכם, היא שאלה ערטילאית. מה זה "איך חושבים"? לגמרי לא ברור. אולי זוהי הסיבה שהלוגיקה הייתה רדומה כל כך הרבה זמן. צריך לפרוט זאת לשאלות קונקרטיות, ובול אכן עשה את הצעד הראשון: הוא הראה איך אפשר לעשות פורמליזציה לטענות מתמטיים פשוטות, שמכילות רק קשרים פשוטים בין טענות, כמו "ו" או "או".
זו הייתה חוליה נוספת בשרשרת של מהפכות שפרויד קרא להן "מהפכות קופרניקאיות", כלומר כאלה שמשנות את תפיסת האדם את עצמו, מראיית עצמו כמרכז היקום להבנה שהוא אינו אלא חלק מן העולם הפיזיקלי, חלק שאולי מעניין במיוחד את עצמו אבל אינו ייחודי כפי שנדמה לו. פרויד הבחין בשלוש מהפכות קופרניקאיות. הראשונה היא הקוסמולוגיה של קופרניקוס עצמו, שהבין שכדור הארץ אינו מרכז היקום בשום מובן אפשרי. השנייה היא תורת האבולוציה של דרווין, שלימד אותנו כי אף אם האדם הוא החבר האינטליגנטי ביותר בממלכת החי, הוא כפוף לאותם חוקים שלהם מצייתים שאר חברי הממלכה. את המהפכה השלישית ייחס פרויד, שמעולם לא סבל מעודף צניעות, לעצמו. תורתו, הפסיכואנליזה, הבהירה שגם בממלכה האחרונה שנותרה לכאורה לשליטתו הבלעדית של האדם, נפשו שלו עצמו, אין הוא מלך יחיד. עמקי נפשו אינם נגישים לו יותר מאשר לסובבים אותו, וייתכן שדווקא את מאווייו שלו הוא מכיר פחות מאשר את העולם החיצוני.
פרויד דיבר לראשונה על מהפכות קופרניקאיות ב-1914, בסדרת הרצאות שנשא באוניברסיטת וינה. אבל באותו זמן כבר החלו לנוע גלגליה של מהפכה רביעית, חשובה עוד יותר משלוש קודמותיה משום שהובילה להמצאת המחשב. זו הייתה התובנה שאפילו הדבר שנראה ייחודי מכל לאדם - החשיבה המופשטת, אינה אלא חלק מן העולם הפיזיקלי. מאמצע המאה התשע- עשרה החלה לחלחל ההבנה שגם החשיבה המופשטת אינה אלא תהליך פיזיקלי, כמו תנועתם של גופים או זרימה של מים. אפשר לתאר אותה במונחים מכאניים, והיא יכולה להיות גם נחלתה של מכונה.
באופן לא מפתיע, זרעיו של המפנה נזרעו באנגליה של המהפכה התעשייתית. בעקבות ניצחונן המוחץ של המכונות החלו הוגים לייחס מכאניוּת לכל תופעות העולם, ובהן האנושיות. מקצת ההוגים היו תיאורטיקנים, כמו קרל מרקס, שהחיל מושגים דטרמיניסטיים על תהליכים חברתיים, והיו גם שניסו ליישם זאת בפועל. המפורסם שבהם היה צ'רלס בבג' ($latex Charles ~~Babbage$), שנהוג לייחס לו את הבנייה (על הנייר) של המחשב הראשון. ב-1820 הוא פירסם תוכנית לבנייתה של מכונת חישוב שיתרונה הגדול הוא שהיא ניתנת לתכנות, ואפילו השיג מימון ממשלתי להרכבתה. את מלאכת ההרכבה המעשית לא השלים מעולם, אבל בסוף המאה העשרים הושלמה המלאכה במוזיאון המדע הבריטי, והתברר שבבג' לא רימה. המכונה פעלה.
את ניצחונה הגדול ביותר נחלה המהפכה המחשבתית הזאת דווקא במתמטיקה. החשיבה המתמטית היא המופשטת ביותר מבין סוגי החשיבה, אבל גם המאורגנת ביותר, ולכן אפשר לחקור אותה בצורה מתמטית. כאמור, הראשון שעשה זאת בצורה שיטתית היה ג'ורג' בול. הוא הראה איך לעשות פורמליזציה של טענות מתמטיות. ואכן, טענות מתמטיות הן לבני הבניין שמהן בונים מגדלים מתמטיים. אבל לבנים עדיין אינן יוצרות בית. נחוץ מלט שיחבר אותן למבנים בעלי משמעות. את התפקיד הזה ממלאות ההוכחות. הוכחות הן גולת הכותרת של הפעילות המתמטית. הן מוודאות מה נכון, אבל חשוב מכך, הן עדות להבנה. "הוכחה לא נועדה להראות לנו שמשפט מתמטי הוא נכון. כוונתה להראות לנו למה הוא נכון," אמר המתמטיקאי האמריקני רלף בואז $latex (Ralph ~Boas)$.
היה זה פילוסוף-מתמטיקאי גרמני בשם גוטלוב פְרֶגֶה $latex (Gottlob~~ Frege)$ שעשה את הצעד האמיץ הבא: להראות שגם הוכחות אפשר לחקור בצורה מתמטית-פורמלית. הדבר הראשון שפרגה עשה היה להעשיר את השפה המתמטית. הוא הוסיף סימן ל"לכול". הסימון שלו הוחלף מאז, וכיום משתמשים בסימון $latex \forall$, שהוא $latex A$ הפוכה, ונגזר מן המילה "$latex All$", או "$latex Alles$" הגרמני. למשל, $latex \forall x(x \ge 0)$ אומר ש"כל מספר גדול או שווה מ-$latex 0$" – טענה נכונה במספרים הטבעיים. מאוחר יותר הוכנס גם סימון ל"קיים" – $latex \exists$, היפוכה של $latex E$, הגזורה מ-$latex Exists$. למשל, $latex \exists x(x \lt 1)$ אומר "קיים מספר קטן מ-$latex 1$" (שוב, טענה נכונה במספרים הטבעיים, משום שאכן קיים מספר כזה, הלוא הוא 0).
בשפה החדשה אפשר להביע כל טענה מתמטית מוכרת, ומכאן היה פרגה יכול להמריא למשימה הבאה: הגדרה מהי הוכחה. כל מי שראה מימיו הוכחות מתמטיות מכיר את התכונה העיקרית שלהן: הליניאריות. הן בנויות לבנה על גבי לבנה. זו היתה הגדרתו של פרגה ל"הוכחה":
הוכחה היא סדרה של טענות, שכל אחת נובעת מאלה שהופיעו לפניה.
בכך אין חידוש גדול. האופי הנדבכי של הוכחות הוא כאמור עניין ידוע. תגליתו המפתיעה של פרגה היתה ש"נביעה" היא מושג פשוט. משחק ההוכחה אינו כה מסובך כפי שנדמה. הוא מתנהל בסך הכול על פי שני כללים. הכלל הראשון, שניסח כבר אריסטו, נקרא "ניתוק רישא". אם בסדרת הטענות שמרכיבות את ההוכחה מופיעה, למשל, הטענה "אם היום יום שלישי, אז יורד גשם", ומופיעה גם הטענה "היום יום שלישי", אתם יכולים להוסיף בבטחה לסדרה את הטענה "יורד גשם". אם הוכחתם "אם א' אז ב'" וגם הוכחתם את א', הרי הוכחתם את ב'.
הכלל השני אינו מסובך יותר, אבל הוא מפתיע במקצת. הוא נקרא "הכללה", והוא אומר כך: נניח שהוכחתם ש-"יוסי הוא בן תמותה", ונניח שלא השתמשתם בשום תכונה מיוחדת של יוסי מלבד היותו בן אדם. אם עשיתם זאת, הוכחתם בעצם שכל אדם הוא בן תמותה. הרי ההוכחה תקפה לכל אדם. בניסוח פורמלי, הכלל הוא זה:
אם בסדרת הטענות שמהווה הוכחה הגעתם לתכונה כלשהי (נקרא לה $latex P$) של עצם $latex x$, הרי אתם רשאים להוסיף לסדרת הנוסחאות נוסחה חדשה, שגם היא הוכחה בזאת: "לכל $latex x$ מתקיימת התכונה $latex P$", ובסימון המתמטי – $latex \forall x P$.
למעשה, מבחינתנו לא חשוב מהם בדיוק כללי ההוכחה, אלא רק שהם פשוטים וספורים. פירוש הדבר הוא שמשחק ההוכחה פשוט מאוד. אם מגיע אליכם אדם ובידיו סדרת טענות שהוא אומר כי היא הוכחה, קל מאוד לבדוק זאת. לבנות הוכחה – זה כבר סיפור אחר. קל יותר לזהות עצם כ"מחט", לאחר שהציגו אותו בפניכם, מאשר למצוא את המחט בערמת שחת.
כל אחד משני כללי ההיסק – ניתוק הרישא וההכללה – מוכיח נוסחאות על פי נוסחאות קודמות. אבל לא די בכך. כדור הארץ עומד כידוע על גבו של צב – אבל על מה עומד הצב? הרי צריך להתחיל ממקום כלשהו, מטענות שאינן נובעות מטענות קודמות. אלה הן האקסיומות, הנחות מוצא שעל יסודותיהן אפשר לבנות את הבניין. פרגה הגדיר כמה אקסיומות בסיסיות, שנכונות בכל תחום. למשל, "אם היום יום שלישי אז היום יום שלישי", או בצורה פורמלית $latex \alpha \rightarrow \alpha$. "כל דבר גורר את עצמו". או כלל אחר: אם לא נכון שלא נכון שהיום יום שלישי, אז היום יום שלישי. "לא לא" משמעו "כן", ובניסוח פורמלי: $latex \sim\sim \alpha \rightarrow \alpha$. שפירושו "אם לא נכון שלא $latex \alpha$ אז $latex \alpha$ נכונה".
נוסף על האקסיומות הכלליות, לכל תחום מתמטי יש האקסיומות המיוחדות לו. בגיאומטריה, למשל, האקסיומות יהיו טענות כמו "דרך כל שתי נקודות עובר רק קו ישר אחד" (את המילים האלה צריך לתרגם, כמובן, לנוסחאות). בתורת המספרים, כל מערכת אקסיומות סבירה תכיל בוודאי את האקסיומה שאם מוסיפים 0 למספר, הוא לא משתנה, ופורמלית - $latex \forall x (x+0=x)$. הגדרתו של פרגה להוכחה היא אפוא זו: הוכחה היא סדרת נוסחאות שכל אחת מהן היא או אקסיומה, או נובעת על פי אחד משני כללי ההיסק מנוסחאות קודמות. להשלמת ההגדרה נחוץ לומר עוד דבר אחד: מה מוכיחה סדרת הנוסחאות הזאת? פשוט: את הנוסחה האחרונה שבה, את "שורת המחץ".
הרעיונות החדשים של פרגה היו כה מהפכניים, שאף אחד לא התייחס אליהם ברצינות. מישהו אחד שכן התייחס היה גיאורג קנטור, מהפכן בעצמו, שבנה במו ידיו את תורת הקבוצות המודרנית. הוא כתב על ספרו של פרגה מאמר קטילה. פרגה נעשה מר נפש ומסוגר. באחרית ימיו גם לקה באנטישמיות קשה (ייתכן שהיה לכך קשר לעובדה שקנטור היה יהודי). למזלה של המתמטיקה, הייתה לברטראנד ראסל האגלי בילדותו אומנת גרמנייה, ובזכותה הוא ידע גרמנית. כך הגיע, כעשרים שנים מאורח יותר, לקרוא את כתביו של פרגה. הוא הבין את חשיבות המהפכה החדשה, ופרסם אותה דרך ספר שכתב עם ידידו ומורו וויטהד ($latex Whitehead$). הספר, שנקרא "עקרונות המתמטיקה" ($latex Principia ~Mathematica$), היה נקודת מפנה. מאותו רגע הפכה הלוגיקה המתמטית לענף מרכזי. וזה היה פתח למהלכים מרחיקי לכת, שבסופו של דבר הובילו להמצאת המחשב.
חידות
דניאל לובזנס
לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 24.12.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.
חידה 1 –איך לחלק את העוגה המשולשת?
אורה ובני מחלקים ביניהם עוגה (שניתן להניח כי היא בגובה ומרקם אחיד, כך שכל אחד רוצה לקבל שטח גדול יותר של העוגה) לפי הכלל הבא: אורה בוחרת נקודה כלשהיא על גבי העוגה, ובני רשאי לחתוך את העוגה בקו ישר העובר דרך הנקודה שסימנה אורה אח"כ בני בוחר לעצמו את אחד החלקים והשני ניתן לאורה. בני ואורה בוחרים את מיקום הנקודה וכוון הקו כדי לקבל מקסימום משטח העוגה.
ברור שאם העוגה עגולה, הבחירה של אורה היא מרכז העיגול, וכל קו שיעביר בני יבטיח לו בדיוק חצי מהעוגה וגם אורה תקבל חצי עוגה.
החידה היא מה קורה כשלעוגה צורת משולש? מהי הנקודה הטובה ביותר שתבחר אורה? איך יעביר בני את קו החיתוך? בהנחה ששניהם עושים את הבחירות הטובות ביותר, איזה חלק מהעוגה יקבל בני ואיזה יישאר לאורה?
חידה 2–איך ליצור רבוע מרבוע ומשולש?
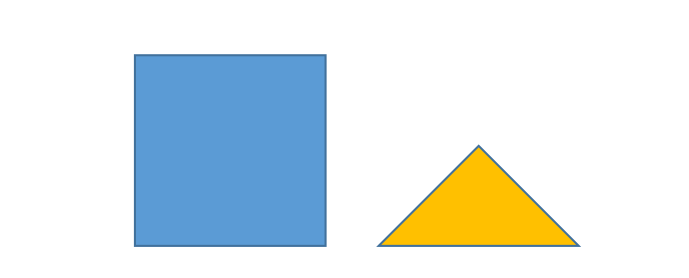
נתון ריבוע ומשולש ישר זווית ושווה שוקים הקטן בשטחו משטח הרבוע. איך ניתן לחתוך את הרבוע ל3 חלקים ע"י קוים ישרים, ואת המשולש ל2 חלקים ע"י קו ישר אחד, ומחמשת החלקים להרכיב ריבוע?
חידה 3– מה הדרך הקצרה של הנמלה לטיפת הדבש?

נתונה כוס זכוכית בעלת צורה גלילית, בקוטר 8 ס"מ ובגובה 8 ס"מ. על התחתית סמוך לדופן, בתוך הכוס, יש טיפת דבש. מחוץ לכוס, סמוך לתחתית, בנקודה המרוחקת ביותר מטיפת הדבש נמצאת נמלה. מה הדרך הקצרה ביותר של הנמלה לטיפת הדבש? מה אורכה?
רמזים לחידות מגיליון נובמבר 2015
חידה 1 – איך לחלק את המחרוזת?
חברו את המחרוזת בקצותיה ליצירת מעגל. השתמשו בשיטה דומה לזו של הוכחת המקרה החד ממדי של משפט בורסוק-אולם המופיע במאמרו של רון אהרוני בגיליון אוקטובר 2015.
חידה 2– איך למצוא את הדרך הנכונה?
יש למצוא דרך שהשאלה "תעבור" פעמיים דרך שני משיבים.
חידה 3– סידור אבני דומינו?
כמה פעמים מופיע כל מספר?
פתרון החידות גיליון אוקטובר 2015
חידה 1 –שמיכת טלאים
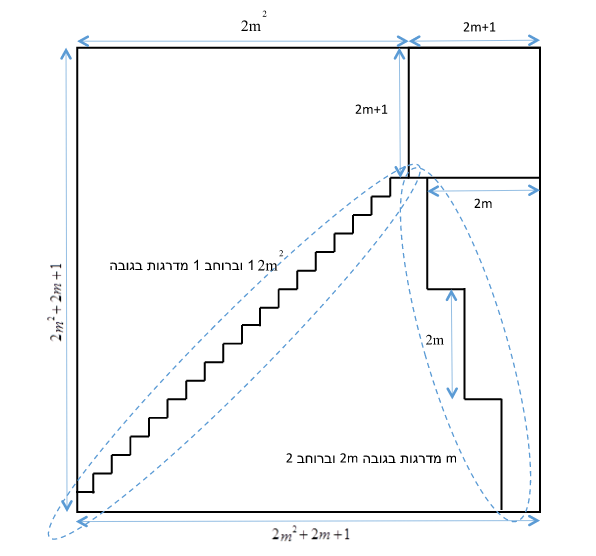
הפתרון לחידה – שימו לב לשלשה הפיתגוריאנית $latex 13^2 = 12^2 + 5^2$

אם היה אפשרי לפתור את החידה ע"י חלוקת הרבוע הגדול ל 3 חלקים בלבד, הרי שבחלק אחד תהינה 2 פינות של הרבוע הגדול שהמרחק (האנכי או האופקי) ביניהן הוא 13 בעוד ברבוע הנוצר לאחר החלוקה המרחק המקסימלי הוא 12. תנו דעתכם שבבעיה זו ניתן לסובב את החלקים החתוכים בכפולות של 90 מעלות בלבד.
את הפתרון ניתן להכליל לכל השלשות הפיתאגוריאניות מהצורה:
$latex \displaystyle (2m^2 + 2m)^2 + (2m+1)^2 = (2m^2 + 2m + 1)^2$
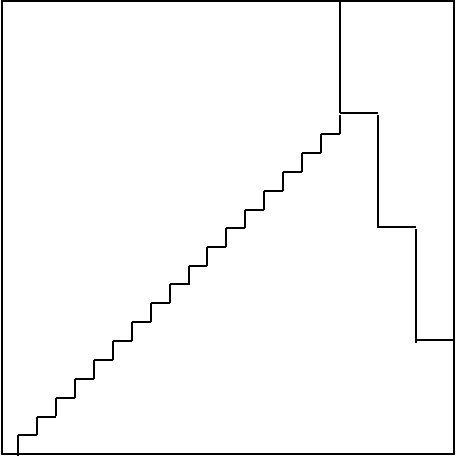
השרטוטים הבאים מתארים את חלוקת הרבוע הגדול והרכבת רבוע שאורך צלעו קטן ב 1 משלשה החלקים.
חידה 2–איזו ספרה חסרה?
נחשב את המספר מודולו 9.
קל לראות:
$latex 2^2 = 4 \pmod{9}$
$latex 2^4 = 7 \pmod{9}$
$latex 2^8 = 4 \pmod{9}$
$latex 2^{16} = 7 \pmod{9}$
מאחר ו: $latex 2^{29} = 2^{16} \cdot 2^8 \cdot 2^4 \cdot 2^1 = 7 \cdot 4 \cdot 7 \cdot 2 = 5 \pmod{9}$ ונתון שבתוצאה מופיעות כל הספרות פרט לאחת – הספרה החסרה היא 4 (סכום כל הספרות 1..9 הוא 0 מודולו 9).
חידה 3– איזה מספרים ניתן לרשום כסכום של רצף של מספרים טבעיים?
להלן פתרונו של עומר שמחי (בתיקונים קלים):
פתרון: כל מספר שאינו חזקה אי שלילית של 2.
הוכחה: ראשית נשים לב כי אם מספר הוא סכום של רצף טבעיים (לפחות שניים) אזי הוא מהצורה:
$latex M = k + (k+1) + \dots + (k+n-1)$
כאשר $latex k$ הוא המספר הטבעי הראשון ועוד $latex n-1$ מספר החוברים ברצף.
קל לראות מסכום סדרה חשבונית ש:
$latex \displaystyle d = 1, a_1 = k \Rightarrow M = \frac{n \cdot (2k + 1 \cdot (n-1))}{2} = \frac{n \cdot (n + (2k-1))}{2}$
ראשית נראה כי כל מספר אי זוגי $latex M$ (שאינו 1 כמובן) ניתן להצגה כסכום רצף טבעיים:
$latex n=2 \Rightarrow M = 2k + 1, \forall k \in \mathbb{N}$ וזהו ביטוי לכל מספר אי זוגי גדול מאחד כמובן.
כעת נראה כי אם $latex M = 2^r, \forall r \in \mathbb{N} \cup \{0\}$ לא ניתן לבטא כסכום כנ"ל:
נשווה: $latex 2^r = \frac{n \cdot (n + 2k - 1)}{2}$
אולם אם $latex n (\gt 2)$ אי זוגי אזי נקבל סתירה כי אז לחזקה של 2 אמור להיות מחלק אי זוגי גדול מ1, ואם $latex n$ זוגי אזי $latex n + 2k-1$ אי זוגי ושוב סתירה מאותה סיבה.
לכן חזקה טבעית של 2 או המספר 1 לא ניתנים לייצוג כנ"ל.
כעת נותר להוכיח שכל זוגי שאינו חזקה של 2, דהיינו: $latex M = 2^r t, t \equiv 1 \pmod{2}, r \in \mathbb{N}$ ניתן להצגה.
כלומר, נחפש $latex n$ ו $latex k$ כך ש: $latex 2^r t = \frac{n \cdot (n + 2k - 1)}{2} \Leftrightarrow 2^{r+1} t = n \cdot (n + 2k - 1)$
כעת, נפריד לשני מקרים:
(1): $latex t \gt 2^{r+1}$:
נציב: $latex n = 2^{r+1} \Rightarrow t = n + 2k - 1 = 2^{r+1} + 2k - 1$
היות ש$latex k$ ניתן לבחירה חופשית, הרי שכל אי זוגי $latex t$ שמקיים את תנאי אי השיוויון כמובן יתקבל בצורה כזו.
(2): $latex t \lt 2^{r+1}$:
נבחר: $latex n = t \Rightarrow 2^{r+1} = n + 2k - 1= 2k + t -1 $
ושוב היות ש$latex t$ אי זוגי ו$latex k$ ניתן לבחירה חופשית נקבל שוב שאפשר לקבל כל חזקה של 2 שמקיימת את אי השוויון בצורה כזו בבחירה מתאימה של $latex k$.
מש״ל.
שמות הפותרים נכונה את החידות מגיליון נובמבר 2015
תומר שני, חניתה, בי"ס סולם צור כתה י"ב – כל החידות!