נטגר גליון 4
דבר העורך
רון אהרוני
זהו גיליון רביעי, מקוצר מעט בגלל חופשת פסח.
מה יש לנו הפעם? ראיון עם מריה צ'ודנובסקי, מתמטיקאית שאת תאריה הראשון והשני עשתה בטכניון. זו תהיה הזדמנות לעשות היכרות קטנה עם תחום המחקר שלה, תורת הגרפים.
המתמטיקה מתחלקת באורח גס לארבעה תחומים: אלגברה, שבה חוקרים פעולות בין איברים, שמצייתות לחוקים קשוחים ומוגדרים היטב; האנליזה, או כפי שאתם מכירים אותה מבית הספר - החשבון הדיפרנציאלי, שעוסק במושג הגבול; הגיאומטריה; ולבסוף "מתמטיקה דיסקרטית", או "קומבינטוריקה". האחרון הוא לכאורה התחום הפשוט ביותר - הוא עוסק בקבוצות (בדרך כלל סופיות), וביחסים שמוגדרים על איבריהן - אין פעולות ואין גבולות, לפחות לא בהגדרה של הבעיות. עם זאת התחום הזה התפתח בקצב מהיר ביותר בחמישים השנים האחרונות, בין השאר עקב הקשר שלו למדעי המחשב. תורת הגרפים היא לכאורה התחום הפשוט ביותר בתוך הקומבינטוריקה: היא עוסקת ביחסים שמוגדרים רק בין זוגות של איברים (אפשר להגדיר גם יחסים בין שלשות: היחס $latex {a+b=c}$ הוא יחס בין שלשה של מספרים. אפשר להגדיר גם יחסים בין רביעיות וחמישיות - מכירים יחסים כאלה?) ובכל זאת - זהו תחום מורכב ועמוק ויש בו בעיות קשות מאוד.
עוד יהיה בגיליון מאמר שנוגע בהתפתחויות מסעירות אחרונות בתורת המספרים - עוד תחום שבו קל מאוד לנסח השערות שהן לפעמים קשות ביותר להוכחה. הפעם מדובר בהשערת הראשוניים התאומים - יש אינסוף זוגות של ראשוניים תאומים, כלומר כאלה שההפרש ביניהם הוא $latex {2}$ - למשל $latex {101,103}$ הוא זוג כזה. אין איש מפקפק בנכונות ההשערה הזאת, אבל ההתקדמות בה אטית. לאחרונה הייתה פריצת דרך, ומאמרו של יוסי כהן ינסה להסביר מעט על הכלים ששימשו לכך.
מאמר אחר ישלים סדרה של מאמרים על שברים עשרוניים אינסופיים, ויוכיח בעזרתם עובדה מפתיעה על מספרים. לעובדה הזאת יינתנו עוד שתי הוכחות, ששתיהן משתמשות בעיקרון ידוע שנקרא "עקרון שובך היונים" - אם תכניסו $latex {101}$ יונים ל-$latex {100}$ תאים, יצטרכו שתי יונים להצטופף באותו תא. עיקרון פשוט מאוד, אבל בעל אינספור שימושים מעניינים. האתגר בשימוש בו הוא למצוא את ההגדרה הנכונה של ה"תאים".
כמו כן תהיה, כרגיל, בעיה לגדולים - הפעם בעיה גיאומטרית, וכן בעיות לקטנים.
בברכת הנאה,
מצוות העיתון
ראיון עם מריה צ'ודנובסקי
נטגר
מריה צ'ודנובסקי היא מהבולטים בין אנשי הקומבינטוריקה הצעירים בעולם. יחד עם סימור, רוברטסון ותומס היא פתרה את ההשערה שהייתה עד אז המפורסמת ביותר בתורת הגרפים, "השערת הגרף המושלם". מאז נוספו עוד כמה בעיות מרכזיות לרשימת הבעיות שפתרה. את לימודי התואר הראשון והתואר השני עשתה בטכניון, את הדוקטורט באוניברסיטת פרינסטון, וכיום היא חברת סגל באוניברסיטת קולומביה בניו יורק.
תחום עבודתה של מריה הוא תורת הגרפים המבנית. כדי להבין את המילים האלה, יש לדעת תחילה מהו גרף: זהו אוסף זוגות מתוך קבוצה נתונה של איברים שנקראים "קדקוקדים". למשל, אוסף שלושה הזוגות $latex {ab,~bc,~ac}$ הוא גרף. הזוגות בגרף נקראים "צלעות". משמעות השם "גרף" ביוונית היא פשוט "ציור". הסיבה לשם היא שזוגות אפשר לצייר על ידי קווים - למשל, את הגרף שלעיל אפשר לצייר כשלוש נקודות במישור, עם שלושה קטעים שמחברים ביניהן - זהו פשוט משולש. עכשיו אתם מבינים בוודאי מניין המילה "צלעות"!
לכאורה - גרפים הם דבר פשוט. בסך הכל אוסף זוגות - מה כבר אפשר לומר על מבנה כה פשוט? ובכן, זה תלוי במושגים שחוקרים. יש מושגים מורכבים על זוגות. חישבו על החיים: בני אדם משתדכים בזוגות, וזה לפעמים לא פשוט!
אחד המושגים המפורסמים ביותר על גרפים הוא "צביעה". צביעה של גרף היא צביעה של הקדקודים שלו, כך שכל שני קדקודים שמחוברים בצלע צבועים בצבעים שונים. מספר הצביעה של גרף הוא המספר הקטן ביותר של צבעים שמספיקים לצביעתו. למשל, ברור שמספר הצביעה של המשולש הוא $latex {3}$. נחוץ צבע נפרד לכל קדקוד. מספר הצביעה מסומן באות היוונית $latex {\chi}$ - זוהי ה"חת" היוונית, ומקור הסימון הוא "חרומו", שהיא המילה היוונית ל"צבע" (מקובל יותר לכתוב "כרומו", אבל ה"כף" צריכה להיות לא דגושה. לפחות על פי ההיגוי היווני).
קליק בגרף ("קליקה" פירושה אגודה) הוא קבוצת קדקודים שכולם מחוברים בצלעות. למשל, המשולש הוא קליק. כולם בו מחוברים. ברור שאם בגרף יש קליק בגודל $latex {k}$ אז נחוצים לפחות $latex {k}$ צבעים לצביעתו: כל אחד מקדקודי הקליק ידרוש צבע שונה. לא ייתכנו שני קדקודים באותו צבע, כי הרי כל שני קדקודים בקליק מחוברים. מספר הקליק של גרף הוא גודל הקליק המקסימלי. הוא מסומן ב-$latex {\omega}$ - האות האחרונה באלף בית היווני (אין לי מושג מה מקור הסימון הזה). ובכן, מה שאמרנו זה עתה הוא שבכל גרף מתקיים
$latex \displaystyle \chi \ge \omega.$
יש גרפים שבהם אי השוויון הזה הוא חד. למשל - מחומש:
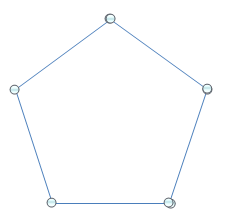
כאן $latex {\omega=2}$ בעוד ש-$latex {\chi=3}$ (בדקו מדוע!)
למעשה, בכל מעגל אי זוגי $latex {\omega=2}$ ו-$latex {\chi=3}$. גרף נקרא מושלם אם מתקיים בו $latex {\omega=\chi}$. ובכן - לא בדיוק. דורשים זאת לא רק לגרף עצמו אלא גם לכל תת גרף מושרה, כלומר גרף שמתקבל מלקיחת חלק מן הקדקודים, עם כל הצלעות בגרף המקורי שמחברות את הקדקודים שלקחנו.
דוגמאות לגרפים מושלמים: מעגל זוגי הוא מושלם. גרף שאין בו מעגלים בכלל הוא מושלם. כך גם כל גרף שמורכב משתי קבוצות $latex {A}$ ו-$latex {B}$ של קדקודים, כשכל צלע בגרף מחברת קדקוד ב-$latex {A}$ עם קדקוד ב-$latex {B}$ כלומר אין צלעות בתוך $latex {A}$ וצלעות בתוך $latex {B}$ - גרף כזה נקרא "דו צדדי".
המשלים של גרף הוא הגרף המתקבל מלקיחת כל הזוגות שאינם נמצאים בגרף המקורי. למשל, המשלים של משולש הוא הגרף עם שלושה קדקודים, בלי צלעות בכלל. המשלים של מעגל באורך $latex {4}$ הוא גרף עם $latex {4}$ קדקודים, ושתי צלעות זרות.  המשלים של מחומש הוא הגרף המורכב מכל אלכסוני המחומש. האם אתם יכולים להבחין בכך שזהו בעצם גם כן מחומש, רק מצויר קצת אחרת?
המשלים של מחומש הוא הגרף המורכב מכל אלכסוני המחומש. האם אתם יכולים להבחין בכך שזהו בעצם גם כן מחומש, רק מצויר קצת אחרת? 
בשנת $latex {1978}$ הוכיחו שני מתמטיקאים, לובס ופלקרסון, בנפרד, את המשפט הבא:
משפט 1 גרף הוא מושלם אם ורק אם המשלים שלו הוא מושלם.
בכך הם פתרו את מה שנקרא אז "השערת הגרף המושלם החלשה". בצידה הייתה השערה חזקה יותר, של המתמטיקאי הצרפתי $latex {Berge}$. זוהי ההשערה שהוכיחו מריה וחבריה, ואם כן היא עכשיו משפט - "משפט הגרף המושלם":
משפט 2 גרף הוא מושלם אם ורק אם הוא אינו מכיל כתת גרף מושרה מעגל אי זוגי מאורך $latex {5}$ או יותר, או משלים של מעגל כזה.
המשפט הזה שייך לתורת הגרפים המבנית. בתורה הזאת מאפיינים תכונות של גרפים על ידי תת מבנים אסורים - למשל, תת גרפים מושרים אסורים, כמו במשפט הגרף המושלם. זוהי תורה ענפה, וקשה.
אבל בואו נעזוב בזאת את הגרפים, ונפנה לראיון עם מריה.
נטגר: סיפרת שכילדה בסנט פטרסבורג למדת בבית ספר מיוחד למתמטיקה. איזה חלק הוא מילא בקריירה שלך?
מריה: בית הספר לימד אותי הרבה דברים, שאחד החשובים בהם היה שהמתמטיקה יפה. זה עורר את סקרנותי, וגרם לי להתעניין ללמוד עוד. כילדה בת $latex {13}$ למדתי לוגיקה ופעולות על קבוצות, במיוחד קבוצות אינסופיות. המורה אמר לנו שיש סוגים שונים של אינסוף. זה היה כל כך מסתורי ויפה, שציפיתי בכליון עיניים לגדול וללמוד למה הכוונה. אחר כך למדתי בחוג בטכניון, שבו למדתי עוד דברים יפים, ששכנעו אותי שאני רוצה להיות מתמטיקאית.
נטגר: האם הורייך דחפו אותך?
מריה: הורי היו תמיד תומכים. הם שיבחו אותי על ציונים טובים, אבל לא היו דוחפניים. יכולתי תמיד לבחור מה לעשות מחוץ לבית הספר, ואף פעם לא לחצו עלי לעשות שיעורי בית.
נטגר: האם חשוב להתחיל בגיל צעיר?
מריה: נדמה לי שכן, אבל בוודאי לא כמו בספורט או במוזיקה, שבהם הזיכרון של השרירים קובע הרבה.
נטגר: האם עשית משהו מחוץ ללימודים - למשל נגינה בכלי?
מריה: הייתי בחוג של מדעי המחשב, אבל זה לא שונה מאוד ממתמטיקה. היו לי חיי חברה, אבל לא התעניינתי בשום דבר באותה מידה כמו במתמטיקה. למדתי פסנתר, אבל אחרי חמש שנים היה ברור שאו שאני עוזבת או שהמורה עוזבת…
נטגר: האם את מעדיפה לעבוד לבד או בצוות?
מריה: אני אוהבת לעבוד עם אנשים. כשעובדים לבד, צריך להתקדם הרבה לפני שלאנשים יהיה עניין לדבר אתך על הנושא. כשעובדים יחד, כל התקדמות מעניינת את כל המשתתפים. דרך העבודה האהובה עלי היא לחשוב לבד, לדון בעניינים עם חברי לעבודה, ואז לחזור שוב לחשוב לבד.
נטגר: האם את מעדיפה מתמטיקה אלמנטרית או עם מושגים מורכבים?
מריה: אני מעדיפה מתמטיקה אלמנטרית. אני רוצה לדעת את הכל על הנושא שאני חוקרת מהתחלה עד הסוף - בצורה הקונקרטית ביותר.
נטגר: מהי הבעיה שהיית רוצה יותר מכל לפתור כיום?
מריה: ההשערה שמעניינת אותי ביותר כיום היא השערת ארדש-היינל. בקווים כלליים היא אומרת שלכל גרף קטן - נאמר על $latex {6}$ קדקודים, אם אוסרים אותו כגרף מושרה של גרף גדול (נקרא לו "הגרף האב"), אז הגרף האב מתנהג בצורה מאוד לא מקרית. ליתר דיוק: הגרף האב חייב אז להכיל קליק גדול, או משלים של קליק גדול. "גדול", כמובן, הוא ביחס למספר הקדקודים של הגרף האב.
תודתנו נתונה למריה שהסכימה להתראיין.
הנפה של ארטוסטנס-לז'נדר
יוסי כהן
כמו לא מעט בעיות בתורת המספרים גם בהשערת התאומים הראשוניים יש פער מביך בין קלות הניסוח של ההשערה וקושי ההוכחה שלה. ההשערה גורסת שקיימים אינסוף זוגות ראשוניים שההפרש ביניהם הוא 2.לאחרונה הושגה התקדמות מרשימה בבעיה זו. הכלי שבעזרתו הושגה ההתקדמות הזאת נקרא "שיטות נפה" – נפה (פא רפויה) היא כברה, ובלשון פשוטה יותר – מסננת.
שיטות נפה הן שיטות שמנפות מקבוצה מסוימת של טבעיים את הטבעיים הבעייתיים, מנפה - בדיוק כמו שעושה כל נפה, יחד עם זאת, אחר כך השיטה גם יודעת להעריך את המספר המנופה. נביא להלן שתי דוגמאות משיטת הנפה של ארטוסתנס. (276 – 194- לפנה"ס מתמטיקאי, גאוגרף ואסטרונום יווני)
א. נסתכל על כל המספרים מ- 1-100 בטבלה
|
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
|
20 |
19 |
18 |
17 |
16 |
15 |
14 |
13 |
12 |
11 |
|
30 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
|
40 |
39 |
38 |
37 |
36 |
35 |
34 |
33 |
32 |
31 |
|
50 |
49 |
48 |
47 |
46 |
45 |
44 |
43 |
42 |
41 |
|
60 |
59 |
58 |
57 |
56 |
55 |
54 |
53 |
52 |
51 |
|
70 |
69 |
68 |
67 |
66 |
65 |
64 |
63 |
62 |
61 |
|
80 |
79 |
78 |
77 |
76 |
75 |
74 |
73 |
72 |
71 |
|
90 |
89 |
88 |
87 |
86 |
85 |
84 |
83 |
82 |
81 |
|
100 |
99 |
98 |
97 |
96 |
95 |
94 |
93 |
92 |
91 |
ונניח שאני מעוניין למצוא את כל הראשוניים בטבלה זו, כלומר את כל הראשוניים עד 100. נמחק את כל הכפולות של הראשוני הראשון 2 (חוץ מ-2 כמובן).
|
9 |
7 |
5 |
3 |
2 |
1 |
||||
|
19 |
17 |
15 |
13 |
11 |
|||||
|
29 |
27 |
25 |
23 |
21 |
|||||
|
39 |
37 |
35 |
33 |
31 |
|||||
|
49 |
47 |
45 |
43 |
41 |
|||||
|
59 |
57 |
55 |
53 |
51 |
|||||
|
69 |
67 |
65 |
63 |
61 |
|||||
|
79 |
77 |
75 |
73 |
71 |
|||||
|
89 |
87 |
85 |
83 |
81 |
|||||
|
99 |
97 |
95 |
93 |
91 |
אם נמחק כעת באופן דומה את כל הכפולות של 3 חוץ מ-3, את של 5 חוץ מ-5 ואת של 7 חוץ מ-7 נקבל
|
7 |
5 |
3 |
2 |
1 |
|||||
|
19 |
17 |
13 |
11 |
||||||
|
29 |
23 |
||||||||
|
37 |
31 |
||||||||
|
47 |
43 |
41 |
|||||||
|
59 |
53 |
||||||||
|
67 |
61 |
||||||||
|
79 |
73 |
71 |
|||||||
|
89 |
83 |
||||||||
|
97 |
ולמעשה קבלנו את כל הראשוניים עד 100. ברור שמספיק לסנן את הקבוצה מראשוניים על השורש של 100 שהוא 10. אם מספר עד 100 לא ראשוני יש לו בוודאי מחלק ראשוני שקטן משורש 100 (אחרת אם כל המחלקים שלו גדולים משורש 100 נקבל שמכפלת המחלקים גדולה מ-100. סתירה)
ב. שיטה זו לא רק טובה למציאת ראשוניים אלא בכלל לסינון קבוצה של מספרים טבעיים מהטבעיים שיש להם מחלק קטן. כלומר נוכל למצוא בעזרת שיטה זו גם את כל הטבעיים בעלי מחלקים ראשוניים "גדולים". למשל, אם ניקח את קבוצת כל השלמים עד 256 נניח ונסנן מהם בשיטת ארטוסתנס את כל הראשוניים עד שורש שלישי של 350 כלומר עד 7 (כולל) נקבל ברשימה שנותרה את כל השלמים עד 256 שיש להם מחלקים ראשוניים הגדולים מ-7 (~שורש שלישי של 350)
|
13 |
11 |
|||||||||||||
|
31 |
29 |
23 |
19 |
17 |
||||||||||
|
47 |
43 |
41 |
37 |
|||||||||||
|
61 |
59 |
53 |
||||||||||||
|
79 |
73 |
71 |
67 |
|||||||||||
|
89 |
83 |
|||||||||||||
|
109 |
107 |
103 |
101 |
97 |
||||||||||
|
127 |
121 |
|
113 |
|||||||||||
|
143 |
139 |
137 |
131 |
|||||||||||
|
157 |
|
149 |
||||||||||||
|
173 |
169 |
167 |
163 |
|||||||||||
|
191 |
187 |
|
181 |
|
||||||||||
|
|
199 |
197 |
193 |
|||||||||||
|
223 |
221 |
|
211 |
209 |
||||||||||
|
239 |
233 |
229 |
227 |
|||||||||||
|
253 |
251 |
247 |
241 |
עד עכשיו הצגנו את הקונספט של ארטוסתנס למציאת ראשוניים, וטבעיים בעלי מחלקים ראשוניים "גדולים". השאלה החשובה ולמעשה העיקרית היא איך בכלל אפשר לספור את הקבוצות הללו. מסתבר שלספור ראשוניים בצורה כזו זה לא כל-כך פשוט אולם לספור טבעיים בעלי מחלקים ראשוניים גדולים או לפחות לתת הערכה של מספר כזה זה אפשרי גם אפשרי.
פונקציית מביוס
כלי שמשמש לעשות זאת נקרא "פונקציית מביוס". הפונקציה הזאת מסומנת באות היוונית $latex { \mu }$ ("מו", שהיא ה"מם" היוונית, האות הראשונה בשמו של מביוס , 1790 - 1868, מתמטיקאי ואסטרונום גרמני, תלמידו של גאוס. על שמו גם נקראת "טבעת מביוס")
לשם כך, נצטרך לעשות הכרה עם פונקציה אריתמטית (=פונקציה שמקבלת ערכים טבעיים בלבד) הידועה בשם פונקציית מביוס - $latex { \mu }$. לצורך זה נגדיר מספר טבעי חסר-ריבועים כמספר שכל המחלקים הראשוניים שלו שונים. למשל המספר $latex { 3\cdot2=6 }$ הוא חסר ריבועים בעוד ש- $latex { 3\cdot2\cdot2=12 }$ לא. עבור מספר טבעי $latex {n = p_1 \dotsm p_r }$ חסר ריבועים פונקציית מביוס $latex { \mu(n) }$ מוגדרת כ- $latex { (-1)^r }$ בעוד שעבור מספר שאיננו חסר-ריבועים הפונקציה מוגדרת כאפס. מתברר שלפונקציה זו יש תכונה מאוד חשובה לשיטות נפה.
משפט.
$latex \sum_{d|n} \mu(d) = \begin{cases} 1 & n=1 \\ 0 & n\ne1 \end{cases} $
שימו לב כי ברישום זה $latex { \sum_{d|n} \mu(d) }$ פירושו סכום הערכים $latex { \mu(d) }$ כאשר $latex { d }$ "רץ" על כל המחלקים של $latex { n }$.
דוגמא. $latex { \sum_{d|6} \mu(d) = \mu(1) + \mu(2) + \mu(3) + \mu(6) = 1 + (-1) + (-1) + 1 = 0 }$
נסמן: $latex { f(n) = \sum_{d|n} \mu(d) }$ אזי על פי המשפט נקבל כי \[ f(n) = \left\{ \begin{array}{l l} 1 & \quad n=1\\ 0 & \quad n\not=1 \end{array} \right.\]
מדוע זה חשוב? משום שאנו יכולים להחליף את $latex { n }$ בסכום הזה במחלק המשותף המקסימלי של $latex { n }$ ו-$latex { m }$ , מספר שאנו מסמנים אותו ב-$latex { (m,n) }$ . כשעושים זאת מקבלים \[ f((m,n)) = \left\{ \begin{array}{l l} 1 & \quad (m,n)=1\\ 0 & \quad (m,n)\not=1 \end{array} \right.\]
כלומר הפונקציה תיתן 1 כל אימת ש-$latex { (m,n)=1 }$ (שפירושו ש -$latex { n }$ ו-$latex { m }$ זרים) ואפס אחרת. אם כעת נסמן $latex {n =2\cdot3 \dotsm p_r }$ אזי $latex { f((m,2\cdot3 \dotsm p_r))}$ יתן 1 כל אימת ש-$latex { (m,2\cdot3 \dotsm p_r)=1}$ כלומר כאשר כל המחלקים הראשוניים של $latex { m } $ גדולים מ-$latex { p_r} $. כלומר הסכום $latex { \sum_{m \leq x}f((m,2\cdot3 \dotsm p_r))}$ סופר את הטבעיים עד $latex { x} $ שכל המחלקים הראשוניים שלהם גדולים מ-$latex { p_r} $. הנקודה המעניינת היא שגם קל יחסית להעריך את הסכום האחרון. לכך לא ניכנס כאן. מכאן אפשר ללמוד כל מיני שיטות להערכת הסכום האחרון. אחת מהן היא השיטה של חתן פרס פילדס ופרס וולף הנורבגי אטלה סלברג, מגדולי המתמטיקאים של המאה ועשרים (1917-2007). את השיטה הקרויה על שמו, נפת סלברג, גילה סלברג עוד בשנות החמישים של המאה ה-20. כזכור השערת התאומים הראשוניים גורסת כי יש אינסוף זוגות של ראשוניים שהמרחק ביניהם הוא 2.
ב-1985 הוכיחו גולדסטון, יילדרים ופינץ באמצעות נפת סלברג כי קיימים אינסוף זוגות של ראשוניים $latex { p_n} $ ו-$latex { p_{n+1}} $ כך שהמרחק ביניהם קטן מ- $latex { \log p_n} $. באביב שעבר הצליח ז'אנג, מתמטיקאי סיני עלום שם, לשפר את תוצאה זו לכדי 70,000,000! בסוף שנה שעברה, מיינהארד, פוסטדוקטורנט בריטי, הצליח בטכניקה שונה מזו של ז'אנג להקטין את המספר ל-600. כיום, עובדת קבוצה של מתמטיקאים בניסיון להקטין מספר זה דרך כל מיני שיפורים בחישובים. בדרך זו הצליחו לשפר את התוצאה ל-246!
עובדה מוזרה עם שלוש הוכחות
רון אהרוני
זהו פרק חותם לסדרה של שלושה מאמרים על שברים עשרוניים אינסופיים, והוא הקצר בין השלושה. אני רוצה לספר בו על מסקנה מאוד מוזרה ממה שלמדנו.
משפט 1 לכל מספר טבעי יש כפולה מן הצורה $latex {999\ldots 9000\ldots 0}$.
לא מפתיע?
אנו ניתן לעובדה הזאת שלוש הוכחות. אבל לפני שנעשה זאת - בואו נמצה מן הטענה הזאת את העיקר:
משפט 2 לכל מספר טבעי זר ל-$latex {10}$ יש כפולה מן הצורה $latex {999\ldots 9}$.
השקילות בין שני המשפטים קלה. נראה כיוון אחד: נניח שמשפט 2 נכון. בהינתן מספר $latex {n}$ כלשהו. יהא $latex {m}$ המספר $latex {n}$ מחולק בכל החזקות של $latex {2}$ ו-$latex {5}$ שמופיעות ב-$latex {n}$. אזי $latex {m}$ זר ל-$latex {10}$ ולכן על פי 2 יש לו כפולה ששווה ל-$latex {999\ldots 9}$. כפל בחזקות גדולות מספיק של $latex {2}$ ו-$latex {5}$ ייתן מספר מהצורה $latex {999\ldots 9000\ldots 0}$ שהוא כפולה של $latex {n}$.
הכיוון השני אינו יותר קשה - נסו את כוחכם.
1. הוכחה ראשונה למשפט 2 - פיתוח עשרוני
יהא $latex {n}$ מספר זר ל-$latex {10}$. מכיוון ש-$latex {\frac{1}{n}}$ הוא מספר רציונלי, על פי מה שלמדנו, השבר העשרוני המבטא אותו הוא מחזורי. למשל, $latex {\frac{1}{7}=0.\overline{142857}}$, שפירושו שהסדרה $latex {142857}$ חוזרת שוב ושוב, עד אינסוף.
למדנו איך לחזור מן הייצוג העשרוני לייצוג רציונלי: $latex {0.\overline{142857}= \frac{0.\overline{142857}}{0.\overline{999999}}}$, כי המכנה בשבר הזה הוא בעצם $latex {1}$. והשבר הזה הוא (גם זאת למדנו מדוע) $latex {\frac{142857}{999999}}$. אם כן:
$latex \displaystyle \frac{1}{7}=\frac{142857}{999999}$
שמשמעו ש-$latex {999999}$ הוא כפולה של $latex {7}$.
2. הוכחה שנייה למשפט 1 - עקרון שובך היונים, לגבי שאריות
נסתכל במספרים $latex {9,~99,~999~,\ldots 999\ldots9}$, כשהאחרון הוא בעל $latex {n}$ תשיעיות. אם אחד מהם משאיר שארית $latex {0}$ בחלוקה ב-$latex {n}$, סיימנו. אם לא, מכיוון שיש $latex {n-1}$ שאריות אפשריות, ובסדרה יש $latex {n}$ מספרים, שניים מהם משאירים אותה שארית בחלוקה ב-$latex {n}$. זהו "עקרון שובך היונים" המפורסם - אם מכניסים $latex {n}$ עצמים ל-$latex {n-1}$ תאים (סוגים) אז שניים מהם ייכנסו לאותו תא (יהיו מאותו סוג).
הפרשם של שני המספרים האלה מתחלק ב-$latex {n}$, כפי ש-$latex {93-23}$ מתחלק ב-$latex {10}$ משום של-$latex {93}$ ול-$latex {23}$ אותה שארית בחילוק ב-$latex {10}$. וכמובן ההפרש הוא בעל הצורה המבוקשת.
3. הוכחה למשפט 2 - שאריות עם מכפלה
יהא $latex {n}$ מספר זר ל-$latex {10}$. נסתכל בקבוצה $latex {\Phi}$ של המספרים הזרים ל-$latex {n}$ וקטנים ממנו. על פי ההנחה, $latex {10}$ זר ל-$latex {n}$, אם כן הוא אחד מאיברי $latex {\Phi}$.
נסתכל ב-$latex {\Phi}$ עם פעולת הכפל, כשהתוצאה נלקחת מודולו $latex {n}$, כלומר
$latex \displaystyle k \cdot \ell=k\ell(mod~ n)$
קל להיווכח בשתי עובדות:
- אם $latex {k,\ell \in \Phi}$ אז $latex {k\ell \in \Phi}$.
- אם $latex {a,b,c \in \Phi}$ ו-$latex {a\cdot b=a\cdot c}$ אז $latex {b=c}$. (הסיבה: $latex {a\cdot ((b-c)(mod~n))=0(mod~ n)}$, ומכיוון ש-$latex {a}$ זר ל-$latex {n}$ זה מחייב ש-$latex {b-c=0(mod~ n)}$, שפירושו ש-$latex {b=c}$.)
נסתכל עכשיו בחזקות של $latex {10}$ לגבי פעולת הכפל מודולו $latex {n}$. שוב, לפי עקרון שובך היונים, קיימים $latex {0<p<q \le n}$ שעבורם $latex {10^p=10^q}$. נכתוב זאת
$latex \displaystyle 10^p\cdot (10^{q-p})=10^p$
לפי ההבחנה השנייה לעיל, משמעות הדבר היא ש-$latex {10^{q-p}\equiv 1(mod~n)}$. אם נסמן את $latex {q-p}$ ב-$latex {m}$, משמעות הדבר היא ש-$latex {n}$ מחלק את $latex {999\ldots 9}$, מספר שבו $latex {m}$ תשיעיות.
למשפט 2 יש מסקנה מעניינת. על פיו אם $latex {n}$ זר ל-$latex {10}$ אז קיים מספר $latex {p}$ ש-$latex {n\times p=999\ldots 9}$, נאמר $latex {m}$ תשיעיות. על ידי הוספת אפסים לפניו, אם צריך, אפשר לכתוב את $latex {p}$ בייצוג העשרוני שלו כמספר עם $latex {m}$ ספרות, נאמר
$latex \displaystyle p=a_1a_2 \ldots a_m$
ואז, בהעברת אגפים,
$latex \displaystyle \frac{1}{n}=\frac{p}{999\ldots 9}=\frac{p=a_1a_2 \ldots a_m}{999\ldots 9}$
משמעות הדבר היא שכאשר מפתחים את $latex {\frac{1}{n}}$ לשבר עשרוני על ידי חילוק, המזור שלו מתחיל כבר מן האיבר הראשון.
יש להבין שלא כל שבר עשרוני הוא כזה. הנה דוגמה לשבר עשרוני שאינו כזה: $latex {0.000232323…}$. המחזור כאן מתחיל לא מן הספרה הראשונה אחרי הנקודה. מה שהראינו הוא שמספר כזה אינו יכול להיות מהצורה $latex {\frac{1}{n}}$ עבור $latex {n}$ זר ל-$latex {100}$. ל-$latex {n}$ כזה יכולה (למשל) להיות הצורה $latex {0.00023000230002300023…}$, אבל לא $latex {0.000232323…}$. מעניין, לא?
חידה לגדולים
רון אהרוני
חידות לילדים
קוונט - תרגום : אלכס קמרסקי
שאלה 1
על שולחן עומדות בשורה שלוש כוסות ריקות ואחריהן שלוש כוסות עם חלב. צריך לסדר את הכוסות כך שלא יהיו שתי כוסות עם חלב או שתי כוסות ריקות שבאות אחת אחרי השניה. בשביל זה מותר להשתמש רק בכוס אחד. איך אפשר לעשות את זה?
שאלה 2
שימו במקום כוכביות מספרים בפעולת כפל:
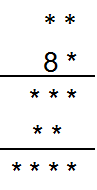
שאלה 3
אם משה ירצה לקנות סוכריה אחת, אז יישאר לו שקל אחד, ואם ירצה לקנות שתי סוכריות (מאותו סוג), אז יהיה חסר לו שקל. כמה כסף יש למשה?
שאלה 4
כיצד יש להניח 3 מטבעות, כך שכל אחד מהם ישיק ל-2 האחרים? 4 מטבעות, כך שכל אחד מהם ישיק ל-3 האחרים? 5 מטבעות, כך שכל אחד מהם ישיק ל-4 האחרים?