נטגר גליון 5
דבר העורך
רון אהרוני
ברוכים הבאים בשערי הגיליון החמישי של "נטגר".
מתמטיקאי החודש הוא דמות מרתקת (יש אומרים - יותר מדי מרתקת), מתמטיקאי ניסויי (כן, יש דבר כזה) בשם יסולא פז, שהצטרף לטכניון לא מזמן. בגיליון זה יובא ראיון איתו, שנעשה בידי מי שהיא עצמה כוח חדש במערכת - הכתבת אנה ליזהטוב. אנו מקווים שהיא תמשיך לתאר את עלילותיו של יסולא בגיליונות הבאים. ד"ר פז עצמו הבטיח לכתוב מאמרים בעצמו לגיליונות הקרובים, ולפי היכרותנו איתו את אשר הוא מבטיח הוא מקיים.
יש לנו גם מאמר מעניין של כתב ותיק יותר, אליהו לוי, על קשר נחמד בין הסתברות לגיאומטריה. קשר מפורסם כזה הוא ה"מחט של בופון" $latex {(George ~Buffon,~~1707 - 1788)}$ $latex {-}$ שיטה הסתברותית להערכת המספר $latex {\pi}$. במאמר מקושרת תגליתו של בופון למשפט על צורות מישוריות שבכל כיוון במישור יש להן אותו רוחב.
אמיר יהודיוף מן הפקולטה למתמטיקה כתב מאמר על אחת הבעיות הבסיסיות ביותר בתיאוריה של מדעי המחשב - חיפוש בינארי. אם תהיתם איך אפשר לזהות אישיות או עצם על פי $latex {21}$ שאלות של "כן" ו"לא", או איך גוגל מוצאים כל כך מהר את מה שאתם מחפשים - זוהי הזדמנות להבין.
במדור "השערת החודש" תמצאו מאמר על תופעה שהתגלתה כבר בידי אוילר - שיש פולינומים עם רצף ארוך מאוד של ערכים ראשוניים. כלומר יש רצף ארוך של הצבות, החל מ-$latex {0}$, שכל אחת מן ההצבות נותנת לפולינום ערך ראשוני. (אתם מוזמנים להוכיח שלא ייתכן רצף אינסופי כזה). וכמובן - מוזכרת השערה שנוגעת לתופעה הזאת, שאומרת שזוהי תופעה נדירה.
במדור החידות לגדולים - שלוש חידות, שאחת מהן היא חידה גיאומטרית מפורסמת, שייתכן שרבים מכירים. אבל מי שלא מכיר, כדאי מאוד שינסה את כוחו. זהו פתח לתחום גיאומטרי שלם.
בברכת הנאה,
רון אהרוני, העורך.
פולינום בעל ערכים ראשוניים
יוסי כהן
בספר בתורת המספרים של טום אפוסטול (Apostol) מסתתרת שאלה שנראית תמימה:
מצא את השלם הקטן ביותר $latex { x \ge 0}$ כך ש-$latex { f(x) = x^2 + x +41 }$ פריק.
נזכיר שמספר טבעי נקרא "פריק" אם הוא מכפלת מספרים קטנים ממנו (כלומר – "פריק" פירושו "לא ראשוני").
בבדיקה מגלים שפולינום זה מקבל ערכים ראשוניים עבור כל $latex { x=1,2,\dots,39 }$ , ורק בעבור
$latex { x=40}$ מתקבל ערך פריק. זה לא מפתיע שבערך $latex { x=40}$ מתקבל ערך פריק שהרי לכל פולינום מהצורה $latex { f(x) = x^2 + x +A }$ מקבלים כי $latex { f(A-1) = A^2 }$. מה שמפתיע הוא שכל הערכים לפני הם ראשוניים. האם אתם מכירים עוד פולינומים כאלה מהצורה $latex { f(x) = x^2 + x +A }$ שנותנים ערכים ראשוניים לכל המספרים הטבעיים הקטנים מ- $latex { A-1 }$ ?
ברור ש- $latex { f(x) = x^2 + x +2 }$ מקיים זאת, וגם הצבה של $latex { 3, 5, 11, 17 }$ במקום $latex { A }$ נותנת אותה תכונה. האם יש ערכים נוספים של $latex { A }$ שעבורם הדבר נכון? ואם לא מה מיוחד בערכי $latex { A }$ הללו?
במאמר הזה אני רוצה לספר, בלי הוכחה, על תשובה מפתיעה שניתנה עוד לפני כמאה שנה: יש רק מספר סופי של ערכי $latex { A }$ שעבורם הדבר נכון. התכונה נכונה רק כאשר $latex {A = \frac{d+1}{4}}$, עבור $latex { d = 7,11,19,43,67,163 }$.
לא נסביר את רעיון ההוכחה המקורי. נביא רעיון הוכחה אלמנטרי יותר שעושה שימוש במושג שאריות ריבועיות מודולו מספר ראשוני $latex { p }$. כדי להסביר מושג זה נבהיר לדוגמה כי השאריות הריבועיות השונות מאפס מודולו $latex { 5 }$ הן $latex { 1 }$ ו-$latex { 4 }$, משום ש:
$latex { 1^2 = 1 }$
$latex { 2^2 = 4 }$
$latex { 3^2 = 4 }$
$latex { 4^2 = 1 }$
שימו לב שמספיק היה לקחת את החזקות הריבועיות של $latex { 1 }$ ו- $latex { 2 }$. יש לכך סיבה: בשאריות מ-$latex { 5 }$, מתקיים $latex { 3=-2 }$ ו-$latex { 4=-1 }$. משום כך$latex { 3^2 = (-2)^2 = 2^2 }$ (בשאריות מ-$latex { 5 }$). מאותה סיבה מספיק לקחת את כל החזקות הריבועיות של $latex { 1,2, \dots \frac{p-1}{2} }$ מודולו $latex { p }$. כלומר מספר השאריות הריבועיות הוא לכל היותר $latex { p/2 }$, ולמעשה הוא בדיוק $latex { p/2 }$, משום שכל שארית מתקבלת בדיוק פעמיים, משום שלמשוואה ריבועית מן הסוג $latex { x^2 = k }$ מודולו $latex { p }$ יש לכל היותר שני פתרונות (כמו למשוואות ריבועיות מעל הממשיים)
נסתכל כעת על $latex { p=7 }$. הריבועים הם
$latex { 1^2 = 1 }$
$latex { 2^2 = 4 }$
$latex { 3^2 = 2 }$
כלומר הריבועים מודולו $latex { 7 }$ הם: $latex { 1,2,4 }$.
שימו לב ש-$latex { 2 }$ הוא גם ריבוע מודולו $latex { 7 }$ והוא עצמו ראשוני. אומרים אז ש- $latex { 2 }$ הוא ריבוע ראשוני מודולו $latex { 7 }$.
באופן דומה, הריבועים מודולו $latex { 11 }$ הם $latex { 1,3,4,5,9 }$. שימו לב כי $latex { 3 }$ ו-$latex { 5 }$ הם ריבועים ראשוניים מודולו $latex { 11 }$. אפשר להראות שלכל ראשוני $latex { p }$ קיימים "הרבה" ראשוניים שהם ריבועים מודולו $latex { p }$. שאלה מעניינת בתורת המספרים היא: בהינתן ראשוני $latex { p }$, מהו הריבוע הראשוני הקטן ביותר $latex { \ell(p) }$?
הבעיה הזו פתוחה כבר מראשית המאה הקודמת. ההשערה היא שהמספר מאוד קטן. מה שיודעים בשלב זה להוכיח הוא שעבור $latex { p }$ מספיק גדול סדר הגודל של $latex { \ell(p) }$ הוא $latex { \sqrt{p}}$. אכן, הרבה פחות מן החסם הפשוט $latex { p/2 }$.
כעת, אנחנו יכולים לחבר את הבעיה הזו עם הבעיה שפתחנו בה. מתברר שאפשר להוכיח את המשפט הבא:
$latex { E_d(x) = x^2 + x + \frac{d+1}{4} }$ הוא ראשוני לכל $latex { d = 0,1, \dots \frac{d+1}{4}-2 }$ אם ורק אם $latex { d }$ ראשוני ומתקיים $latex { \ell(d) = \frac{d+1}{4} }$.
כיוון שיודעים להוכיח שעבור $latex { d }$ ראשוני סדר הגודל של $latex { \ell(d) }$ הוא $latex { \sqrt{d}}$ , של-p גדול הוא הרבה יותר קטן מאשר $latex { (p+1)/4 }$, ברור כי יש מספר סופי של פולינומים כאלה. למעשה, נכון דבר מפתיע: אין עוד פולינומים כאלה, נוסף לאלה שצויינו לעיל!
Apostol, Tom M. Introduction to Analytic Number Theory (1976). New York-Heidelberg-Berlin, Springer-Verlag
חיפוש בינארי
אמיר יהודיוף
הקדמה:
אתם בוודאי מכירים את המשחק ״21 שאלות״. מישהו בוחר דמות, או מקום, או אירוע, והמשתתפים אמורים לגלות את מה שחשב עליו בעזרת 21 שאלות. הכלל הוא שהתשובות צריכות להיות רק ״כן״ או ״לא״. אסור, למשל, לשאול ״על איזו דמות חשבת?״.
המוזר הוא שזו אינה משימה בלתי אפשרית. למעשה בדרך כלל מצליחים. איך זה יכול להיות? יש כל כך הרבה דמויות בעולם, זמרים וציירים, סופרים ושחקנים, ובכל זאת אפשר לגלות את הדמות, כשכל המידע הניתן הוא ״כן״ או ״לא״. מהו הסוד?
הסוד טמון בשיטה שבעזרתה אנחנו מצליחים לבטא מספר ענקי כמו מיליון בעזרת שבע ספרות בלבד. וברעיון שעליו דיברנו כשסיפרנו על סדרות גיאומטריות: שסדרות גיאומטריות גדלות מהר מאוד אם המנה שלהן גדולה מ־1, וקטנות מהר מאוד אם המנה קטנה מ־1. הוא נקרא ״חיפוש בינארי״.
חיפוש בינארי לא רק עוזר לשחק משחקים, אלא גם בפתרון בעיות בחיים. דמיינו, לדוגמא, מצב בו ישנה רשימה של $latex {4}$ פעילויות חברתיות אפשריות, נאמר: אוכל, סרט, ים ובריכה. ושאתם מעוניינים לתאם עם חבריכם את הפעילות למחר. כמה שאלות כן-לא נדרשות על מנת לדעת מהי הפעילות העדיפה עליהם? באופן דומה, דמיינו שאתם רוצים לברר מספר טלפון של אדם שזה אתה פגשתם. כמה שאלות כן-לא דרושות על מנת להשיג זאת?
הצעד הראשון שנעשה יהיה להגדיר את הבעיה באופן מתמטי. הגדרה זו תאפשר לנו לדון בבבעיה באופן מדויק. בהמשך נשתמש בטיעונים לוגיים מסוגים שונים כדי לספק תשובה מדוייקת לשאלה שמעניינת אותנו. מצד אחד נראה שכדי ללמוד על חברינו, השיחות עמהם לא יכולות להיות קצרות מדי. מצד שני נלמד כיצד לשאול שאלות באופן שבו המידע שכל תשובה מוסיפה הוא משמעותי. בעיות דומות נחקרות גם היום ברחבי העולם, עם מוטיבציות שקשורות לחישוב, תקשורת, ומדע בכלל.
הגדרות:
נתחיל בהגדרת את חוקי המשחק, ובתיאור מופשט שלו. את רשימת האפשרויות נחליף במספרים
$latex \displaystyle .1,2,3,\ldots,n$
כל מספר ברשימה מתאים לאחת הדמויות האפשריות, או לאחת הפעילויות האפשריות, או לאחד ממספרי הטלפון האפשריים. נניח שלחברנו ידוע מספר $latex {X}$ מתוך רשימת המספרים, ואנו לא יודעים מהו $latex {X}$. כמו כן נניח כי אנו יכולים לשאול את חברנו כל שאלת כן-לא העולה על רוחנו. למשל, "האם $latex {X}$ הוא לפחות 12?״. השאלה שתנחה אותנו היא:
מהו המספר הקטן ביותר $latex {Q}$ של שאלות כן-לא הדרושות כדי לדעת מהו $latex {X}$?
שאלת מחקר זו מופיעה באופן טבעי בהקשרים שונים, והתשובה לה מעניינת הן מבחינה תאורטית והן מבחינה מעשית.
המשפט המתמטי הבא מתאר את התשובה לשאלה, ונוכיחו בהמשך.
משפט: לכל מספר $latex {n}$ טבעי, מתקיים $latex {.2^{Q-1} < n \leq 2^{Q}}$
כדי להבין את המשפט טוב יותר, נתבונן בגרף 1 שמתאר את הקשר בין מספר השאלות $latex {Q}$ ומספר האפשרויות $latex {n}$ עבור ערכי $latex {n}$ בין $latex {1}$ ל $latex {200}$.
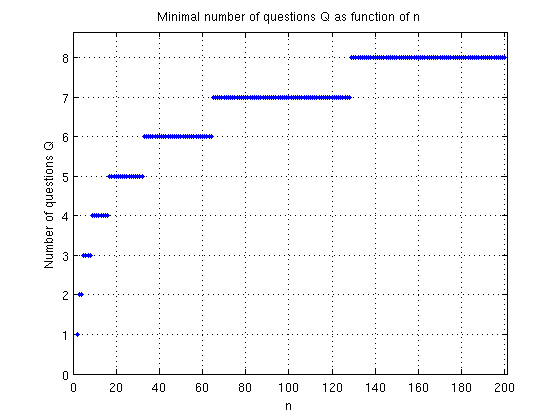
גרף $latex {:1}$ קשר בין מספר שאלות מינימלי למספר האפשרויות
הגרף מראה למשל שאם ישנן 20 אפשרויות $latex {(n=20)}$ אז נזדקק ל $latex {5}$ שאלות, ואם $latex {n=200}$ אז נזדקק ל $latex {8}$ שאלות. כמו כן, ניתן לראות שהתלות בין $latex {Q}$ ל $latex {n}$ אינה לינארית, כלומר אינה מתוארת על ידי קו ישר. סוג הקשר בין $latex {Q}$ ל $latex {n}$ נקרא קשר לוגריתמי. המשפט גם מתאר כמה שאלות כן-לא דרושות על מנת לגלות מספר טלפון בן שבע ספרות: דרושות בסך הכל עשרים וארבע שאלות! מהן השאלות? זאת נראה בהמשך (באופן מופשט).
הוכחת המשפט:
להוכחה שני חלקים שונים. אי השיוויון השמאלי משמעותו מציאת רשימת שאלות קצרה שמבטיחה שלאחר שנשאל את כולה נדע את המידע החבוי $latex {X}$. אי השיוויון הימני משמעותו שאם רשימת השאלות קצרה מדי אז בסיומה עדיין תהיה חוסר וודאות לגבי הערך המדויק של $latex {X}$.
אי השיוויון הימני: מעט שאלות לא מספיקות
נתחיל בלהוכיח את הטענה הבאה: לכל $latex {L \geq 0}$ טבעי, ולכל רשימת שאלות כן-לא באורך $latex {L}$, ישנה קבוצה בגודל לפחות $latex {n/2^L}$ של מספרים בין $latex {1}$ ל $latex {n}$ שרשימת השאלות לא מבדילה בניהם (כלומר כך שהתשובות לכל $latex {L}$ השאלות הן זהות לכל המספרים בקבוצה).
הוכחת הטענה: עבור $latex {L=0}$, טענה זו כמובן נכונה כי לא נשאלה אף שאלה ו $latex {2^0=1}$. עבור $latex {L=1}$, קבוצת האפשרויות מתחלקת לשני חלקים בהתאם לתשובה לשאלה שנשאלה. אחד משני החלקים חייב להיות לכן בגודל לפחות חצי, כלומר בגודל לפחות $latex {n/2}$. נבחר חלק זה. עבור $latex {L=2}$, נתבונן בחלק שנבחר לאחר השאלה הראשונה וגודלו לפחות $latex {n/2}$. נשים לב שלאחת התשובות לשאלה השניה יש תשובה שלה מתאימים לפחות $latex {\frac{1}{2} \cdot n/2 = n/2^2}$ אפשרויות, וכן הלאה.
מסקנה מהטענה: אם $latex {2^L < n}$ אז בכל רשימה של $latex {L}$ שאלות ישנם לפחות שני מספרים שונים $latex {(n/2^L > 1)}$ שהשאלות לא מבדילות בניהם. אם כך, בכמות כזו של שאלות לא נצליח באופן וודאי לגלות את ערך $latex {X}$. לכן, $latex {2^Q \geq n}$.
אי השיוויון השמאלי: בחירת השאלות
עלינו למצוא סדרת שאלות מתאימה. הרעיון הוא להשתמש בחיפוש בינארי, המתבצע כך: ישנם $latex {n}$ מספרים. נגדיר $latex {M}$ להיות הטבעי הקטן ביותר כך ש $latex {n \leq 2^M}$. מינימליות $latex {M}$ גוררת ש $latex {2^{M-1} < n}$. נסביר כיצד לגלות את $latex {X}$ בעזרת $latex {M}$ שאלות כן-לא. בכך נסיים ההוכחה.
השאלה הראשונה שנשאל היא ״האם $latex {X<(1/2) \cdot 2^{M}}$?״. אם התשובה היא כן, נמשיך ונשאל ״האם $latex {X<(1/4) \cdot 2^{M}}$?״ ואחרת נשאל ״האם $latex {X<(3/4) \cdot 2^M}$?״. וכן הלאה. ניתן לראות שלאחר השאלה הראשונה כמות האפשרויות ל $latex {X}$ היא לכל היותר $latex {\frac{1}{2} \cdot 2^M = 2^{M-1}}$. לאחר השאלה השניה הכמות קטנה ל $latex {2^{M-2}}$. באופן כללי, לאחר $latex {L}$ שאלות כמות האפשרויות תהיה $latex {2^{M-L}}$. לאחר $latex {M}$ שאלות כמות האפשרויות היא $latex {2^{M-M} = 1}$, כלומר נדע את $latex {X}$ בוודאות.
ייצוג בינארי:
לאחר שהבנו דבר מה לגבי שאילת שאלות, נדבר בקצרה על שפה או ייצוג של מילים, מספרים ומושגים באופן בינארי.
ייצוג עשרוני של מספר הוא דבר מוכר לכולם. לכל כפולה של עשר יש ספרה משלה: ספרת אחדות $latex {10^0 = 1}$, ספרת עשרות $latex {10^1 = 10}$, ספרת מאות $latex {10^2 = 100}$… והסימון $latex {106}$ מייצג את המספר $latex {1 \times 100 + 0 \times 10 + 6 \times 1}$.
באופן דומה, ניתן לייצג מספר בינארית, בבסיס שתיים במקום בבסיס עשר. במקום עשר ספרות, ישנן רק שתיים: $latex {0,1}$. בייצוג זה ישנה ספרה שמתאימה ל $latex {2^0 = 1}$, ספרה שמתאימה ל $latex {2^1 = 2}$, ספרה שמתאימה ל $latex {2^2 = 4}$… והסימון $latex {101}$ מייצג למשל את $latex {1 \times 4 + 0 \times 2 + 1 \times 1}$, כלומר את המספר חמש.
מה הקשר לשאלות כן-לא? ובכן ניתן לפרש את הספרה $latex {1}$ כ״לא״ ואת הספרה $latex {0}$ כ״כן״. עם פרשנות זו, ייצוג בינארי מתאים בדיוק לתשובות המתקבלות בחיפוש הבינארי שדיברנו עליו. למשל אם $latex {n=8}$ ו $latex {X = 5}$, נשאל ״האם $latex {X < 4}$?״ והתשובה תהיה ״לא״. תשובה זו מתאימה ל $latex {1}$ השמאלי בייצוג הבינארי של חמש. נמשיך ונשאל ״האם $latex {X < 6}$?״ והתשובה ״כן״ מתאימה ל $latex {0}$. לסיום, התשובה ל ״האם $latex {X<5}$?״ היא ״לא״ ומתאימה ל $latex {1}$ הימני.
באופן מעט יותר כללי, תיארנו קשר בין הייצוג הבינארי של מספר לבין תשובות לשאלות כן-לא לגביו. אם למספר יש $latex {21}$ ספרות בייצוג הבינארי, אז ניתן למצוא אותו בפשטות על ידי שאילת $latex {21}$ שאלות: ״האם הספרה הראשונה היא $latex {0}$?״, ״האם הספרה השניה היא $latex {0}$?״, וכן הלאה. יש קשר ישיר בין הייצוג הבינארי של מספר ובין התשובות לרשימת השאלות הזו. מכך נסיק שבאמצעות $latex {21}$ שאלות אפשר לתאר $latex {2^{21} = 2,097,152}$ דברים! לשם השוואה, מספר המילים במילון בשפה העברית הוא קטן בהרבה, ומוערך להיות פחות מ $latex {100,000}$.
נסיים במחשבה על כפות ידינו. בדרך כלל משתמשים באצבעות כדי לייצג מספרים בין אחד לעשר. עכשיו כשלמדנו מעט, אנחנו מבינים שעם חמש האצבעות של כף יד אחת ניתן לייצג בפשטות $latex {2^5 = 32}$ מספרים. תנסו. כמה אפשר עם כל עשר האצבעות?
ממוצע משוקלל, הסתברות, תוחלת ועקומים בעלי רוחב קבוע
אליהו לוי
(לפי הרוזן בופון והרצאה של פרופ' גיל קלעי)
הקדמה: ממוצע משוקלל, תוחלת
כולנו יודעים מהו ממוצע (חשבוני): נתונים $latex {n}$ מספרים $latex {a_1,a_2,\ldots,a_n}$, אז הממוצע שלהם יהיה
$latex \displaystyle \mu:=\frac1n(a_1+a_2+\ldots a_n).$
אבל אנו יכולים לקחת כל $latex {a_i}$ כמה פעמים: את $latex {a_1}$, $latex {k_1}$ פעמים, את $latex {a_2}$, $latex {k_2}$ פעמים, וכן הלאה, כאשר את מספר הפעמים הכולל $latex {k_1+k_2+\ldots+k_n}$ נסמן ב-$latex {N}$. אז, כמו שנוכחים מייד, הממוצע יהיה:
$latex \displaystyle \mu:=\frac{k_1}N a_1+\frac{k_2}N a_2+\ldots+\frac{k_n}N a_n.$
כלומר ה-$latex {a_i}$-ים מוכפלים במקדמים - משקלות - $latex {\frac{k_i}N}$, ושימו לב שהמשקלות הם מספרים (במקרה זה, שברים) השייכים לקטע $latex {[0,1]}$, וסכומם הוא
$latex \displaystyle \frac{k_1}N+\frac{k_2}N+\ldots+\frac{k_n}N=1.$
זה מביא אותנו לממוצע משוקלל. יש לנו $latex {n}$ משקלות, שהם $latex {n}$ מספרים אישליליים (לאו דווקא רציונליים) $latex {\omega_1,\omega_2,\ldots,\omega_n}$ שסכומם $latex {1}$, והממוצע המשוקלל לגבי משקלות אלה יוגדר כ:
$latex \displaystyle \mu:=\omega_1 a_1+\omega_2 a_2+\ldots+\omega_n a_n. \ \ \ \ \ (1)$
לזה יש פירוש הסתברותי: נניח שיש לנו $latex {n}$ אפשרויות, שאנו ממספרים אותן ב $latex {1,2,\ldots,n}$, כך שלאפשרות $latex {1}$ יש הסתברות $latex {\omega_1}$ , לאפשרות $latex {2}$ יש הסתברות $latex {\omega_2}$ , וכן הלאה (וכאן חשוב מאוד שהינחנו שסכום ה$latex {\omega}$'ים הוא $latex {1}$!). נניח שעשינו מדידה, שבאפשרות ה-$latex {i}$ תיתן תוצאה $latex {a_i}$, עבור $latex {i=1,\ldots,n}$. כלומר: אם נעשה את המדידה, תתגשם אחת התוצאות $latex {i}$, ואז תוצאת המדידה תהיה $latex {a_i}$. אז לממוצע המשוקלל (1) קוראים התוחלת של תוצאת המדידה.$latex {^1}$
דוגמה: נזרוק קוביה הוגנת, וה"מדידה" $latex {a_i}$ סופרת את המספר שיצא. כאן מספר האפשרויות $latex {n}$ הוא $latex {6}$, ואם הקוביה אכן הוגנת אז כל ההסתברויות $latex {\omega_i}$ , $latex {i=1,\ldots,6}$ שוות ל $latex {1/6}$, והתוחלת היא $latex {\frac16(1+2+3+4+5+6)=3.5}$. (כאן התוחלת בכלל אינה תוצאה שיכולה להתקבל!).
הערה 1: מדוע קוראים לזה "תוחלת"? סיבה מרכזית לכך שרואים ביטוי זה (1) כ"תוחלת" - הערך שהכי ראוי לצפות לו - הוא עובדה שנקראת משפט המספרים הגדולים. היא אומרת שאם נסכם (או נמצע) הרבה מדידות אקראיות בלתי-תלויות אז הסכום, (או הממוצע) של המדידות, שתמיד התוחלת שלו היא סכום (או ממוצע) התוחלות, ייתן בכלל, כמעט בוודאות, תוצאה קרובה מאוד לתוחלת שלו.
דוגמא: זורקים קוביה הוגנת, ונקבע ערך $latex {1}$ למדידה אם הקוביה נפלה על $latex {1}$, וערך $latex {0}$ אחרת. אז התוחלת תהיה שווה ל-$latex {1/6}$ (מדוע?). בהתאם למשפט המספרים הגדולים, אם נזרוק קוביה הוגנת, באופן בלתי תלוי, מספר גדול $latex {N}$ של פעמים, יהיה הסכום של תוצאות ה"מדידה" שלנו, השווה למספר הפעמים שיצא $latex {1}$ (מדוע?), כמעט בוודאות קרוב לתוחלת שלו, שהיא סכום התוחלות $latex {(1/6)N}$.
מהדוגמה האחרונה אנו רואים שאת ההסתברות של מאורע $latex {E}$ נוכל לתאר כתוחלת של ה"מדידה" שמוגדרת כנותנת $latex {1}$ אם $latex {E}$ קרה ו-$latex {0}$ אם $latex {E}$ לא קרה. חוק המספרים הגדולים ייתרגם אז לתכונה הבסיסית של הסתברות: שההסתברות של $latex {E}$ היא, כמעט בוודאות, קרובה מאוד לשכיחות של התקיימות $latex {E}$ בסדרת הרבה חזרות בלתי תלויות על ה"ניסוי".
מערכת "אינסופית". עד עכשיו היה לנו ממוצע משוקלל, במלים אחרות, תוחלת, של מספר סופי של תוצאות $latex {a_i}$, אבל ניתן להגדיר אותו גם כאשר יש אינסוף תוצאות - למשל סידרה אינסופית $latex {a_i,i=1,2,\ldots}$ או מערכת התלויה בפרמטר רציף כגון $latex {a(x)}$ או $latex {a(x,y)}$. אפשר לתת הגדרות מדוייקות - במקום סכום יבוא סכום טור או אינטגרל - ותמיד אפשר להיעזר בסימטריות הקיימות במערכת.
למשל, מהסימטריה נובע שהתוחלת של גובה נקודה בכדור מלא, (או רק בפני הכדור), היא גובה מרכז הכדור! (ומה בדבר נקודה על מעגל או עיגול במישור או נקודה על מעגל או עיגול במרחב?).
כאשר נדון בהמשך במערכות "אינסופיות" כאלה, נסתמך על האינטואיציה, למרות שיש דרכים סטנדרטיות לעשות הכל בדיוק מלא.
הערה 2. בכל מקרה, ברור שמתקיימים משפטים כמו: אם המדידה "קבועה", כלומר ערכה בהכרח קבוע $latex {a}$, אזי גם התוחלת היא $latex {a}$; אם שתי מדידות $latex {a_i}$ ו $latex {b_i}$ על אותו מרחב הסתברות מקיימות: בהכרח $latex {a_i\le b_i}$, אז התוחלת של $latex {a_i}$ קטנה או שווה מזו של $latex {b_i}$. מתקיים עוד: התוחלת של סכום "מדידות" היא סכום התוחלות אבל זה לא נכון לגבי מכפלות!, (נסו למצוא דוגמה נגדית) - עם זאת, זה נכון אם אחת הנכפלות היא קבוע: התוחלת של כפל "מדידה" $latex {a_i}$ בקבוע $latex {K}$ היא $latex {K}$ כפול התוחלת של $latex {a_i}$.
אורך עקומים כתוחלת, עקומים קמורים בעלי רוחב קבוע
תהי $latex {D}$ מערכת ישרים מקבילים במישור במרחקים שווים $latex {d}$. נזיז ונסובב את $latex {D}$ "באופן אקראי", ונקבל מערכות אחרות $latex {D'}$ של ישרים מקבילים, למעשה נקבל את כל המערכות האפשריות של מערכות ישרים מקבילים במישור עם מרחק $latex {d}$ ביניהם. באופן אינטואיטיבי נראה שבקבוצת כל המערכות $latex {D'}$ האלה, שנסמן אותה ב-$latex {\mathbf{D}}$, יש משמעות (מוגדרת באופן יחיד!) להסתברות שהיא אינווריאנטית לגבי הזזות וסיבובים (זה קשור לכך שבאופן הסתכלותי $latex {\mathbf{D}}$ היא חסומה - נמצאת בתחום מוגבל, כי אם נסובב ונזיז את $latex {D}$ למרחק גדול נוכל לקבל אותה $latex {D'}$ ע"י סיבוב והזזה למרחק "קרוב"). למשל ההסתברות שכיוון הישרים ב $latex {D'}$ יהיה ברביע הראשון והשלישי היא $latex {1/2}$. ההסתברות ש $latex {D'}$ יוצאת מקבילה לציר $latex {y}$ היא $latex {0}$. ההסתברות ש $latex {D'}$ עוברת דרך הראשית גם היא $latex {0}$, וכן הלאה.
כעת יהא נתון עקום או מערכת עקומים $latex {c}$, ונסמן ב $latex {\lambda(c)}$ את התוחלת של מספר נקודות החיתוך של $latex {c}$ עם מערכת המקבילים המשתנה (במלים אחרות, אקראית) $latex {D'}$. נראה כמה תכונות של $latex {\lambda(c)}$ (את ה"הוכחות", או אינטואיטיביות או לא קשות, נשאיר לקוראים/ות).
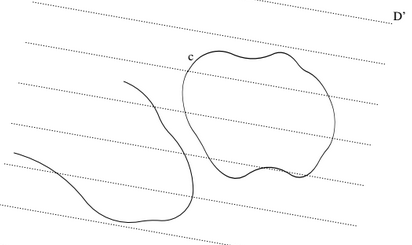
תכונה 1. אם מזיזים או מסובבים את $latex {c}$, $latex {\lambda(c)}$ לא משתנה.
תכונה 2. אם $latex {c}$ היא נקודה אחת או קבוצה סופית של נקודות אזי $latex {\lambda(c)=0}$.
תכונה 3. אם $latex {c'}$ מכילה את $latex {c}$, אזי $latex {\lambda(c')\ge\lambda(c)}$. במילים אחרות: $latex {\lambda}$ מונוטונית עולה.
תכונה 4. עבור $latex {c_1}$ ו- $latex {c_2}$ כלשהם,
$latex \displaystyle \lambda(c_1\cup c_2)=\lambda(c_1)+\lambda(c_2)-\lambda(c_1\cap c_2),$
(כי שוויון כזה נכון לגבי מספרי נקודות החיתוך עם כל $latex {D'}$ שניקח, בידקו!)
ובמיוחד אם $latex {c_1\cap c_2}$ היא קבוצה סופית אז לפי תכונה 2. $latex {\lambda(c_1\cup c_2)=\lambda(c_1)+\lambda(c_2)}$.
תכונה 5. ניקח במיוחד $latex {c_a}$ $latex {=}$ קטע באורך $latex {a}$. לפי תכונה 1. $latex {\lambda}$ של קטע כזה תלויה רק באורכו $latex {a}$ ולא במקומו. לפי תכונה 4. $latex {\lambda(c_{a+b})=\lambda(c_a)+\lambda(c_b)}$. כלומר $latex {\lambda(c_a)}$ היא פונקציה אדיטיבית של $latex {a}$ ( $latex {a}$ משתנה כאן על המספרים האי-שליליים). לפי תכונה 3. $latex {\lambda(c_a)}$ היא פונקציה מונוטונית עולה של $latex {a}$. כידוע, פונקציה אדיטיבית ומונוטונית כזו חייבת להיות מהצורה $latex {Ka}$ כאשר $latex {K}$ קבוע. כלומר קיים קבוע $latex {K}$ כך ש $latex {\lambda}$ של קטע באורך $latex {a}$ הוא $latex {Ka}$.
תכונה 6. אם $latex {c}$ קו שבור, נוכל להרכיב אותו מקטעים ולהשתמש בתכונה 4. מקבלים שגם עבור קו שבור $latex {c}$, $latex {\lambda(c)}$ $latex {=}$ $latex {K}$ כפול אורכו של $latex {c}$.
תכונה 7. אנו רוצים, כמובן, לקבל אותה טענה כמו 6. עבור $latex {c}$ קו עקום. נניח ש $latex {c}$ לא "משתולל" - שהוא לא "פרקטלי" כמו, למשל, פתית השלג של קוך. נניח שהוא קו חלק עם, אולי, מספר סופי של פינות (אם כותבים הוכחה מדוייקת, מה שאנו לא ממש נעשה, מגדירים במדוייק מה דורשים מ-$latex {c}$). ניקח ב-$latex {c}$ סדרות של נקודות, והן יהיו קודקודי קווים שבורים $latex {c'}$ החסומים ב-$latex {c}$, וניקח סידרת $latex {c'_n}$-ים כאלה עם מרחקים בין קודקודים סמוכים ב-$latex {c'_n}$ שואפים ל-$latex {0}$ כאשר $latex {n\rightarrow\infty}$.
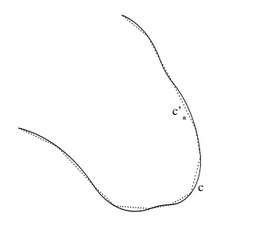
אורכי $latex {c'_n}$ שואפים לאורכו של $latex {c}$. מצד שני נראה באופן הסתכלותי שכאשר $latex {n}$ גדול צריך להיות למערכת המקבילים $latex {D'}$ "מזל מיוחד" - שהיא תצא כמעט משיקה ל-$latex {c}$ באיזשהו מקום - כדי שמספר נקודות החיתוך של $latex {D'}$ עם $latex {c'_n}$ לא יהיה שווה למספר נקודות החיתוך של $latex {D'}$ עם $latex {c}$. וגם אם קורה "מזל מיוחד" זה אז מספרי נקודות החיתוך לא שונים בהרבה זה מזה. כלומר מספרי נקודות החיתוך של $latex {c'_n}$ ו-$latex {c}$ עם $latex {D'}$ האקראי הם כמעט בוודאות שווים, ובמקרה הנדיר שהם שונים ההבדל ביניהם אינו ענקי. במקרה כזה גם התוחלות $latex {\lambda(c'_n)}$ ו $latex {\lambda(c)}$ צריכות להיות קרובות מאוד, יותר ויותר כאשר $latex {n\rightarrow\infty}$, במלים אחרות, $latex {\lambda(c'_n)\rightarrow\lambda(c)}$. ועכשיו, $latex {\lambda(c'_n)}$ $latex {=}$ $latex {K}$ כפול אורכו של $latex {c'_n}$, וכאשר $latex {n\rightarrow\infty}$, $latex {\lambda(c'_n)\rightarrow\lambda(c)}$ ואורכו של $latex {c'_n}$ שואף לאורכו של $latex {c}$, ומכאן מקבלים ש $latex {\lambda(c)}$ $latex {=}$ $latex {K}$ כפול אורכו של $latex {c}$.
הערה 3. שימו לב לעובדה הדי מפתיעה, שבתכונות 1. - 7. לא השתמשנו בכך ש $latex {D}$ היא דווקא מערכת קווים מקבילים - הן יישארו נכונות, עם אותן הוכחות, אם ניקח כ- $latex {D}$ "גלים", אפילו גלים שבורים (ראו בציור), וניקח כ $latex {\mathbf{D}}$ את כל ההזזות והסיבובים של $latex {D}$. זה בתנאי רק שיש ל $latex {D}$ מחזוריות בשני כיוונים שונים, מה שיבטיח ש $latex {\mathbf{D}}$ "חסומה" ואז יש בה הסתברות אינווריאנטית לגבי סיבובים והזזות. אלא רק שלכל $latex {D}$ יהיה קבוע $latex {K=K(D)}$ אחר. נשאיר כתרגיל לקוראים/ות לחקור את אופי התלות של $latex {K(D)}$ ב-$latex {D}$.
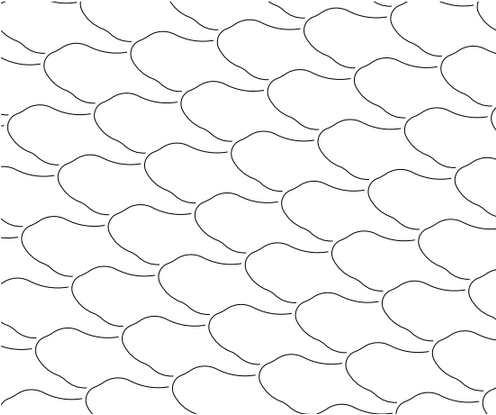
אבל נחזור ל $latex {D}$ - מערכת קווים מקבילים במרחק $latex {d}$. האם נוכל לחשב את $latex {K}$?
ניקח כ-$latex {c}$ מעגל בקוטר $latex {d}$. אז מספר נקודות החיתוך הוא תמיד $latex {2}$! לכן התוחלת שלו $latex {\lambda(c)}$ היא בוודאי $latex {2}$, וזה שווה ל $latex {K}$ כפול אורכו-הקפו של $latex {c}$, שהוא $latex {\pi d}$. מכאן $latex {K=\dfrac2{\pi d}}$.
ולבסוף קיבלנו,
משפט 1. התוחלת של מספר נקודות החיתוך של מערכת קווים מקבילים בעלי מרחק $latex {d}$ במיקום "אקראי", עם עקום או מערכת עקומים $latex {c}$, היא $latex {\dfrac2{\pi d}}$ כפול אורכו של $latex {c}$.
ומקבלים מסקנה לגבי עקומים קמורים $latex {c}$ בעלי רוחב קבוע - כלומר בעלי התכונה שהמרחק $latex {d}$ בין שני קווים מקבילים החוסמים את $latex {c}$ לא תלוי בכיוון שלהם, במילים אחרות, שאורך ההטלה של $latex {c}$ על מסך ישר לא תלוי בכיוון המסך. המעגל הוא בעל רוחב קבוע, אבל יש הרבה אחרים - ראו בציור. למעשה, בהרבה מקרים קשת עקומה קמורה שהמשיקים בקצותיה מקבילים במרחק $latex {d}$ אפשר להשלים לעקום בעל רוחב קבוע $latex {d}$, ע"י העברת מקבילים במרחק $latex {d}$ לכל המשיקים לקשת ולקיחת העקומה העוטפת שלהם.

וכעת, לכל עקום בעל רוחב קבוע $latex {d}$ יש אותה תכונה כמו המעגל, שמספר נקודות החיתוך עם $latex {D'}$ הוא תמיד $latex {2}$! מכאן וממשפט 1. נובע מייד:
משפט 2. כל עקום קמור בעל רוחב קבוע $latex {d}$ הוא בעל אותו הקף $latex {\pi d}$ כמו מעגל בקוטר $latex {d}$.
וריאציות
וריאציה 1
נחליף את $latex {D}$ בסריג במישור, למשל קבוצת הנקודות $latex {(x,y)}$ עם $latex {x}$ ו $latex {y}$ שלמים. כמו קודם, $latex {\mathbf{D}}$ היא קבוצת כל ההזזות וסיבובים האקראיים $latex {D'}$ של $latex {D}$. כ- $latex {c}$ כדאי כעת לקחת תחום, למשל מצולע מלא (מדוע?). בדיוק כמו קודם, מקבלים שהתוחלת של מספר נקודות החיתוך של $latex {c}$ עם $latex {D'}$ היא קבוע כפול שיטחו של $latex {c}$.
וריאציה 2.
במרחב, התוחלת של מספר נקודות החיתוך של מערכת מישורים מקבילים במרחק $latex {d}$ במיקום אקראי עם עקום מרחבי (או מערכת עקומים), היא קבוע כפול אורך העקום.
וריאציה 3.
במרחב, התוחלת של מספר נקודות החיתוך של הזזה-סיבוב אקראית של סריג מסויים של קווים מקבילים עם משטח (או מערכת משטחים), היא קבוע כפול שטח הפנים של המשטח.
וריאציה 4.
ובישר, התוחלת של מספר נקודות החיתוך של הזזה אקראית של קבוצת הכפולות של $latex {d}$, עם קבוצה קבועה $latex {c}$, היא קבוע כפול אורכה של $latex {c}$. הקבוע שווה ל $latex {1/d}$, כמו שרואים אם ניקח $latex {c}$ $latex {=}$ קטע באורך $latex {d}$.
מכאן שבמישור, התוחלת של מספר נקודות החיתוך של עקום קמור $latex {c}$ עם מערכות אקראית של קווים מקבילים במרחק $latex {d}$ שהם בכיוון מסויים קבוע $latex {\vec{v}}$ $latex {=}$ $latex {2}$ $latex {\times}$ התוחלת של מספר נקודות החיתוך של הזזה אקראית של קבוצת הכפולות של $latex {d}$ עם ההטלה של $latex {c}$ על "מסך" מאונך ל-$latex {\vec{v}}$ $latex {=}$ $latex {2/d}$ $latex {\times}$ האורך של ההטלה. מכאן וממשפט 1. מקבלים הכללה של משפט 2:
משפט 3. התוחלת של אורך ההטלה של עקום קמור $latex {c}$ על ישר בכיוון אקראי היא $latex {1/\pi}$ כפול הקפו של $latex {c}$.
וריאציה 5.
נעשה דבר דומה לוריאציוה 4, אבל במרחב.
התוחלת של מספר נקודות החיתוך של משטח קמור קבוע $latex {c}$ עם סריג קווים מקבילים אקראי בכיוון מסויים $latex {\vec{v}}$ $latex {=}$ $latex {2}$ $latex {\times}$ התוחלת במישור של מספר נקודות החיתוך, עם ההטלה של $latex {c}$ על "מסך" מאונך ל-$latex {\vec{v}}$, של הזזה או סיבוב של הסריג המתאים (שהוא החיתוך של הקווים המקבילים עם מישור מאונך להם), וזה שווה, לפי וריאציה $latex {1}$, לקבוע כפול השטח של ההטלה.
מכאן ומוריאציה 3. מקבלים במרחב, שהתוחלת של השטח של ההטלה של משטח קמור על מישור בכיוון אקראי, היא קבוע כפול שיטחו של $latex {c}$.
את ערך הקבוע נמצא בעזרת המקרה $latex {c}$ $latex {=}$ פני כדור ברדיוס $latex {r}$. אז שטח ההטלה הוא תמיד $latex {\pi r^2}$ ושטח הכדור הוא $latex {4\pi r^2}$. לכן הקבוע הוא $latex {1/4}$, וקיבלנו,
משפט 4. התוחלת של השטח של ההטלה של משטח קמור $latex {c}$ על מישור בכיוון אקראי, היא $latex {1/4}$ שיטחו של $latex {c}$.
הערות לסיכום ותודות; הפרדוקס של ברטרן
מאמר זה חייב תודה, קודם כל, למדען הצרפתי מהמאה ה-$latex {18}$ בופון, שהוענק לו תואר רוזן $latex {(Comte de Buffon, 1707-1788)}$ , שהציג את שאלתו המפורסמת הבאה:
נתונים קווים מקבילים במישור במרחקים $latex {d}$. מפילים באקראי מחט באורך $latex {a}$,$latex {(a<d)}$. מה ההסתברות שהמחט תחתוך את אחד הקווים.
בהתאם למשפט 1, התשובה היא
$latex \displaystyle \dfrac{2a}{\pi d}.$
(אין הבדל בתוצאה אם "מפילים" מחט אקראית על מערכת קווים מקבילים קבועה או מערכת קווים מקבילים אקראית על מחט קבועה!)
במאה ה-$latex {19}$ השתמשו בנוסחה זו לקבוע באופן ניסיוני את ערכו של $latex {\pi}$ עד דיוק של מספר ספרות אחרי הנקודה!
ותודה גם לפרופ' גיל קלעי מהאוניברסיטה העברית, שמהרצאה שלו בטכניון למדתי איך מוכיחים שלכל העקומים הקמורים בעלי רוחב קבוע $latex {d}$ יש אותו היקף $latex {\pi d}$, כמו שהובא לעיל.
ולסיום אזהרה:
אנו עסקנו במה שלפעמים קוראים "הסתברות גיאומטרית". אצלנו ההסתברות נקבעה באופן יחיד ע"י דרישת האינווריאנטיות לגבי הזזות וסיבובים. אבל אם אין אינווריאנטיות ברורה כזו, יכולים ליפול בפח, כמו שמראה הדוגמה המפורסמת הבאה של המתמטיקאי הצרפתי ברטרן $latex {(Joseph Bertrand, 1822-1900)}$.
פרדוקס ברטרן.

נתון מעגל $latex {\Gamma}$ בעל רדיוס $latex {R}$. מה ההסתברות שמיתר אקראי $latex {c}$ ב-$latex {\Gamma}$ יהיה יותר ארוך מצלע המשולש שווה הצלעות החסום ב $latex {\Gamma}$?
"פיתרון" 1. למיתר יש מרחק מהמרכז, שמשתנה על הקטע $latex {[0,R]}$. המיתר יקיים את התנאי אם המרחק שייך ל- $latex {[0,\frac12 R]}$. לכן התשובה היא $latex {1/2}$.
"פיתרון" 2. המיתר נקבע ע"י קשת המעגל שהוא פורש. הזווית המרכזית של קשת זו משתנה על הקטע $latex {[0,\pi]}$. המיתר יקיים את התנאי אם הזווית המרכזית של הקשת שייכת ל- $latex {[\frac23\pi,\pi]}$. לכן התשובה היא $latex {1/3}$.
"פיתרון" 3. מיתר נקבע ע"י האמצע שלו, שמשתנה על העיגול של $latex {\Gamma}$. המיתר יקיים את התנאי אם האמצע שלו נמצא בעיגול עם אותו מרכז כמו $latex {\Gamma}$ וחצי הרדיוס, ששיטחו, כמובן, רבע שטח $latex {\Gamma}$. לכן התשובה היא $latex {1/4}$.
למעשה חושבו כאן הסתברויות לגבי "מידות הסתברות" שונות (בקבוצת המיתרים). כולן אינווריאנטיות לגבי סיבוב המעגל, אבל מאחר שחבורת הסיבובים לא "טרנזיטיבית" - לא כל שני מיתרים מועתקים זה לזה ע"י סיבוב - אינווריאנטיות זו לא מספיקה כדי לקבוע את "המידה הההסתברותית" באופן יחיד.
$latex {^1}$ המונח הטכני ל"מדידה" אקראית כזו הוא: "משתנה סטוכסטי", או "משתנה אקראי".
מחלקה למתמטיקה ניסויית נפתחה בטכניון
אנה ליזהטוב
מחלקה למתמטיקה ניסויית נפתחה בטכניון
19 במאי 2014
באחת מקומות הקרקע של בניין הפקולטה למתמטיקה בטכניון פגשה כתבתנו אנה ליזהטוב את נציגה (היחיד, בינתיים) של מחלקה חדשה שנפתחה בטכניון, המחלקה למתמטיקה ניסויית. הנציג, ד״ר יסולא פז, חזר לפני כחודש מארצות הברית, שם כתב את עבודת הדוקטורט שלו בנושא ״המספרים המרוכבים ־ ממשות מול דמיון״. הוא נלהב מן האפשרויות שהטכניון פתח לפניו. ״זהו תחום חדש, שעדיין לא זכה להכרה הראויה, ואני נרגש מן הפתיחות של אנשי הפקולטה למתמטיקה שקבלוני כשווה בין שווים״, אמר ד״ר פז, כשהוא מוחה דמעת התרגשות מזווית עינו בידו האחת, בעוד ידו השנייה עסוקה בסידור ניירות על שולחנו.
הד״ר פז מלא תוכניות כרימון. פרויקט אחד שהוא מתכנן הוא להעסיק סטודנטים בהטלת קוביות כדי לבדוק באורח ניסויי את חוקי ההסתברות הידועים, ולגלות חוקים חדשים, אם עדיין קיימים כאלה. מטעמים הומניטריים יועסקו בכך הסטודנטים תוך משחק שש־בש.
תוכנית אמביציוזית נוספת היא פרויקט משותף עם המחלקה לחקר השינה שבפקולטה לביו־רפואה. בפרויקט הזה ינסו לגלות מספרים שאנשים חולמים עליהם תכופות.
״כשאדם חולם על מספר יש לכך סיבה לא מודעת, ובדרך כלל זוהי תכונה מעניינת של המספר, טוען ד״ר פז. ״האם שמת לב לכך שכאשר מבקשים מתמטיקאים להמציא מספר אקראי הם בוחרים בדרך כלל במספר $latex {17}$? ואכן $latex {17}$ ידוע כבעל תכונות מעניינות במיוחד. למשל, הוא מספר ראשוני השווה לסכום המספרים הראשוניים הקטנים מחציו. דרך החלומות אנחנו מקווים לגלות מספרים מעניינים חדשים״.
תוכנית נוספת של ד״ר פז היא ליישב פרדוקס ידוע מתורת הקבוצות. אם תבקש אדם לבחור מספר טבעי אקראי, מהו הסיכוי שיבחר במספר שמתחלק ב־$latex {3}$? כמובן,שליש. (המדובר באדם, לא במתמטיקאי. כשמדובר במתמטיקאי הסיכוי הוא אפס,משום שכאמור הוא יבחר במספר $latex {17}$). אבל תשובה הגיונית לא פחות היא ״חצי״, משום שמחצית מן המספרים הטבעיים מתחלקים ב־$latex {3}$. תיווכחו בזאת אם תכתבו את המספרים הטבעיים בשתי שורות:
$latex {1 2 4 5 7 \dots}$
$latex {3 6 9 12 15 \dots}$
כנגד כל מספר המתחלק ב־$latex {3}$ יש מספר שאינו מתחלק ב־$latex {3}$, ואם כן בדיוק חצי מן המספרים הטבעיים מתחלקים ב־$latex {3}$. זוהי תגלית של המתמטיקאי גיאורג קנטור (1925 − 1850). ״אנו נחושים בכוונתנו לגלות את האמת״, אומר ד״ר פז בעיניים בורקות, ״ונעשה זאת בניסוי שבו יתבקשו סטודנטים אקראיים לבחור מספרים אקראיים. אם יהיה צורך נטאטא את התיאוריות של קנטור אל מחוץ לספרי הלימוד״.
הפרוייקט האחרון שעליו הסכים ד״ר פז להרחיב את הדיבור שייך לתחום מתמטי הקרוי ״תורת האינפורמציה״. מה שמלמד אותנו התחום הזה הוא שככל שפיסת מידע מכילה יותר אינפורמציה כך היא נדירה יותר. ״מוכר לך בוודאי״ אמר לי ד״ר פז בקולו הדידקטי ״הסיפור של אדינגטון, על הקוף היושב ומתקתק אקראית במכונת כתיבה. אם ישב מספיק זמן, בסבירות גדולה יתקתק בין השאר גם את ״המלט״ של שייקספיר. עתה, מה מכיל אינפורמציה רבה יותר מאשר הוכחה מתמטית? אם כן, לפי תורת האינפורמציה מעטים הסיכויים שגיבוב מקרי של מילים יצטרף להוכחה מתמטית. אנחנו מתכוונים לבדוק את התיזה הזאת באורח ניסויי, ונעשה זאת בכך שנעבור על מחברות הבחינה של חשבון דיפרנציאלי 1 מחמש השנים האחרונות״. בשלב זה נרדם הד״ר פז ממאמץ הראיון.
הערה: בתשובה לפניית כתבנו הכחיש דיקן הפקולטה למתמטיקה כל היכרות עם הד״ר פז או כל ידיעה על המחלקה למתמטיקה ניסויית.
חידה לגדולים
רון אהרוני
שלוש חידות לגדולים
- הוכיחו שבהינתן $latex {n}$ נקודות במישור שאינן כולן על ישר אחד, יש ישר שעובר דרך בדיוק שתיים מהן. האם תוכלו להוכיח שיש שניים כאלה? ושלושה?
- בליגת כדורסל משחקת כל קבוצה בדיוק פעם אחת עם כל קבוצה אחרת. הוכיחו שאפשר לסדר את כל הקבוצות בסדר שבו הראשונה ניצחה את השנייה, שניצחה את השלישית, שניצחה את הרביעית, וכו' - עד לאחרונה.
- אחרי כמה סיבובים בליגה עדיין לא שיחקה כל קבוצה עם כל קבוצה. חלק מן הזוגות שיחקו, וחלק לא. הראו שיש קבוצה $latex {S}$ של קבוצות, שיש לה את התכונות הבאות:א. בין איברי $latex {S}$ לא נערכו בכלל משחקים.ב. לכל קבוצה $latex {a}$ שאינה ב-$latex {S}$ יש קבוצה ב-$latex {S}$ שאו שניצחה בעצמה את $latex {a}$, או ניצחה קבוצה שניצחה את $latex {a}$.
חידות לילדים
קוונט - תרגום : אירנה גורליק עריכה: מיכאל אנטוב
1. מוצג מטה חישוב בטור של כפל של שני מספרים. חלק מהספרות נמחקו והוחלפו על ידי כוכבים. נסו לשחזר את המספרים החסרים.
*2*
7 *
* * *
* * * *
8 * * * *
2. בפינה השמאלית התחתונה של לוח שחמט שמו כלי דמקה. שני שחקנים מזיזים אותה לפי התור לריבוע השכן. הכיוונים המתוארים הם אלו המסומנים באיור.
מנצח זה שבתורו מגיע למשבצת הימנית העליונה. מה צריכה להיות האסטרטגיה של השחקן הראשון כדי לנצח?
3. נסו להקיף את הצורה שבאיור מבלי להרים את העיפרון מהדף ובלי לעבור על אותו קו פעמיים.

4. סכום של המחוסר, המחסר וההפרש שווה ל-624. מצאו את המחוסר, המחסר וההפרש אם ההפרש קטן ב-56 מהמחסר.

