נטגר גליון 6
דבר העורך
רון אהרוני
בגיליון הזה יש ארבעה מאמרים, שמכסים חמישה תחומים: גיאומטריה, מספרים, היסטוריה של המתמטיקה, חשבון דיפרנציאלי ואינטרגלי, וכהרגלנו - דמות של חוקר מתמטי. כיצד מכסים ארבעה מאמרים חמישה תחומים? ובכן - מאמרו היפה של אליהו לוי, על הגיאומטריה ביפן בזמן שהייתה מסוגרת מן המערב, מכיל גם סיפור היסטורי מעניין. גם מאמרו של וויליאם דיוק, מתורגם בידי משה ברוך מן הפקולטה למתמטיקה בטכניון, עוסק מעט בהיסטוריה של המתמטיקה. הוא מדבר על השערה יפהפיה של פייר דה פרמה ($latex {Fermat}$) - לא זו הידועה ביותר, אלא על "מספרים פוליגונליים" (תצטרכו לקרוא את המאמר כדי לדעת מהם!). מצד הביוגרפיה, אנחנו ממשיכים עם עלילותיו של המתמטיקאי הניסויי יסולא פז. לאחרונה יצא עם תגלית מרעישה, בדבר גדלו של המספר הידוע אפסילון. כדי להסביר את חשיבותה של התגלית הזאת, הואילה אנה ליזהטוב בטובה להוסיף מאמר על "מה זה אפסילון", שהוא בעצם מאמר על ההיסטוריה של החשבון הדיפרנציאלי והאינטגרלי.
וכרגיל, יש גם חידה לגדולים, הפעם באדיבותו של רום פנחסי.
אתם רואים - מעט המחזיק את המרובה!
כמו כולם, גם "נטגר" יוצא לפגרת קיץ, למשך חודשיים. חופש נעים לכולכם.
סקופ! מיוחד ל"נטגר"! חושב ערכו המדויק של אפסילון!
אנה ליזהטוב
בגליוננו הקודם פרסמנו ראיון עם ד"ר יסולא פז, מיסד המחלקה למתמטיקה ניסויית בטכניון. כזכור, ד"ר פז סיפר על תכניותיו למחקר. מאז, מתברר, לא שקט הד"ר פז על שמריו, ולאחרונה יצא בתגלית מרעישה: הוא הראשון, כנראה, שמצא את ערכו המדויק (עד כדי דלתא) של אחד הגדלים המתמטיים הידועים ביותר, הלא הוא האפסילון!
כזכור, לא היתה מציאת האפסילון בין תכניותיו של הד"ר פז, והוא עלה על התגלית, אפשר לומר, במקרה. "מחקר מתמטי" אומר ד"ר פז בחיוך מבויש קמעא, "אינו מתנהל על פי תכנון מוגדר מראש. יש שאתה מחפש אתונות ומוצא מלוכה (אף על פי שבדרך כלל קורה ההפך) וזה, אם יורשה לי להעיד על עצמי, מה שקרה לי הפעם."
מתברר שמציאת האפסילון התאפשרה רק תודות לשיטה הניסויית במתמטיקה, שהד"ר פז הוא אחד מחלוציה. "אפסילון" מסביר ד"ר פז "הוא כידוע מספר חיובי קטן כרצוננו. הבעיה במציאתו עד היום היתה שלא ברור היה רצונו של מי. והנה, לילה אחד, בשעה שעסקתי בבעיה אחרת לגמרי, על היפוך מטריצות בעזרת מחוגה וסרגל, עלה במוחי הפתרון הפשוט" (הגאוני בפשטותו, יורשה למערכת להוסיף) "רעיון שנולד מרוחה של המתמטיקה הניסויית - לשאול אנשים לרצונם! ומכיון שאיננו יכולים לשאול את פיהם של כל יושבי תבל, ערכנו מדגם בטכניון, ואת האפסילון המדויק (כאמור, בקירוב של דלתא) חישבנו על פי נוסחת אקסטרפולציה מסובכת שמצאתי בספר אלגברה מן המאה שעברה."
לרבים מן הסטודנטים זכורה בוודאי דמותו של אדם שהתהלך בטכניון עם פנקס שחור בידו וברק של שליחות בעיניו, ושאל "כמה קטן ברצונך שאפסילון יהיה?" זה היה, עכשיו מותר לגלות, הד"ר פז. "לא היתה זו משימה קלה" נזכר ד"ר פז בעיניים לחות. "לא אחת זכיתי בקיתונות של לעג, ומי ימנה את מספר הסטירות שספגתי מידי סטודנטיות נזעמות בתגובה לשאלתי. קרה גם פעם" הוסיף כשצל של מרירות בקולו, "שמישהו הזמין ניידת מבית החולים לחולי נפש. אבל ידעתי שזהו גורלם של חדשנים, ולא נרתעתי. לבסוף, כשהמדגם היה גדול מספיק, שלחתי את התוצאות למכון למתמטיקה ניסויית בפרינסטון, שאישרו את ממצאי."
כידוע, אין פרס נובל במתמטיקה, בגלל קשריו האינטימיים מדי של מתמטיקאי, ידידו של נובל, עם אשתו של נובל. אבל, על פי עדות מומחים, תגליתו של ד"ר פז היא ברמה אחת עם תגליות שזכו בפרס. ד"ר (בקרוב פרופסור?) פז עצמו נמנע, בינתיים, מזרקורי הפרסומת. בעיניים מושפלות הוא אומר: "אם הקלתי בתגליתי, ולו במעט, על סבלותיהם של תלמידי חדו"א, כי אז באתי על שכרי."
הערת המערכת: הערך המחושב של אפסילון הוא כה קטן, עד כי אין טעם לפרסמו.
מה זה "אפסילון"
אנה ליזהטוב
כשהמתמטיקאי ההונגרי הגדול פאול ארדש היה פוגש ילד, היה נוהג לשאול "בן כמה האפסילון הזה?" אם הייתה זו ילדה, הוא היה שואל "בת כמה הדלתא הזאת?" לאחר שקיבל תשובה היה מראה לילד או לילדה טריק קטן עם מטבעות, ואחר כך היה פונה לעיסוקים האמיתיים, המתמטיים.
למה "אפסילון" ו"דלתא"? משום שבמתמטיקה שתי האותיות היווניות האלה, $latex {\varepsilon}$ ו-$latex {\delta}$, מציינות גדלים "קטנים". מה זה "קטנים"? ובכן, הכוונה אינה למיליונית או ל-$latex {10^{-80}}$. לצורך ענייננו כאן, הכל יחסי. גם $latex {1}$ וגם מיליון יכולים להיות מספרים "קטנים". תלוי ביחס למה. וה"מה" הזה הוא "כמה אנחנו רוצים שהמספר יהיה קטן, כדי שהוא יקיים תנאי מסוים"
אז מה זה "קטן"? בשביל זה צריך לחזור לפרק מעניין בהיסטוריה של המתמטיקה, המצאת החשבון הדיפרנציאלי והאינטגרלי - ה"חדו"א". מי המציא את החדו"א? ובכן, הגינות מחייבת לייחס זאת ליוונים העתיקים. למעשה, הם המציאו את החשבון האינטגרלי לפני שהמציאו את החשבון הדיפרנציאלי. בחשבון האינטגרלי מחלקים את העולם לחלקים קטנים, ומסכמים גדלים שמתאימים להם. למשל, את שטחיהם.
כדי לחשב את שטח העיגול היוונים חילקו את העיגול לגזרות צרות רבות. מכיוון שהבסיס של כל גזרה קטן, הוא מתנהג כמו ישר, ולכן הגזרה היא בקירוב טוב משולש, ולכן שטחה הוא בקירוב טוב מאוד אורך הבסיס כפול הגובה, חלקי $latex {2}$. הגובה הוא, כמובן, הרדיוס $latex {R}$ של העיגול. סכום שטחי הגזרות הוא אם כן סכום אורכי הבסיסים כפול הרדיוס, חלקי $latex {2}$. ומכיוון שסכום אורכי הבסיסים הוא היקף המעגל, שהוא $latex {2\pi R}$ (זוהי הגדרת $latex {\pi}$ - כאן אין מה להוכיח!) הרי שטח העיגול הוא $latex {\frac{1}{2}2\pi R \times R}$, שהוא $latex {\pi R^2}$ - הנוסחה המוכרת לשטח העיגול. בצורה דומה ידעו היוונים לחשב את נפח הכדור ($latex {\frac{4}{3}\pi R^3}$) ואת שטח הפנים שלו ($latex {4\pi R^2}$).
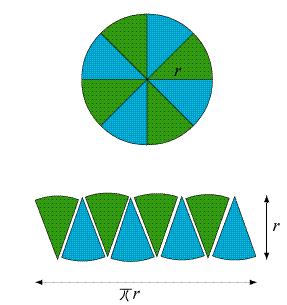
בציור ממלאים בעזרת המשולשים תחום כמעט מלבני, ורואים מהו השטח מכך - בסיס המלבן הוא חצי מהיקף המעגל, וגובהו הור רדיוס המעגל. אם כן שטח העיגול הוא הרדיוס כפול חצי ההיקף.
זהו הרעיון של החדו"א - כשמסתכלים על מעגל, או על עקום חלק, מקרוב מאוד, הוא נראה כמו קו ישר. זוהי הסיבה שהקדמונים חשבו שהעולם שטוח. אנחנו מסתכלים על כדור הארץ מקרוב, ואנחנו רואים רק חלק קטן מאוד ממנו, ומנקודת ראות כזו הוא נראה שטוח. מישהו אמר פעם ש"החשבון הדיפרנציאלי והאינטגרלי הומצאו על ידי מי שחשב שהעולם שטוח, וצדק".
אחר כך התחדש החדו"א במאה ה-$latex {16}$, והגיע לבשלות, לפחות מבחינה חישובית, במאה ה-$latex {17}$, בתגליותיהם של פרמה ($latex {Fermat}$), ניוטון ולייבניץ. אבל הבשלות הייתה רק חישובית. אף אחד לא ניסח במדויק מה פירוש "לראות את העיגול מקרוב" - כמה קרוב? המושג המרכזי של החדו"א - הגבול, כלומר התקרבות של מספרים למספר נתון, לא הוגדר מעולם. הוא התקבל כמובן מאליו, והובן רק אינטואיטיבית. למשל העובדה שסדרת המספרים $latex {\frac{1}{n}}$, כלומר הסדרה
$latex \displaystyle \frac{1}{1}, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}\ldots$
שואפת לגבול שהוא המספר $latex {0}$, עובדה שברורה לכל מי שמסתכל בסדרה, לא הוגדרה מעולם.
ואז, במאה התשע עשרה, נוכחו המתמטיקאים לדעת שלא יוכלו להתחמק מהגדרות מדויקות. מהי ההגדרה? האם הסיבה לשאיפת הסידרה ל-$latex {0}$ היא שמרחקם של כל המספרים האלה מ-$latex {0}$ יותר קטן מ-$latex {1}$? בוודאי שלא. קירבה של $latex {1}$ עשויה לספק לצרכים מסוימים, ולא להיות מספיקה לצרכים אחרים. אם כן, מהי ההגדרה?
התשובה היא - איברי הסדרה קרובים כרצוננו. כלומר, לכל מידת קירבה, המספרים יהיו קרובים ל-$latex {0}$ יותר מן המידה הזאת, החל ממקום מסוים.
למידת הקירבה הזאת קוראים "אפסילון" - ה-$latex {e}$ היוונית. מדוע? אין לי מושג. אולי מפני שהאותיות היווניות שקודמות לה, $latex {\alpha, \beta, \gamma, \delta}$ (אלפא, בתא, גמא, דלתא - המקבילות של אלף, בית, גימל ודלת העבריות) היו כבר תפוסות. ובכן, ההגדרה היא שהסדרה $latex {\frac{1}{n}}$ שואפת ל-$latex {0}$ משום שלכל מספר $latex {\varepsilon}$ חיובי מרחקם של איברי הסדרה מ-$latex {0}$ קטן מ-$latex {\varepsilon}$ החל ממקום מסוים. למשל, אם תקחו $latex {\varepsilon=\frac{1}{1000}}$, יהיו איברי הסדרה קרובים לגבול, $latex {0}$, יותר מ-$latex {\varepsilon}$ החל מן המקום ה-$latex {1001}$.
עכשיו אולי תבינו את חשיבות תגליתו של ד"ר פז, שעליה יסופר במדורנו הפעם.
גיאומטריית המקדשים היפנית
אליהו לוי
בין השנים 1639 עד 1854 סגרו השוגונים מבית טוקוגאווה את יפן באופן הרמטי מהעולם החיצון. בין השאר רעיונות מערביים, ביניהם הישגי ההתעוררות המדעית באירופה, לא יכלו כמעט לחדור ליפן. אבל בתקופת בידוד זו המשיכה התרבות היפנית להתפתח מתוך עצמה.
בתקופה זו, אוהבי מתמטיקה יפנים, סמוראים, סוחרים ואיכרים, היו מציגים ופותרים בעיה, בדרך כלל גיאומטרית, מציירים את הבעיה בצבעים בלוחית עץ יפהפיה, שנקראה sangaku (לוחית מתמטית), ותולים אותה תחת גגו של בניין מקודש. היתה זו גם העלאת מנחה לישות עליונה, וגם הצגת אתגר בפני באי המקדש: נראה אם תפתרו זאת! במאות ה 18 וה 19 הופיעו ביפן ספרים שאספו sangaku כאלה. לוחיות וספרים אלה הם באותה מידה קובצי בעיות מתמטיות כמו יצירות אמנות מרהיבות.
על הsangaku אפשר לקרא במאמר שהופיע ב Scientific American, גליון מאי 1998, שבו מובאות דוגמאות עם תמונות ורפרודוקציות של לוחיות.
לרוב בעיות ה sangaku יש סגנון מיוחד. הן מרבות לעסוק במעגלים, ריבועים, אליפסות, וכדורים במרחב, הנוגעים זה בזה. הבעיה הבאה, שמופיעה בעמ' 65 במאמר הנזכר, שונה קצת מהשאר. זהו משפט גיאומטרי מעניין, שלא ראיתי בשום מקום אחר. אביא הוכחה שלו בעזרת גיאומטריה אנליטית, אבל לא ידועה לי הוכחה "גיאומטרית" שלו. אשמח מאוד אם הקוראים ימצאו וישלחו הוכחה "גיאומטרית" כזו. (למרות שסיינטיפיק אמריקן הבטיחו לפרסם פתרון של הבעיות באתר שלהם, אני לא הצלחתי למצוא את זה שם).
להוכיח את המשפט הבא: יהי $latex {AB}$ הקוטר של מעגל $latex {\mathcal{M}}$, ותהי $latex {C}$ נקודה על $latex {AB}$. יהי $latex {\mathcal{N}}$ המעגל שקוטרו $latex {AC}$ ונבנה משולש שווה-שוקיים $latex {\triangle CKB}$ שבסיסו הוא $latex {CB}$ וקודקודו $latex {K}$ נמצא על המעגל $latex {\mathcal{M}}$. יהי $latex {\mathcal{L}}$ מעגל המשיק מבפנים ל $latex {\mathcal{M}}$, ומבחוץ ל $latex {\mathcal{N}}$ ול $latex {\triangle CKB}$. אז מרכזו $latex {L}$ של $latex {\mathcal{L}}$ נמצא בדיוק מעל ל $latex {C}$, כלומר הישר $latex {LC}$ מאונך ל $latex {AB}$.

הוכחה בעזרת גיאומטריה אנליטית: יהיו $latex {M}$ ו $latex {N}$ מרכזי $latex {\mathcal{M}}$ ו $latex {\mathcal{N}}$ בהתאמה, ויהי $latex {D}$ אמצע $latex {CB}$. נבחר מערכת צירים בעלת מרכז $latex {M}$ בה רדיוס $latex {\mathcal{M}}$ הוא $latex {1}$, ויהי רדיוס $latex {\mathcal{N}}$ שווה ל $latex {r}$. מכיוון ש $latex {N}$ הוא אמצע $latex {AC}$ ו $latex {D}$ הוא אמצע $latex {CB}$, $latex {ND=\frac12\cdot AB=1}$. מכאן, ומכך ש $latex {AM=1}$ נובע ש $latex {MD=AN=r}$. במשולש ישר-הזווית $latex {MDK}$ היתר $latex {MK=1}$ ו $latex {MD=r}$, ולכן, לפי משפט פיתגורס $latex {DK=\sqrt{1-r^2}}$. תהי $latex {\alpha:={<\!\!\!)}KCB}$. אז
$latex \tan\alpha = \displaystyle \dfrac{KD}{CD}=\dfrac{\sqrt{1-r^2}}{1-r}=\sqrt{\dfrac{1+r}{1-r}}$
$latex \cos\alpha = \displaystyle \sqrt{\dfrac1{1+\tan^2\alpha}}=\sqrt{\dfrac1{1+\dfrac{1+r}{1-r}}}=\sqrt{\dfrac{1-r}2} $
נזכיר ששיעורי $latex {C}$ הם $latex {C=(2r-1,0)}$, כי $latex {A=(-1,0)}$ ו $latex {AN=NC=r}$.
תהי כעת $latex {L'}$ הנקודה ששיעוריה
$latex \displaystyle L'=\left(2r-1,\dfrac{2r}{1+r}\sqrt{2(1-r)}\right)$
ברור ש $latex {L'C}$ מאונך ל $latex {AB}$. המשפט יוכח אם נוכיח ש $latex {L'}$ היא המרכז $latex {L}$ של $latex {\mathcal{L}}$, כלומר שהמרחקים מ $latex {L'}$ למעגל $latex {\mathcal{M}}$, למעגל $latex {\mathcal{N}}$ ולישר $latex {CK}$ שווים.
מרחקו של $latex {L'}$ מהישר $latex {CK}$ הוא:
$latex \displaystyle L'C\cdot\cos\alpha=\dfrac{2r}{1+r}\sqrt{2(1-r)}\cdot\sqrt{\dfrac{1-r}2}=\dfrac{2r(1-r)}{1+r}.$
מרחקו של $latex {L'}$ מהמעגל $latex {\mathcal{M}}$ הוא:
$latex \displaystyle 1-L'M=1-\sqrt{(2r-1)^2+\left(\dfrac{2r}{1+r}\right)^2\cdot2(1-r)}=$
$latex 1-\dfrac1{1+r}\sqrt{(1+r)^2(2r-1)^2+8r^2(1-r)}=$
$latex \displaystyle =1-\dfrac1{1+r}\sqrt{(2r^2-(1-r))^2+8r^2(1-r)}=$
$latex 1-\dfrac1{1+r}\sqrt{(2r^2+(1-r))^2}= 1-\dfrac{2r^2+1-r}{1+r}=$
$latex \displaystyle =\dfrac{1+r-2r^2-1+r}{1+r}= \dfrac{2r(1-r)}{1+r}. $
(יש לבחור את השורש החיובי, ואכן $latex {2r^2+1-r=(1-\frac12r)^2+\frac74r^2>0}$).
ולבסוף, מרחקו של $latex {L'}$ מהמעגל $latex {\mathcal{N}}$ הוא ( נזכיר ש $latex {N=(-1+r,0)}$):
$latex \displaystyle \sqrt{r^2+\left(\dfrac{2r}{1+r}\right)^2\cdot2(1-r)}-r= r\left(\sqrt{1+\dfrac{8(1-r)}{(1+r)^2}}-1\right)=$
$latex r\left(\sqrt{\dfrac{(1+r)^2+8(1-r)}{(1+r)^2}}-1\right)=$
$latex \displaystyle =r\left(\sqrt{\dfrac{r^2-6r+9}{(1+r)^2}}-1\right)= r\left(\dfrac{3-r}{1+r}-1\right)=r\dfrac{2-2r}{1+r}= \dfrac{2r(1-r)}{1+r}. $
(יש לבחור את השורש החיובי $latex {3-r}$).
ובכך הוכח המשפט.
האם הקוראים יכולים למצוא הוכחה "גיאומטרית"?
בעיות ישנות ותוצאות חדשות על תבניות ריבועיות
וויליאם דיוק, Notices of the AMS vol. 44, 1997 תרגם: משה ברוך
הקדמה
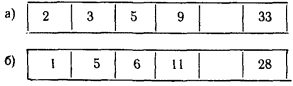
האם כל מספר הוא סכום של שני ריבועים של מספרים שלמים? בוודאי שלא. הוכיחו לעצמכם שאם מספר משאיר שארית 3 בחלוקה ב-4 אז הוא לא סכום של שני ריבועים. כך, 3, 7, 11, 15 וכו' אינם סכומים של שני ריבועים. האם כל מספר הוא סכום של שלושה ריבועים שלמים? גם זה לא. 7 איננו סכום כזה. 11 כ ן: הוא שווה ל-9+1+1. נסו והיווכחו ש- 15 אינו סכום של שלושה ריבועים. (מה אם מרשים גם הפרשים?)
אחד המשפטים המפורסמים על מספרים שלמים הוא של לגרנז' –
כל מספר שלם הוא סכום של ארבעה ריבועים שלמים.
במאמר הזה נספר קצת על ההיסטוריה המרתקת של המשפט הזה, ועל משפטים שקשורים אליו.
טענה של פרמה
ב 1638 שיער פרמה שכל מספר טבעי הוא סכום של לכל היותר שלושה מספרים משולשים, ארבעה ריבועים, חמישה מספרים מחומשים וכו. מהם כל המספרים האלה, הקרויים על שמות צורות גיאומטריות? הנה ההגדרה:
מספרים משולשים הם המספרים $latex { 1,3,6,10,\dots,\frac{n^2+n}{2},\dots }$ . מספרים ריבועים הם המספרים $latex { 1,4,9,116,\dots,n^2,\dots }$ מספרים מחומשים הם המספרים $latex { 1,5,12,22,\dots,\frac{3n^2-2}{2},\dots }$ מספרים משושים הם המספרים $latex { 1,6,15,28,\dots,2n^2-n,\dots }$. באופן כללי, מספר פוליגונאלי מסדר $latex { k } $ נתון על ידי $latex { \frac{(k-2)n^2-(k-4)n}{2} } $
ההשערה של פרמה יפה במיוחד משום שהיא חדה. לכל k יש מספרים שאינם מיוצגים כסכום של פחות מ-k מספרים פוליגונאליים מסדר k. דוגמה לכך הוא המספר 2k-1 .
במכתב שכתב פרמה לפסקל ב-1654 הוא תיאר את הטענה הזו כתוצאה החשובה ביותר שלו. כמו במקרה המפורסם יותר, של ההשערה שזכתה לשם "השערת פרמה" או "המשפט האחרון של פרמה", הוא כנראה השלה את עצמו. במיוחד קשה להאמין שהייתה לו הוכחה נכונה עבור שלושה מספרים משולשים.
ראשונה להיפתר בצורה מלאה הייתה הטענה שכל מספר טבעי הואסכום של ארבעה ריבועים. היא הוכחה על ידי לגרנג' ב-1772 בעזרת רעיונות של אוילר.
הבא בתור היה המקרה של שלושה מספרים משולשים. לפני כמאתיים שנה התחיל גאוס לכתוב את היומן המתמטי שלו. בין הרישומים הראשונים שלו מופיע:
מספר $latex {\Delta+\Delta+\Delta =} $ יוריקה!
כלומר – כל מספר הוא סכום של שלושה מספרים משולשים – מצאתי! כאמור, הטענה הזאת פירושה ש:
$latex {m = \frac{n_1^2+n_1}{2}+\frac{n_2^2+n_2}{2}+\frac{n_3^2+n_3}{2}} $ עם שלמים אי שליליים שבהעברת אגפים פירושו: $latex { 8m+3 = (2n_1+1)^2+(2n_2+1)^2+(2n_3+1)^2 }$ t אם כן, הטענה של גאוס שקולה לטענה שכל מספר מהצורה $latex { 8m + 3 } $ הוא סכום של שלושה ריבועים של מספרים אי זוגיים. זהו מקרה פרטי של תוצאה כללית יותר, שמספר הוא סכום של שלושה ריבועים בדיוק כאשר הוא אינו מהצורה$latex { 4^b(8m+7) } $ . הטענה הזאת שוערהעל ידי לג'נדר ב 1798 . ב-1801 נתן גאוס הוכחה מלאה לטענה זו בספרו המפורסם "מחקרים אריתמטיים" (Disquisitiones Arithmeticae) .
ב- 1813 פתר קושי את ההשערה של פרמה במלואה. הוא הראה שההשערה הכללית נובעת מהמשפט על המספרים המשולשים.
זמן מה לאחר ההוכחה של קושי, דיריכלה מצא נוסחה יפה למספר האפשרויות שבהן מספר $latex {m} $ מיוצג כסכום של שלושה מספרים משולשים. במקרה המיוחד שבו $latex {8m+3} $ הוא מספר ראשוני, נוסחה זו אומרת שמספר זה הוא ההפרש בין מספר השרשים הריבועיים מוד $latex {8m+3} $ למספר אלו שאינם שרשים ריבועיים מוד $latex {8m+3} $ בקטע מ $latex {1} $ עד $latex {4m+1} $ . לדוגמא, אם $latex {m=2} $ אז $latex {8m+3=19} $ ויש ששה שרשים ריבועיים מוד $latex {19} $ בקטע מ $latex {1} $ עד $latex {4m+1=9} $ שהם $latex {1,4,5,6,7,9} $ ושלושה מספרים שאינם שרשים ריבועיים שהם $latex {2,3,8} $ . לכן יש שלוש דרכים להציג את $latex {2} $ כסכום של שלושה מספרים משולשים: $latex {2=1+1+0=1+0+1=0+1+1} $
עדיין נשארו בעיות פתוחות רבות על המספרים האלה. לג'נדר בספרו "תורת המספרים" מ1830 הוכיח באמצעים אלמנטריים שכל מספר גדול מ 1791 הוא סכום של ארבעה מספרים משושים (הקסגונליים). תוצאה זו הובילה לשאלה האם אפשר להסתפק בשלושה מספרים הקסגונליים ממקום מסוים ואילך. ואכן, כך הוא:
משפט(דיוק ושולץ-פילו 1990): קיים מספר טבעי שהחל ממנו כל מספר טבעי הוא סכום של שלושה מספרים הקסגונליים.
מאמר של רמנוג'ן
ב-1914, רמנוג'ן פרסם מאמר [8] שהיה לו השפעה גדולה על המחקר בנושא של ייצוג מספרים על ידי תבניות ריבועיות. הוא חיפש את כל השלמים $latex {0\le a \le b \le c \le d} $ כך שכל מספר טבעי מיוצג על ידי התבנית: $latex {ax_1^2+bx_2^2+cx_3^2+dx_4^2} $ בדיקה אלמנטרית של כל המקרים האפשריים מראה שכדי שהמספרים $latex {1,2,3,5} $ ייוצגו אז $latex {(a,b,c)} $ צריכים להיות מבין $latex {(1,1,1),(1,1,2),(1,1,3),(1,2,2),(1,2,3),(1,2,4)} $ או $latex {(1,2,5)} $ . אף אחת מבין התבניות הריבועיות בשלושה משתנים $latex {ax_1^2+bx_2^2+cx_3^2} $ המתאימות לשלשות אלו אינה מייצגת את כל הטבעיים. המספרים הקטנים ביותר שאינם מיוצגים הם $latex {7,14,6,7,10,14,10} $ בהתאמה. (אחד לכל תבנית). על ידי בדיקת המספרים הללו בתבניות המתאימות עם ארבעה משתנים מגיעים ל- $latex {55} $ תבניות אפשריות. רמנוג'ן מצא כללים פשוטים לטבעיים שמיוצגים על ידי התבניות בשלושה משתנים ובעזרת הכללים הללו הראה שכל אחת מה $latex {55} $ התבניות עם ארבע משתנים מייצגת את כל הטבעיים. עשר שנים מאוחר יותר, דיקסון [3] שם לב שהתבנית המתאימה ל$latex {(1,2,5,5)} $ אינה מייצגת את $latex {15} $ אבל הוכיח שבשאר המקרים רמנוג'ן צדק ופרט בכללים שמצא עבור התבניות בשלושה משתנים. אפשר בקלות להכליל את הבעיה של רמנוג'ן לתבניות ריבועיות אחרות בשלושה משתנים. אפשר בקלות להכליל את הבעיה של רמנוג'ן לתבניות ריבועיות אחרות. תבנית ריבועית חיובית מסדר $latex { I } $ המקבלת ערכים שלמים היא פולינום הומוגני ריבועי $latex {Q(x) =Q(x_1,x_2,\dots,x_1) } $ עם מקדמים שלמים שמקיים $latex {Q(x) >0 } $ עבור $latex {x \neq 0} $ , $latex {x} $ ממשי. תבנית כזו מיוצגת בסימונים של מטריצות בצורה $latex {Q(x) = x^tAx} $ כאשר $latex {A=\frac{1}{2} \frac{\partial^2Q(x)}{\partial x_i\partial x_j}} $ היא מטריצה סימטרית חיובית. האיברים של $latex {A} $ הם חצי שלמים. אם כל האיברים של $latex {A} $ הם שלמים אז $latex {Q(x)} $ נקראת תבנית שלמה מטריציונית.
המילה האחרונה (בינתיים() בדבר השאלה אילו תבניות מייצגות את כל הטבעיים ניתנה על ידי קונווי ושניברגר [1] שהוכיחו:
משפט: אם תבנית ריבועית חיובית שלמה מטריציונית מייצגת את המספרים
$latex {1,2,3,5,6,7,10,14,15} $
אז היא מייצגת את כל הטבעיים.
השערה: אם תבנית חיובית עם ערכים שלמים מייצגת את כל אחד מהשלמים
$latex {1,2,3,5,6,7,10,13,14,15,17,19,21,22,23,26,29,30,31,34,35,37,42,58,93,110,145,203,290} $
אז היא מייצגת את כל הטבעיים.
במאמרו [8] רמנוג'ן מנסח את הבעיה של למצוא את כל התבניות החיוביות מהצורה $latex {ax_1^2+bx_2^2+cx_3^2+dx_4^2} $ שמייצגות כל מספר טבעי גדול מספיק. הוא טוען שהבעיה הזו היא קשה יותר ומעניינית יותר. בעיה זו נפתרה באופן מהותי על ידי קלוסתרמן ב-[6] ב-1926. המאמר של קלוסתרמן מהווה פריצת דרך בנושא. קלוסתרמן שיפר והכליל את שיטת המעגל בדרך שאפשרה לו לקבל תוצאה על ייצוג של שלמים בעזרת תבניות עם ארבעה משתנים. תוצאה זו הגיעה מחסם על סכומים שנקראים היום סכומי קלוסתרמן. הדוגמא הפשוטה ביותר לסכום קלוסתרמן הוא הסכום
$latex \displaystyle K(n,p)= \sum_{d=1}^{p-1} e^{2\pi in(d+\tilde{d})/p} $
כאשר $latex {p} $ הוא ראשוני ו$latex {\tilde{d}} $ הוא ההפיך הכפלי של $latex {d} $ מוד $latex {p} $. החסם של קלוסתרמן שהספיק בשביל השימוש לתבניות ריבועיות בארבעה משתנים שופר בהמשך על ידי החסם של וויל (Weil ) שהוא הטוב ביותר האפשרי:
$latex {|K(n,p)|\le2sqrt(p)} $
וויל הגיע לחסם הזה כמסקנה מההנחה של רימן עבור עקומים מעל שדה סופי שאותה הוכיח.
המאמר של רמנוג'ן גם פתח את הנושא הקשה יותר של תבניות שלושה משתנים. הוא כתב הערה במאמר על כך "שהמספרים הזוגיים שאינם מהצורה $latex { x^2 + y^2 +10z^2} $ הם כולם מהצורה $latex {4^k(16r+6)} $ (כלומר, כל מספר זוגי חיובי אחר מיוצג) בעוד שהמספרים האי זוגיים שאינם מיוצגים כמו
$latex {3,7,21,31,33,43,67,79,87,133,217,219,223,253,307,391,\dots} $
אינם מקיימים כלל ברור". דיקסון הוכיח את הטענה של רמנוג'ן בעזרת טיעון פשוט אבל השאלה אם קיימים אינסוף מספרים אי זוגיים שאינם מיוצגים נשארה פתוחה עד 1991. נובע מ[4] ש-
משפט: קבוצת המספרים האי זוגיים החיוביים שאינם מיוצגים על ידי התבנית של רמנוג'ן $latex { x^2 + y^2 +10z^2} $ היא קבוצה סופית.
גם במקרה הזה, ההוכחה אינה נותנת חסם מפורש על מספר היוצאים מן הכלל. בעצם, הרשימה של היוצאים מן הכלל של רמנוג'ן אינה מלאה, וגם המספרים $latex {679} $ ו $latex {2719} $ אינם מיוצגים. אונו ו סאונדררג'ן במאמר מרשים [7] הראו שאם מניחים את השערת רימן המוכללת אז אלו הם כל היוצאים מן הכלל.
ביבליוגרפיה
[1] J. H. Conway and W. Schneeberger, to appear.
[2] L.E. Dickson, History of the theory of numbers II, Chelsea Publishing, 1971.
[3] L.E. Dickson, Integers represented by positive ternary quadratic forms, Bull. Amer. Math. Soc. 33 (1927) 63-70.
[4] W. Duke and R. Schulze-Pillot, Representations of integers by positive ternary quadratic forms and equidistribution of lattice points on ellipsoids, Invent. Math. 99 (1990), 49-57.
[5] R. K. Guy, Every number is expressible as a sum of how many polygonal numbers?, Amer. Math. Monthly 101 (1994), 169-172.
[6] H. D. Kloosterman, On the representations of numbers in the form , Acta Math. 49 (1926), 407-464.
[7] K. Ono and K. Sounararajan, Ramanujan’s ternary quadratic form, Invent. Math. 130 (1997), 415-454.
[8] S. Ramanujan, On the expression of a number in the form , Collected papers, Chelsea.
חידה לגדולים
רום פנחסי
נתונות במרחב $latex {2014}$ נקודות כחולות ו-$latex {2014}$ נקודות אדומות. הוכיחו שסכום המרחקים בין כל $latex {2014^2}$ הזוגות של נקודות בצבעים שונים גדול או שווה לסכום כל המרחקים בין זוגות של נקודות כחולות, ועוד סכום כל המרחקים בין זוגות של נקודות אדומות.
רמז: פתרו זאת תחילה במקרה הפרטי שכל הנקודות נמצאות על אותו ישר.
חידות לילדים
קוונט - תרגום : אירנה גורליק