נטגר גליון 7
דבר העורך
רון אהרוני
לקוראים הנאמנים, וגם החדשים שהצטרפו זה עתה, שלום רב וברכת שנת לימודים פורייה.
כזכור, הבטחנו לעסוק מדי פעם גם בחינוך מתמטי. בגיליון זה יש שני מאמרים בכיוון הזה, שניהם של כתבתנו אנה ליזהטוב. האחד עוסק באמרה הידועה של איינשטיין, "אם אינך יכול להסביר את נושא מחקרך האחרון לילד בן שש, סימן שלא הבנת אותו". אנה ליזהטוב מנסה להבין אם יש משהו באמרה הזאת, או שהיא נאמרה עם קריצה ואין בה ממש (אני אישית לא מכיר מתמטיקאי שניסה להסביר את מחקריו לילד בן שש, וטוב שכך). ליזהטוב שואלת - האם אפשר להסביר לילד בן שש את המשפט היסודי של החשבון האינטגרלי, האומר שהאינטגרל המסוים ניתן לחישוב על ידי אינטגרל לא מסוים? מסקנתה די מעניינת - שלפחות כדאי לנסות. המסקנה שאני עצמי הפקתי מן המאמר הזה היא - אם תנסה להסביר לסטודנט בשנה הראשונה את הרעיון כפי שאנה ליזהטוב ממליצה על הסבר לילדים בגיל שש, אולי הוא יבין.
המאמר השני העוסק בחינוך מתמטי נכתב גם הוא בידי אנה ליזהטוב, אבל הרעיון הוא של מושא הערצתה של ליזהטוב, המתמטיקאי הניסויי יסולא פז. מה ליסולא מיודענו ולחינוך מתמטי? תצטרכו לקרוא כדי לגלות.
כמו כן יש שני מאמרים על עקרונות מתמטיים. האחד הוא "אסטרטגיית הקוף", על דרך להוכיח אפשרות ניצחון במשחקים בלי לספק לכך אסטרטגיה מפורשת. המאמר לקוח מן הבלוג המפורסם "לא מדויק" של כתבנו הוותיק גדי אלכסנדרוביץ'. המערכת מנצלת את ההזדמנות הזאת כדי לברך את גדי על לידת בנו בכורו בימים אלו ממש.
מאמר נוסף לקוח גם הוא ממקום אחר - מספר שכתבתי על "מתמטיקה שירה ויופי". הוא דן בחוקי שימור במתמטיקה. כן, יש כאלה לא רק בפיזיקה!
הפעם חוזר גם המדור "השערת החודש", עם השערה מפורסמת מתורת הגרפים.
וכמובן, יש חידות לגדולים. שתיים, הפעם. וגם חידות לקטנים, מן העיתון הרוסי "קוואנט", בתרגומה של אירנה גורליק.
בהנאה!
השערת הכיסוי הכפול במעגלים
רון אהרוני
קומבינטוריקה היא תורת הקבוצות הסופיות. היא דנה במבנים שכל מה שיש בהם הוא איברים ויחסים ביניהם, בדרך כלל מספר סופי של איברים, ואז גם היחסים סופיים, כמובן.
תורת הגרפים היא חלק מן הקומבינטוריקה, חלק שנשמע כאילו הוא אמור להיות טריוויאלי לגמרי: תורת הקבוצות מגודל $latex {2}$. גרף הוא קבוצה $latex {V}$ של נקודות, או בשם הרשמי יותר "קדקודים" ($latex {vertices}$)- מכאן הסימון $latex {V}$, בצירוף אוסף זוגות מתוכן. לזוגות קוראים "צלעות"($latex {edges}$).
מה כבר אפשר לומר על אובייקט כל כך פשוט? הרבה מאוד דברים. הנה למשל משפט מפורסם, שהתגלה לראשונה על ידי מנטל, והתגלה מחדש והוכלל על ידי המתמטיקאי פול טורן שסיפורו הופיע באחד הגליונות הקודמים. אגב - את המשפט הזה גילה טורן בזמן שהיה כלוא במחנה עבודה גרמני במלחמת העולם השנייה .
משפט 1
בגרף על $latex {n}$ קדקודים עם יותר מ-$latex {\frac{n^2}{4}}$ צלעות יש משולש.
האם אתם יכולים להראות שהמספר $latex {\frac{n^2}{4}}$ הוא אכן הטוב ביותר? או אולי אפילו להוכיח את המשפט?
על כך שהפשטות לכאורה שת תורת הגרפי מטעה מלמדת גם העובדה שיש בה הרבה מאוד השערות, שנשמעות פשוטות מאוד, ובכל זאת עומדות בפני מאמציהם של המתמטיקאים לאורך שנים רבות. כאן נספר על אחת מהן: השערת הכיסוי הכפול במעגלים. "מעגל" הוא מה שהוא נשמע - אוסף צלעות שמחבר סדרת קדקודים כל האחד לעוקבו, והאחרון לראשון.
אם בגרף כל צלע משתתפת במעגל, אז יש אוסף מעגלים שמכסה כל צלע בגרף בדיוק פעמיים.
כדי להבין את ההשערה, רשמו תחילה גרף שבו יש צלע שאינה משתתפת במעגל. אחר כך נסו את ההשערה בדוגמאות הבאות:
א. מעגל אחד.
ב. גרף המורכב מ-$latex {4}$ קדקודים, שכולם מחוברים זה לזה.
ג. גרף המורכב מ-$latex {5}$ קדקודים, שכולם מחוברים זה לזה.
ד. גרף המורכב מ-$latex {n}$ קדקודים, שכולם מחוברים זה לזה.
ההשערה הזאת פורסמה לראשונה על ידי סקרש )$latex {George~~Szekeres}$, חבר של פואל ארדש שהיגר מהונגריה לאוסטרליה( ב-$latex {1973}$, והתגלתה מחדש באופן בלתי תלוי על ידי פאול סימור ב-$latex {1980}$. נעשתה בה מעט מאוד התקדמות מאז - אתם מוזמנים לנסות את כוחכם!
הנה היא ההשערה בויקיפדיה: $latex {http://en.wikipedia.org/wiki/Cycle_double_cover}$
איך להסביר לילד בגן את המשפט היסודי של החשבון האינטגרלי
אנה ליזהטוב
1. האם איינשטיין צדק?
נהוג לייחס לאיינשטיין את המשפט הבא: "אם אינך מסוגל להסביר את התוצאה האחרונה שלך לילד בגן, סימן שלא הבנת אותו".
ההומוריסטן המנוח אפריים קישון אמר: "אם אתה רוצה שאנשים יחשבו שאמרה היא חכמה, יחס אותה להוגה ידוע".
אני לא בטוחה אם האמרה של איינשטיין נאמרה על ידו או שמא מישהו השתמש בשמו כדי לומר אותה. היא בוודאי לא נכונה. אף מתמטיקאי לא יצליח להסביר לילד בגן את נושא המחקר העכשווי שלו. קרוב לוודאי שגם לא יצליח להסביר את המשפט האחרון שהוכיח למתמטיקאי שיושב מולו במסדרון. אבל זוהי אמרה מעניינת. אז בואו ננסה להשיב על השאלה: האם אפשר להסביר לילד בגן את עקרונות החשבון הדיפרנציאלי והאינטגרלי?
באחד המאמרים הקודמים סיפרתי לכם איך להסביר לילד בגן את העיקרון החשוב ביותר של החשבון הדיפרנציאלי. זהו העיקרון שעל פיו סברו אנשים עד לפני זמן לא כל כך רב, ביחס, שהעולם שטוח. הסיבה: כשמסתכלים במשהו מקרוב, הוא נראה שטוח. מקרוב, גם עקום נראה ישר. נמלה שהולכת על כדור חושבת שהוא שטוח. הים, אם מתעלמים מן הגלים, נראה לנו שטוח. צריך להיות חכם ולהבין מה קורה כשהשמש שוקעת כדי להבין שזה לא כך. האם אפשר להסביר זאת לילד בגן? אני חושבת שכן. שאלו אותו איך הנמלה יכולה לדעת שהכדור עגול. ייתכן שהוא יבין שבהסתכלות מאוד מקרוב, אין לה דרך לדעת זאת.
היום אני רוצה לספר לכם משהו הרבה יותר אמביציוזי: איך להסביר לילד בגן את המשפט היסודי של החשבון האינטגרלי.
2. מהו המשפט היסודי
המשפט היסודי של החשבון האינטגרלי אומר: האינטגרל על פני קטע של נגזרת של פונקציה הוא הפרש ערכי הפונקציה בשני קצוות הקטע.
למשל, הנגזרת של $latex {f(x)=x^2}$ היא $latex {2x}$, והמשפט אומר: האינטגרל של $latex {2x}$ בין $latex {3}$ ל-$latex {7}$ הוא $latex {7^2-3^2}$, כלומר ההפרש בין ערכי הפונקציה ב-$latex {7}$ וב-$latex {3}$. זה יוצא $latex {40}$, אבל התוצאה אינה מה שמעניין כאן.
אל דאגה, אני לא הולכת לומר זאת לאף ילד בגן של הבן שלי. ההורים יקראו למשטרה. אני מתכוונת לומר משהו שקול. אבל בשביל זה צריך להבין מה המשפט הזה אומר. חכו בסבלנות, ואסביר.
3. טור טלסקופי
בואו אשאל אתכם שאלה מקדימה: כמה הם
$latex \displaystyle (3-1)+(5-3)+(10-5)+(20-10)$
איך מחשבים זאת? האם אתם רואים שאלה הן הקפיצות מ-$latex {1}$ ל-$latex {3}$, ועוד הקפיצה מ-$latex {3}$ ל-$latex {5}$, ועוד קפיצה מ-$latex {5}$ ל-$latex {10}$, ועוד קפיצה מ-$latex {10}$ ל-$latex {20}$? יחד - זוהי הקפיצה מ-$latex {1}$ ל-$latex {20}$. כלומר $latex {19}$. הפרש הפונקציה בשני הקצוות.
הסכום הזה נקרא "טור טלסקופי". "טור" פירושו סכום, ו"טלסקופי" משמעו שהוא מתקפל. כלומר - ה-3 מצטמצם עם ה$latex {(-3)}$, ה-$latex {5}$ עם ה-$latex {(-5)}$ וכו'. נשארים רק האיבר הראשון והאחרון. כלומר - $latex {20-1=19}$.
טור טלסקופי הוא סכום של הפרשים עוקבים.
האם הבנתם זאת? אם כן, הבנתם את המשפט היסודי של החשבון האינטגרלי. זהו המשפט היסודי: סכום של טור טלסקופי הוא ההפרש בין סוף הטור להתחלה שלו.
תכף אסביר לכם מדוע.
4. מה הקשר?
כדי להבין את הקשר צריך להבין מהי נגזרת.
נגזרת היא הפרש.
נכון - אני מגזימה. נגזרת אינה בדיוק הפרש. היא קצב שינוי. נאמר - כמה מטרים אתה מתקדם כל שנייה.
אבל אם תמדדו את הזמן שנייה-שנייה, אז הנגזרת היא כמה נסעת בשנייה. כלומר - הפרש המרחקים כל שנייה. אם כן, בכל זאת הנגזרת היא הפרש. ההפרש בכל יחידת זמן, או באופן כללי, לכל שינוי ביחידה של המשתנה. הכוונה כאן היא שהיחידה קטנה (שנייה זה קטן, לא? המהירות שלך לא אמורה להשתנות הרבה במשך שנייה. אתה נוסע בקצב קבוע - בגרף ישר. אמרנו: מקרוב הכל נראה ישר)
OK, אז נגזרת היא הפרש ערכי פונקציה. נאמר, באיזה מרחק תמצא אחרי שנייה, פחות המרחק שהגעת אליו עכשיו.
ואינטגרל? אינטגרל הוא סכום. לכן הסימן שלו, $latex {\int}$. זהו ה-$latex {S}$ של "$latex {Schum}$", או של "$latex {Sum}$". סכום של מה? של ערכי הפונקציה. למתקדמים - של ערכי הפונקציה כפול התזוזה במשתנה. אבל כמו במקרה של הנגזרת, בואו נניח שהשינויים במשתנה הם יחידה אחת בכל צעד. נאמר, שנייה אחת.
אם כן, מהו האינטגרל של נגזרת? זהו סכום ההפרשים.
וסכום ההפרשים הוא סכום של טור טלסקופי, כלומר הפרש הפונקציה בשני הקצוות.
5. האם אפשר להסביר זאת לילד בגן?
משהו מזה גם ילד בגן יכול להבין: מה זה טור טלסקופי.
בואו ניגש לילד בגן, ונשאל אותו. היו לך 3 סמיילים. ביום הראשון הגננת נתנה לך שני סמיילים. כמה יש לך יותר מאתמול?
ביום השני היא נתנה לך סמיילי אחד. כמה יש לך יותר מאשר ביום הקודם? וכמה יש לך יותר מאשר לפני יומיים? ביום השלישי היא נתנה לך 5 סמיילים. כמה סמיילים נוספו לך מאז תחילת שבוע?
ולבסוף, שאלו אותו: כמה סמיילים נוספו לך לאורך כל השבוע?
התשובה - השינוי הכולל הוא סכום כל השינויים.
6. למה חשוב לדעת זאת
מי שהבין את העיקרון הזה, יבין היטב יותר את המשפטים המתקדמים יותר של החשבון האינטגרלי, כמו משפט גאוס, גרין וסטוקס. כולם אומרים אותו דבר - אם מסכמים דברים שמצטמצמים בתוך התחום, תקבלו את ההפרשים על השפה. למשל, אם תסכמו מערבולות בתוך תחום במישור. שימו הרבה מערבולות קטנות זו ליד זו, במישור, כולן נגד כיוון השעון. בתוך התחום כל מערבולת תתבטל על ידי המערבולות הסמוכות לה. מה שלא יבתטל הוא המערבולות על השפה. מתקבל - האינטגרל של המערבולות בפנים הוא ה"מערבולת הגדולה" לאורך השפה - כמה תנועה יש לאורך השפה, נגד כיוון השעון. מה שאמרנו כרגע נקרא "משפט סטוקס". פיזיקאים מבינים אותו היטב, כי הם ממחישים אותו לעצמם בדמות של מערבולות ושל סיכום של מערבולות.
7. האם כדאי להסביר זאת לילד בגן?
"אפשר להסביר" ו"כדאי להסביר" הם שני דברים שונים. האם כדאי להסביר?
התשובה היא: טור טלסקופי כדאי להסביר. כאמור, בצורה שהילד יבין. אבל הרבה יותר חשוב מזה: אפשר להסביר זאת לתלמידי אוניברסיטה, וגם לתלמידי תיכון. חשוב להבין שזה כל מה שיש במשפט היסודי. אני חושב שזה בעצם מה שאיינשטיין התכוון לו: הסבר זאת לעצמך בצורה שתבין. כי להבין את המשפט באמת פירושו להבין את העיקרון שמאחוריו, לא איזו קליפה חיצונית שלו.
איך יודעים שכדאי? לכו בקשו מתלמיד בשנה שלישית לספר לכם את ההוכחה למשפט. קרוב לוודאי שלא יידע. כי הוא לא הבין. אם תספרו לו את העיקרון, של הטור הטלסקופי, הוא בוודאי יבין ויזכור.
צ'ומפ צ'ומפ
גדי אלכסנדרוביץ
מאמר זה עוסק בהוכחות לא קונסטרוקטיביות. הדוגמה שנביא במאמר זה הינו המשחק מטופש ותמים ביותר בשם Chomp.
המשחק הולך כך: לוח המשחק הוא מלבן הבנוי מריבועים (ממדי המלבן יכולים להשתנות ממשחק למשחק – זה מה שלכאורה מוסיף אתגר). ישנם שני שחקנים המשחקים לסירוגין. בכל סיבוב אחד השחקנים בוחר אחת מהמשבצות, ומסיר מהלוח אותה ואת כל המשבצות שנמצאות במלבן שהיא הפינה השמאלית התחתונה שלו – במילים אחרות, כל משבצת שנמצאת לימינה או מעליה.
המשבצת השמאלית התחתונה ביותר בלוח היא "מורעלת" – מי שלוקח אותה, הפסיד. לכן, מטרת המשחק היא לגרום ליריב לקחת אותה. בכך המשחק מזכיר מעט את המשחק "נים", שגם בו המטרה היא לא להיות זה שלוקח את האובייקט האחרון.
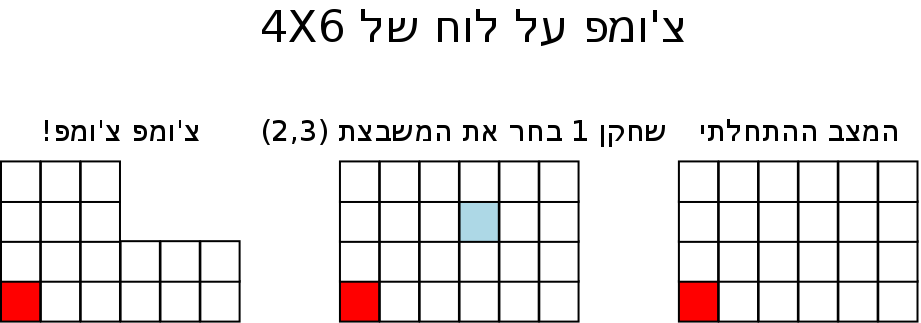
מה שהופך את המשחק הזה למעניין היא העובדה שאפשר להוכיח (בצורה פשוטה ביותר) שהשחקן שפותח תמיד יכול לנצח במשחק (בכל לוח, ובלי תלות בשאלה מה עושה השחקן השני), אבל ההוכחה הזו אינה קונסטרוקטיבית; היא אינה מצביעה כלל על הדרך שבה השחקן הזה צריך לשחק כדי לנצח.
ההוכחה עצמה היא טריוויאלית, אבל היא מתבססת על משפט ידוע ומוכר מתורת המשחקים – משפט צרמלו. המשפט מוצג במספר וריאציות (שכולן די שונות מהנוסח המקורי של צרמלו עצמו), ואציג כאן אחת מהפשוטות שבהן, אשר ממנה נובע שב-Chomp אחד משני השחקנים בהכרח מסוגל לנצח בלי תלות במה שעושה היריב.
לפני כן כדאי לומר מילה או שתיים על המושג המתמטי של "משחק". בהגדרה מקושקשת משהו אפשר לומר ש"משחק" הוא כל סיטואציה בה משתתף אחד או יותר נוקט בסדרה של החלטות כדי להגיע לתוצאה שהיא אופטימלית בעיניו. מילת המפתח כאן היא "החלטה" – אם אין החלטות, המשחק די חסר טעם.
משחקים לשחקן יחיד לא חסרים, ושלוש הדוגמאות המוכרות של ימינו, באדיבותה של חברת מיקרוסופט, הן סוליטייר, פריסל ושולה המוקשים. עם זאת, העניין האמיתי מתעורר כאשר יש שני שחקנים או יותר – במצב זה, השחקן אינו תלוי רק בעצמו כדי לקבוע את תוצאת המשחק; הוא צריך להביא בחשבון גם את מה שהשחקנים האחרים יעשו.
כאשר רוצים לתאר משחק בצורה מתמטית, ישנן מספר דרכים לעשות זאת. גישה אחת, שנכנסת אל תוך המכניקות הפנימיות של המשחק, מתארת אותו בתור עץ מכוון שכל צומת בו מייצג סיטואציה אפשרית כלשהי במשחק (למשל, השורש שלו מייצג את המצב ההתחלתי של המשחק, והעלים את סוף המשחק) ויש קשת מצומת אחד לצומת שני אם בחירות השחקנים במצב שמגולם באב יכולות להוביל למצב שמגולם בבן (יש לשים לב כי גם לאותו מצב בלוח עשויים להיות כמה וכמה צמתים שונים בעץ, שכן צומת בעץ מייצג לא רק את המצב אלא גם את הדרך שבה הגענו אליו).
באמצעות דרך הייצוג הזו קל להוכיח את הגרסה שלנו של משפט צרמלו, שגורסת כי במשחק סופי (כזה שתמיד נגמר) לשני שחקנים שמשחקים לסירוגין, עם ידיעה גמורה, שבו התוצאות האפשריות היחידות הן ניצחון לאחד משני השחקנים (נקרא להם מעכשיו "הלבן" ו"השחור", כמו בשחמט, כדי לפשט, כאשר "הלבן" הוא זה שמתחיל), בהכרח אחד מהשחקנים מסוגל לכפות ניצחון בלי תלות במעשי השני.
המונח הבעייתי היחיד בניסוח המשפט הוא "ידיעה גמורה". משמעותו היא שבכל סיבוב השחקנים יודעים בדיוק היכן בעץ המשחק הם נמצאים, ואילו פעולות עליהם לנקוט כדי לעבור לצומת הבא. בפועל פירוש הדבר הוא שבמשחק אין מידע מוסתר (למשל, בטקטיקו מוסתרים מכל שחקן הכלים של השחקן השני, ובשולה המוקשים יש משבצות שלא ניתן לדעת את תוכנן וחייבים לנחש), ואין מימד של אקראיות (למשל, במונופול השחקנים מתקדמים על ידי הטלת קובייה). אפשר לסלק את האקראיות ולהישאר רק עם חוסר ודאות על ידי כך שחושבים על סדרת האקראיות כאילו כבר "נקבעה מראש" והיא פשוט לא ידועה, אך לא ניכנס לזה.
הדרך להוכיח שאחד משני השחקנים יכול לכפות ניצחון היא זו: ראשית, כל עלה בעץ מסמל ניצחון במשחק של אחד השחקנים (כי המשחק חייב להסתיים בניצחון). אם כן, נסמן ב-1 את העלים שמסמלים ניצחון של השחקן הלבן, וב-0 עלים שמסמלים ניצחון של השחור. כעת, באופן אינדוקטיבי, נסמן גם את שאר הצמתים בעץ במספרים: בהינתן צומת שמסמל סיטואציה במשחק בה תורו של השחקן הלבן, הסימון שבצומת יהיה פונקצית "או" של כל הבנים של הצומת (כלומר, 1 אם אחד מהם הוא 1, ו-0 אם כולם 0), ובהינתן צומת שמסמל את תורו של השחקן השחור, הפונקציה תהיה "וגם" (1 רק אם כולם 1, 0 אם אחד מהם 0).
בצורה הזו מסומן כל העץ, ובפרט השורש. אם השורש מסומן ב-1, הלבן יכול לכפות ניצחון. אם הוא מסומן ב-0, השחור יכול לכפות ניצחון.
למה? כי נניח שהשורש מסומן ב-1, וזה צומת שמסמל מהלך של הלבן (כי הלבן מתחיל). פירוש הדבר שלפחות אחד מבניו הוא 1. הוא יבחר במהלך במשחק שמביא אותו לבן הזה. עכשיו תור השחור. הוא בצומת שמסומן 1, ולכן כל בניו של הצומת הם 1, ולכן בלי קשר לשאלה מה יבחר לעשות השחקן השחור, הוא עדיין יגיע לצומת של 1. שוב תור השחקן הלבן, והוא שוב ימשיך לצומת שמסומן ב-1 וכן הלאה. האינוריאנטה נשמרת; המשחק תמיד נמצא בצומת שמסומן ב-1. מכיוון שהמשחק סופי, מתישהו יגיע הטיול בעץ לעלה, ובשל האינוריאנטה העלה יהיה מסומן ב-1 – כלומר, הלבן ניצח, בלי תלות במה שעשה השחור. החשיבות היחידה הייתה לבחירות שהלבן ביצע במהלך כל הטיול בעץ. לסדרה הכוללת של הבחירות שהיה עליו לבצע ("אם השחור ביצע את המהלך הזה, עשה כך וכך. אם השחור עשה דווקא את זה, אז עשה כך וכך וכך") קוראים אסטרטגיה.
אם השורש הוא 0, ההוכחה דומה; נסו לחשוב על הפרטים בעצמכם.
וכעת חזרה לצ'ומפ, כשאנחנו משוכנעים שאו הלבן יכול לכפות ניצחון, או השחור. אני רוצה להוכיח שבהכרח הלבן יכול לכפות ניצחון. ההוכחה היא כדלהלן:
נניח בשלילה שדווקא השחור יכול לכפות ניצחון, כלומר יש לו אסטרטגיה שמבטיחה ניצחון לכל פעולה של הלבן. בפרט, יש לו תגובה שתבטיח ניצחון למשחק של הלבן שבו הצעד הראשון הוא בחירת המשבצת הימנית העליונה בלוח.
כעת, אנחנו לא יודעים מה הצעד של השחור יהיה, ומה הוא המשך האסטרטגיה שלו, אבל אנחנו יודעים בודאות שהלבן יכול "לגנוב" אותם. איך? נניח לרגע שהמהלך של השחור מתחיל בבחירת המשבצת בקוארדינטה (2,3), ומכאן והלאה תגובה הולמת לכל מהלך של הלבן. אז הלבן יכול להתחיל את המשחק בכך שיבחר את הקוארדינטה (2,3), ומכאן והלאה יפעל על פי האסטרטגיה המנצחת של השחור.
מקור הכוח של הלבן הוא שבחירת הקוארדינטה (1,1) לא באמת משפיע על כלום. זה "מהלך סרק" – לא משנה איזה מהלך השחור יבצע כעת, הלוח בסיום המהלך הזה יהיה זהה ללוח שהלבן יכל להגיע אליו על ידי ביצוע אותו מהלך של השחור כבר בסיבוב הראשון.
אם, למשל, הלבן היה בוחר את (2,2) בסיבוב הראשון, התעלול לא היה פועל: השחור היה מסוגל לבחור משבצת כלשהי כך שהלוח אחרי בחירתה היה במצב שאליו הלבן לא מסוגל להגיע בסיבוב הראשון – נסו לחשוב על מהלך שכזה.
אם כן, הפרכנו את הטענה שלשחור יש אסטרטגיה מנצחת, ולכן על פי משפט צרמלו זהו הלבן שיש לו אסטרטגיה מנצחת, וגמרנו. רק מה? לא אמרנו שום דבר על מהי האסטרטגיה הזו – אפילו את המהלך הראשון שלה איננו יודעים. המשחק מכור מראש למרות שאין לנו מושג איך.
רק הערה כללית לסיום: משפט צרמלו שהוצג כאן תקף גם למשחקים עם תוצאת תיקו (ההכללה מיידית – תנו ערך 1 לניצחון של הלבן, 0 לתיקו ומינוס 1 לניצחון של השחור, ובחרו בצמתים פונקציות של "מקסימום" ללבן ו"מינימום" לשחור), ולכן תקף לשחמט ולדמקה. בכל הנוגע לשחמט, איש אינו יודע איזו מבין שלוש האפשרויות נכונה (האם הלבן יכול לכפות ניצחון, השחור יכול לכפות ניצחון, או כל אחד יכול לכפות תיקו) ומכיוון שעץ המשחק של שחמט הוא עצום בגודלו, גם לא סביר שפתרון יתגלה כל כך מהר, אבל דמקה כבר "פוצחה" בצורה הזו לא מזמן (או לפחות כך נטען) והוכח שכל שחקן בה מסוגל לכפות תיקו.
אני מודה שאיני יודע אם התגלית הזו משמחת או מדכאת אותי.
מאמר זה פורסם במקור בבלוג "לא מדויק"
חוקי שימור
רון אהרוני
תחתוך לי את הפיצה לארבע חתיכות. אני לא מספיק רעב לשש חתיכות.
(יוֹגי בֶּרָה, שחקן בייסבול)
אני רוצה להציע לכם משימה. מי שישלים אותה יקבל פרס של 1000 שקלים. הנה המשימה: צאו מן המספר 1, ובצעו סדרה של צעדים שבכל אחד מהם אתם מוסיפים או מחסירים מכפלה של שני מספרים עוקבים. המטרה – להגיע. למספר 10. למשל, בצעד הראשון אתם יכולים להוסיף 6, שהוא מכפלת 2 ב-3. אתם מגיעים ל-7. בצעד הבא אתם יכולים להוסיף 56, שהוא $latex { 7*8 }$, ולהגיע ל-63. עכשיו מותר לכם להחסיר, נאמר, 20 (שהוא $latex { 4*5 }$ ). האם תצליחו להגיע ל-10?
התשובה היא "לא", כלומר לא סיכנתי את כספי. הסיבה: מכפלת שני מספרים עוקבים היא תמיד זוגית. לכן בכל צעד אתם מוסיפים או מחסירים מספר זוגי. מכיוון שיצאתם ממספר אי זוגי, 1, תקבלו בכל צעד מספר אי זוגי. ו-10 הוא זוגי.
שאלה: האם אפשר להגיע במשחק הזה לכל מספר איזוגי?
מה שיש לנו כאן הוא "חוק של שימור". איזושהי תכונה של המערכת נשארת קבועה לאורך כל הדרך. "חוק שימור" אומר שדבר מה – כמות, גודל או יחס – נשמרים, גם כאשר גורמים אחרים בתמונה משתנים. למשל, אם תזיז את הכיסא שעליו אתה יושב ישתנה מקומו, אבל לא ישתנו היחסים בין חלקיו והוא יישאר כיסא. בזכות חוקי שימור פשוטים מסוג זה אפשר להתייחס לעולם במושגים קבועים. יש חוקי שימור מופשטים יותר, כמו למשל שימור המספר: אם תיקח 4 אבנים ותסדר אותן בשורה, ואחר כך תזיז אותן ותסדר אותן בריבוע, לא ישתנה מספרן. עוד יותר מופשט הוא שימור כמות רציפה. בניסוי מפורסם העביר הפסיכולוג השוויצארי ז'ן פיאז'ה (Jean Piaget, 1896-1980) נוזל מכלי רחב לכלי צר. מובן שבכלי הצר הגיע הנוזל לגובה רב יותר, וכשילדים בני ארבע או אף חמש נשאלו אם כמות הנוזל השתנתה, הם השיבו שכן, עכשיו יש יותר, אף כי הנוזל הועבר מן הכלי האחד לאחר לנגד עיניהם.
המוכרים ביותר הם חוקי השימור של הפיזיקה: שימור המסה, האנרגיה, התֶּנע (מכפלת המסה במהירות), התנע הזוויתי. בעזרתם אפשר לפתור באופן אלגנטי הרבה בעיות פיזיקליות. פחות ידועה העובדה שגם במתמטיקה משתמשים בחוקי שימור. השוני הוא בכך שבמתמטיקה החוקים בדרך כלל סמויים יותר, משום שהגודל הנשמר אינו שקוף כל כך. הקושי לגלות את הגודל שנשמר הוא אחד מסודות יופיים של חוקי השימור המתמטיים.
חוק שימור שמוכר לכול, אף כי בדרך כלל אין חושבים עליו במונחים של שימור, הוא כללי ההרחבה והצמצום של שברים. קחו עוגה, וחלקו אותה לשני חצאים. בניגוד לדעתו של יוֹגי בֶּרָה בציטוט לעיל, כמות העוגה הכוללת השתמרה ובידינו עדיין עוגה אחת. פירוש הדבר הוא ש-1 (עוגה אחת) שווה ל-2 חצאים, או בסימון מספרי – $latex { 1 = \frac{2}{2} }$. בדומה, אם תיקחו $latex { \frac{2}{3} }$ עוגה ותחלקו כל אחד משני השלישים ל-5 חלקים, לא תשתנה כמות העוגה. אבל עתה כל שליש הפך ל-5 חלקים, שכל אחד מהם הוא $latex { \frac{1}{15} }$ מן העוגה. כלומר, בשני השלישים יחד יש 10 חלקי 15, וכך קיבלנו: $latex { \frac{2}{3} = \frac{10}{15} }$.
במאמר הזה אני רוצה לספר לכם על מישהו שהרוויח כסף מחוק שימור. הוא הציע משחק דומה מאוד למשחק שהצעתי בתחילת המאמר, רק מעט יותר מתוחכם. ומכיוון שהיה לו גם חוש עסקי, הוא הצליח להתעשר.
איך להתעשר מחוק שימור
סם לויד (1911-Sam Lloyd, 1841) האמריקאי היה מיוצרי החידות הגאוניים של כל הזמנים. הוא חיבר חידות שחמט בצד חידות מתמטיות, היה קוסם חובב, פיתום (וֶנטרילוֹקווִיסְט, כלומר דובר מן הבטן) מקצועי, ושילב את אמנות הפיתום בהופעות הקסמים שלו. בנו היה "קורא" את מחשבותיו, כשלמעשה הוא עצמו היה מדבר מפי בנו. בשנת 1878 חיבר (יש הטוענים – שאל ממקור אחר) את חידתו המפורסמת ביותר, "משחק ה-15". במקור אין זו חידה אלא משחק, הנמכר עד עצם היום הזה. הוא עשוי מריבוע בן 16 משבצות, שבהן 15 לוחיות שעליהן רשומים המספרים מ-1 עד 15, בעוד אחת המשבצות נשארת ריקה. את הלוחיות ניתן להזיז אל המשבצת הריקה, אם הן סמוכות לה, כלומר נמצאות לצידה, מעליה או מתחתיה. הדרך הרגילה לשחק את המשחק היא לסדר את הלוחיות בסדר מִקרי, ולנסות להגיע למצב שבצד ימין של האיור שלהלן, על ידי סידרת מסעים חוקיים.
כדי להגדיל את המכירות, הציע לויד פרס בסך 1000$ (סכום נכבד באותם ימים, אבל מספיק צנוע כדי לא לעורר חשד הטעיה) למי שיבצע את המשימה הבאה: יחליף, על ידי סידרת מסעים חוקיים, את מקומם של ה-14 וה-15.
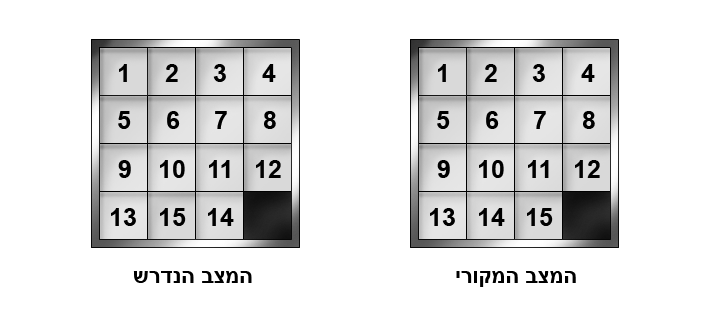
אפילו לויד עצמו לא שיער לאן הדבר יוליך. המהומה שהתחוללה עלתה אף על שיגעון הקובייה ההונגרית שהשתלט על העולם כמאה שנים אחר כך. אנשים זנחו את עבודתם וסבבו ברחובות כשהמשחק בידיהם. בצרפת נחקק חוק האוסר להחזיק במשחק בעבודה. לויד התעשר, וידע היטב שאינו מסכן ולו סנט אחד, משום שהמשימה היא בלתי אפשרית. באותם ימים לא התפשטו השמועות באותה מהירות כמו בעידן האינטרנט, ומסיבה כלשהי אף עיתונאי לא טרח לראיין מתמטיקאים, וכך עבר זמן רב עד שאנשים למדו על אי האפשרות של ביצוע המטלה.
אי האפשרות הזה נובע מחוק של שימור. יש פרמטר (מספר) שנשמר קבוע לאורך כל המשחק, משום שמסע חוקי במשחק אינו משנה אותו. פירוש הדבר הוא שבכל המצבים שאפשר להגיע אליהם בעזרת מסעים חוקיים הפרמטר הזה מקבל אותו ערך, הלא הוא הערך ההתחלתי, זה שהיה במצב המוצא. אם נראה שבמצב שאליו חותרים, שבו ה-14 וה-15 מתחלפים, הערך של הפרמטר שונה מן הערך ההתחלתי, כי אז ברור שאין סידרת מסעים חוקיים שמובילה למצב זה.
הפרמטר המדובר הוא הזוגיות של מספר חילופי הסדר של הלוחיות (אם רוצים שהפרמטר יהיה מספר, נגדיר אותו כ-0 אם מספר חילופי הסדר זוגי, וכ-1 אם לא). כדי להבין את המושג "חילופי סדר" נדגים אותו במקרה של סידור המספרים 1,2,3,4. כשהם כתובים כך, המספרים מופיעים על פי סידרם, ואין בהם חילופי סדר. מספר חילופי הסדר שלהם הוא על כן 0. כשהם כתובים בסדר 2,1,3,4 יש בהם חילוף סדר אחד: הזוג (1,2) מופיע בסדר הפוך, משום ש-2 קודם ל-1, שלא כמו בסדר הרגיל. בסידרה 3,2,4,1 יש 4 חילופי סדר, כלומר 4 זוגות של מספרים המופיעים בסדר הפוך מן הרגיל: אלה הם הזוגות (1,2) (משום ש-1 מופיע בסידרה מימין ל-2, כלומר אחריו), (1,3), (2,3) ו-(1,4).
"חילופי סדר" מוגדרים כאשר המספרים מסודרים בשורה. במשחק ה-15 הלוחיות מסודרות בריבוע, ולא בשורה, לכן לא ברור איך לספור בהן את חילופי הסדר. כדי להגדיר "חילופי סדר" אין ברירה, אלא לפרוש אותן בשורה, וזאת אפשר לעשות בדרכים רבות. אנו נבחר בסדר הבא:
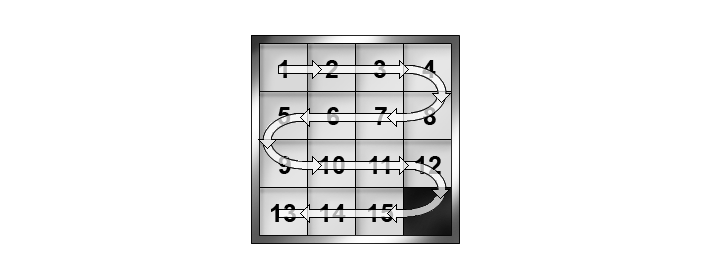
פורשים את המשבצות בלוח לסידרה, על פי הסדר של החץ המעוקל.
כפי שאפשר לראות באיור, הסידור המקורי יהפוך לסידרה 1,2,3,4,8,7,6,5,9,10,11,12,15,14,13. כמה חילופי סדר יש כאן? התבוננות קצרה תראה שחילופי סדר קיימים רק בין מספרים שמופיעים בריבוע בשורות השנייה והרביעית, כלומר רק בתוך הסדרות 8,7,6,5 ו-15,14,13. בסידרה הראשונה כל 6 הזוגות (5,6),(5,7),(5,8),(6,7),(6,8),(7,8) מופיעים בסדר הלא נכון. בסידרה השנייה כל 3 הזוגות (13,14),(13,15),(14,15) מופיעים בסדר הלא נכון. יחד יש כאן אפוא 9 חילופי סדר.
מהו מספר חילופי הסדר במצב הרצוי? הסידרה המתאימה שם, כשהיא פְּרוּשָׂה על פי הסדר שמכתיב החץ המתפתל, היא: 1,2,3,4,8,7,6,5,9,10,11,12,14,15,13. זוהי סידרה זהה כמעט לסידרה של המצב ההתחלתי, פרט לכך שה-15 וה-14 נמצאים עתה בסדר הנכון, בעוד שבמצב ההתחלתי הם היו הפוכים. כלומר יש כאן חילוף סדר אחד פחות, שפירושו 8 חילופי סדר.
מספר חילופי הסדר במקור, שהוא כאמור 9, הוא אי זוגי. אנו נראה שמסע מותר אינו משנה את הזוגיות של מספר חילופי הסדר. לכן לאורך כל המשחק יישאר מספר חילופי הסדר אי זוגי. מכיוון שמספר חילופי הסדר במצב המבוקש הוא 8, שהוא מספר זוגי, ינבע מכך שאי אפשר להגיע אל המצב המבוקש.
מה עושה מסע חוקי למספר חילופי הסדר? יש שני סוגי מסעים – אופקי ואנכי. מסע אופקי אינו משנה כלל את סדר הלוחיות, ולכן אינו משנה גם את מספר חילופי הסדר. מסע אנכי עשוי לשנות את מספר חילופי הסדר. ובכל זאת, הזוגיות של מספר חילופי הסדר לא תשתנה. הסיבה היא שמסע אנכי מחליף את סדרה של הלוחית שזזה עם מספר זוגי של לוחיות אחרות. למשל, המסע הבא אינו מחליף סדר כלל:

מסע זה אינו משנה את הסדר של המספרים: בסדר המותווה על ידי החץ המתפתל הופיעה לוחית ה-12 לפני לוחיות ה-13, 14, 15 לפני המסע, וכך הוא גם אחרי המסע.
המסע שבציור הבא משנה את מספר החלפות הסדר עם 4 לוחיות. הוא מוסיף 3 חילופי סדר, וגורע אחד. חילופי הסדר שנוספים הם עם 6, 7, ו-8, ואילו חילוף הסדר שנגרע הוא עם 1: לפני המסע 5 לא היה בסדר הנכון עם 1 (5 גדול מ-1, ובא לפניו), ואילו אחרי המסע חילוף הסדר הזה נעלם, כלומר 5 ו-1 נמצאים בסדרם הנכון, 1 לפני 5. בסך הכול נוספים 3-1, כלומר 2 חילופי סדר (למען הבהירות, סומנו בריבוע רק המספרים הרלבנטיים).
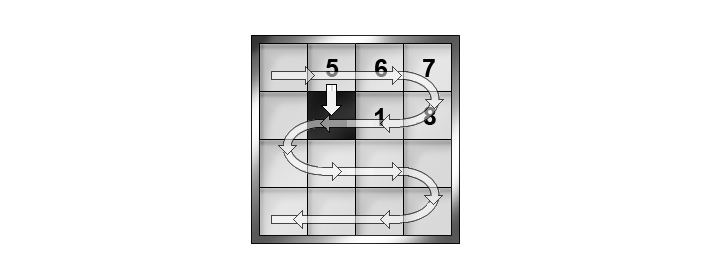
מסע זה משנה את מצבו של 5 ביחס ל-4 לוחיות. הוא מוסיף 3 חילופי סדר, עם 6, 7 ו-8, ולעומת זאת מחסיר חילוף סדר אחד, עם 1. בסך הכול מתווספים 2=3-1 חילופי סדר. פירוש הדבר הוא שהזוגיות של מספר חילופי הסדר לא השתנתה.
הוספה או גריעה של חילוף סדר אחד משנה את הזוגיות של מספר חילופי הסדר. לכן ארבעה שינויים בחילופי סדר פירושם חציית נהר הזוגיות של מספר חילופי הסדר 4 פעמים, כאשר "חציית הנהר" היא החלפת זוגיות. כאשר חוצים נהר 4 פעמים, חוזרים לאותו צד. לכן 4 שינויים בחילופי הסדר אינם משנים את הזוגיות של מספר חילופי הסדר.
העובדה שבשתי הדוגמאות שנתנו שוּנָה מספר זוגי של חילופי סדר לא הייתה מקרית. תמיד נוסף או נגרע מספר זוגי של חילופי סדר. הסיבה היא שהלוחיות שאיתן שונה הסדר נמצאות או מימין ללוחית שזזה (כמו בדוגמה של ה-5 שירד משבצת), או משמאל לה, בשתי שורות – שורת המוצא של הלוחית שזזה, והשורה שאליה היא עוברת. לכן הלוחיות שאיתן שונה הסדר מסודרות בזוגות: בדוגמה שלנו אלה הם הזוגות 6 ו-1, שנמצאים זה מעל זה, ו-7 ו-8, שנמצאים זה מעל זה. מכיוון שהן מסודרות בזוגות, מספר הלוחיות האלה הוא זוגי.
יש כאן אם כן חוק שימור – שימור של זוגיות מספר חילופי הסדר. בלשון של "עקרון חציית הנהר" שבו פגשנו בפרק על ההתקה, חוק השימור הזה אומר שאין לנו בכלל סירה לחצות את הנהר. אנחנו נידונים להישאר תמיד באותו צד – הצד ה"אי זוגי". לכן לא נוכל לחצות את הנהר כדי להגיע למצב המבוקש באתגר שהציב סם לויד.
שימור האמת הפנימית
בטרגדיות יווניות רבות מנסה הגיבור להימלט מגורלו, רק כדי להיווכח שלמעשה רדף אחריו. הידועה בין הטרגדיות שזהו מהלכן היא "אדיפוס המלך" של סופוקלס. אדיפוס, נסיך העיר פילוֹס, שומע נבואה שיהרוג את אביו ויישא לאישה את אימו. מבועת, הוא מחליט להימלט מן העיר. במסעותיו הוא פוגש בצומת דרכים אדם והורג אותו בתגרה. לאחר מכן הוא מגיע לעיר תֶבַּי, ובשער העיר נודע לו על מפלצת, הספינקס, ראשה ראש אדם וגופה גוף חיה, שגובה מחיר דמים מתושבי העיר. קללתה של המפלצת לא תסור עד שתיפתר חידה שהיא מציגה. אדיפוס פותר את החידה, וכאות תודה משיאים אותו בני העיר ליוֹקַסְטָה, המלכה האלמנה. כעבור שנים, בעקבות מגיפה שמתחוללת בתבי, וטענותיהם של חוזים שבו האשָם, מתגלה לאדיפוס האמת: למעשה, הוא אסופי; יוקסטה אימו מסרה אותו לידי רועה שיגדלו, לאחר ששמעה מפי חוזים בדיוק אותה נבואה ששמע גם הוא; והאדם שהרג בצומת הדרכים היה אביו הביולוגי. הנבואה, הוברר לו לחרדתו, התקיימה בדיוק אכזרי.
בני ימינו יפרשו את הגורל כמסמל כוחות פנימיים. המסר בטרגדיה הוא שהכוחות האלה חזקים ממך, ושאינך יכול להתכחש לפנימיותך. נדמה לך שאתה שולט בחייך, כאשר למעשה מאווייך העמוקים מכוונים אותך יותר מאשר החשיבה המודעת. המשורר הגדול איש אלכסנדריה קונסטנטין קוואפיס (Kawafis) היה הלניסט (מעריץ תרבות יוון העתיקה) מושבע, והמסר הזה מוטמע בשיריו. במיוחד, באחד משיריו המפורסמים ביותר, "העיר", שהוא שיר של "שימור האמת הפנימית". חוקי שימור אומרים שבעוד הכול משתנה מסביב, משהו מהותי הנמצא בעין הסערה נשאר קבוע. המסר ב"העיר" הוא שהחוץ יכול להשתנות, אבל מהותך הפנימית תישאר כפי שהיא. קוואפיס חי בין השנים 1863 ו-1933, הרחק ממרכזי הספרות האירופאיים, היה הומוסקסואל, התפרנס מעבודה פקידותית, כתב יוונית, והתפרסם בעיקר לאחר מותו. אבל דומה ש"העיר" מאפשר הצצה לתוך נפשו יותר מאשר יוכלו לסכם כל העובדות החיצוניות האלה. השיר מובא כאן בראשון מבין שני תרגומים שעשה לו יורם ברונובסקי.
אָמַרְתָּ: "אֵלֵךְ לְאֶרֶץ אַחֶרֶת, אַפְלִיג בְּיָם אַחֵר,
תִּמָּצֵא לִי עִיר שׁוֹנָה, טוֹבָה מִזּוֹ פִּי כַּמָּה
כָּאן כָּל שֶׁאֶעֱשֶׂה מוּעָד לְכִשָּׁלוֹן
כָּאן נָמֵק לִבִּי כְּמוֹ בְּתוֹךְ הַקֶּבֶר.
כְּלוּם לֹא תָּקוּם בִּי הָרוּחַ לְהִתְנַעֵר מִן הָרִפְיוֹן?
בְּכָל אֲשֶׁר אַפְנֶה אֶת מַבָּטִי אֲנִי רוֹאֶה
רַק אֶת הֶחֳרָבוֹת הַמַּשְׁחִירוֹת שֶׁל חַיַּי –
כָּאן חָיִיתִי כָּל כָּךְ הַרְבֵּה שָׁנִים, כָּאן לַהֶבֶל זָרִיתִי יָמַי".
"לֹא תִּמְצָא עָרִים שׁוֹנוֹת, לֹא תַּפְלִיג בְּיָם אַחֵר –
הָעִיר תֵּלֵךְ בְּעִקְבוֹתֶיךָ, תָּמִיד תִּסֹּב בְּאוֹתָם הָרְחוֹבוֹת
הַזִּקְנָה תַּשִּׂיג אוֹתְךָ בְּתוֹךְ אוֹתָם הָרְבָעִים
וּבְאוֹתָם בָּתִּים יַלְבִּין שְׂעַר רֹאשְׁךָ.
תָּמִיד תִּמָּצֵא לְךָ רַק זוֹ הָעִיר. אַל תְּקַוֶּה לַשָּׁוְא
אֵין סְפִינָה תּוֹלִיכְךָ מִכָּאן, אֵין דֶּרֶךְ.
כִּי כַּאֲשֶׁר לַהֶבֶל זָרִיתָ אֶת יָמֶיךָ
זָרִיתָ אוֹתָם עַל פְּנֵי הָאֲדָמָה כֻּלָּהּ, עַל פְּנֵי כָּל הַיָּמִים".
("העיר", קונסטנטין קוואפיס, תרגום – יורם ברונובסקי)
נדמה לו לאדם, אומר השיר הזה, שבעיותיו מגיעות מן החוץ. למעשה אישיותו משמעותית הרבה יותר. אינני חושב שיש דבר חשוב יותר שאדם יכול ללמוד בחייו. "דע את עצמך", אמרו היוונים, ואילו השיר הזה אומר דבר מה ראשוני עוד יותר: שיש מה לדעת. אישיותו של אדם אינה קצף על פני המים.
מה שהופך את השיר הזה ליפה כל כך אינו התוכן, שכאמור אינו חדש, אלא דרך האמירה. למרבה הפרדוקסליות, את הרעיון שהדברים החשובים הם בתוכך אומר השיר בדיוק בלשון ההפוכה – דרך החוץ. לא "אתה תישאר אתה", אלא "הרחובות יישארו אותם רחובות"; לא "אינך יכול לברוח מעצמך", אלא "העיר תלך בעקבותיך". לא "אין זה משנה היכן תהיה", אלא "באותם בתים ילבין שער ראשך".

קונסטנטין קוואפיס, 1933-1863.
(המאמר הוא פרק מתוך "מתמטיקה, שירה ויופי", ספר של רון אהרוני, הוצאת הקיבוץ המאוחד 2008.)
מהפכה בשיטת הבחינות בטכניון
אנה ליזהטוב
תושבי הקומות התחתונות של בניין אמאדו, שבו שוכנת הפקולטה למתמטיקה בטכניון, הופתעו בשבועות האחרונים מן הריחות העולים מאחת המעבדות שהקים שם ראש המחלקה למתמטיקה ניסויית, ד"ר יסולא פז. אין זה ריח בלתי נעים. להפך, על רקע הריח הרגיל של דפי הצילום ושל היובש המתמטי, סבורים יושבי הבניין שיש בו משום ריענון. ובכל זאת, קשה להם להבין כיצד מגיע לפקולטה למתמטיקה ריח של חציר וקש. ועוד פחות מובנים הם הקולות הבוקעים מן המעבדה. רבים מוכנים להישבע שזהו ציוץ של עכברים. מה לעכברים ולמתמטיקה?
בימים אלו נפתרה החידה. ד"ר יסולא פז, מנהל המעבדה, יצא אחרי זמן ארוך של הסתגרות וגילה את סודו. הוא גידל במעבדתו עכבר היודע לפתור משוואות דיפרנציאליות! עקבות המאמץ הכביר ניכרו רק מעט בפניו של הד"ר פז שעה שכינס את הנהלת הטכניון יחד עם כתבים של עיתונים מתמטיים ידועי שם וכתביהם של מיטב המקומונים, לספר על ההישג המדהים. העכבר, ששמו ספידי גונזלס, פתר נכונה, לנוכח עיניהם המשתאות של הכתבים, כל משוואה שניתנה לו. כמובן, הוא אינו יודע לדבר או לכתוב, ולכן הוצגו השאלות בשיטה אמריקאית. המשוואה נכתבה לפניו על גבי לוח שחור, ולידה נכתבו ארבע תשובות, וספידי לחץ על אחד מארבעה מקשים שלידו, שהיו מסומנים במספרי התשובות. לתדהמת כולם, לא טעה ספידי ולו גם פעם אחת, וזאת בשאלות שגם מיטב החוקרים בפקולטה למתמטיקה התקשו לפתור!
(האם יש גבול לרשעות האנושית? במו אזני שמעתי תוך כדי הדגמה מישהו בקהל לוחש בקול רם מספיק בכדי שישמע מסביב: "הוא לא פותר. הוא לוקח את התשובות ומציב במשוואות, ובודק איזו מהן נכונה". לא הייתי יורדת לרמתו של האיש ומזכירה זאת, לולא נחוץ היה לתאר שוב ושוב את צרות העין שבה נתקלים פורצי דרך מסוגו של הד"ר פז.)
"הסוד", הסביר ד"ר פז בלי שמץ יהירות בקולו, "הוא בסבלנות. הלימוד נעשה כמובן על ידי התניה: על כל תשובה נכונה זכה ספידי בפרס של גבינה, ועל כל תשובה לא נכונה נענש במכת חשמל קלה אבל מכאיבה. אני עצמי הופתעתי מן המהירות שבה למד ספידי את התורה, וזאת בשעה שחסרים היו לו לגמרי מקצועות הקדם!"
מדוע טרח כל כך ד"ר פז? לאלה מביננו המכירים אותו ברור הוא שלא לשם פרסום או לשם הקוריוז שבעניין. ברור שמטרה כבדת משקל עמדה לנגד עיניו. ואכן, כידוע, לצד מחקריו פורצי הדרך עומדת בראש מעייניו של יסולא ההוראה.
"לא אחת נכמר בי לבי", אומר ד"ר פז ברגשנות שאינה רגילה אצלו "על הסטודנטים הנאנקים תחת עולם של המקצועות הקשים. במיוחד קשה לי לראותם מתענים בשיטת הציונים האכזרית. סברתי שבמקום העונש המכאיב לאורך זמן של ציון רע, יסבול הסטודנט פחות אם יקבל מכת חשמל קצרה. ואז עלה בדעתי הרעיון הפשוט (הגאוני בפשטותו, יורשה למערכת להעיר פעם נוספת,) שהסטודנטים ילמדו היטב הרבה יותר ומתוך פחות סבל אם ילמדו מול מכונה המעניקה להם פרס על תשובות נכונות, ונותנת להם שוק חשמלי אם טעו. הפרס והעונש יהיו גם מידיים הרבה יותר מאשר בשיטת הבחינות המיושנת, ולפי כל עקרונות הפסיכולוגיה יהיה הלימוד הרבה יותר יעיל."
כדי לשכנע את הנהלת הטכניון בשיטתו היה על ד"ר פז להוכיח את התזה שלו בניסוי, ואת ההוכחה סיפק לו בצורה מוחצת ספידי גונזלס. ואכן, לנוכח הצלחת הניסוי שוכנעו רשויות הטכניון ביתרונות העצומים של השיטה, והחל מן הסמסטר הבא תבוטלנה הבחינות, וכן מרבית השיעורים הפרונטליים. במקומם יתחבר כל סטודנט מספר פעמים ביום למכונה וילמד חדו"א, אלגברה ופיזיקה 1, 2, 3 על דרך ההתניה.
סטודנטים שאיתם דברנו הביעו התלהבות רבה מן השיטה החדשה. הדבר היחיד שעדיין לא הובהר הוא מה יהיה הפרס (שהרי כמות הגבינה שיכול סטודנט לאכול היא מוגבלת). ההצעה העומדת על הפרק היא תלושי אוכל למנזה, אלא שסטודנטים רבים טענו שבמקרה זה יעדיפו את מכות החשמל.
חידה לגדולים
רון אהרוני
החודש אנחנו מפרסמים שתי חידות.