נטגר גליון 8
דבר העורך
רון אהרוני
מה דעתכם על שרברב שיבוא לביתכם, יהמהם ויאמר "אי אפשר לעשות את העבודה הזאת"? אני בטוח שלפחות לא תשלמו לו. במתמטיקה כן משלמים לאנשים שמוכיחים אי אפשרות של משימות. התשלום הוא כמובן בתהילה. כמה מן התוצאות המפורסמות ביותר במתמטיקה הן מן הצורה "אי אפשר". אי אפשר לחלק זווית לשלושה חלקים שווים בעזרת מחוגה וסרגל, אי אפשר לרבע את המעגל, אי אפשר לכתוב תוכנית מחשב שבהינתן לה נוסחה בתורת המספרים היא מחליטה אם הנוסחה נכונה או לא, או אם אפשר להוכיח אותה או לא (שני האחרונים הם משפטים מפורסמים של גדל). בגיליון זה נספר על שתי תוצאות של אי אפשרות. האחת - שהשורש הריבועי של 2 הוא מספר אירציונלי, כלומר אי אפשר לכתוב אותו כמנה של שני מספרים שלמים. שני מאמרים מופיעים על כך - האחד, שלקוח מן הספר "מתמטיקה שירה ויופי", מספר על ההיסטוריה של התגלית הזאת. האחר, מאמר של אלי ברגר, אליהו לוי ומיכאל צוויקל, מספר על הוכחה יפה לתוצאה הזאת, שמשתמשת בקיפולי נייר.
מאמר שני מסוג זה הוא של יעקב רובינשטיין, על סינכרון של שעונים, ושוב - מדובר באי אפשרות. במאמר מסופר מדוע אין פונקציה שמסנכרנת שעונים (כדי להבין במה מדובר תצטרכו לקרוא את המאמר).
יש לנו גם השערת החודש, השערת "חבלים וסולמות מתמטיים", של לותר קולץ.
ואת החדשות הטובות ביותר שמרתי לסוף. הן נוגעות לאחד מגיבורי "נטגר", יסולא פז, מייסד המחלקה למתמטיקה ניסויית בטכניון. החדשות הן שסוף סוף הוא הצליח להשיג תגבור כוחות למחלקה שלו (שעד כה הייתה מחלקה של איש אחד). הכוח החדש הוא הפילוסוף השימושי שושן פנסה. במאמרה של אנה ליזהטוב על חבר הסגל החדש יסופר על הרוח החדשה והמנהגים החדשים שהכניס לפקולטה, כמו ויכוחים והתנצחויות אחרי כל הרצאה. אנחנו בטוחים ששושן יחדש עוד הרבה, וילמד את חברי הסגל קריטריונים לנכונות של אמיתות מתמטיות, ובכלל, יסביר להם מה זו "אמת".
בברכת חגים נעימים וקריאה מהנה,
העורך
הוכחת אי-רציונליות של שורשים של מספרים שלמים באמצעות קיפולי נייר
אלי ברגר, אליהו לוי, מיכאל צוויקל
שורש ריבועי (או בקיצור פשוט שורש) הוא הפעולה ההפוכה לכפל מספר בעצמו. אם $latex {\frac{4}{3} * \frac{4}{3} = \frac{16}{9}}$ אז השורש של שש עשרה תשיעיות הוא ארבעה שלישים. למה בכלל נחוצה הפעולה הזאת? מדוע אי אפשר להסתפק בחיבור, חיסור, כפל וחילוק? אחד מתחומי המתמטיקה שבו יש שימוש נרחב בשורש הוא הגיאומטריה. בפרט הוצאת שורש מופיעה כשמפעילים את משפט פיתגורס. משפט פיתגורס אומר שבמשולש ישר זווית ריבוע היתר שווה לסכום של ריבועי שני הניצבים. פירוש הדבר הוא שאם ידוע לנו מה אורך שני הניצבים ואנחנו רוצים למצוא את אורך היתר, אנחנו מחשבים את הסכום של ריבועי שני הניצבים ואז מוציאים שורש.
משפט פיתגורס קרוי על שם מתמטיקאי יווני בשם פיתגורס שחי כ- $latex {500}$ שנה לפני הספירה ואסף סביבו קבוצת אנשים שנקראה "האסכולה הפיתגוראית". באסכולה זו מצאו את משפט פיתגורס ובעזרתו גילו למשל שאם אורכי הניצבים במשולש ישר זווית הם $latex {3}$ מטרים ו- $latex {4}$ מטרים, אזי אורך היתר הוא $latex {5}$ מטרים. (כמובן, היוונים לא השתמשו במטרים אלא ביחידות מרחק אחרות.) ועכשיו נשאלת השאלה: אם אורך כל אחד מהניצבים הוא מטר אחד, מה האורך (במטרים) של היתר? לפי משפט פיתגורס, זהו המספר שהריבוע שלו הוא $latex {2}$.
אבל מהו המספר הזה? בימינו פשוט עונים לשאלה הזו בתשובה "שורש $latex {2}$" ומסמנים $latex {\sqrt{2}}$, אבל חברי האסכולה הפיתגוראית לא הסתפקו בתשובה כזו. הם רצו לדעת כמה המספר הזה בדיוק. זה מספר גדול מאחד וקטן מ- $latex {2}$. אולי אחד וחצי? לא בדיוק. אחד וחצי כפול עצמו זה $latex {2}$ ורבע. קרוב ל- $latex {2}$ אבל לא בדיוק. אז צריך פחות מאחד וחצי. אולי $latex {7}$ חמישיות? זה יותר מוצלח. הריבוע של $latex {7}$ חמישיות הוא $latex {49}$ חלקי $latex {25}$. מתקרב ל- $latex {2}$ אבל עדיין לא בדיוק. חברי האסכולה חיפשו פתרון מדויק. מנה של שני מספרים טבעיים שמכפלתה בעצמה נותנת בדיוק את המספר $latex {2}$.
האם הצליחו? לא בדיוק. או אולי יותר נכון להגיד שבדיוק להיפך. אנחנו יודעים בוודאות שהם לא הצליחו למצוא מנה כזו, אבל האגדה מספרת (כי אין תיעוד רב לדיוני האסכולה) שאחד מחברי האסכולה בשם היפאסוס הצליח לעשות דבר אחר: להוכיח שלא קיימת מנה של שני טבעיים שהריבוע שלה הוא $latex {2}$. בלשון ימינו אומרים שהוא מצא שהשורש של $latex {2}$ איננו רציונלי. כלומר השורש של $latex {2}$ גם הוא סוג של מספר, אך הוא שונה מהמספרים שהכירו עד אז. למספרים שהכירו עד אז שהם מנה של שני שלמים קוראים רציונליים ולמספרים כמו שורש $latex {2}$ שאינם כאלה קוראים אי-רציונליים.
איך גמלו להיפאסוס על הישגו? לא בהערכה רבה. לפי אחת האגדות הוא גורש מהאסכולה ולפי אחרת הוא הוצא להורג. אולי בצדק. הרי במקום לבצע את המשימה, הוא מצא תירוץ לא לעשותה. הרי גם בימינו מצפים לעשייה ולעמידה במשימה ולא להתחמקות. אבל דווקא הוכחה שמשימה היא בלתי אפשרית נחשבת לעתים כהישג חשוב לא פחות מביצוע המשימה ולפעמים אף יותר. מדוע? כי באופן מפתיע דווקא הוכחות שדבר הוא בלתי אפשרי נוטות להיות יותר יצירתיות ויותר מחכימות. על מנת להוכיח שמשימה שהוטלה עלי בלתי אפשרית, לא מספיק שאגיד "אני לא עושה ובכך מוכיח שאי-אפשר". אני צריך להראות שחוסר ההצלחה שלי נבע ממשהו מעבר לעצלות שלי או לחוסר התושייה שלי. עלי לקחת בחשבון את כל האפשרויות שעמדו בפני ולהראות שבכולן כולן הייתי נכשל במשימה. וזה דורש לא מעט כושר הפשטה, כי עלי לחשוב בעת ובעונה אחת על אפשרויות רבות. לפעמים אף קורה שכאשר מגלים שדבר מה במתמטיקה הוא בלתי אפשרי, התגלית הזו פותחת דלת לתחום חדש בעל שימושים מפתיעים.
אחת הדרכים להראות שדבר הוא בלתי אפשרי היא בדרך השלילה. אני מניח שהדבר אפשרי ואז מסיק מזה בדרך כלשהי סתירה משהו שלא יכול להיות. וכאן נכנס הדבר שהופך הוכחות של אי אפשרות לכל כך יצירתיות. אפשר לחפש את הסתירה בכל מקום שרוצים. ואכן ישנן הוכחות רבות ששורש $latex {2}$ איננו רציונלי. כל אחת מהן מוצאת את הסתירה במקום אחר. מה שנראה כאן הוא איך להשתמש לצורך כך ברעיון לא צפוי: קיפולי נייר. מקור ההוכחה שניתן כאן היא ככל הנראה במתמטיקאי ג'ון קונווי (John Conway) מאוניברסיטת פרינסטון.
בואו נעזוב רגע בצד את השורשים ואת הרציונליים וננסה את האתגר הבא: נותנים לנו משולש מנייר ואנחנו רוצים בעזרת קיפולי נייר ליצור משולש קטן יותר שדומה למשולש המקורי, כלומר עם אותן שלוש זוויות אבל אורך הצלעות קטן יותר ביחס קבוע. יש כמה דרכים לעשות את זה, אבל אנחנו נתמקד כאן בשני סוגים של משולשים שעבורם אפשר לעשות את זה על-ידי קיפול יחיד:
1. משולשים ישרי זווית,
2. משולשים שווי שוקיים שבהם אורך השוקיים ארוך מהבסיס.
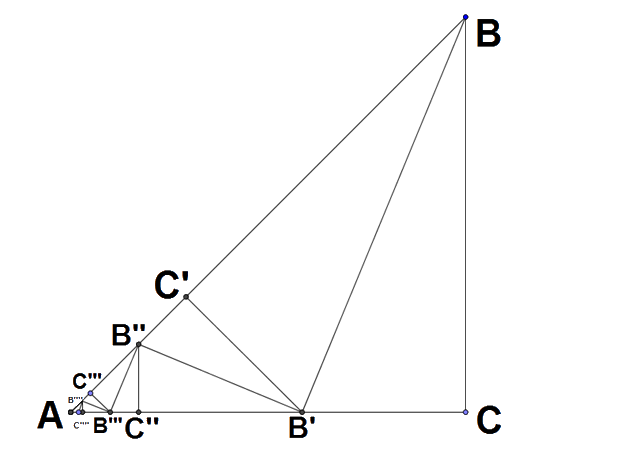
במקרה של משולש ישר זווית, נגזור את צורתו מנייר ונניח על שולחן. נתחיל לבצע את הקיפול בזה שנעביר אחד הניצבים ( $latex {BC}$ בציור כאן) כך שהוא מונח בדיוק מעל היתר ($latex {AB}$ בציור כאן). נחזיק את הניצב הזה במקום הזה ונלחץ בעדינות על כל המשולש לתוך השולחן. אז נוצר קטע ( $latex {BB'}$ בציור כאן). אם נפתח בחזרה את המשולש ניראה שהקטע החדש שיחסית אליו התבצע הקיפול הוא למעשה חוצה הזווית של $latex {\angle ABC}$. כעת המשולשים $latex {ABC}$ ו-$latex {AB'C'}$ הם דומים. בשניהם זווית ישרה ולשניהם אותה זווית בקודקוד $latex {A}$, לכן הם דומים.

איור1: קיפול ישר זווית
במקרה של משולש שווה שוקיים, שבו אורך השוקיים ארוך מהבסיס נקפל במשולש הגזור מנייר את אחת השוקים (בציור זה השוק $latex {AC}$) על עצמה, תוך שהקודקוד שאינו בשוק זו (קודקוד $latex {B}$ בציור) נשאר במקומו. הקיפול יוצר זווית ישרה בנקודה על השוק שקופלה (נקודה $latex {E}$ בציור) והקודקוד $latex {A}$ נוחת בקיפול על נקודה אחרת על השוק (נקודה $latex {D}$ בציור). אם נפתח חזרה את הנייר, נראה שהקטע $latex {BE}$ שיחסית אליו התבצע הקיפול הוא למעשה הגובה מהקודקוד $latex {B}$ לשוק $latex {AC}$. המשולשים $latex {ABC}$ ו- $latex {ADB}$ שניהם שווי שוקיים ולשניהם אותה זווית בקודקוד $latex {A}$, ולכן הם דומים.
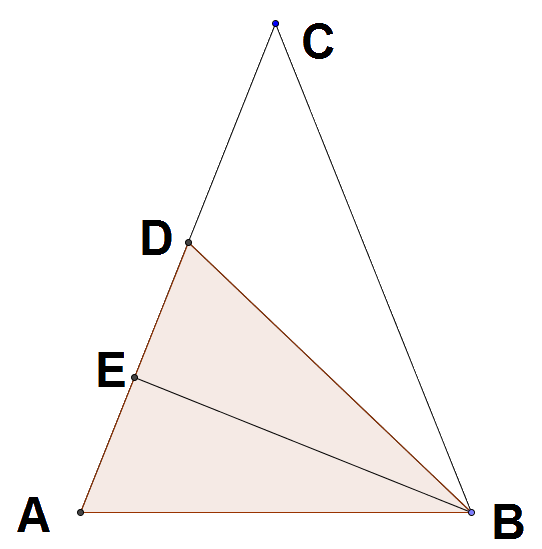
איור 2: קיפול שווה שוקיים
עכשיו הזמן להכניס את ההנחה ששורש $latex {2}$ הוא מספר רציונלי ונראה איך זה מביא לסתירה. אנחנו מניחים ששורש $latex {2}$ הוא מספר רציונלי, כלומר הוא מנה של שני מספרים שלמים, כלומר יש משולש ישר זווית ושווה שוקיים שכל צלעותיו באורך שהוא מספר שלם של מילימטרים. כעת נבצע על המשולש הזה קיפול ישר זווית (המשולש הזה אמנם גם שווה שוקיים, אבל אי אפשר לבצע עליו קיפול שווה שוקיים כי הבסיס ארוך יותר מהשוקיים) בואו נתבונן כעת באיור 1. אנחנו יודעים שאורך כל אחת מהצלעות $latex {AB}$, $latex {BC}$, $latex {AC}$ הוא שלם (כלומר מספר שלם של מילימטרים). אנחנו יודעים שהצלע $latex {BC}$ נוחתת אחרי הקיפול על הקטע $latex {BC'}$ ולכן גם האורך של הקטע הזה הוא שלם. מכאן שגם האורך $latex {AC' = AB-BC'}$ הוא שלם. עכשיו בואו ניזכר שהמשולש $latex {AB'C'}$ דומה למשולש $latex {ABC}$ ומכיוון שבמשולש $latex {ABC}$מתקיים $latex {AC = BC}$ אותו דבר קורה גם במשולש $latex {AB'C'}$ כלומר $latex {AC' = B'C'}$, כלומר קיבלנו שגם האורך $latex {B'C'}$ הוא שלם. עכשיו הזמן שוב להשתמש במסקנות מהקיפול. הקטע $latex {B'C}$ נחת בקיפול על הקטע $latex {B'C'}$ ולכן גם לו יש אורך שלם. ולבסוף, גם האורך $latex {AB' = AC-B'C}$ הוא שלם. לסיכום קיבלנו שגם המשולש $latex {AB'C'}$ מורכב משלוש צלעות שאורך כל אחת מהן הוא מספר שלם של מילימטרים.
אז איפה הסתירה כאן? הסתירה היא שלא צריך לעצור כאן. אפשר לקחת את המשולש הקטן $latex {AB'C'}$ ולבצע עליו את אותו קיפול ושוב לקבל משולש דומה לו $latex {AB"C"}$ שהוא יותר קטן אבל עדיין כל אורך כל אחת מהצלעות הוא מספר שלם של מילימטרים. ואפשר לחזור על זה שוב ושוב ושוב עד אינסוף. נקבל משולשים קטנים יותר ויותר אבל כולם באורך שהוא מספר שלם של מילימטר. אבל זה לא יכול להיות. אי אפשר למצוא סדרה אינסופית של מספרים טבעיים שיורדת עוד ועוד. בשלב כלשהו נהיה חייבים להגיע לאורכים של פחות ממילימטר, וזה עומד בסתירה למה שהראינו עכשיו שכל הזמן נשמרת התכונה שאורך כל אחת מהצלעות היא מספר שלם (וחיובי כמובן) של מילימטרים.
בזה למעשה סיימנו את ההוכחה ששורש $latex {2}$ איננו רציונלי. אבל אם הגענו עד הנה עם הרעיון הזה של קיפולי נייר, בואו ננסה להוכיח איתו עוד דברים. הדבר הבא שנוכיח הוא שחתך הזהב הוא אי-רציונלי. חתך הזהב הוא פתרון המשוואה $latex { x - \frac{1}{x} = 1}$ יש למשוואה שני פתרונות, אבל אנחנו מעוניינים בחיובי מביניהם. כדאי לציין שיתכן שדווקא חתך הזהב היה המספר הראשון שלגביו הוכיח היפאסוס שהוא אי-רציונלי. למעשה אפשר לפתור את המשוואה הריבועית ולחשב $latex {(\sqrt{5} +1)/2}$. לכן ברגע שנוכיח ש- $latex {x}$ הוא אירציונלי, נוכיח שגם $latex {\sqrt{5}}$ הוא אי-רציונלי.
אז כמו קודם נניח בשלילה ש- $latex {x}$ רציונלי, כלומר יש שני מספרים שלמים $latex {a,b}$ כך ש- $latex {x = b/a}$. כעת ניצור משולש שווה שוקיים שבו אורך השוקיים בו הוא $latex {b}$ מילימטר ואורך הבסיס הוא $latex {a}$ מילימטר. עכשיו נבצע על המשולש קיפול שווה שוקיים. בואו נתבונן כעת באיור 2. במשולש $latex {ABC}$ היחס בין השוק לבסיס הוא $latex {x}$, ולכן גם במשולש הדומה לו $latex {ADB}$ היחס בין השוק לבסיס הוא $latex {x}$. קיבלנו אם כן, $latex {AD=a/x}$. כעת אפשר לחשב
$latex {CD = b-AD = a(x - \frac{1}{x}) = a}$
שזה אומר בין יתר הדברים שהאורך של $latex {CD}$ הוא מספר שלם של מילימטרים, ולכן גם האורך $latex {AC = b- CD}$ הוא מספר שלם של מילימטרים. ושוב חוזר אותו טיעון כמו בהוכחה הקודמת. היה לנו משולש שאורך כל צלע בו הוא מספר שלם של מילימטרים ויצרנו משולש קטן ממנו ודומה שגם בו אורך כל צלע הוא מספר שלם של מילימטרים ואנחנו יכולים להמשיך בתהליך הזה עוד ועוד וזה לא יכול להיות.
בואו נעשה סיכום ביניים. הוכחנו שהשורשים של $latex {2}$ ושל $latex {5}$ הם לא רציונליים. מה לגבי השורשים של מספרים שלמים אחרים? יש שני כיוונים לחשוב על זה. או לנסות רעיון שונה לגמרי או לנסות לראות אם אפשר להכליל עוד את הרעיונות שהיו לנו עד עכשיו. יש המון רעיונות שונים לגמרי שעובדים, אבל בואו נישאר בקיפולי נייר ונראה אם אפשר בשינויים קטנים בהוכחות להשיג קצת יותר.
לשם כך צריך לעבור שוב על ההוכחות ולמצוא בהן דברים שאפשר לשנות. נסתכל למשל על ההוכחה לעיל שחתך הזהב אינו רציונלי. היה לנו טיעון כזה "ידוע ש- $latex {AB}$ שלם וידוע $latex {CD=AB}$ ולכן $latex {CD}$ שלם". אבל לא היינו צריכים בשביל זה ש- $latex {CD=AB}$. מספיק היה אילו ידענו שאורך $latex {CD}$ שווה למספר שלם כפול $latex {AB}$. גם בהוכחה ששורש $latex {2}$ הוא אי-רציונלי היה דבר דומה. היה לנו טיעון שאמר "ידוע ש- $latex {AC'}$ שלם וידוע $latex {B'C' = AC'}$, כלומר קיבלנו שגם האורך $latex {B'C'}$ הוא שלם." גם פה לא היינו צריכים את השיוויון $latex {B'C' = AC}$, והיה מספיק אילו ידענו ש-$latex {B'C' = nAC}$, עבור מספר $latex {n}$ שלם מסוים. עוד דבר שאפשר לשים לב אליו בהוכחה הוא שקודם מסיקים ש- $latex {B'C'}$ שלם ואחר-כך מסיקים ש- $latex {AB'}$ שלם. אילו היינו יכולים בדרך כלשהי להסיק ישירות ש- $latex {AB'}$ שלם היינו יכולים להפוך את סדר החישובים ולהסיק ש- $latex {B'C'}$ שלם. במשפטים הבאים נוציא לפועל את כל הרעיונות הללו.
משפט: לכל מספר $latex {n}$ טבעי, הפתרון החיובי למשואה $latex {x - \frac{1}{x} = n}$ איננו רציונלי.
הוכחה: נניח בשלילה ש- $latex {x}$ רציונלי, כלומר יש שני מספרים שלמים $latex {a,b}$ כך ש- $latex {x = b/a}$. כעת ניצור משולש שווה שוקיים שבו אורך השוקיים בו הוא $latex {b}$ מילימטר ואורך הבסיס הוא $latex {a}$ מילימטר. עכשיו נבצע על המשולש קיפול שווה שוקיים. כדאי עכשיו להתבונן באיור 2. במשולש $latex {ABC}$ היחס בין השוק לבסיס הוא $latex {x}$, ולכן גם במשולש הדומה לו $latex {ADB}$ היס בין השוק לבסיס הוא $latex {x}$. קיבלנו $latex {AD=a/x}$. ואפשר לחשב
$latex {CD = b-AD = a(x - \frac{1}{x}) = na}$
כלומר האורך של $latex {CD}$ הוא מספר שלם של מילימטרים, ולכן גם האורך $latex {AD=b-CD}$ הוא מספר שלם של מילימטרים. ושוב יצרנו משולש דומה למקורי אבל קטן ממנו שגם בו אורך כל צלע הוא מספר שלם של מילימטרים ואנחנו יכולים להמשיך בתהליך הזה עד אינסוף ולהגיע לסתירה.
הערה: אפשר לפתור את המשוואה ולקבל $latex {x = \frac{\sqrt{4+n^2}+n}{2}}$ , כך שלמעשה הוכחנו ששורש של מספר מהצורה $latex {n^2 +4}$ לעולם איננו שלם.
משפט: לכל מספר $latex {n}$ טבעי, השורש של המספר $latex {n^2 +1}$ איננו רציונלי.
הערה: למעשה אפשר להוכיח את המשפט הזה כמסקנה מהמשפט הקודם בלי קיפולי נייר בכלל, אבל נשאיר את זה כאתגר לקורא וניתן הוכחה עם קיפולי נייר.
הוכחה: נשים לב שלפי משפט פיתגורס, אם במשולש ישר זווית אורך אחד הניצבים הוא פי $latex {n}$ מהניצב השני, אזי אורך היתר הוא פי שורש של $latex {n^2 +1}$ מהניצב הקצר. אם מניחים שהשורש הזה הוא שלם, אזי אפשר ליצור משולש כזה שבו אורך כל הצלעות הוא מספר שלם של מילימטרים. כעת נבצע קיפול ישר זווית כמו באיור 1, אבל בניגוד לאיור, הניצב $latex {BC}$ הוא הארוך יותר במקרה שלנו. הצלע $latex {BC}$ נוחתת אחרי הקיפול על הקטע $latex {BC'}$ ולכן גם האורך של הקטע הזה הוא שלם. מכאן שגם האורך $latex {AC' = AB-BC'}$ הוא שלם. עכשיו בואו ניזכר שהמשולש $latex {AB'C'}$ דומה למשולש $latex {ABC}$ ומכיוון שבמשולש $latex {ABC}$ מתקיים $latex { nAC=BC}$ אותו דבר קורה גם במשולש $latex {AB'C'}$ כלומר $latex {nAC'=B'C'}$, כלומר קיבלנו שגם האורך $latex {B'C'}$ הוא שלם. הקטע $latex {B'C}$ נחת בקיפול על הקטע $latex {B'C'}$ ולכן גם לו יש אורך שלם. ולבסוף, גם האורך $latex {AB' = AC-B'C}$ הוא שלם. לסיכום קיבלנו שגם המשולש $latex {AB'C'}$ מורכב משלוש צלעות שאורך כל אחת מהן הוא מספר שלם של מילימטרים, וכשחוזרים על זה שוב ושוב זה מוביל לסתירה.
משפט: לכל מספר $latex {n}$ טבעי, השורש של המספר $latex {n^2 -1}$ איננו רציונלי.
הוכחה: נשים לב שלפי משפט פיתגורס, אם במשולש ישר זווית אורך היתר הוא פי $latex {n}$ מאחד הניצבים, אזי אורך הניצב השני הוא פי שורש של $latex {n^2 -1}$ מהניצב הראשון. אם מניחים שהשורש הזה הוא שלם, אזי אפשר ליצור משולש כזה שבו אורך כל הצלעות הוא מספר שלם של מילימטרים. כעת נבצע קיפול ישר זווית כמו באיור 1, כלומר $latex {AB = nAC}$. כמו קודם האורך של $latex {BC'}$ הוא שלם כי $latex {BC=BC'}$, וגם האורך $latex {AC' = AB-BC'}$ הוא שלם. המשולש $latex {AB'C'}$ דומה למשולש $latex {ABC}$ ומכיוון שבמשולש $latex {ABC}$ מתקיים $latex { nAB=AC}$ אותו דבר קורה גם במשולש $latex {AB'C'}$ כלומר $latex { AB' = nAC' }$, כלומר קיבלנו שגם האורך $latex {AB'}$ הוא שלם. כעת נחשב
$latex {B'C' = B'C = AC-AB'}$
ולכן גם האורך הזה הוא מספר שלם של מילימטרים. שוב קיבלנו שגם המשולש $latex {AB'C'}$ מורכב משלוש צלעות שאורך כל אחת מהן הוא מספר שלם של מילימטרים, וכשחוזרים על זה שוב ושוב זה מוביל לסתירה.
הערה: מאמר זה מבוסס על מאמר של המחבר השלישי, המופיע בכתובת
http://www2.math.technion.ac.il/~mcwikel/paperfold.pdf
המאמר המקורי מכיל נושאים נוספים.
סינכרון שעונים ביולוגיים
יעקב רובינשטיין
כל אורגניזם, בין אם בעל חיים, בקטריה או צמח, מכיל שעון ביולוגי (או אפילו מספר שעונים ביולוגיים) המכתיב ומווסת את פעולות הגוף שלו. כולנו מכירים את המחזור היומי של בני האדם (המחזור הסירקאדי) שאורכו קצת יותר מ $latex {24}$ שעות. אגב, אורך המחזור היומי משתנה מחיה לחיה והוא בדרך כלל בטווח שבין $latex {22}$ ו $latex {28}$ שעות. שעון אחר המוכר לפחות למחציתנו הוא שעון הביוץ הנשי שאורכו כ $latex {28}$ יום. יש שעונים ביולוגיים שמחזורם ארוך בהרבה. למשל, חרקים ממשפחת הציקדות (סוג של צרצרים) המכונה מאגיציקאדה חייים במצב גולם רדום מתחת פני הקרקע משך $latex {13}$ או $latex {17}$ שנים ואז מתעוררים ומתבגרים בבת אחת וממלאים חלל האויר בצרצור משולב רועש במיוחד. אגב, זמר העם האמריקאי בוב דילן היה עד להתעוררות כזו של ציקדות בשנת $latex {1970}$ בעת ששהה באוניברסיטת פרינסטון לרגל קבלת דוקטורט של כבוד שם. הוא כתב על כך את שירו המפורסם "יומו של הארבה". מתברר שמר דילן מצטיין בשירתו אך לא בידיעותיו בזואולוגיה, שכן הארבה הוא חרק ממשפחה אחרת לגמרי מאשר הציקאדה.
שאלה: האם תוכלו לחשוב על סיבה מדוע לבעלי חיים שונים מחזורי עירות שונים? מדוע מחזורי החיים של ציקאדות שונות הוא דווקא $latex {17}$ או $latex {13}$ שנים? מה, למשל, היה קורה אם קיים טורף של הציקאדות שמחזור העירות שלו הוא $latex {4}$ שנים - אילו מחזורים אינם כדאיים לציקאדות?
שאלה חשובה המעניינת חוקרים של מערכות ביולוגיות ופיזיולוגיות היא כיצד שעונים ביולוגיים מסתנכרנים. נניח למשל שני שעונים ביולוגיים הבאים במגע זה עם זה ומראים "שעות" שונות. אם יש להם תפקיד דומה, רצוי מאוד שיורו את אותה השעה, או יהיו מתואמים באיזה אופן אחר. למשל, התאים הנמצאים באזור הלב המכונה קישורית סינו-אטריאלית אחראים לקצב אחיד של פעימות לב. הם עושים זאת ע"י פעולה מתואמת (מסונכרנת). מתברר ששאלת הסינכרון של שעונים מעוררת בעיות מתמטיות מעניינות. להמחיש זאת, נדון בשאלה הפשוטה ביותר: האם אפשרי בכלל לצמד שעונים להסתנכרן באופן אוטומטי, ללא יד מכוונת?
כדי להשיב על השאלה נתחיל בהגדרה יותר מדויקת שלה. נגדיר שעון כתנועה על פני מעגל $latex {C}$ ברדיוס $latex {\frac{1}{2\pi}}$. השעה שהשעון מראה היא המרחק לאורך הקשת מנקודה שרירותית שנסמן ב $latex {0}$. למשל, השעון הימני באיור 1 מתאר את השעה $latex {0.25}$, ואילו השעון השמאלי באיור מתאר את השעה $latex {0.5}$. נשים לב כי מאחר שהתנועה מחזורית, הרי שהשעה $latex {0.99}$ קרובה מאוד לשעה $latex {0.01}$. המרחק בין שתי נקודות זמן אלה הוא $latex {0.02}$. דרך חליפית לתאר שעון מעין זה הוא כתנועה על הקטע $latex {[0,1]}$, כאשר אנו מזהים את הנקודה $latex {1}$ עם הנקודה $latex {0}$. בהמשך נשתמש על פי הנוחות שלנו בשתי הדרכים החליפיות שתיארנו עבור שעון.
נניח שלפנינו שני שעונים שברצונם להסתכרן. נסמן את השעה שמראה השעון הראשון ב $latex {x}$ ואת השעה שמראה השעון השני נסמן ב $latex {y}$. נגדיר גם את ריבוע היחידה
$latex \displaystyle D=\{x,y| 0 \leq x \leq 1,\; 0 \leq y \leq 1\},$
תוך שמירה על מחזוריות כלומר, כל קודקוד מזוהה עם הקודקוד המתאים לו $latex {\mod 1}$. פעולת הסינכרון היא פונקציה $latex {f(x,y)}$ המתאימה לזמנים שמראים שני השעונים זמן חדש לכל ערך רגעי שלהם $latex {(x,y)}$ בעת פעולת הסינכרון. כמובן שגם ערכי הפונקציה $latex {f}$ מתארים שעה, כלומר נקודה על פני המעגל $latex {C}$. מתכונת המחזוריות של השעונים מתקיים
$latex \displaystyle f(0,0)=f(1,0)=f(0,1)=f(1,1). \ \ \ \ \ (1)$
שיטת סינכרון טריוויאלית היא לבחור שעה מוסכמת על כל השעונים. כלומר $latex {f(x,y)=f_0}$ לכל $latex {(x,y)}$, כאשר $latex {f_0}$ הוא מספר ממשי כלשהו ב $latex {[0,1]}$. אבל זהו סינכרון שרירותי לא מעניין, וכפי שנראה מיד גם לא יעיל. בפרט, לא ברור מה מיוחד דווקא במספר $latex {f_0}$? שיטה אחרת היא שאחד השעונים, נגיד הראשון, קובע את השעה לשניהם. כלומר $latex {f(x,y)=x}$. אבל זו שיטה לא דמוקרטית! מדוע שהשעון השני יסכים לציית לראשון?
אם כן, אנו רוצים למצוא פונקצית סינכרון מעניינת, וגם שוויונית. קל לראות שתכונת השוויוניות גוררת את תכונת הסימטריה
$latex \displaystyle f(x,y)=f(y,x). \ \ \ \ \ (2)$
תכונה רצויה נוספת היא יעילות: אם במקרה שני השעונים כבר מסונכרנים, אין צורך לעשות דבר. מתמטית תכונה זו מכתיבה
$latex \displaystyle f(x,x)=x. \ \ \ \ \ (3)$
תכונה טבעית נוספת שנדרוש מפונקצית הסינכרון היא רציפות של $latex {f}$. הגדרה מדויקת של מושג הרציפות אינה פשוטה למרות שהמלומדת אנה ליזהטוב הציגה בשני מאמריה המאלפים בגליון נט-גר של יוני $latex {2014}$ צעדים ראשונים לכך. מספיק למטרתנו לחשוב על רציפות של פונקציה באופן אינטואיטיבי: אם משנים את משתנה הפונקציה קצת, אז גם ערך הפונקציה משתנה קצת, כשהמילה 'קצת' קשורה למושג האפסילון שתואר כאמור למעלה ע"י ליזהטוב. בפרט, לפונקציה רציפה אין קפיצות.
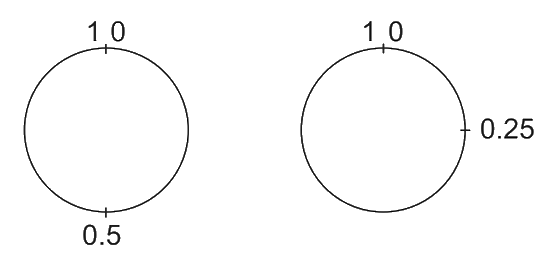
דוגמאות למצבי שעונים
מצוידים בהגדרות של בעיית הסינכרון ובשלוש דרישות מפונקציה זו (סימטריה, יעילות ורציפות), ניגש לשאלה כיצד בונים פונקציה כזו? ניחוש ראשון של אנשים רבים הוא לבחור את הממוצע של השעונים, כלומר
$latex \displaystyle \bar{f}(x,y)=\frac{x+y}{2}.$
ברור שדוגמא פשוטה זו מקיימת את תכונת היעילות והסימטריה. אבל האם היא רציפה? התשובה שלילית, כי קל לחשב
$latex \displaystyle \bar{f}(0.5,0.999)=0.7495,\;\;\; \bar{f}(0.5,0.001)=0.2505.$
כלומר, שינוי מזערי של $latex {0.002}$ בערך של $latex {y}$ הוביל לשינוי גדול של כמעט $latex {0.5}$ בערך של $latex {\bar{f}}$. מתברר שכשלון הדוגמא $latex {\bar{f}}$ אינו מקרי. למעשה הבניה המבוקשת אינה אפשרית!
משפט: לא קיימת פונקצית סינכרון $latex {f(x,y)}$ שהיא סימטרית, יעילה ורציפה.
הוכחות קיום הם לעיתים קרובות ישירות, כמו למשל אלגוריתם לבניית האובייקט הרצוי. אבל הוכחות אי קיום שונות מהותית כי עלינו להבטיח שלא רק אנו נכשלנו במציאת הפונקציה $latex {f}$, אלא שכל אחד ייכשל במשימה זו. נוכיח את המשפט בעזרת אובייקט מתמטי מעניין וחשוב המכונה דרגה. נעיר שההוכחה שנציג היא מעט היוריסטית, כלומר לא פורמלית, כי מושג הרציפות לא הוגדר כאן במדויק.
נניח אם כן שקיימת פונקציית סינכרון $latex {f(x,y)}$ שהיא יעילה, סימטרית ורציפה. נסמן ב $latex {M}$ מסלול סגור ב $latex {D}$, כמשורטט באיור 2, ותהא $latex {A}$ נקודה כלשהי על המסלול $latex {M}$. נתחיל לנוע על פני המסלול $latex {M}$ מהנקודה $latex {A}$ בכיוון השעון עד שנשוב לנקודה $latex {A}$ לאחר הקפה אחת של $latex {M}$. תנועה זו על פני נקודות שונות $latex {(x,y)}$ בתחום $latex {D}$ גוררת תנועה של $latex {f}$ על פני המעגל $latex {C}$ המתחילה ומסתיימת בנקודה $latex {f(A)}$. במהלך התנועה, $latex {f}$ עשויה להקיף את המעגל מספר פעמים. למשל היא עשויה להקיף אותו פעמיים בכיוון השעון, או אולי פעם אחת נגד כיוון השעון, או לא להקיפו כלל ולהישאר כל זמן התנועה על $latex {M}$ ליד הערך הראשוני שלה $latex {f(A)}$. אנו מכנים את מספר הפעמים ש $latex {f}$ הקיפה את המעגל $latex {C}$ בעת תנועה על המסלול הסגור $latex {M}$ הדרגה של $latex {f}$ ביחס ל $latex {M}$, ומסמנים זאת $latex {deg_M(f)}$. כאשר ההקפות של $latex {f}$ הן בכיוון השעון הן תיספרנה במספרים חיוביים, וכאשר ההקפות נגד כיוון השעון נמנה אותן כמספרים שליליים. לכן $latex {deg_M(f)}$ היא מספר שלם, חיובי, או שלילי, או אפס.
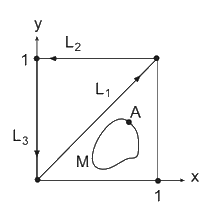
מסלולים לחישוב דרגה
נחשב כעת את הדרגה של $latex {f}$ ביחס למסלול המיוחד $latex {L}$ המשורטט אף הוא באיור 2. המסלול $latex {L}$ מורכב משלושה קטעים. הקטע הראשון $latex {L_1}$ הוא האלכסון המחבר את הנקודות $latex {(0,0)}$ ו $latex {(1,1)}$. הקטע השני $latex {L_2}$ הוא הישר המחבר את הנקודות $latex {(1,1)}$ ו $latex {(0,1)}$, והקטע השלישי $latex {L_3}$ הוא הישר המחבר את הנקודות $latex {(0,1)}$ ו $latex {(0,0)}$. תכונת היעילות $latex {f(x,x)=x}$ מבטיחה שעל פני הקטע $latex {L_1}$ הפונקציה $latex {f}$ משלימה בדיוק סיבוב אחד על פני המעגל $latex {C}$ בכיוון השעון. אמנם אין לנו מידע על הערכים של $latex {f}$ בקטע $latex {L_2}$, אבל מאחר ש $latex {f(1,1)=f(0,1)}$, נובע ש $latex {f}$ מבצעת במהלך התנועה מספר שלם (אולי $latex {0}$) של סיבובים במעגל $latex {C}$. נסמן מספר זה ב $latex {d}$. שיקול דומה, ותכונת הסימטריה $latex {f(x,y)=f(y,x)}$ מראה שגם בתנועה לאורך הקטע $latex {L_3}$ השעון $latex {f}$ משלים $latex {d}$ הקפות סביב המעגל $latex {C}$.
אם נסכם את סך ההקפות של $latex {f}$ סביב $latex {C}$ ביחס למסלול $latex {L}$ נקבל את הנוסחא
$latex \displaystyle deg_L(f)=1+2d.$
אמנם הערך של $latex {d}$ לא ידוע, אבל מסקנה מועילה מהחישוב שעשינו היא שהדרגה של $latex {f}$ ביחס ל $latex {L}$ היא מספר אי זוגי, ובפרט גילינו שהדרגה שונה מאפס.
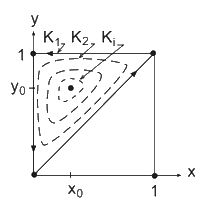
מסלולים המתכנסים בהדרגה לנקודה קבועה
נבנה כעת סדרה של מסלולים $latex {K_n}$ המתחילים ב $latex {L}$, כלומר $latex {K_1=L}$ ומתקרבים 'לאט' לנקודה $latex {(x_0,y_0)}$ כמשורטט באיור 3. כיוון שהמסלול $latex {K_2}$ קרוב מאוד למסלול $latex {K_1=L}$, ומכיוון שלפי ההנחה $latex {f(x,y)}$ פונקציה רציפה, אנו מצפים שהדרגה של $latex {f}$ ביחס ל $latex {K_2}$ תהיה קרובה מאוד לדרגה של $latex {f}$ ביחס ל $latex {K_1}$. אבל דרגה היא לפי הגדרה מספר שלם, לכן היא אינה יכולה להשתנות 'מעט', אלא אם כן השינוי הוא אפס. כלומר
$latex \displaystyle deg_{K_2}(f)=deg_{K_1}(f) =1+2d \neq 0.$
באופן דומה נקבל לכל $latex {j>1}$
$latex \displaystyle deg_{K_{j+1}}(f)=deg_{K_j}(f) =1+2d \neq 0.$
אבל, עבור $latex {j}$ גדול מאוד, המסלול $latex {K_j}$ קרוב מאוד לנקודה $latex {(x_0,y_0)}$. לכן מתקבל שפונקצית הסינכרון $latex {f}$ משתנה במידה רבה, שהרי היא עושה לפחות הקפה אחת סביב המעגל $latex {C}$, בעוד שהמשתנים שלה $latex {(x,y)}$ כמעט קבועים, וזו סתירה לרציפות $latex {f}$. מ.ש.ל.
הרמוניות מתמטיות
רון אהרוני
כמו כל בעלי החיים, גם האדם הוא יצור שמכוון אל העתיד. עיניו קבועות בקִדמת ראשו, מתוך מטרה לאסוף אינפורמציה על המקום שבו הוא עתיד להיות, ולא על המקום בו היה. מחשבותיו נתונות ברובן לעתידו, לא לעברו. הסיבה היא, בפשטות, שכך עוצבו בעלי החיים על ידי האבולוציה. האבולוציה בררה אותן צורות חיים שבעליהן יודעים היטב לכוון עצמם אל העתיד, לשרוד ולהשאיר אחריהם ("אחריהם" בזמן!) צאצאים. תועלתה של הכרת הסדר היא על כן ביכולת לצפות את העתיד. הדבר מסביר את ההנאה שמסב לנו הקצב במוזיקה, משום שקולות קצובים הם צפויים. כשאנו שומעים נקישות תוף קצובות אנחנו יודעים בדיוק מתי תישמע הנקישה הבאה. אלא שכאמור, קצב קבוע לחלוטין הוא צפוי מדי, ולכן אינו מעורר תחושת יופי. איננו מגייסים אנרגיה כדי לנבא אותו, וממילא גם אין אנרגיה שיכולה להיחסך. כדי לעורר תחושת יופי צריך הקצב להיות מורכב דיו, שלא נוכל לפענח אותו בצורה מודעת.
ההנאה מן ההרמוניה מציבה חידה קשה יותר. תופעה מוזרה היא שיש צירופי צלילים נעימים לאוזן, ויש צירופים נעימים פחות. למשל, צליל דוֹ תואם היטב את צליל דוֹ הגבוה ממנו באוקטבה. למעשה, כשמשמיעים אותם בו זמנית קשה להבחין שאלו הם שני צלילים שונים. כך גם הצמדים דוֹ-סוֹל, ו-דוֹ-מי. הצלילים דוֹ-מי-סוֹל מהווים את האקורד (צירוף צלילים) הבסיסי של סולם "דוֹ מז'ור", שהוא אולי המוכר והבסיסי בין הסולמות, משום שבפסנתר צליליו מנוגנים על הקלידים הלבנים בלבד. יצירה בסולם דוֹ מז'ור תפתח לעתים קרובות בצלילים דו-מי-סוֹל (בסדר כלשהו), תסטה מהם, תנדוד מהם והלאה ולבסוף תחזור אליהם. המוזיקה בנויה על מתח בין סטיות מן ההרמוניה לבין ההרמוניה.
אבל מה עומד מאחורי ההרמוניה? מה עושה צירוף אחד לנעים, ואחר לצורם? למרבה ההפתעה, התשובה לכך היא מתמטית, והיא התגלתה בידי אחת הדמויות הצבעוניות ביותר בתולדות המתמטיקה – פיתָגוֹרָס. פיתגורס היה מייסד ומנהיג של חבורה מסוג נדיר: כת דתית מתמטית. הכת מנתה כ-600 איש ואישה, שהתגוררו במושבה היוונית קרוֹטוֹן שבדרום חצי האי האפֶּניני, הלא הוא איטליה של ימינו, ועסקו בלימוד ובמחקר. את כל רכושם תרמו לקהילה, ואת תגליותיהם נשבעו לשמור בסוד. פיתגורס עבר יום אחד ליד בית מלאכתו של נפח, ושם לב שכאשר הנפח היכה במוטות שהיחס בין אורכיהם הוא פשוט, נאמר – שאחד מהם ארוך בדיוק פי 2 מן השני, או פי $latex \frac{3}{2}$, צירוף שני הצלילים נשמע נעים, בעוד שכאשר היחס לא היה פשוט הצירוף היה צורם.
במונחי ימינו, מבטאים זאת בכך שאם שני צלילים נשמעים טוב יחד, אז יש יחס פשוט בין התדרים שלהם. "תדר" של צליל הוא מספר הריטוטים לשנייה בהשמעתו, או בלשון מדויקת יותר: מספר השיאים לשנייה של גלי הקול. אם הצליל מופק על ידי מיתר, זהו מספר ריטוטי המיתר לשנייה. פער של אוקטבה בין צלילים (כמו בין דוֹ נמוך לדוֹ גבוה) פירושו יחס של 2 בין התדירויות שלהם: דוֹ גבוה הוא בעל תדירות כפולה מאשר הדוֹ שמתחתיו. לצליל הסוֹל, החמישי באוקטבה (כאשר מתחילים מדוֹ), יש תדר גדול פי $latex \frac{3}{2}$ מאשר לצליל הדוֹ הנמוך של אותה אוקטבה. כלומר, על כל 2 ריטוטים של מיתר הדו בפסנתר יהיו 3 ריטוטים של מיתר הסוֹל. גם ביניהם יש אפוא יחס פשוט – 3:2. היחס בין צליל מי לצליל דוֹ הוא 5:4 – אף הוא יחס מספרי פשוט למדי. זוהי הסיבה לכך שדוֹ, מי וסוֹל נשמעים טוב יחד.
פיתגורס מגלה את הקשר בין הרמוניה ומספרים
מתוך תורת המוזיקה של פרנצ'ינו גפוריו, מילאנו 1492
עד כאן ההסבר המתמטי, אבל אין בכך עדיין הסבר להנאה. כדי להבין את מקור ההנאה מצירופי צלילים בעלי יחסי תדרים פשוטים היו נחוצות עוד כ-2400 שנים. מי שגילה זאת היה המתמטיקאי, הפיזיקאי והפיזיולוג הגרמני הרמן פון הֶלְמהוֹלץ (1821 - 1894), שהסביר את ההנאה מן ההרמוניה בתופעה שנקראת "צלילים עיליים". כאשר מיתר רוטט בתדר מסוים, הוא רוטט באותה עת גם בתדר גדול פי 2, ובתדרים גדולים פי 3, 4 וכו'. הריטוטים המִשניים חלשים יותר, והם חלשים ככל שהיחס גדול יותר (אין כמעט ריטוט בתדר גדול פי 11, נאמר), אבל הם נשמעים. כלומר, כשמשמיעים לנו דוֹ, במרבית המקרים אנחנו שומעים גם את צליל הדוֹ הגבוה באוקטבה, בעל התדר הכפול ממנו, וגם את הסוֹל באוקטבה הגבוהה יותר, שהוא בעל תדר גבוה בדיוק פי 3 מאשר צליל הדו. יחס פשוט בין שני תדרים פירושו קיום צלילים עיליים משותפים לשניהם. למשל, לדוֹ ולסוֹל באותה אוקטבה משותף הצליל העילי סוֹל באוקטבה גבוהה יותר: הוא גבוה פי 3 מן הדוֹ, ופי 2 מן הסוֹל הנמוך. הוא גם לא רחוק משניהם, ולכן יופיע בצורה משמעותית. כך קורה שכאשר משמיעים לנו יחד צלילים כאלה, אנחנו מגלים סדר סמוי. האוזן מזהה את שני הצלילים כשונים, אבל בלי שנדע זאת אנו מגלים שיש לשניים גורם משותף, מה שהופך את תפיסתם לקלה יותר. ברעש שנשמע מתחילה לא מאורגן התגלה סדר מפתיע. כמובן, בכך אין להסביר את ההתרגשות שיכולה לעורר בנו המוזיקה, התרגשות שהיא כנראה פרי משחק בין דיסהרמוניה והרמוניה, אבל זהו הצעד הראשון להבנה.
כל זה היה כמובן מעֵבר לידיעותיהם של היוונים הקדמונים, שלא ידעו מהם תדרים של צלילים. וכשלא יודעים, מפנטזים. כדי להסביר את תופעת ההרמוניה המציאו פיתגורס וחבורתו תיאוריות מרחיקות לכת, בדבר כוחותיהם המאגיים של המספרים ושל היחסים ביניהם. "העולם הוא מספר", הייתה סיסמתם. כלומר, העולם נשלט על ידי יחסים מספריים פשוטים. כל דבר חשוב בטבע אמור היה לשיטתם של הפיתגוריאנים לציית לחוקים מספריים. הם סברו שיש יחסים פשוטים בין הקְטָרים של מסלולי כוכבי הלכת, ושעקב כך כוכבי הלכת משמיעים "מוזיקה שמימית". מעבר לכך, הם האמינו שכל גודל משמעותי בעולם חייב להיות ניתן לביטוי כמספר שהוא יחס בין מספרים שלמים.
מספר שהוא מנה של שני מספרים שלמים נקרא "מספר רציונלי" ("רציו" פירושו "יחס"). המספרים השלמים הם רציונליים – 4 למשל הוא רציונלי משום שהוא היחס בין עצמו ובין 1, כלומר 4:1 = 4. כל שבר הוא רציונלי, משום שקו השבר הוא למעשה סימן חילוק: $latex \frac{17}{3}$ , למשל, הוא 17:3. הפיתגוריאנים האמינו אפוא שכל גודל חשוב בטבע חייב להיות ניתן לביטוי כמספר רציונלי.
התפכחות
הישגיהם האינטלקטואליים של היוונים הקדמונים היו בבחינת נס. מתי מעט, כמה מאות אלפים, פיתחו מערכות מושגים שמפירותיהן אנחנו מתפרנסים עד עצם היום הזה. מה שדחף אותם לכך היה כבוד אינסופי בפני מושגים מופשטים. להפשטות הם ייחסו כוח מאגי, ובעיניהם הן קדמו לעולם הממשי. היוונים היו הראשונים שחקרו מושגים מופשטים בפני עצמם, ללא קשר לתועלתם בעולם החיצוני. אומנם, גם המצרים והבבלים חקרו מספרים, אבל הם עשו זאת לצרכים מעשיים. היוונים היו הראשונים שראו במספרים עולם ראוי למחקר בשל יופיו וההרמוניות הפנימיות שלו.
אבל אפילו על רקע מכלול תרומותיהם של היוונים מתבלטת הגיאומטריה כמיוחדת במינה. בה הם פיתחו את מושג ה"אקסיומה" וה"הוכחה", ובה הגיעו למידת ההפשטה המרובה ביותר. אחד מאבות הגיאומטריה היוונית היה פיתגורס עצמו. על שמו (לא לגמרי בצדק) נקרא גם המשפט שנחשב עד היום (בצדק גמור) למשפט הגיאומטרי החשוב והשימושי ביותר: "משפט פיתגורס". המשפט אומר ששטח הריבוע הבנוי על היתר של משולש ישר זווית שווה לסכום שטחי הריבועים הבנויים על הניצבים. חשיבותו של המשפט הזה היא בכך שהוא מאפשר לחשב אורכי קטעים.

משפט פיתגורס: סכום שטחי הריבועים הקטניםת הנשענים על ניצבי המשולש ישר הזוית, שווה לשטח הריבוע הגדול, הנשען על היתר של המשולש.
הנה מקרה פרטי מעניין של המשפט. נתבונן בריבוע שאורך צלעו 1. האלכסון של הריבוע הוא היתר במשולש ישר זווית, ששני ניצביו הם באורך 1.

על פי משפט פיתגורס, אורך האלכסון של ריבוע שצלעו באורך 1 הוא $latex \sqrt{2}$
ממשפט פיתגורס נובע אפוא שריבועו שווה ל: $latex 1^2 + 1^2 = 2$ . לפיכך אורכו של האלכסון הוא $latex \sqrt{2}$ . למשפט פיתגורס הכללי ידועות מאות הוכחות, חלקן קצרות ופשוטות, אבל הוכחת המקרה הזה של המשפט פשוטה במיוחד. אפשר למצוא אותה במקום מפתיע במקצת - דיאלוג מפורסם של סוקרטס בשם "קְרִיטיאַס". התבוננו בשרטוט הבא:
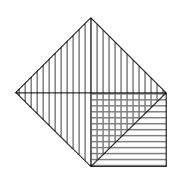
שטח הריבוע הנטוי באלכסון (מפוספס אנכית) גדול פי 2 משטח הריבוע הקטן (מפוספס אופקית), משום שהוא מכיל 4 משולשים, בעוד הריבוע הקטן בנוי משני משולשים. על כן צלעו של הריבוע הגדול פי $latex \sqrt{2}$ מצלע הריבוע הקטן.
נניח שאורך צלע הריבוע הקטן (המסומן בפסים אופקיים) הוא 1. שטח הריבוע הקטן הוא אז $latex 1*1$ , כלומר 1. הריבוע הגדול, הניצב בשיפוע(המסומן בפסים אנכיים), מורכב מ-4 משולשים, בעוד שהקטן מורכב רק משני משולשים (כל המשולשים חופפים). לכן שטח הריבוע הגדול הוא פי 2 משטח הריבוע הקטן, כלומר 2. אורך צלעו של ריבוע כלשהו הוא השורש הריבועי של השטח שלו, ולכן אורך צלע הריבוע הגדול הוא $latex \sqrt{2}$. אבל שימו לב: צלע הריבוע הגדול היא בדיוק האלכסון של הריבוע הקטן! לכן אורך האלכסון הזה הוא $latex \sqrt{2}$.
למי שהגיאומטריה עומדת במרכז עולמו, אלכסון של ריבוע הוא ללא ספק גודל טבעי. על פי האמונה הפיתגוריאנית, האלכסון הזה אמור על כן להיות מבוטא באמצעות יחס פשוט בין מספרים שלמים. כלומר, עליו להיות מספר רציונלי. במשך זמן רב ניסו הפיתגוריאנים לבטא את $latex \sqrt{2}$ כמספר רציונלי. לבסוף נוכחו בעובדה מפתיעה, ומבחינתם הרסנית: שהדבר אינו אפשרי. $latex \sqrt{2}$ אינו רציונלי.
בשל סודיותה של כת הפיתגוריאנים, רב הנסתר בתולדותיה על הנגלֶה. קרוב לוודאי שרבות מן ה"עובדות" המסופרות עליה הן המצאות מאוחרות. על פי אחד הסיפורים, התגלית ש-$latex \sqrt{2}$ אינו רציונלי הייתה לבני הכת מכה כה קשה, שהם נשבעו זה לזה לא להוציא את הסוד אל העולם החיצוני. על פי הסיפור הזה, אחד מבני הכת שגילה את הסוד שילם על כך בחייו.
מדוע $latex \sqrt{2}$ אינו מספר רציונלי
גילויים של המספרים האי-רציונליים היה מהפכה מתמטית אמיתית, שמלוא משמעויותיה עתיד היה להתברר רק במאה ה-19. אז הבינו המתמטיקאים שהמספרים הרציונליים הם רק חלק קטן מעולם המספרים, וכי ה"חורים" ביניהם, שהם המספרים האי-רציונליים, מרובים מן המספרים הרציונליים עצמם. כל זה התחיל מן התגלית ש-$latex \sqrt{2}$ אינו רציונלי.
ובכן, מדוע $latex \sqrt{2}$ אינו רציונלי, כלומר אינו ניתן לביטוי כ-$latex \frac{m}{n}$ לשום זוג של מספרים שלמים,$latex m$ ו-$latex n$? נַראה זאת על דרך הדוגמה. מספר רציונלי הקרוב מאוד ל-$latex \sqrt{2}$ הוא $latex \frac{7}{5}$. הרי $latex \sqrt{2}$ הוא מספר שריבועו הוא 2, ואילו $latex (\frac{7}{5})^2$ שווה ל-$latex \frac{49}{25}$, שהוא קרוב מאוד ל-2 (הרי $latex 2=\frac{50}{25}$). אבל מראש אפשר היה לדעת שלא ייתכן ש-$latex (\frac{7}{5})^2$ יהיה בדיוק 2, משום ש-7 הוא מספר אי-זוגי. כידוע $latex (\frac{7}{5})^2 = \frac{7^2}{5^2}$, ולו היה מתקיים $latex \frac{7^2}{5^2} = 2$, היינו מקבלים $latex 7^2 = 5^2 *2$. מכיוון ש-7 אי-זוגי, גם ריבועו אי-זוגי (הריבוע של 7 הוא $latex 7*7$, ומכפלת שני מספרים אי-זוגיים היא אי-זוגית). אגף שמאל בשוויון הוא על כן אי-זוגי, בעוד שאגף ימין הוא זוגי, משום שמופיע בו הגורם 2, כלומר השוויון לא ייתכן. אבל שימו לב – הטיעון הזה יהיה נכון לכל שבר שהמונה שלו אי-זוגי. הראינו בכך ששבר שהמונה שלו אי-זוגי אינו יכול להיות שווה ל-$latex \sqrt{2}$.
הטיעון יסתיים אם נראה גם ששבר שהמונה שלו זוגי לא יכול להיות שווה ל-$latex \sqrt{2}$. ובכן, נניח שהמונה זוגי. במקרה זה מותר להניח שהמכנה הוא אי-זוגי: אם גם המכנה זוגי, אפשר לצמצם את השבר ב-2. גם כאן יהיה נוח להסתכל בדוגמה. גם המספר $latex \frac{10}{7}$ קרוב מאוד ל-$latex \sqrt{2}$ - $latex (\frac{10}{7})^2=\frac{100}{49}$, שהוא קרוב מאוד ל-$latex \frac{100}{50}$, שהוא 2. אבל כמו במקרה הקודם, אפשר לדעת מראש ש-$latex \frac{10}{7}$ אינו שווה בדיוק ל- $latex \sqrt{2}$. לו היה $latex \frac{10}{7}=\sqrt{2}$, היה מתקיים: $latex (\frac{10}{7})^2=2$, כלומר:$latex 10^2 = 7^2*2 $ . מכיוון ש-10 הוא מספר זוגי, הריבוע שלו מתחלק ב-4 (הוכיחו לעצמכם שזוהי תכונה כללית של מספרים זוגיים!) בעוד שאגף ימין הוא מכפלת מספר אי-זוגי ב- 2, ומכפלה כזו אינה מתחלקת ב-4! אם כך, גם כאן לא ייתכן שוויון. הטיעון השתמש רק בכך שהמונה של השבר היה זוגי, ו-$latex \sqrt{2}$ אינו יכול על כן להיות גם שבר שהמונה שלו הוא זוגי. יחד הראינו ש-$latex \sqrt{2}$ אינו יכול להיות שבר בכלל!
קיימת גם דרך קצרה יותר לומר אותו דבר, אבל היא גם קצת יותר מופשטת. נניח, מתוך מטרה לקבל סתירה, ש-
$latex \sqrt{2}=\frac{m}{n}$, כאשר $latex m$ ו-$latex n$ מספרים שלמים. משמעות הדבר היא ש -$latex 2=(\frac{m}{n})^2=\frac{m^2}{n^2}$ . נעביר אגפים ונקבל: $latex 2n^2=m^2$. מספר גורמי 2 ש-$latex m^2$ מכיל הוא זוגי: למשל אם $latex m=1000=2^3*5^2$(ואז $latex m$ מכיל את 2 שלוש פעמים) אז $latex m^2 = 2^6*5^4$ מכיל את 2 שש פעמים – פי 2 יותר מאשר $latex m$ עצמו. בדומה, $latex n^2$ מכיל מספר זוגי של גורמי 2. אבל אז $latex 2n^2$ מכיל מספר זוגי+1 של גורמי 2 (בגלל הכפל ב-2), כלומר מספר אי-זוגי של גורמי 2. אם כן, $latex 2n^2$ מכיל מספר שונה של גורמי 2 מאשר $latex m^2$, ולכן לא ייתכן ש -$latex 2n^2 = m^2$ , שהיא הסתירה המיוחלת.
איך מבטאים אפוא את $latex \sqrt{2}$? אחת הדרכים היא בצורת שבר עשרוני אינסופי: $latex \sqrt{2} =1.4142135623…$. השוו זאת עם $latex \frac{7}{5}=1.4$, ועם $latex \frac{10}{7}=1.428571428571…$. שימו לב: $latex \sqrt{2}$ נמצא כמעט בדיוק באמצע ביניהם! אבל, כמובן, לא בדיוק באמצע: האמצע הוא שבר, ואנו יודעים ש-$latex \sqrt{2}$ אינו שבר.
מספרים עולים ויורדים
רון אהרוני
הבעיה הבאה, שהומצאה על ידי לותָר קולָץ (Lothar Kollatz) הגרמני ב-1937, היא משחק "סולמות וחבלים" מתמטי. עולים ויורדים בסדרה, על פי הכלל הבא: כשמגיעים למספר זוגי מחלקים אותו ב-2; כשמגיעים למספר אי זוגי כופלים אותו ב-3 ומוסיפים 1. נניח, כדוגמה, שמתחילים מ-10. מכיוון ש-10 זוגי, עלינו לחלקו ב-2. התוצאה, 5, אינה זוגית, ועל כן יש לכפול אותה ב-3 ולהוסיף 1. הגענו ל-16, שהוא זוגי, ועל כן נחלקו ב-2. הסדרה המתקבלת היא:$latex 10,5,16,8,4,2,1$. אם מתחילים מ-100 מקבלים את הסדרה:
$latex 100,50,25,76,38,19,58,29,88,44,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1$
בשני המקרים הגענו לבסוף ל-1. השערתו של קולץ היא שכך קורה תמיד - לא משנה מהיכן נתחיל, הסדרה תסתיים ב-1. כשקולגה שלי היה צריך לספר על השערות מתמטיות לילדי הכיתה של בתו, הוא בחר בבעיה הזאת – כה פשוט הוא ניסוחה. ועם זאת, ועל אף עבודה אינטנסיבית על ההשערה, לא הייתה שום התקדמות של ממש בכיוון פתרונה. קל לנסות את ההשערה במחשב, ועד כה היא אומתה בכל המקרים שנבדקו, אבל כיום אין ולו גם קצה חוט להוכחה. המתמטיקאי ההונגרי פאול ארדש אמר פעם ש"למתמטיקה של ימינו אין כלים לגשת לבעיה הזאת".
מדוע אם כן מאמינים בכל זאת בהשערה? יש סיבה "היוריסטית", כלומר לא מדויקת, להאמין בנכונותה. הסיבה היא שיש יותר "חבלים" מאשר "סולמות". אומנם, הסולמות ארוכים יותר, משום שכאשר עולים כופלים ב-3, ומוסיפים 1, בעוד שכאשר יורדים מחלקים רק ב-2. אולם כנראה מספר הירידות גדול יותר, משום שלאחר כל עלייה באה ירידה. עלייה מתרחשת כשמגיעים למספר אי זוגי; אבל כפל מספר אי זוגי ב-3 נותן מספר אי זוגי, ולאחר הוספת 1 מתקבל מספר זוגי, שבו על פי הכלל יורדים. הנחה שאין לה הוכחה אבל הכול מאמינים בה היא שלאחר כל ירידה יש עדיין סיכוי של 50% לרדת שוב, ואחר כך שוב סיכוי של 50% לרדת, וכן הלאה. אם אומנם כך הוא, קל להראות שעל כל עליה (שהיא בערך פי 3) יורדים בממוצע פי 4. כלומר בממוצע יורדים יותר מאשר עולים, כך שבסופו של דבר חייבים להגיע ל-1.
בעיה אחרת היא שהמספרים יכולים להיכנס למעגל – אין סיבה שאם נתחיל מן המספר 537 הסידרה לא תחזור בסופו של דבר ל-537 (בדיקה פשוטה מראה שהדבר לא קורה). אבל בהנחות דומות לאלה שהוזכרו, יש לכך סיכוי לא גדול, והסיכוי קטן והולך ככל שמתחילים ממספר גדול יותר. לכן רוב הסיכויים הם שההשערה נכונה.
האם ההשערה גם חשובה? הדבר תלוי בפתרון (אם בכלל יופיע אי פעם). אם אכן הפתרון יראה שהסדרה הזאת "מקרית" מבחינה זו שלאחר שני שלבים של "סולם" ו"חבל" יכול לבוא באותה הסתברות סולם כמו חבל, יהיה לכך ערך. בוודאי נבין משהו על הרכבם של מספרים.
תגבור כוחות במחלקה למתמטיקה ניסויית
אנה ליזהטוב
בסדרת כתבות קודמות ליווינו את ד"ר יסולא פז, מייסד ומנהל המחלקה למתמטיקה ניסויית בטכניון. יסולא הכניס לפקולטה למתמטיקה, ולטכניון בכלל, רוח חדשה ורעננה. בין הישגיו הגדולים היו חישוב בדרך ניסויית של ערכו המדויק (עד כדי דלתא) של האפסילון, פיתוח שיטה להיפוך מטריצות בעזרת מחוגה וסרגל, פתיחת המעבדות המתמטיות במרתפי בניין אמאדו ופיתוח שיטה חדשנית ללימוד המתמטיקה בשיטות של התניה באמצעות שכר ועונש מידיים.
כמו חדשנים גדולים לפניו, נתקל יסולא באטימותו של הממסד. שלטונות הטכניון מעכבים את קידומו האקדמי, ומונעים ממנו תקציבים שכה נחוצים למתמטיקאי ניסויי. אלא שלאחרונה מסתמן שינוי לטובה. אחרי מאבק של שנים, דומה שפעם אחת נוצחו צרות העין וחברתה, צרות האופקים. עד כה דומה היה שמלחמתו של ד"ר פז להשיג חבר סגל חדש היא מלחמת דון קישוט. אבל המאבק השקט נשא סוף-סוף פרי. למחלקה הגיע חבר חדש, אומנם עוזר מחקר ולא חבר סגל מן המניין, אבל בכל זאת כח מחקרי נוסף. שמו של החוקר החדש הוא שושן פנסה.
שושן, בחור גוץ, שחזותו הרדומה מסתירה נפש ערה, סיים לא מכבר את כתיבת עבודת הדוקטורט שלו במחלקה לפילוסופיה שימושית באוניברסיטת חיפה על הנושא "האם אפשר לחצות את גבולות הדעת?" (מסקנתו הייתה שלא.) אחר כך ויתר על הצעות עבודה ממחלקות יוקרתיות בחו"ל, כדי לעבוד במחיצתו של המדען הנערץ עליו. לבקשתנו, ניאותו ד"ר פז ו־ד"ר פנסה לספר לנו מעט על עבודתם המשותפת. ניכר שלשושן יש הרבה מה לספר, אך הוא עוצר בעד עצמו מפאת יראת הכבוד. בכל פעם שמוזכר שמו בפי הד"ר פז, עולה סומק קל בלחייו, בפרט כאשר האמור הוא דבר שבח. שכן, יסולא, המקמץ בדרך כלל במלים, לא חסך הפעם בדברי הלל.
במיוחד בירך ד"ר פז על הרוח החדשה שהכניס שושן לפקולטה למתמטיקה. "עולם המתמטיקה מצטיין בשמרנותו", אמר, "ויש לו הרבה ללמוד מן המנהגים האקדמיים בתחומים אחרים. למשל, שושן הנהיג בפקולטה את המנהג המועיל המקובל בפקולטה לפילוסופיה, שאחרי כל הרצאת אורח נערך דיון שבו מביע כל אחד את דעתו, ומסביר היכן, לדעתו, טעה המרצה."
מנהג חשוב נוסף שייבא ד"ר פנסה מעולם הפילוסופיה הוא להביא דברים בשם אומרם. פעמים רבות נלמדים בקורסים למתמטיקה משפטים ללא הזכרת שמו של ממציאם. מלבד אי הצדק האקדמי שבכך, גורם הדבר לזלזול מצד סטודנטים. כתוצאה מכך, נדרשות הוכחות למשפטים, שאחרת היו מתקבלים ללא עוררין. בקורסים לפילוסופיה מובאים משפטים תמיד בשם אומרם, וכשהאומר הוא פילוסוף חשוב, הדבר מבטיח כבוד לטענות. למשל, כאשר נאמר לסטודנט, שרנה דקארט אמר "אני חושב משמע אני קיים", או שויטגנשטין הוא שאמר שהעולם עשוי מעובדות לא מדברים, הוא מתייחס למשפטים בכובד הראש הראוי, בעוד שאחרת קרוב לודאי שהיה מבטלם כדברי הבל נוראיים. החל מן הסמסטר הבא יצוטטו משפטים מתמטיים בשם אומרם, וכך ייחסך מרבית הצורך בהוכחות (יוכחו רק משפטים שממציאיהם לא היו מתמטיקאים חשובים), והעומס על התלמידים יקטן בהרבה.
שושן מצידו, נראה כאילו עדיין אינו מאמין בזכות שנפלה בידיו, לעבוד במחיצתו של ד"ר פז. אף כי חדרו נמצא במרחק שתי דלתות ממשרדו של ד"ר פז, הוא מדבר כמעט בלחש, כאילו כדי לא להפריע את המדען הדגול מעבודתו. במיוחד הוא שמח לספר על אותו מחקר שעבורו זכו השניים לאחרונה בפרס יוקרתי - פרס הצלב האדום על פעילות הומניטרית למען מקופחי העולם.

"את הפרס קיבלנו על ספר חדש שכתבנו", מספר שושן. "שם הספר הוא 'ישויות נידחות במתמטיקה' והוא עוסק באובייקטים מתמטיים מקופחים. אני, מצדי, קיבלתי על עצמי בחפץ לב את תפקידו של נושא הכלים במלחמה צודקת זו.
"הכל התחיל", מספר שושן ועיניו בורקות, "כאשר ערב אחד דיברנו על תפקידיו של האלכסון הראשי במטריצה. כמובן היה זה בעיקר יסולא שדיבר, ואילו אני הקשבתי ורשמתי את דבריו. אתה יודע, אמר לי פתאום יסולא, אנשים שוכחים שלמטריצה יש שני אלכסונים. במה נגרע חלקו של האלכסון האחר?" מאותו רגע לא מצא לו יסולא מנוח. הוא חקר את תכונותיו של האלכסון הזה, מצא את המשפטים עליו, המקבילים למשפטים הידועים על האלכסון הראשי, ובמהרה היה בדפוס מאמר על האלכסון המקופח. אבל אז הבין יסולא שבמקום שבו נעשה עוול ליצור אחד יש לשער שקיימות עוולות נוספות. ואכן, לא היה צורך לטרוח הרבה כדי למצוא אובייקטים זנוחים כמעט לגמרי. אפילו בגאומטריה האלמנטרית מצא יסולא כאלה. למשל, כמה שיעורים מוקדשים בבית ספר התיכון לחוצה הזווית, לגובה ולתיכון, ולעומתם כמה שיעורים מוקדשים לחוצה הזווית בין הגובה לתיכון? או: מדוע נגרע חלקו של הלוגריתם על פי בסיס $latex {\pi}$? אף אחד כמעט שלא מזכיר אותו."
שושן הוא כיום האדם המקורב ביותר אל יסולא. אבל, אומר שושן, אין ביכולתו של איש לחלק עם מגלה גדול את בדידותו. אנשים כמו יסולא נושאים על גבם את צלב הקידמה המדעית. זוהי תמיד התמודדותו של אדם אחד. לפעמים צר לי עליו, כשאני יודע שהוא נשאר לילות שלמים במשרדו כדי לשרות עם המלאך. מה שביכולתי להציע לו הוא רק מעט עידוד ואת הערצתי. אל מלחמתו הוא יוצא אמיץ ובודד".
חידות לילדים
מאת קוונט - תרגום : אירנה גורליק
