חידות

לחידות המוצגות בגיליון זה יפורסמו רמזים בגיליון הבא ופתרונות מלאים בזה שלאחריו. נשמח לקבל את פתרונותיכם באמצעות המקום המיועד לכך בתחתית העמוד עד 24.12.2015 , אנא ציינו את שמכם, היישוב בו אתם גרים, שם ביה"ס שלכם והכיתה בה אתם לומדים. בגיליון הבא יפורסמו שמות הפותרים נכונה, וכן יובאו פתרונות יפים שייכתבו על ידכם.

חידה 1 –איך לחלק את העוגה המשולשת?

אורה ובני מחלקים ביניהם עוגה (שניתן להניח כי היא בגובה ומרקם אחיד, כך שכל אחד רוצה לקבל שטח גדול יותר של העוגה) לפי הכלל הבא: אורה בוחרת נקודה כלשהיא על גבי העוגה, ובני רשאי לחתוך את העוגה בקו ישר העובר דרך הנקודה שסימנה אורה אח"כ בני בוחר לעצמו את אחד החלקים והשני ניתן לאורה. בני ואורה בוחרים את מיקום הנקודה וכוון הקו כדי לקבל מקסימום משטח העוגה.

ברור שאם העוגה עגולה, הבחירה של אורה היא מרכז העיגול, וכל קו שיעביר בני יבטיח לו בדיוק חצי מהעוגה וגם אורה תקבל חצי עוגה.

החידה היא מה קורה כשלעוגה צורת משולש? מהי הנקודה הטובה ביותר שתבחר אורה? איך יעביר בני את קו החיתוך? בהנחה ששניהם עושים את הבחירות הטובות ביותר, איזה חלק מהעוגה יקבל בני ואיזה יישאר לאורה?

חידה 2–איך ליצור רבוע מרבוע ומשולש?

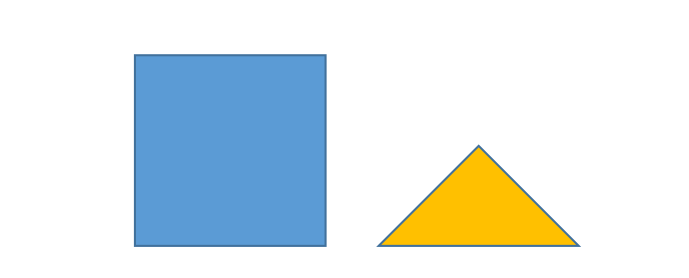
נתון ריבוע ומשולש ישר זווית ושווה שוקים הקטן בשטחו משטח הרבוע. איך ניתן לחתוך את הרבוע ל3 חלקים ע"י קוים ישרים, ואת המשולש ל2 חלקים ע"י קו ישר אחד, ומחמשת החלקים להרכיב ריבוע?

חידה 3– מה הדרך הקצרה של הנמלה לטיפת הדבש?

נתונה כוס זכוכית בעלת צורה גלילית, בקוטר 8 ס"מ ובגובה 8 ס"מ. על התחתית סמוך לדופן, בתוך הכוס, יש טיפת דבש. מחוץ לכוס, סמוך לתחתית, בנקודה המרוחקת ביותר מטיפת הדבש נמצאת נמלה. מה הדרך הקצרה ביותר של הנמלה לטיפת הדבש? מה אורכה?

רמזים לחידות מגיליון נובמבר 2015

חידה 1 – איך לחלק את המחרוזת?

חברו את המחרוזת בקצותיה ליצירת מעגל. השתמשו בשיטה דומה לזו של הוכחת המקרה החד ממדי של משפט בורסוק-אולם המופיע במאמרו של רון אהרוני בגיליון אוקטובר 2015.

חידה 2– איך למצוא את הדרך הנכונה?

יש למצוא דרך שהשאלה "תעבור" פעמיים דרך שני משיבים.

חידה 3– סידור אבני דומינו?

כמה פעמים מופיע כל מספר?

פתרון החידות גיליון אוקטובר 2015

חידה 1 –שמיכת טלאים

הפתרון לחידה – שימו לב לשלשה הפיתגוריאנית $latex 13^2 = 12^2 + 5^2$

אם היה אפשרי לפתור את החידה ע"י חלוקת הרבוע הגדול ל 3 חלקים בלבד, הרי שבחלק אחד תהינה 2 פינות של הרבוע הגדול שהמרחק (האנכי או האופקי) ביניהן הוא 13 בעוד ברבוע הנוצר לאחר החלוקה המרחק המקסימלי הוא 12. תנו דעתכם שבבעיה זו ניתן לסובב את החלקים החתוכים בכפולות של 90 מעלות בלבד.

את הפתרון ניתן להכליל לכל השלשות הפיתאגוריאניות מהצורה:

$latex \displaystyle (2m^2 + 2m)^2 + (2m+1)^2 = (2m^2 + 2m + 1)^2$

השרטוטים הבאים מתארים את חלוקת הרבוע הגדול והרכבת רבוע שאורך צלעו קטן ב 1 משלשה החלקים.

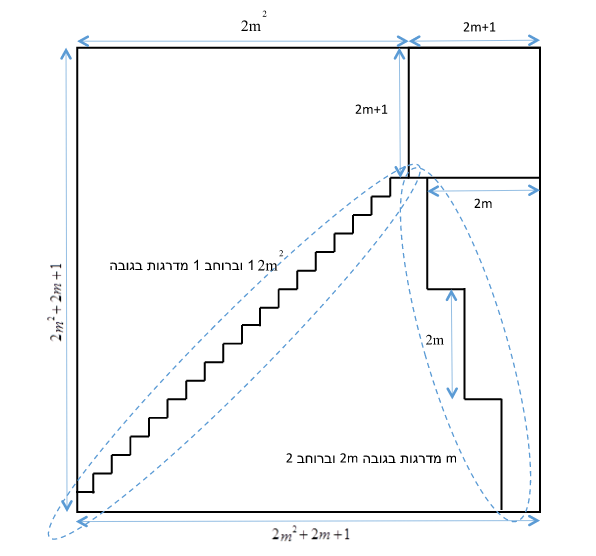
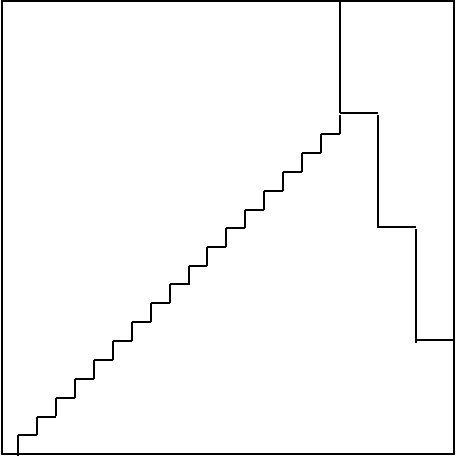
חידה 2–איזו ספרה חסרה?

נחשב את המספר מודולו 9.

קל לראות:

$latex 2^2 = 4 \pmod{9}$

$latex 2^4 = 7 \pmod{9}$

$latex 2^8 = 4 \pmod{9}$

$latex 2^{16} = 7 \pmod{9}$

מאחר ו: $latex 2^{29} = 2^{16} \cdot 2^8 \cdot 2^4 \cdot 2^1 = 7 \cdot 4 \cdot 7 \cdot 2 = 5 \pmod{9}$ ונתון שבתוצאה מופיעות כל הספרות פרט לאחת – הספרה החסרה היא 4 (סכום כל הספרות 1..9 הוא 0 מודולו 9).

חידה 3– איזה מספרים ניתן לרשום כסכום של רצף של מספרים טבעיים?

להלן פתרונו של עומר שמחי (בתיקונים קלים):

פתרון: כל מספר שאינו חזקה אי שלילית של 2.

הוכחה:   ראשית נשים לב כי אם מספר הוא סכום של רצף טבעיים (לפחות שניים) אזי הוא מהצורה:

$latex M = k + (k+1) + \dots + (k+n-1)$

כאשר $latex k$ הוא המספר הטבעי הראשון ועוד $latex n-1$ מספר החוברים ברצף.

קל לראות מסכום סדרה חשבונית ש:

$latex \displaystyle d = 1, a_1 = k \Rightarrow M = \frac{n \cdot (2k + 1 \cdot (n-1))}{2} = \frac{n \cdot (n + (2k-1))}{2}$

ראשית נראה כי כל מספר אי זוגי $latex M$ (שאינו 1 כמובן) ניתן להצגה כסכום רצף טבעיים:

$latex n=2 \Rightarrow M = 2k + 1, \forall k \in \mathbb{N}$ וזהו ביטוי לכל מספר אי זוגי גדול מאחד כמובן.

כעת נראה כי אם $latex M = 2^r, \forall r \in \mathbb{N} \cup \{0\}$ לא ניתן לבטא כסכום כנ"ל:

נשווה: $latex 2^r = \frac{n \cdot (n + 2k - 1)}{2}$

אולם אם $latex n (\gt 2)$ אי זוגי אזי נקבל סתירה כי אז לחזקה של 2 אמור להיות מחלק אי זוגי גדול מ1, ואם $latex n$ זוגי אזי $latex n + 2k-1$ אי זוגי ושוב סתירה מאותה סיבה.

לכן חזקה טבעית של 2 או המספר 1 לא ניתנים לייצוג כנ"ל.

כעת נותר להוכיח שכל זוגי שאינו חזקה של 2, דהיינו: $latex M = 2^r t, t \equiv 1 \pmod{2}, r \in \mathbb{N}$ ניתן להצגה.

כלומר, נחפש $latex n$ ו $latex k$ כך ש: $latex 2^r t = \frac{n \cdot (n + 2k - 1)}{2} \Leftrightarrow 2^{r+1} t = n \cdot (n + 2k - 1)$

כעת, נפריד לשני מקרים:

(1): $latex t \gt 2^{r+1}$:

נציב: $latex n = 2^{r+1} \Rightarrow t = n + 2k - 1 = 2^{r+1} + 2k - 1$

היות ש$latex k$ ניתן לבחירה חופשית, הרי שכל אי זוגי $latex t$ שמקיים את תנאי אי השיוויון כמובן יתקבל בצורה כזו.

(2): $latex t \lt 2^{r+1}$:

נבחר: $latex n = t \Rightarrow 2^{r+1} = n + 2k - 1= 2k + t -1 $

ושוב היות ש$latex t$ אי זוגי ו$latex k$ ניתן לבחירה חופשית נקבל שוב שאפשר לקבל כל חזקה של 2 שמקיימת את אי השוויון בצורה כזו בבחירה מתאימה של $latex k$.

מש״ל.

שמות הפותרים נכונה את החידות מגיליון נובמבר 2015

תומר שני, חניתה, בי"ס סולם צור כתה י"ב – כל החידות!